3.4: Isomers
- Page ID
- 225774
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This video gives a good overview of this topic. Before you begin reading this section, review section 1.5, which contains an introduction to isomerism.
Constitutional isomers
IUPAC defines constitutional isomerism as “isomerism between structures differing in constitution and described by different line formulae e.g. CH3OCH3 and CH3CH2OH.” Recall that there are three types of constitutional isomer commonly seen: Chain, positional and functional.
Isomers are molecules that have the same molecular formula, but have a different arrangement of the atoms in space. Consider butane:
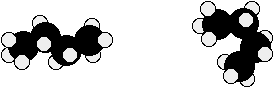
There are also endless other possible ways that this molecule could twist itself. There is almost completely free rotation around all the carbon-carbon single bonds. If you had a model of a molecule in front of you, you would have to take it to pieces and rebuild it if you wanted to make an isomer of that molecule. If you can make an apparently different molecule just by rotating single bonds, it’s not a constitutional isomer – it’s still the same molecule, just in a different “conformation” (see section 3.5. and 3.6.).
In constitutional isomerism, the atoms are arranged in a completely different order. This is easier to see with specific examples. What follows looks at some of the ways that structural isomers can arise. The names of the various forms of constitutional isomerism probably don’t matter all that much, but you must be aware of the different possibilities when you come to draw isomers.
Chain isomerism
These isomers arise because of the possibility of branching in carbon chains. For example, there are two isomers of butane, $$C_4H_{10}$$. In one of them, the carbon atoms lie in a “straight chain” whereas in the other the chain is branched.
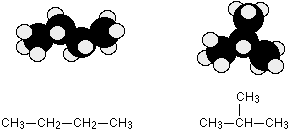
Be careful not to draw “false” isomers which are just twisted versions of the original molecule. For example, this structure is just the straight chain version of butane rotated about the central carbon-carbon bond.
You could easily see this with a model. This is the example we’ve already used at the top of this page.
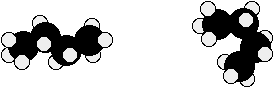
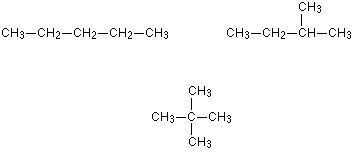
Example: Chain Isomers in Pentane
Pentane, C5H12, has three chain isomers. If you think you can find any others, they are simply twisted versions of the ones below. If in doubt make some models.
Position isomerism
In position isomerism, the basic carbon skeleton remains unchanged, but important groups are moved around on that skeleton.
Example: Positional Isomers in C5H12
For example, there are two structural isomers with the molecular formula C3H7Br. In one of them the bromine atom is on the end of the chain, whereas in the other it’s attached in the middle.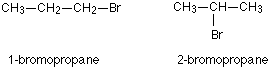
If you made a model, there is no way that you could twist one molecule to turn it into the other one. You would have to break the bromine off the end and re-attach it in the middle. At the same time, you would have to move a hydrogen from the middle to the end.
Another similar example occurs in alcohols such as $$C_4H_9OH$$
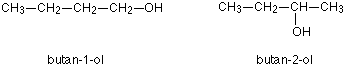
These are the only two possibilities provided you keep to a four carbon chain, but there is no reason why you should do that. You can easily have a mixture of chain isomerism and position isomerism – you aren’t restricted to one or the other.
So two other isomers of butanol are:
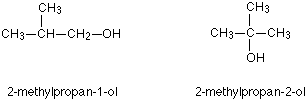
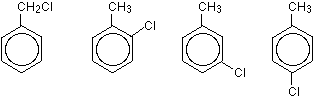
You can also get position isomers on benzene rings. Consider the molecular formula $$C_7H_7Cl$$. There are four different isomers you could make depending on the position of the chlorine atom. In one case it is attached to the side-group carbon atom, and then there are three other possible positions it could have around the ring – next to the $$CH_3$$ group, next-but-one to the $$CH_3$$ group, or opposite the $$CH_3$$ group.
Functional group isomerism
In this variety of constitutional isomerism, the isomers contain different functional groups – that is, they belong to different families of compounds (different homologous series).
Example: Isomers in C3H6O
A molecular formula $$C_3H_6O$$ could be either propanal (an aldehyde) or propanone (a ketone).

There are other possibilities as well for this same molecular formula – for example, you could have a carbon-carbon double bond (an alkene) and an -OH group (an alcohol) in the same molecule.
Another common example is illustrated by the molecular formula $$C_3H_6O_2$$. Amongst the several constitutional isomers of this are propanoic acid (a carboxylic acid) and methyl ethanoate (an ester).
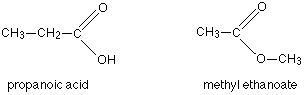
Contributors to the above section
Jim Clark (Chemguide.co.uk)
Stereoisomers
Stereoisomers are isomers that differ in the spatial arrangement of atoms, rather than the order of atomic connectivity. We gave a basic description in section 1.5, and stereoisomerism will be the main focus of chapter 4. However, one specific type of stereoisomer – geometric isomers – warrants further discussion as we begin looking in detail at hydrocarbon structures.
Geometric or cis-trans isomerism
We have defined isomers in a very general way as nonidentical molecules that possess the same number and kind of atoms. However, there are several ways in which isomers can be nonidentical. Among the alkenes, 1- and 2-butene are position isomers, because in these compounds the double bond has a different position in the carbon chain
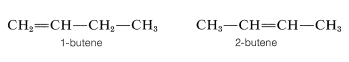
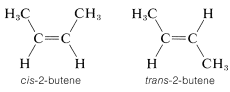
Most, but not all alkenes, have stereoisomers that are not identical because of different spatial arrangements of the component atoms. Thus there are two stereoisomers of 2-butene that differ in the geometric arrangement of the groups attached to the double bond. In one isomer, both methyl groups are on the same side of the double bond (cis-2-butene) and in the other, the methyl groups are on opposite sides of the double bond (trans-2-butene):
The two isomers clearly have the same structural framework but they differ in the arrangement of this framework in space – hence the designation stereoisomers. They owe their separate existence to the fact that the double bond is rigid and the parts of the molecule are not free to rotate with respect to each other about this bond. Therefore the isomers do not interconvert without breaking the double bond, and they exist as different compounds, each with its own chemical and physical properties. Ball-and-stick models of cis- and trans-2-butene are shown below, and the rigidity of the double bond is simulated in the model by a pair of stiff springs or bent sticks connecting the two carbons of the double bond.
It should be clear to you that there will be no cis-trans isomers of alkenes in which one end of the double bond carries identical groups. Thus we don not expect there to be cis-trans isomers of 1-butene or 2-methylpropene, and
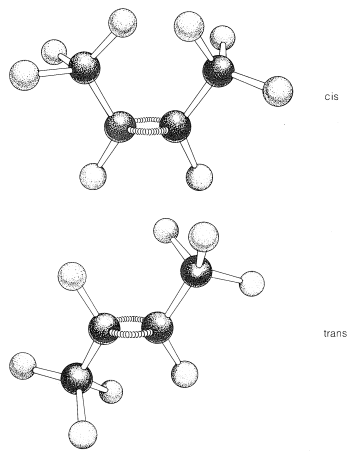
indeed none are known:

You may wish to verify this by making your own models of these substances.
Ring formation also confers rigidity on molecular structure such that rotation about the ring bonds is prevented. As a result, stereoisomerism of the cis-trans type is possible. For example, 1,2-dimethylcyclopropane exists in two forms that differ in the arrangement of the two methyl groups with respect to the ring.

Ball-and-stick models of cis and trans isomers of 1,2-dimethylcyclopropane
In the cis isomer, the methyl groups both are situated above (or below) the plane of the ring and in the trans isomer they are situated one above and one below, as shown in the figure. Interconversion of these isomers does not occur without breaking one or more chemical bonds.
Stereoisomers that do not interconvert rapidly under normal conditions, and therefore are stable enough to be separated, specifically are called configurational isomers. Thus cis– and trans-2-butene are configurational isomers, as are cis– and trans-1,2-dimethylcyclopropane. The terms cis-trans isomerism or geometric isomerism commonly are used to describe configurational isomerism in compounds with double bonds and rings. When referring to the configuration of a particular isomer, we mean to specify its geometry. For instance, the isomer of 1,2-dichloroethene shown below has the trans configuration; the isomer of 1,3-dichlorocyclobutane has the cis configuration:

Cis-trans isomerism is encountered very frequently. By one convention, the configuration of a complex alkene is taken to correspond to the configuration of the longest continuous chain as it passes through the double bond. Thus the following compound is trans-4-ethyl-3-methyl-3-heptene, despite the fact that two identical groups are cis with respect to each other, because the longest continuous chain is trans as it passes through the double bond:
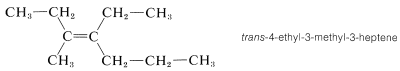
Notice that cis-trans isomerism is not possible at a carbon-carbon triple bond, as for 2-butyne, because the bonding arrangement at the triply bonded carbons is linear:

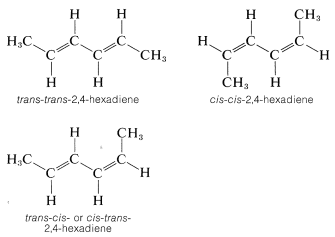
Many compounds have more than one double bond and each may have the potential for the cis or trans arrangement. For example, 2,4-hexadiene has three different configurations, which are designated as trans-trans, cis-cis, and trans-cis. Because the two ends of this molecule are identically substituted, the trans-cis becomes identical with cis-trans:
The importance of drawing geometric isomers properly
It’s very easy to miss geometric isomers in exams if you take short-cuts in drawing the structural formulae. For example, it is very tempting to draw but-2-ene as
CH3CH=CHCH3
If you write it like this, you will almost certainly miss the fact that there are geometric isomers. If there is even the slightest hint in a question that isomers might be involved, always draw compounds containing carbon-carbon double bonds showing the correct bond angles (120°) around the carbon atoms at the ends of the bond. In other words, use the format shown in the last diagrams above.
How to recognize the possibility of geometric isomerism
You obviously need to have restricted rotation somewhere in the molecule. Compounds containing a carbon-carbon double bond have this restricted rotation as do compounds with multiple groups attached to a ring, so you need to consider the possibility of geometric isomers. Think about this case with a C=C double bond:
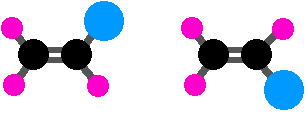
Although we’ve swapped the right-hand groups around, these are still the same molecule. To get from one to the other, all you would have to do is to turn the whole model over. You won’t have geometric isomers if there are two groups the same on one end of the bond – in this case, the two pink groups on the left-hand end. So there must be two different groups on the left-hand carbon and two different groups on the right-hand one. The cases we’ve been exploring earlier are like this:

But you could make things even more different and still have geometric isomers:
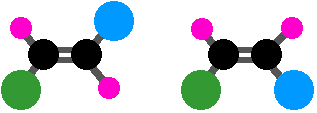
Here, the blue and green groups are either on the same side of the bond or the opposite side. Or you could make everything different. You still get geometric isomers, but by now the words cis and trans are meaningless. This is where the more sophisticated E-Z notation comes in, and this will be covered soon in section 4.3..
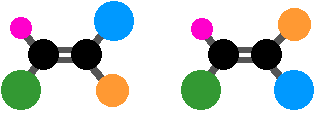
Summary
To get geometric isomers you must have:
- restricted rotation (often involving a carbon-carbon double bond for introductory purposes);
- two different groups on the left-hand end of the bond and two different groups on the right-hand end. It doesn’t matter whether the left-hand groups are the same as the right-hand ones or not.
Conformational isomers
Example: Ethane (CH3CH3)
Due to free rotation around the carbon-carbon bond, the ethane molecule could assume an infinite number of conformations, two of which are shown below as “saw-horse formulae”:

Further Reading
Khan Academy
| Web Pages | Videos | Tutorial | Practice Problems |
Information on isomers | Isomers video
| Drawing isomers
| Isomer quiz
|
Difference between Isomers and resonance structures | Isomers video
| Isomer quiz
| |
Lewis formulae, structural isomerism, resonance | |||
| Structural isomerism
|
- 5.1: Isomers. Authored by: Allison Soult, Ph.D. (Department of Chemistry, University of Kentucky) and CK-12 Foundation by Sharon Bewick, Richard Parsons, Therese Forsythe, Shonna Robinson, and Jean Dupon.. Provided by: University of Kentucky. Located at: https://chem.libretexts.org/LibreTexts/University_of_Kentucky/UK%3A_CHE_103_-_Chemistry_for_Allied_Health_(Soult)/Chapters/Chapter_5%3A_Properties_of_Compounds/5.1%3A_Isomers. Project: Chemistry LibreTexts. License: CC BY-NC-SA: Attribution-NonCommercial-ShareAlike