13.6: Aromaticity

Aromaticity is a property of conjugated cycloalkenes in which the stabilization of the molecule is enhanced due to the ability of the electrons in the $$\pi$$ orbitals to delocalize. This act as a framework to create a planar molecule.

Introduction

Why do we care if a compound is aromatic or not? Because we encounter aromatics every single day of our lives. Without aromatic compounds, we would not only be lacking many material necessities, our bodies would also not be able to function. Aromatic compounds are essential in industry; about 35 million tons of aromatic compounds are produced in the world every year to produce important chemicals and polymers, such as polyester and nylon. Aromatic compounds are also vital to the biochemistry of all living things. Three of the twenty amino acids used to form proteins (“the building blocks of life”) are aromatic compounds and all five of the nucleotides that make up DNA and RNA sequences are all aromatic compounds. Needless to say, aromatic compounds are vital to us in many aspects.

The three general requirements for a compound to be aromatic are:

1. The compound must be cyclic
2. Each element within the ring must have a p-orbital that is perpendicular to the ring, hence the molecule is planar.  This means that the ring cannot contain a neutral sp³ carbon.
3. The compound must follow Hückel’s Rule (the ring has to contain 4n+2 p-orbital electrons).

Among the many distinctive features of benzene, its aromaticity is the major contributor to why it is so unreactive. This section will try to clarify the theory of aromaticity and why aromaticity gives unique qualities that make these conjugated alkenes inert to compounds such as Br₂ and even hydrochloric acid. It will also go into detail about the unusually large resonance energy due to the six conjugated carbons of benzene.

The delocalization of the p-orbital carbons on the sp² hybridized carbons is what gives the aromatic qualities of benzene.

Basic Structure of Benzene

Because of the aromaticity of benzene, the resulting molecule is planar in shape with each C-C bond being 1.39 Å in length and each bond angle being 120°. You might ask yourselves how it’s possible to have all of the bonds to be the same length if the ring is conjugated with both single (1.47 Å) and double (1.34 Å), but it is important to note that there are no distinct single or double bonds within the benzene. Rather, the delocalization of the ring makes each count as one and a half bonds between the carbons which makes sense because experimentally we find that the actual bond length is somewhere in between a single and double bond. Finally, there are a total of six p-orbital electrons that form the stabilizing electron clouds above and below the aromatic ring.

Evidence of aromaticity: Heats of hydrogenation

One of the ways to test the relative amounts of resonance energy in a molecule is to compare the heats of hydrogenation between similar compounds. For instance, if we compare cyclohexene, 1,3-cyclohexadiene, and benzene, we would expect that their heats of hydrogenation will increase since the number of double bonds increases respectively. However, experimental evidence suggests that the actual heat of hydrogenation for benzene is actually 49.3 kcal/mole, making it even more stable than the 1,3-cyclohexadiene even though it has two double bonds, compared to benzene’s three double bonds. This characteristic can be attributed to the aromaticity of benzene which delocalizes the electrons of the six pi orbitals.

 

References

1. P. Schleyer, “Aromaticity (Editorial)”, Chemical Reviews, 2001.
2. P. Schleyer, “Introduction: Delocalization-? and ? (Editorial)”, Chemical Reviews,  2005.
3. Vollhardt, K. Peter C., and Neil E. Schore. Organic Chemistry: Structure and Function. New York: W.H. Freeman and Company, 2007.

Exercises

1. What is the hybridization of each carbon and the overall shape of benzene?
2. What is the resonance energy of benzene?
3. Place the following compounds in order of heats of hydrogenation from smallest to greatest : Benzene, 1,3-Cyclohexadiene, and Cyclohexene.

 

Answers

[reveal-answer q=”378415″]Show Answer[/reveal-answer]
[hidden-answer a=”378415″]

1. All six carbons are sp2  hybridized and the aromaticity of the benzene creates a planar molecule.
2. 29.6 kcal/mol
3. Cyclohexene < Benzene < 1,3-Cyclohexadiene.[/hidden-answer]

What makes a structure aromatic?

Valence bond theory uses Lewis diagrams to depict structure and bonding of covalent entities, such as molecules and polyatomic ions, henceforth referred to just as molecules. The Lewis diagram of many a molecule, however, is not consistent with the observed properties of the molecule.  The Lewis diagram of some molecules suggests a ring bearing a fully conjugated $$\pi$$-electron system, or loop of $$\pi$$ electrons, provided each atom in the ring is sp²– or sp-hybridized.  Note that in cases like 5 that contain sp3 atoms with lone pairs, these atoms (usually N, O or S) can rehybridize to sp² and make the remaining p-orbital available for bonding.  A fully bonded sp³ carbon cannot do this, and thus cannot form part of a fully conjugated system.

• cyclobutadiene (1)

• benzene (2)

• cyclooctatetraene (3)

• pyridine (4)

• pyrrole (5)

• cyclopentadienyl cation (6)

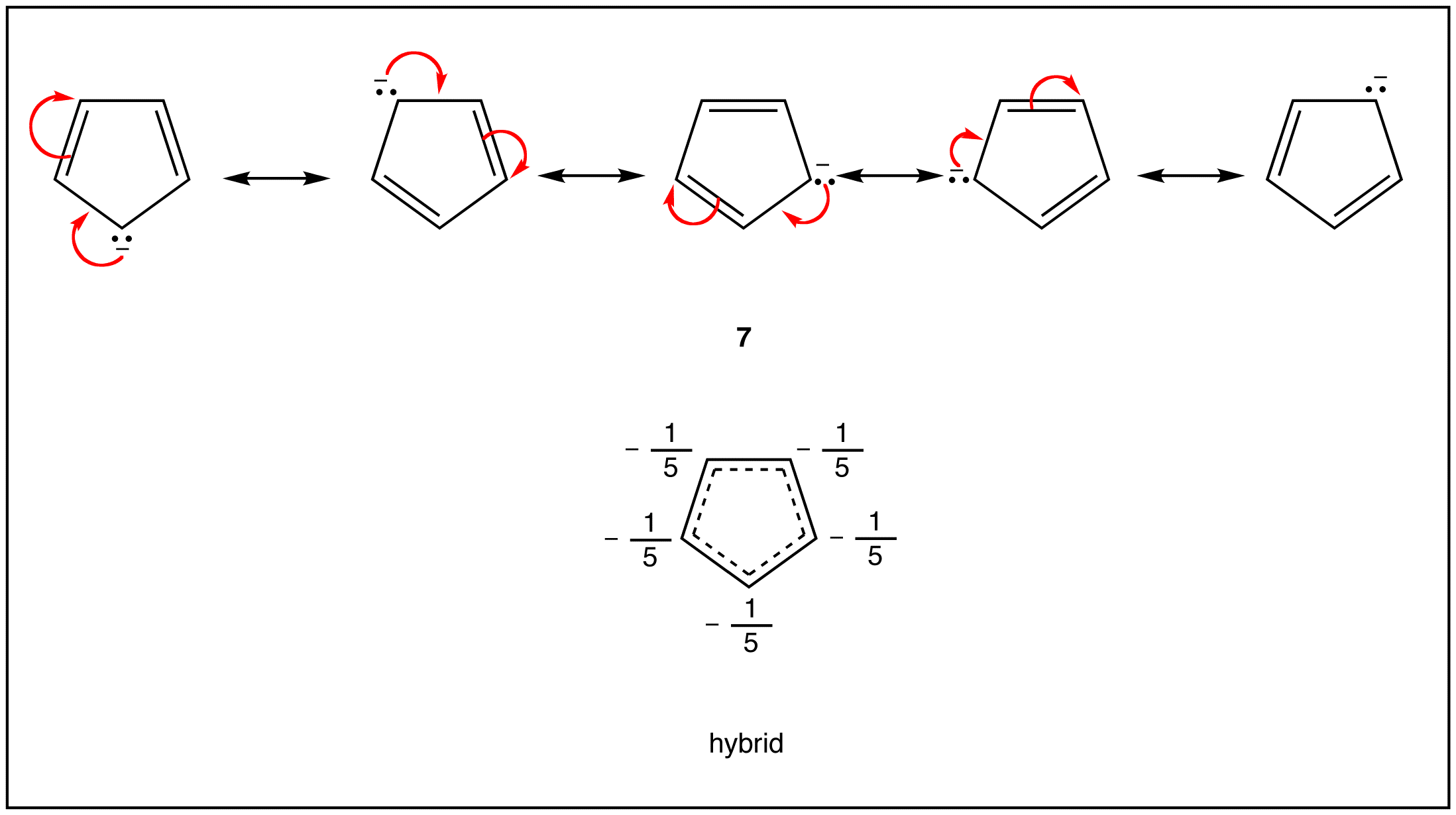
• cyclopentadienyl anion (7)

As evident from the stability of $$\pi$$ electrons however, only some such rings actually have a loop of $$\pi$$ electrons. Of the above examples, only the rings in 2, 4, 5, and 7 have a loop of $$\pi$$ electrons. Resonance theory can predict that the rings in 2, 4, 5, and 7 have a loop of $$\pi$$ electrons.

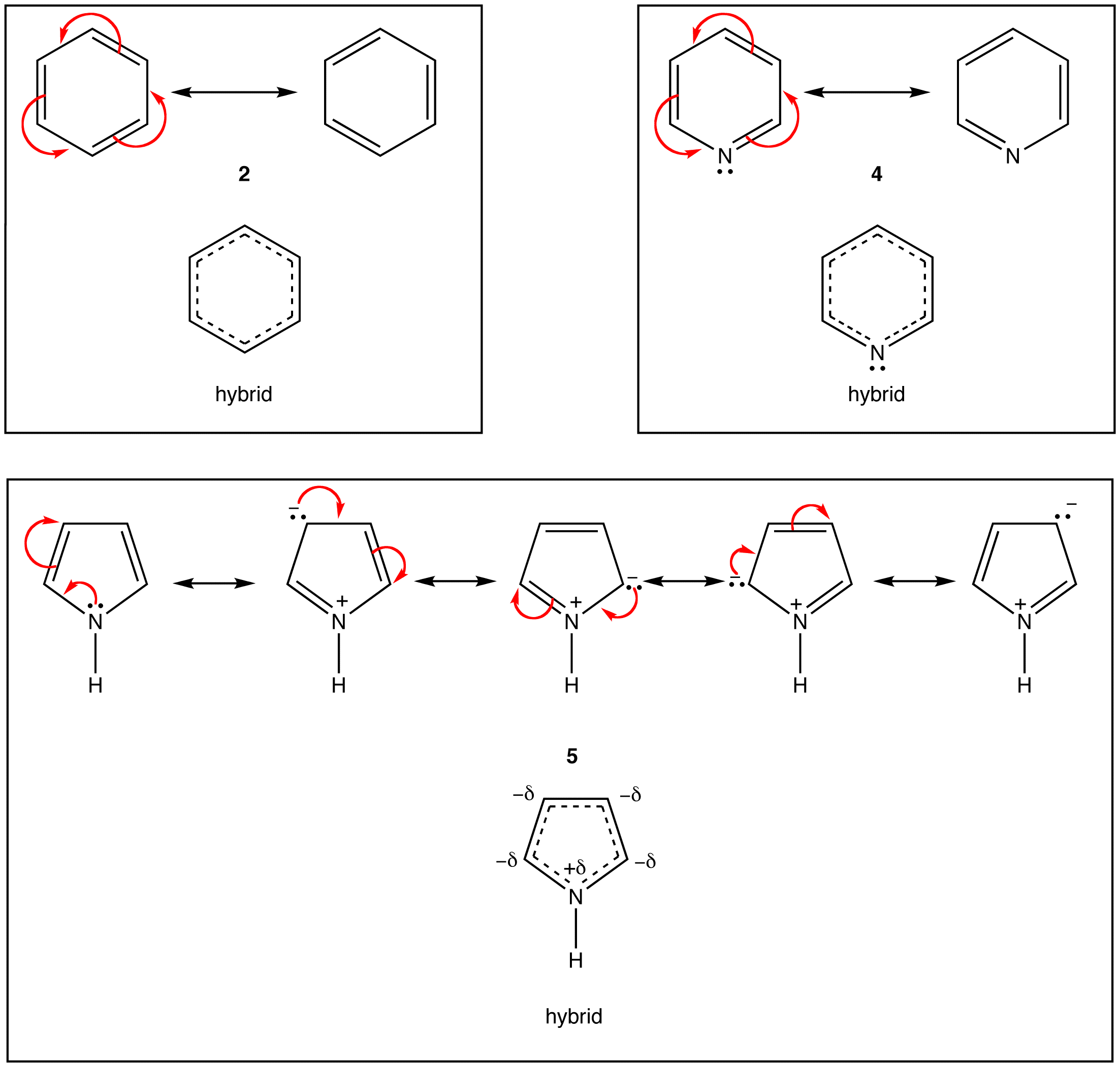
According to resonance theory, however, the rings in 1, 3, and 6 also should have a loop of $$\pi$$ electrons.

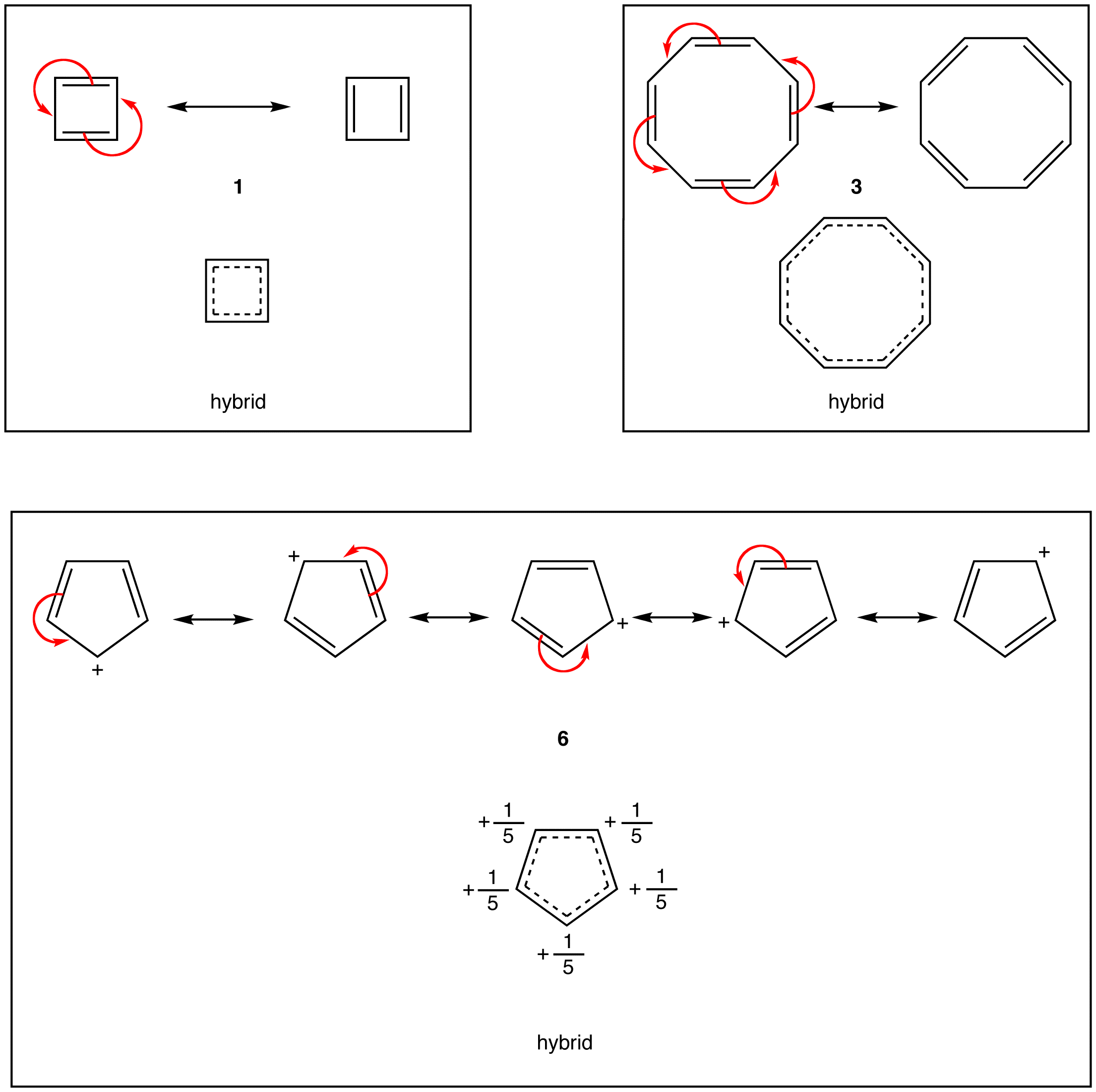
Evidently, resonance theory is no more reliable a tool than Lewis diagrams to be used in predicting if a ring has a loop of $$\pi$$ electrons. Rings whose Lewis diagram implies a loop of $$\pi$$ electrons can be classified into three classes:

1. aromatic rings
2. antiaromatic rings
3. nonaromatic rings

To find whether a ring is aromatic, antiaromatic, nonaromatic, or none of the above, use the following flow chart.

Flowchart for determining aromatic behavior in cyclic molecules.

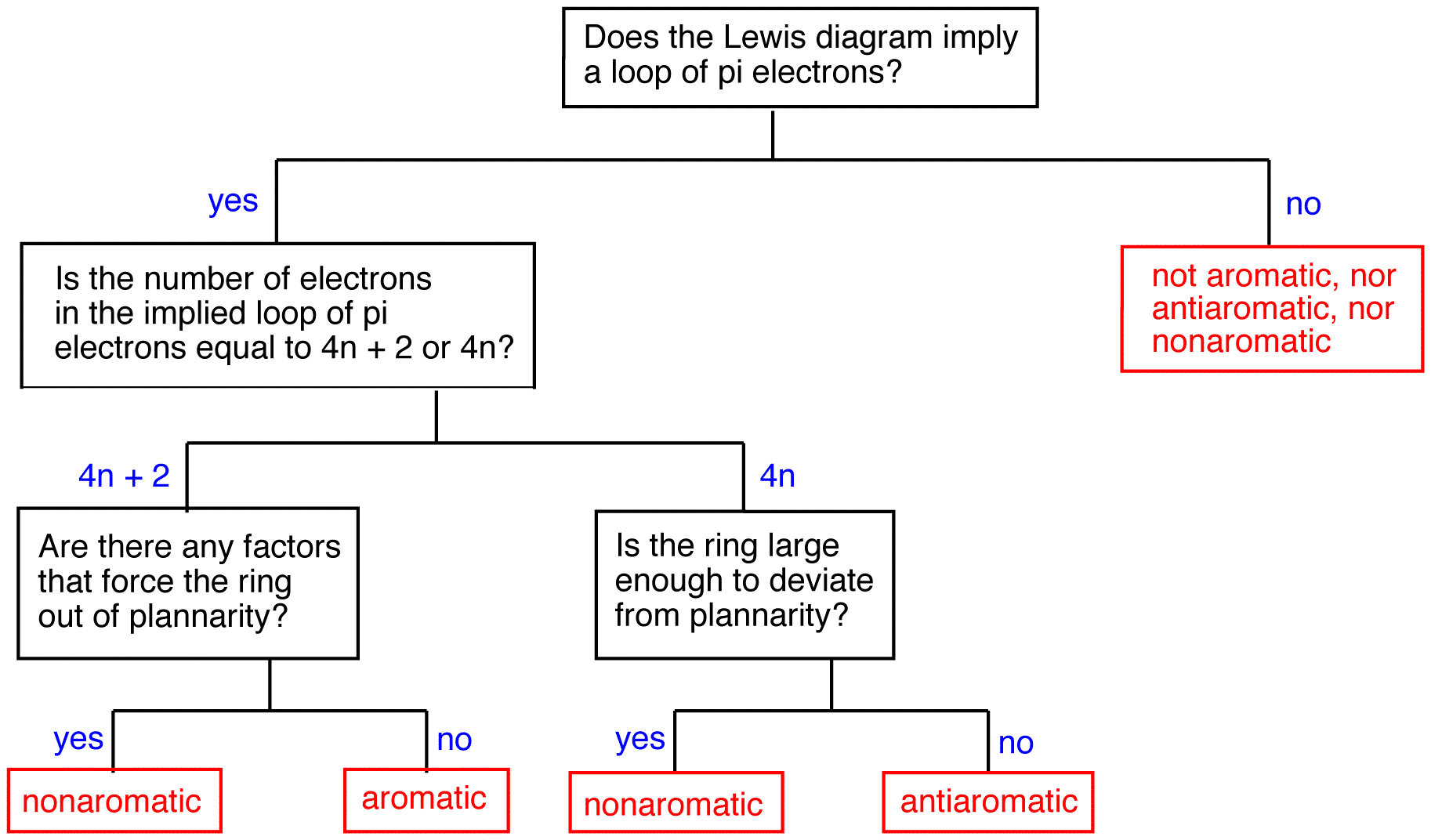
Aromatic rings

A ring that does have a loop of $$\pi$$ electrons is said to be aromatic. Thus, the rings in 2, 4, 5, and 7 are aromatic. A compound whose molecule contains one or more aromatic rings is called an aromatic compound. Thus, 2, 4, 5, and 7 are aromatic compounds. There are chemical and spectroscopic methods that can be used to experimentally determine whether a ring is aromatic or not. All aromatic rings share two structural features:

1.  The ring is planar.
2. The ring obeys the Hückel’s rule, which states that the number of electrons in the loop of $$\pi$$ electrons is equal to 4n + 2, where n is zero or a positive whole number.

 

As is evident from the above examples, determining whether a ring obeys the Hückel’s rule or not using the Lewis diagram is straightforward.  However, determining whether a ring is planar or not requires careful consideration of many factors. A case in point is [10]annulene (10).

If the ring in 10, which obeys the Hückel’s Rule, were planar, the hydrogen atoms on C-2 and C-7, which are inside the ring, would have to occupy the same space, which would be physically impossible.  To accommodate the hydrogen atoms on C-2 and C-7 inside the ring, the ring is forced to deviate from planarity. Thus, 10 is not aromatic. If [10]annulene were to assume a configuration in which all double bonds were cis double bonds (11), the ring would be planar and, therefore, be aromatic.

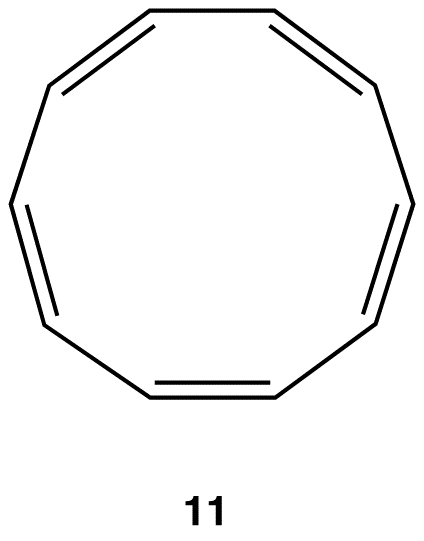
Experimentally, however, [10]annulene exists exclusively as 10, indicating that the stability gained by having a loop of $$\pi$$ electrons in 11 is outweighed by considerable angle strain.

Antiaromatic rings

A ring that does not have a loop of $$\pi$$ electrons and is extremely unstable is said to be antiaromatic. A compound whose molecule contains one or more antiaromatic rings is called an antiaromatic compound.  The rings in 1 and 6 are antiaromatic. 1 can be isolated only in an inert, solid matrix (helium, argon, etc.) at temperatures approaching absolute zero.  Under all other conditions, it dimerizes rapidly.

Experiments have shown that the ring in 1 is not a square but a rectangle, which is evidence that the ring in 1 does not have a loop of $$\pi$$ electrons. According to molecular orbital theory, 1 is a diradical, which is consistent with its extreme reactivity. 6 has never been observed.

All antiaromatic rings share two features:

1. The ring is planar.
2. If the ring had a loop of $$\pi$$ electrons as implied by the Lewis diagram, the number of electrons in the loop would be equal to 4n, where n is zero or a positive whole number.

Large and, therefore, flexible rings whose Lewis structure suggests a loop of $$\pi$$ electrons containing 4n number of electrons avoid being antiaromatic by deviating from planarity.

e.g.:

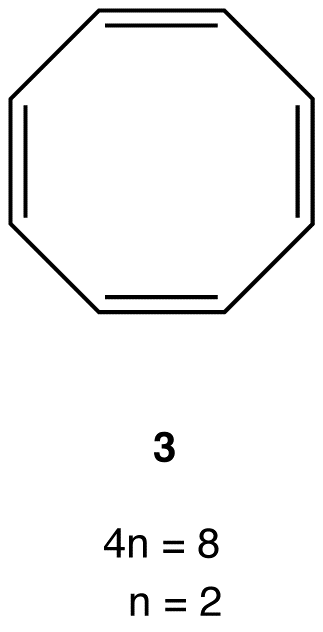
Experimentally, 3 is about as stable as any typical alkene, meaning 3 is not antiaromatic. There are no antiaromatic rings containing more than five atoms in the ring.

Nonaromatic rings

A ring that does not have a loop of $$\pi$$ electrons but is not antiaromatic is said to be nonaromatic. A compound whose molecule contains one of more nonaromatic rings is called a nonaromatic compound. A ring whose $$\pi$$ system contains a 4n number of electrons but avoids being antiaromatic by deviating from planarity is nonaromatic. For example,

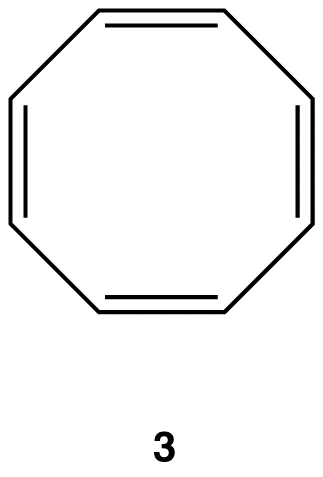
Experimentally, 3 exists in the following nonplanar conformation, known as the tub conformation, in which no two adjacent double bonds are on the same plane. Thus, there is no loop of $$\pi$$ electrons in the ring in 3; 3 is nonaromatic.

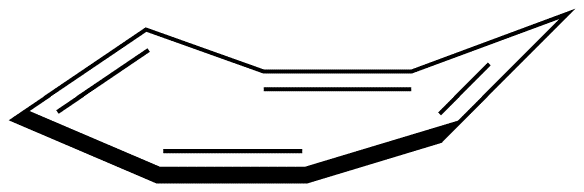
A ring whose $$\pi$$ system contains 4n + 2 number of electrons, but is forced to deviate from planarity is also nonaromatic. This is why [10]annulene (10) is nonaromatic.

see also annulene, heteroaromatic compound

13.4.4. A closer examination of Huckel’s Rule and the Polygon Rule

Cyclobutadiene and Cyclooctatetraene

More than 100 years ago, Kekule recognized the possible existence of other conjugated cyclic polyalkenes, which at least superficially would be expected to have properties like benzene. The most interesting of these are cyclobutadiene, $$23$$, and cyclooctatetraene, $$24$$:

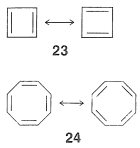
For each we can write two equivalent planar VB structures, and the qualitative VB method would suggest that both compounds, like benzene, have substantial electron-delocalization energies. However, the planar structures would have abnormal $$\ce{C-C=C}$$ angles, and consequently at least some degree of destabilization associated with these bond angles (Section 12-7). Nonetheless, estimation of the strain energies show that while they are substantial, they are not prohibitive. Should then these molecules be stabilized by resonance in the same sense as benzene is postulated to be?

In 1911 a German chemist, R. Willstatter (Nobel Prize 1915), reported an extraordinary thirteen-step synthesis of cyclooctatetraene from a rare alkaloid called pseudopelletierine isolated from the bark of pomegranate trees. The product was reported to be a light-yellow, highly unsaturated compound that absorbed four moles of hydrogen to form cyclooctane. Numerous tries to repeat the Willstatter synthesis were unsuccessful, and in the 1930s the prevailing opinion was that the product had been misidentified. However, during the Second World War, the German chemist W. Reppe found that cyclooctatetraene can be made in reasonable yields by the tetramerization of ethyne under the influence of a nickel cyanide catalyst:

The properties of the product substantiated Willstatter’s reports and it became clear that cyclooctatetraene is not like benzene.

Subsequent studies of the geometry of the molecule revealed further that it is nonplanar, with alternating single and double bonds, $$25a$$:

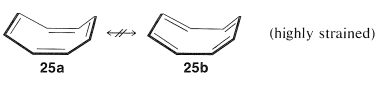
This geometry precludes the possibility of two equivalent VB structures, as for benzene, because, as you will see if you try to make a ball-and-stick model, $$25b$$ is highly strained and not energetically equivalent to $$25a$$ at all. Thus we can conclude that the delocalization energy of cyclooctatetraene is not large enough to overcome the angle strain that would develop if the molecule were to become planar and allow the $$\pi$$ electrons to form equivalent $$\pi$$ bonds between all of the pairs of adjacent carbons.

Cyclobutadiene, $$23$$, eluded Kekule, Willstatter, and a host of other investigators for almost 100 years. As more work was done, it became increasingly clear that the molecule, when formed in reactions, was immediately converted to something else. Finally, the will-o’-the-wisp was captured in an essentially rigid matrix of argon at $$8 \: \text{K}$$. It was characterized by its spectral properties (not by combustion analysis). On warming to even $$35 \: \text{K}$$, it dimerizes to yield $$26$$:

One possibility for the lack of stability$$^4$$ of cyclobutadiene is that the angle strain associated with having four $$sp^2$$ carbons in a four-membered ring is much greater than estimated. However, the stable existence of many compounds with four such $$sp^2$$ carbons, for example $$27$$ and $$28$$, make this argument weak, if not invalid:

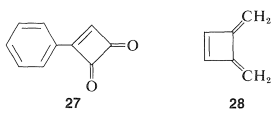
Why, then, is cyclobutadiene so unstable and reactive? On this point, and also with respect to the nonaromatic character of cyclooctatetraene, the simple qualitative VB method that we have outlined is no help whatsoever. There is no way simply to look at the electron-pairing schemes $$23$$ and $$24$$ and see any difference between them and the corresponding schemes for benzene.$$^5$$

It is in this area that qualitative MO procedures have great success because there are general characteristics of the $$\pi$$ molecular orbitals of monocyclic, conjugated polyene systems that predict differences in the properties of cyclobutadiene, benzene, cyclooctatetraene, and other similar compounds that are not obvious from the simple VB method.

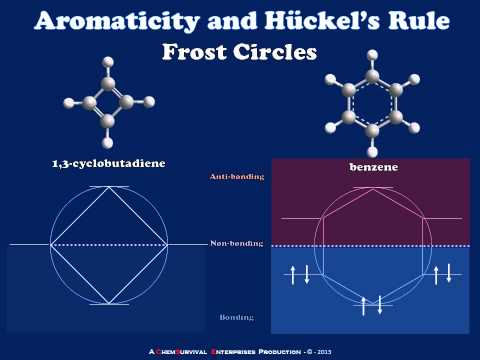
As a rule, for $$N$$ parallel atomic $$p$$ orbitals overlapping in the $$\pi$$ manner in a monocyclic array, there will be just one lowest molecular orbital, with all the atomic orbitals having the same phase. This will be seen for benzene in Figure 21-5. What is harder to understand without going through the calculations is that the higher-energy molecular orbitals for cyclic conjugated polyenes are predicted to come in successive degenerate$$^6$$ pairs, as shown in Figure 21-13 for $$N = 3$$ to $$9$$.

Figure 13.7: Calculated molecular-orbital energies of planar cyclic $$\pi$$-orbital systems made up of $$N$$ $$2p$$ carbon atomic orbitals, in units of $$\alpha$$ and $$\beta$$.

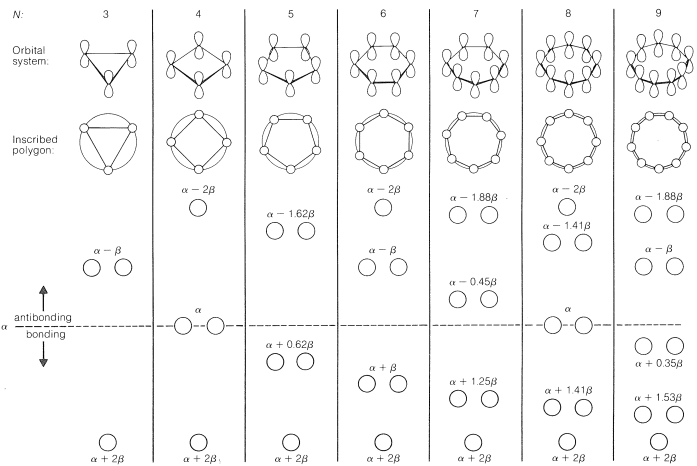
The qualitative ordering and, indeed, the numerical values of the energies of the $$\pi$$ molecular orbitals for a cyclic system of $$N$$ $$p$$ orbitals can be derived in a very simple way. It is necessary only to inscribe a regular polygon with $$N$$ sides inside a circle of radius $$2 \beta$$ with a corner down. For example, for $$N = 5$$ we get the following:

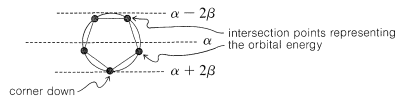
The molecular orbital energies are in units of $$\beta$$ at the corners of the polygon. The nonbonding level corresponds to the horizontal dashed line drawn through the center of the circle.

The data of Figure 13.7. provide a rationale for the instability of cyclobutadiene and cyclooctatetraene. For cyclobutadiene, we can calculate that four $$\pi$$ electrons in the lowest orbitals will lead to a predicted $$\pi$$-electron energy of $$2 \left( \alpha + 2 \beta \right) + 2 \left( \alpha \right) = 4 \alpha + 4 \beta$$, which is just the $$\pi$$-electron energy calculated for two ethene bonds. The delocalization energy of the $$\pi$$ electrons of cyclobutadiene therefore is predicted to be zero!

Another feature of the $$\pi$$ system of cyclobutadiene is that the four $$\pi$$ electrons do not suffice to fill the three lowest orbitals and, if we apply Hund’s rule, the best way to arrange the electrons is as in $$29$$, with two unpaired electrons, which is known as a triplet state:$$^7$$

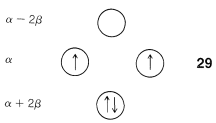
With the MO predictions of zero delocalization energy and an electronic configuration with unpaired electrons, we should not be surprised that cyclobutadiene readily dimerizes to give $$26$$ even at very low temperatures.

The energies of the molecular orbitals calculated for planar cyclooctatetraene (Figure 13.7.) lead to a predicted delocalization energy of $$\left( 8 \alpha + 9.64 \beta \right) – \left( 8 \alpha + 8 \beta \right) = 1.64 \beta$$ $$\left( \sim 31 \: \text{kcal} \right)$$, which is smaller than that of benzene, even though there are eight atomic orbitals instead of six through which the electrons are delocalized. Furthermore, the lowest electronic configuration for the planar molecule is, like cyclobutadiene, predicted to be a triplet. Experimental evidence indicates that the positions of the double bonds of cyclooctatetraene shift slowly as the result of formation of the molecule in the unstable planar state. The energy input required to flatten the molecule is about $$15 \: \text{kcal mol}^{-1}$$:

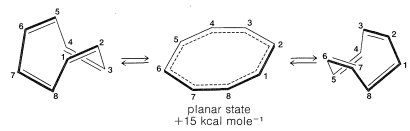
Because the bonding molecular orbitals for $$\pi$$ systems such as in Figure 13.7. will be just filled with 2, 6, or 10 electrons to give singlet states, and 4 or 8 electrons would give triplet states, a $$\left( 4n + 2 \right)$$ $$\pi$$-electron rule was formulated for stable configurations and a $$4n$$ $$\pi$$-electron rule for unstable configurations, where $$n$$ is an integer. Thus 2, 6, 10, 14, $$\cdots$$ $$\pi$$ electrons will be favorable and 4, 8, 12 $$\cdots$$ $$\pi$$ electrons will be unfavorable. This rule is the work of the German theoretician, E. Huckel, who devised the simple form of molecular orbital theory we have described in this chapter. The theory is appropriately called Huckel MO theory, and the rule is Huckel’s $$4n + 2$$ rule.

As Huckel formulated, the $$4n + 2$$ rule applies only to monocyclic systems. However, as a practical matter it can be used to predict the properties of polycyclic conjugated polyenes, provided the important VB structures involve only the perimeter double bonds, as in the following examples:

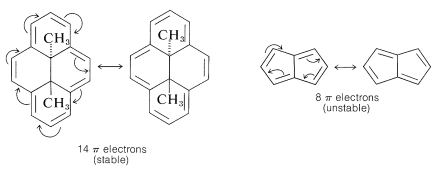
Application of the $$4n + 2$$ rule to other $$\pi$$ systems, such as $$30$$ and $$31$$, is not valid because good VB structures cannot be written that involve changes in the pairing schemes of the perimeter electrons all at once.

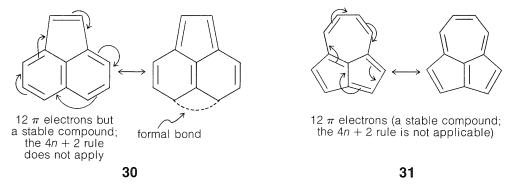
Application of Resonance and of the $$4n + 2$$ Rule to Cyclic Ions

The hydrogens of the $$\ce{-CH_2}-$$ group of 1,3-cyclopentadiene are acidic. In fact, they are considerably more acidic than the ethyne hydrogens of the 1-alkynes. This means that 1,3-cyclopentadiene is at least $$10^{30}$$ times more acidic than the ordinary alkanes. The reason is that loss of one of the $$\ce{CH_2}$$ protons of cyclopentadiene results in formation of an especially stabilized anion:

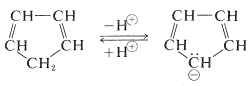
The structure of the anion may be described as a hybrid of five energetically equivalent structures, $$34a$$ through (34e). The unshared electron pair therefore is delocalized over five carbon atoms, and the resulting delocalized anion is much more stable than expected for any one of the equivalent localized structures:

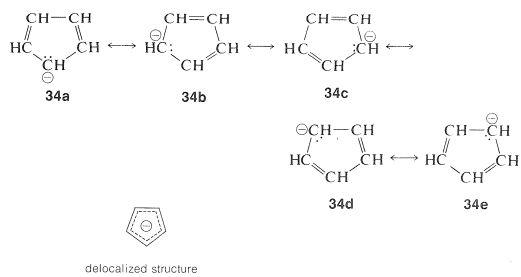
This looks very reasonable, although the simple beauty is seemingly destroyed by the fact that the cyclopentadienyl cation is not very stable, despite the five structures, $$35a$$ through $$35e$$, that may be written for it:

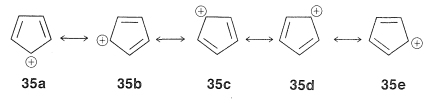
The experimental evidence is clear that, not only is the cation not stabilized in the same way as the anion, it also has a triplet electronic configuration. These facts agree with the molecular orbitals of Figure 21-13 for a cyclic system with five $$p$$ orbitals, and also with the $$4n + 2$$ rule, because $$34$$ has six $$\pi$$ electrons, whereas $$35$$ has only four.

Extension of these ideas to the other ring sizes of Figure 21-13 suggests that all of the following ions, which have $$\left( 4n + 2 \right)$$ $$\pi$$ electrons, should be unusually stable:

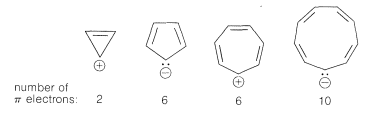
In contrast, the following should be unstable with $$4n$$ $$\pi$$ electrons and triplet electronic configurations:

These predictions indeed are borne out by many experiments, some of which we will discuss later.

$$^4$$It should be recognized that the term “stability” is subject to many interpretations. One criterion of stability would be whether an isolated molecule would fragment spontaneously in interstellar space, such as one would expect for a “molecule” consisting of two neon atoms $$1.5 \: \text{Å}$$ apart (see Figure 4-6). A different criterion would be whether a molecule could be preserved in the presence of the same or other kinds of molecules at some specified temperature. The classical criterion would be whether the substance could be isolated, put into a bottle and preserved for at least a short time. All of the existing evidence indicates that cyclobutadiene molecules would not spontaneously decompose in interstellar space, but they do react with each other extremely readily, even at low temperatures, and can be preserved only by being held isolated from one another in a rigid matrix of a very inert material, such as solid argon. “Stability” in the sense of “lack of reactivity” has to be carefully defined in terms of experimental conditions. For example,  is very unstable in the presence of nucleophiles such as water or methanol, whereas it is quite stable in “super-acid solutions” where no good nucleophiles are present (Section 10-3B).

$$^5$$A rather simple extension of the VB method by what is called the “orbital-phase continuity principle” does permit the qualitative judgment that cyclobutadiene should be less stable than benzene [see W. A. Goddard III, J. Amer. Chem. Soc. 94, 743 (1972), for applications to many processes for which VB theory generally has been regarded as incapable of giving much insight].

$$^6$$Degenerate orbitals have the same energy; see this page in Libretexts.

$$^7$$The name “triplet state” is used because a system with two unpaired electrons has three different energy states in a magnetic field.

A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/ochem2walker/?p=62

Contributors

• Gamini Gunawardena from the OChemPal site (Utah Valley University)
• John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, “You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format.”

CC licensed content, Shared previously

• Aromaticity. Authored by: Ramie Hosein. Located at: https://chem.libretexts.org/Textbook_Maps/Organic_Chemistry/Supplemental_Modules_(Organic_Chemistry)/Arenes/Properties_of_Arenes/Aromaticity. Project: Chemistry LibreTexts. License: CC BY-NC-SA: Attribution-NonCommercial-ShareAlike
• Aromatic. Authored by: Gamini Gunawardena from the OChemPal site (Utah Valley University). Located at: https://chem.libretexts.org/Ancillary_Materials/Reference/Organic_Chemistry_Glossary/Aromatic. Project: Chemistry LibreTexts. License: CC BY-NC-SA: Attribution-NonCommercial-ShareAlike

All rights reserved content

• 21.9: Hu00fcckel's 4n + 2 Rule. Authored by: John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8.. Located at: https://chem.libretexts.org/Textbook_Maps/Organic_Chemistry/Book%3A_Basic_Principles_of_Organic_Chemistry_(Roberts_and_Caserio)/21%3A_Resonance_and_Molecular_Orbital_Methods/21.09%3A_Huckel%27s_4n_2_Rule. Project: Chemistry LibreText. License: Other. License Terms: This content is copyrighted under the following conditions: You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format.