13.1: Introduction
- Page ID
- 225854
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Molecular Orbital Theory: Conjugation and Aromaticity
Let’s go back and consider again the simplest possible covalent bond: the one in molecular hydrogen (H2). When we described the hydrogen molecule using valence bond theory, we said that the two 1s orbitals from each atom overlap, allowing the two electrons to be shared and thus forming a covalent bond. In molecular orbital theory, we make a further statement: we say that the two atomic 1s orbitals mathematically combine to form two new orbitals. Recall that an atomic orbital (such as the 1s orbital of a hydrogen atom) describes a region of space around a single atom inside which electrons are likely to be found. A molecular orbital describes a region of space around two or more atoms inside which electrons are likely to be found.
Mathematical principles tell us that when orbitals combine, the number of orbitals before the combination takes place must equal the number of new orbitals that result from the combination – orbitals don’t just disappear! We saw this previously when we discussed hybrid orbitals: one s and three p orbitals make four sp3 hybrids. When two atomic 1s orbitals combine in the formation of H2, the result is two sigma ( σ) orbitals.

According to MO theory, one sigma orbital is lower in energy than either of the two isolated atomic 1s orbitals –this lower sigma orbital is referred to as a bonding molecular orbital. The second, ‘sigma star’ orbital is higher in energy than the two atomic 1s orbitals, and is referred to as an antibonding molecular orbital.
The bonding sigma orbital, which holds both electrons in the ground state of the molecule, is egg-shaped, encompassing the two nuclei, and with the highest likelihood of electrons being in the area between the two nuclei. The high-energy, antibonding sigma* orbital can be visualized as a pair of droplets, with areas of higher electron density near each nucleus and a ‘node’, (area of zero electron density) midway between the two nuclei.
Remember that we are thinking here about electron behavior as wave behavior. When two separate waves combine, they can do so with constructive interference, where the two amplitudes build up and reinforce one another, or destructive interference, where the two amplitudes cancel one another out. Bonding MOs are the consequence of constructive interference between two atomic orbitals, which results in an attractive interaction and an increase in electron density between the nuclei. Antibonding MO’s are the consequence of destructive interference which results in a repulsive interaction and a region of zero electron density between the nuclei (in other words, a node).
Following the same aufbau (‘building up’) principle you learned in General Chemistry for writing out electron configurations, we place the two electrons in the H2 molecule in the lowest energy molecular orbital, which is the (bonding) sigma orbital. The bonding (attracting) MO is full, and the antibonding (repulsing) MO is empty.
MO theory and conjugated pi bonds
The advantage of using MO theory to understand bonding in organic molecules becomes more apparent when we think about pi bonds. We find that the theory predicts that when we have a connected series of sp2 carbons, the pi bonds are said to be “conjugated.” In a conjugated system the pi bonds can be delocalized over the whole series of atoms, and this leads to additional stabilization. Note: Other second row sp2 atoms, such as oxygen and nitrogen, can also participate in this delocalization, as can sp hybridized atoms. If the conjugated system occurs in certain types of ring, such as a six-carbon benzene ring, it leads to exceptionally high stabilization called aromaticity, which we will discuss in section 13.5.
Aromaticity
Molecular orbital theory is especially helpful in explaining the unique properties of aromatic compounds such as benzene:
3D interactive model of benzene
Although benzene is most often drawn with three double bonds and three single bonds, in fact all of the carbon-carbon bonds iare exactly the same length (138 pm). In addition, the pi bonds in benzene are significantly less reactive than ‘normal’ pi bonds, either isolated or conjugated. Something about the structure of benzene makes its pi bonding arrangement especially stable. This ‘something’ has a name: it is called ‘aromaticity’.
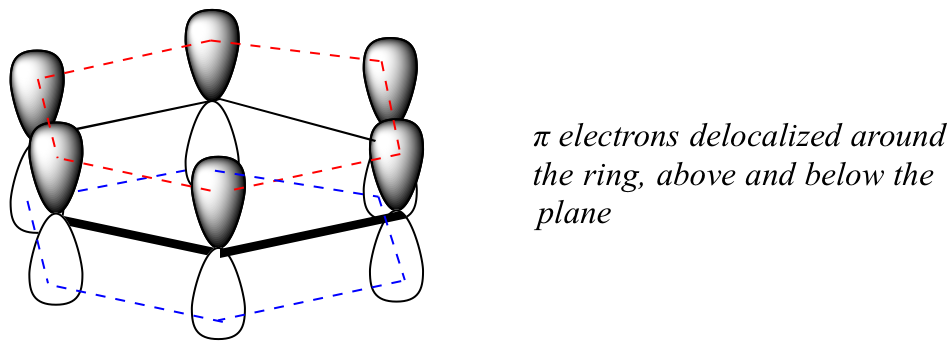
What exactly is this ‘aromatic’ property that makes the pi bonds in benzene so stable? In large part, the answer to this question lies in the fact that benzene is a cyclic molecule in which all of the ring atoms are sp2-hybridized. This allows the pi electrons to be delocalized in molecular orbitals that extend all the way around the ring, above and below the plane. For this to happen, of course, the ring must be planar – otherwise the p orbitals couldn’t overlap properly. Benzene is indeed known to be a flat molecule.
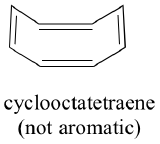
Do all cyclic molecules with alternating single and double bonds have this same aromatic stability? The answer, in fact, is ‘no’. The eight-membered cyclooctatetraene ring shown below is not flat, and its π bonds react like ‘normal’ alkenes.
Clearly it takes something more to be aromatic, and this can best be explained with molecular orbital theory. Let’s look at an energy diagram of the pi molecular orbitals in benzene.
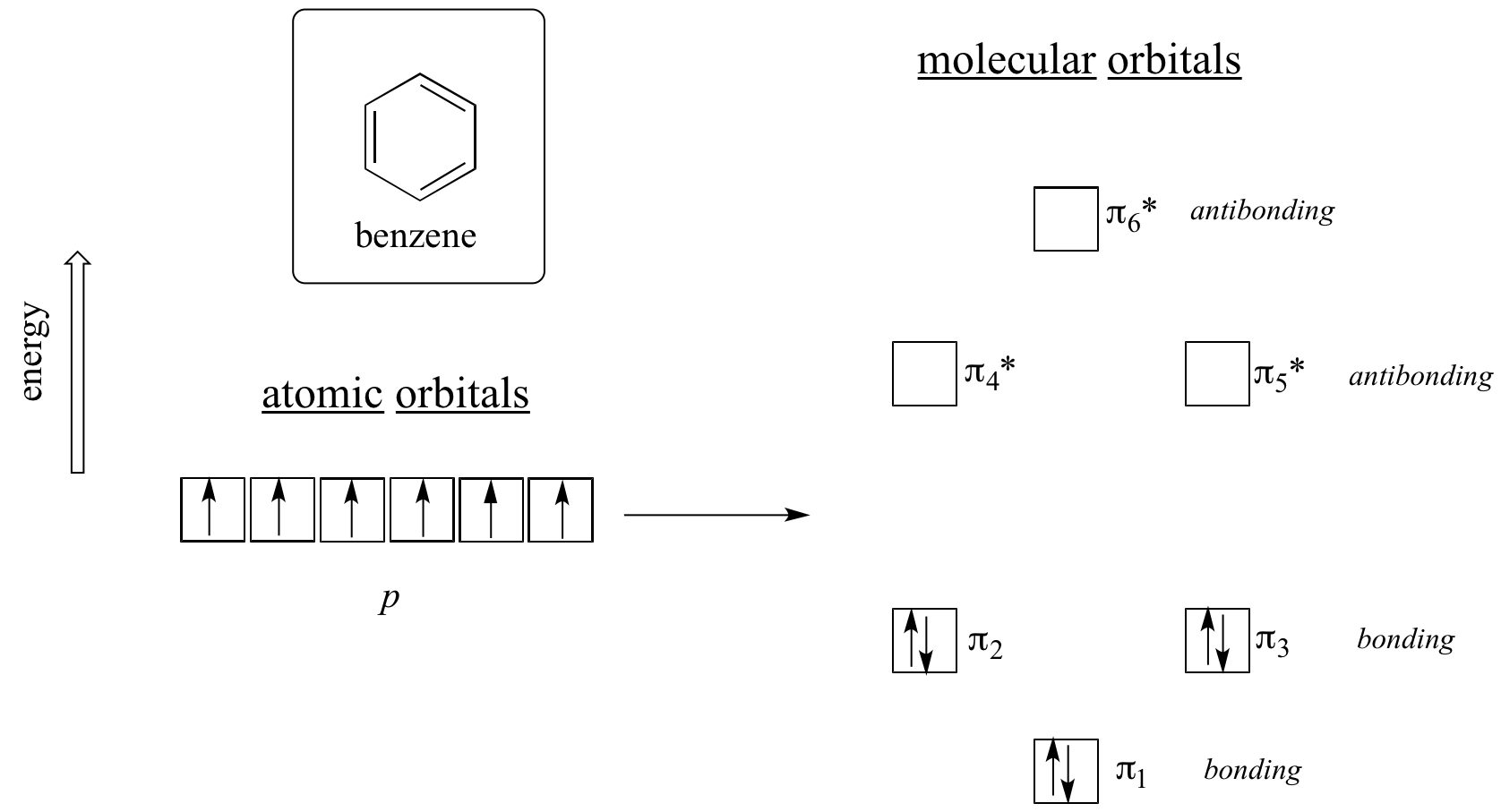
Quantum mechanical calculations tell us that the six pi molecular orbitals in benzene, formed from six atomic p orbitals, occupy four separate energy levels. pi1 and pi6* have unique energy levels, while the pi2 – pi3 and pi4*- pi5* pairs are degenerate, meaning they are at the same energy level. When we use the aufbau principle to fill up these orbitals with the six pi electrons in benzene, we see that the bonding orbitals are completely filled, and the antibonding orbitals are empty. This gives us a good clue to the source of the special stability of benzene: a full set of bonding MO’s is similar in many ways to the ‘full shell’ of electrons in the atomic orbitals of the stable noble gases helium, neon, and argon.
Now, let’s do the same thing for cyclooctatetraene, which we have already learned is not aromatic.
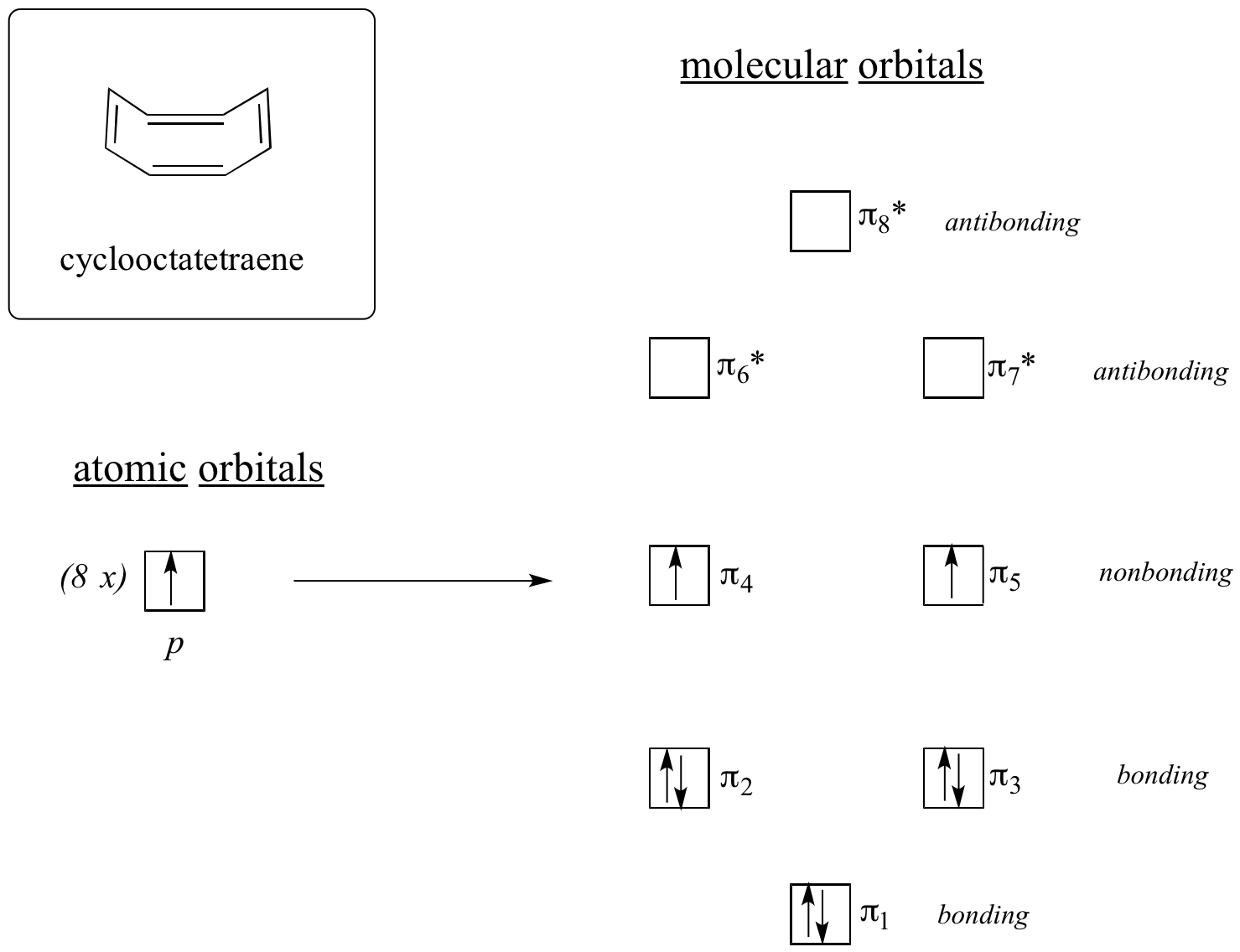
The result of molecular orbital calculations tells us that the lowest and highest energy MOs (pi1 and pi8*) have unique energy levels, while the other six form degenerate pairs. Notice that pi4 and pi5 are at the same energy level as the isolated 2pz atomic orbitals: these are therefore neither bonding nor antibonding, rather they are referred to as nonbonding MOs. Filling up the MOs with the eight pi electrons in the molecule, we find that the last two electrons are unpaired and fall into the two degenerate nonbonding orbitals. Because we don’t have a perfect filled shell of bonding MOs, our molecule is not aromatic. As a consequence, each of the double bonds in cyclooctatetraene acts more like an isolated double bond.
Here, then, are the conditions that must be satisfied for a molecule or group to be considered aromatic:
Criteria for aromaticity:
The molecule or group must be cyclic.
The ring must be planar.
Each atom in the ring must be sp2-hybridized.
The number of pi electrons in the ring must equal 4n+2, where n is any positive integer including zero.
Rule #4 is known as the Hückel rule, named after Erich Hückel, a German scientist who studied aromatic compounds in the 1930’s. If n = 0, the Hückel number is 2. If n = 1, the Hückel number is 6 (the Hückel number for benzene). The series continues with 10, 14, 18, 22, and so on. Cyclooctatetraene has eight pi electrons, which is not a Hückel number. Because six is such a common Hückel number, chemists often use the term ‘aromatic sextet’.
Benzene rings are ubiquitous in biomolecules and drugs – below are just a few examples.
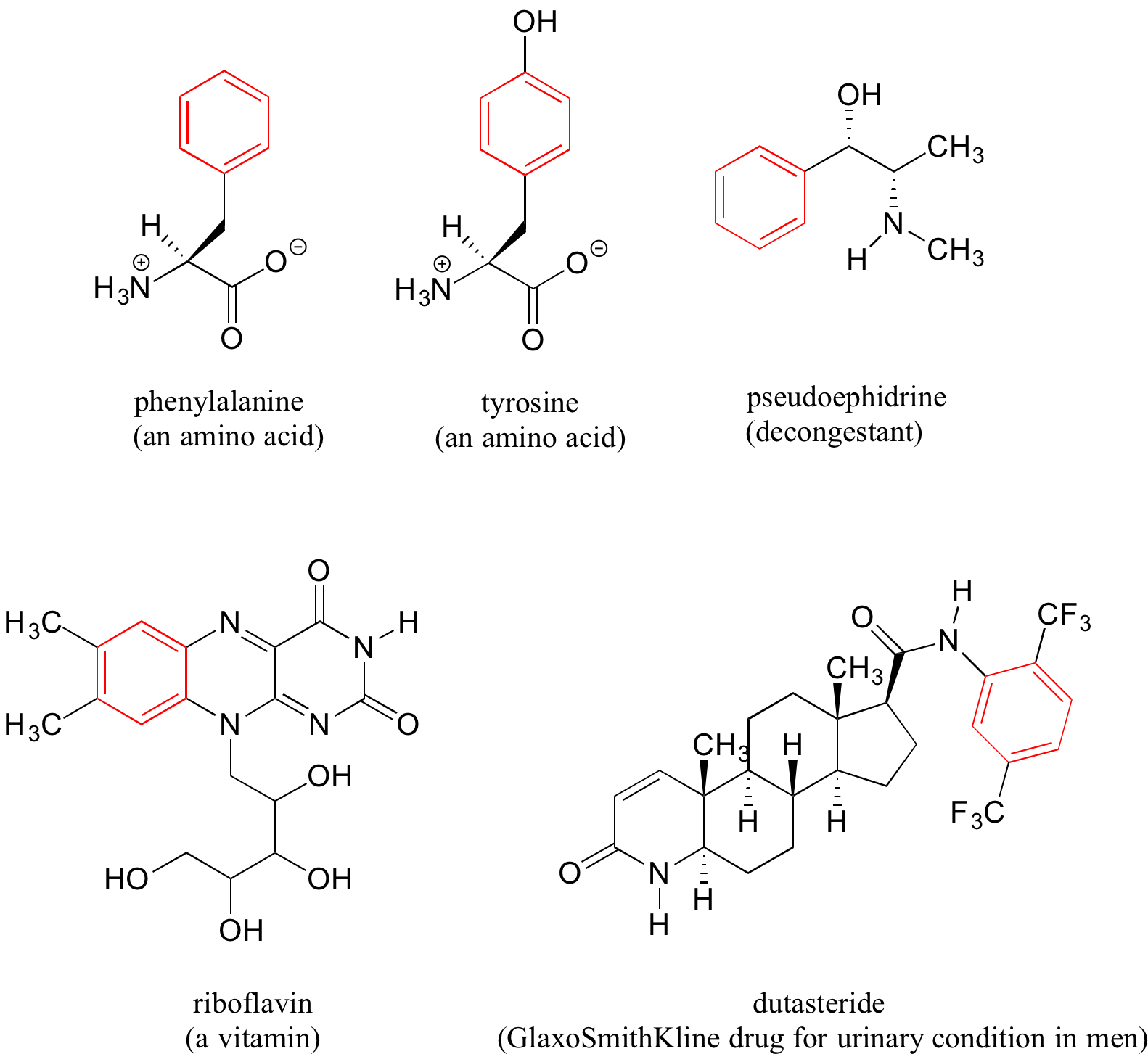
Recall that a benzene ring with a hydoxyl substituent -such as seen in the tyrosine structure above – is called a phenol.
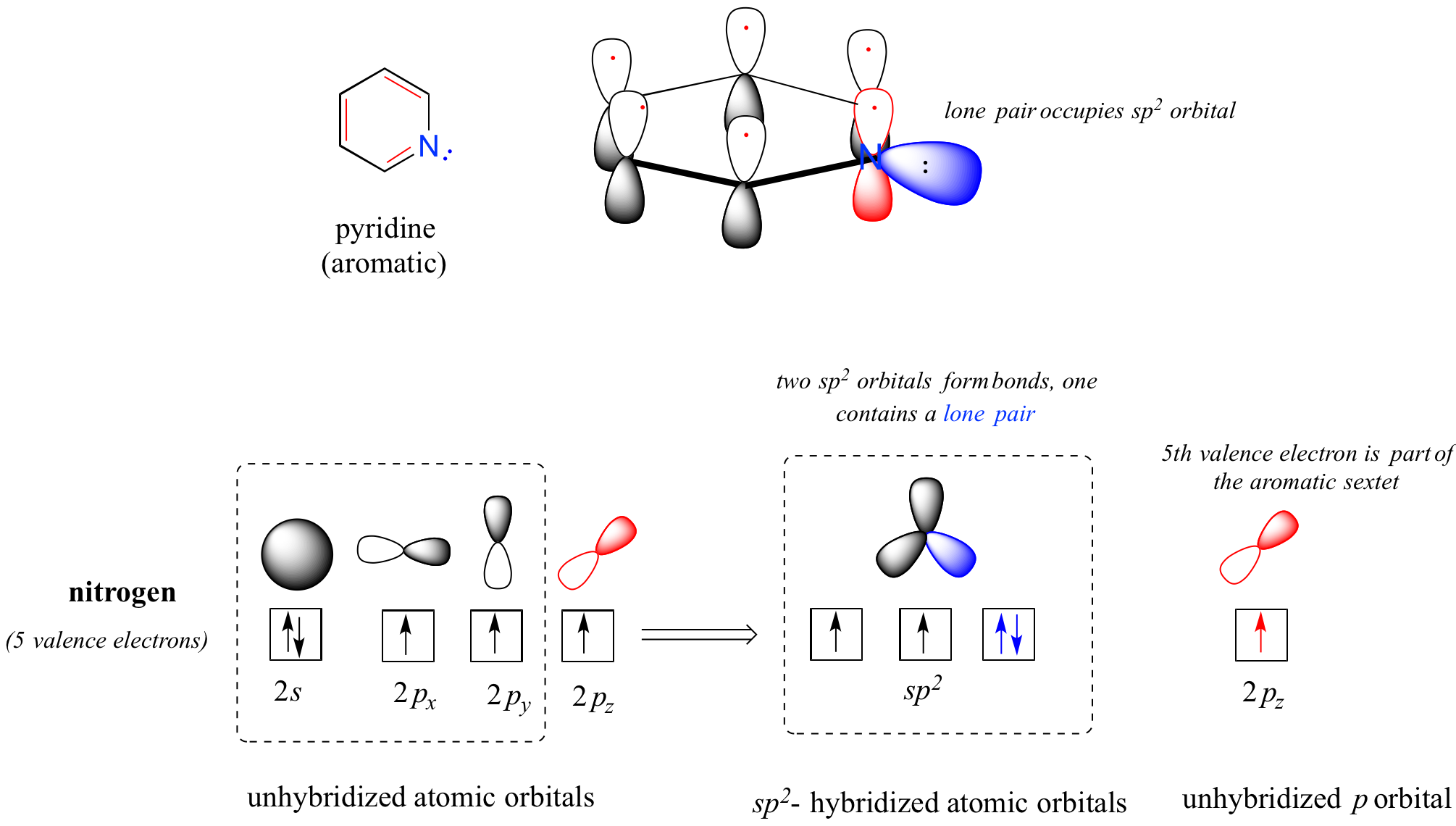
Heterocycles – cyclic structures in which the ring atoms may include oxygen or nitrogen – can also be aromatic. Pyridine, for example, is an aromatic heterocycle. In the bonding picture for pyridine, the nitrogen is sp2-hybridized, with two of the three sp2 orbitals forming sigma overlaps with the sp2 orbitals of neighboring carbon atoms, and the third nitrogen sp2 orbital containing the lone pair. The unhybridized p orbital contains a single electron, which is part of the 6 pi-electron system delocalized around the ring.
another image of orbitals in pyridine
Pyridoxine, commonly known as vitamin B6, and nicotine are both substituted pyridines.
Pyrrole is a five-membered aromatic heterocycle. In pyrrole, the lone pair electrons on the sp2-hybridized nitrogen are part of the aromatic sextet (contrast this to pyridine, where the lone pair occupies one of the sp2 hybrid orbitals).
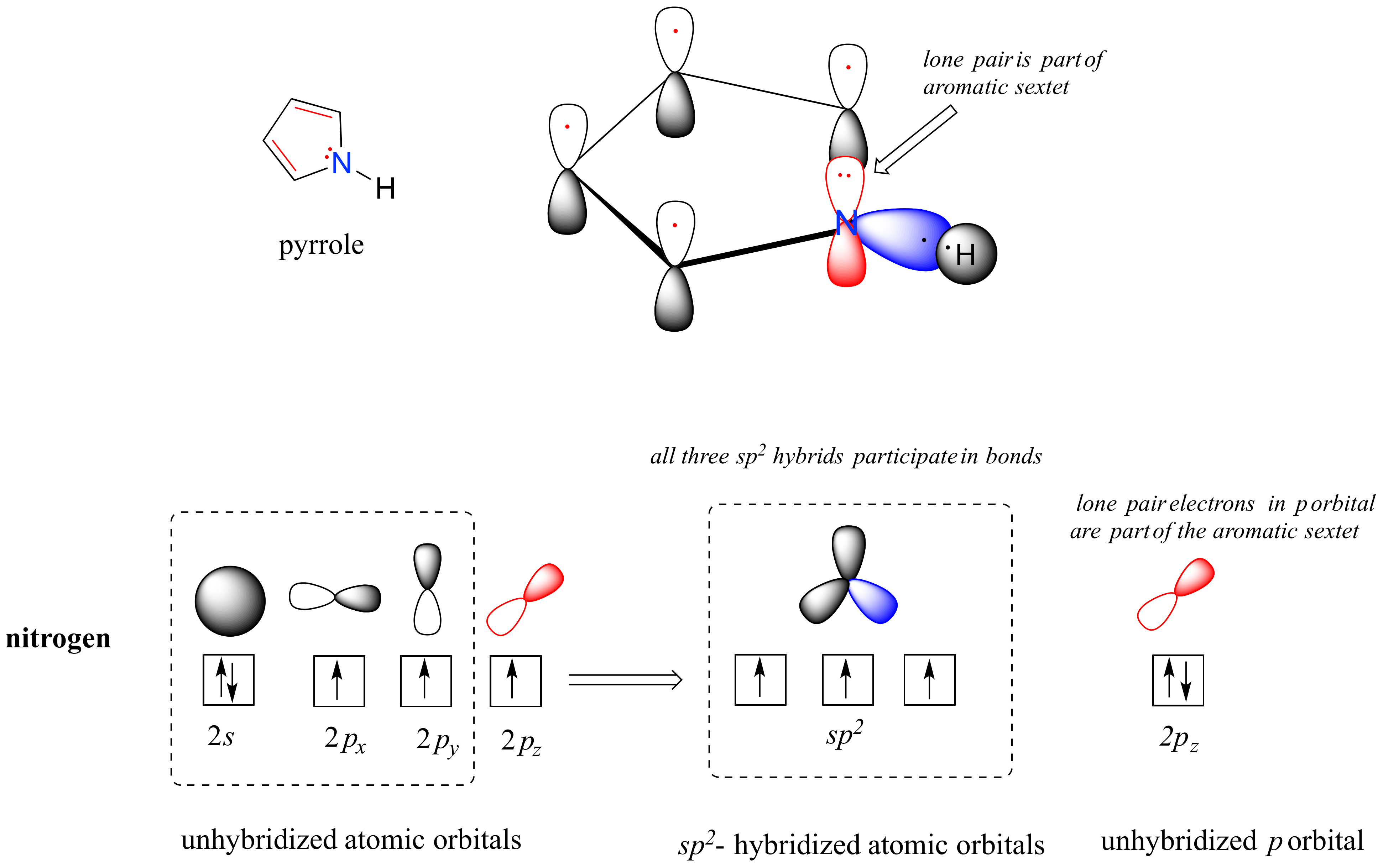
Why don’t we assume that the nitrogen in pyrrole is sp3-hybridized, like a normal secondary amine? The answer is simple: if it were, then pyrrole could not be aromatic, and thus it would not have the stability associated with aromaticity. In general, if a molecule or group can be aromatic, it will be, just as water will always flow downhill if there is a downhill pathway available.
Imidazole is another important example of an aromatic heterocycle found in biomolecules – the side chain of the amino acid histidine contains an imidazole ring.
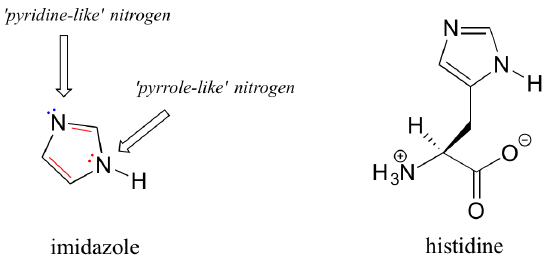
In imidazole, one nitrogen is ‘pyrrole-like’ (the lone pair contributes to the aromatic sextet) and one is ‘pyridine-like’ (the lone pair is located in an sp2 orbital, and is not part of the aromatic sextet).
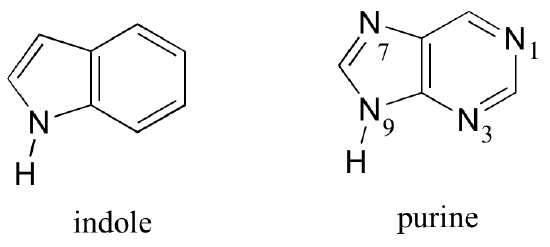
Fused-ring structures can also fulfill the Hückel criteria, and often have many of the same properties as monocyclic aromatic compounds, including a planar structure. Indole (a functional group on the side chain of the amino acid tryptophan) and purine (found in guanine and adenine nucleotide bases) both have a total of ten pi electrons delocalized around two rings.
The nucleic acid bases of DNA and RNA – guanine, adenine, cytosine, thymine, and uracil – are all aromatic systems, with the characteristic aromatic properties of planarity and delocalized p electron density. When you study the structure and function of DNA and RNA in a biochemistry or molecular biology course, you will see that the planar shape of the bases plays a critically important role.

Exercises
Exercise 2.11: Classify the nitrogen atoms of indole and purine as either ‘pyrrole-like’ or ‘pyridine-like’, in terms of where the lone pair electrons are located.
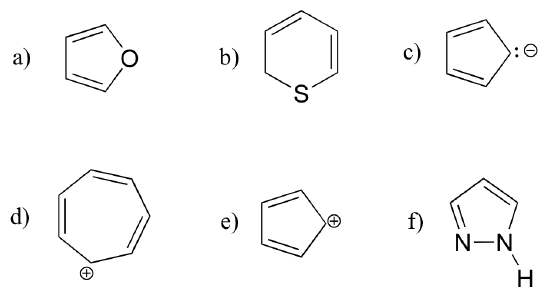
Exercise 2.12: Are the following molecules/ions aromatic? Explain, using criteria you learned in this section.
- 2.2: Molecular orbital theory: conjugation and aromaticity. Authored by: Tim Soderberg (University of Minnesota, Morris). Located at: https://chem.libretexts.org/Textbook_Maps/Organic_Chemistry/Book%3A_Organic_Chemistry_with_a_Biological_Emphasis_(Soderberg)/Chapter_02%3A_Introduction_to_organic_structure_and_bonding_II/2.2%3A_Molecular_orbital_theory%3A_conjugation_and_aromaticity. Project: Chemistry LibreTexts. License: CC BY-NC-SA: Attribution-NonCommercial-ShareAlike

