2.2: Molecular orbital theory: conjugation and aromaticity
- Page ID
- 1032
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
Valence bond theory does a remarkably good job at explaining the bonding geometry of many of the functional groups in organic compounds. There are some areas, however, where the valence bond theory falls short. It fails to adequately account, for example, for some interesting properties of compounds that contain alternating double and single bonds. In order to understand these properties, we need to think about chemical bonding in a new way, using the ideas of molecular orbital (MO) theory.
Let’s go back and consider again the simplest possible covalent bond: the one in molecular hydrogen (H2). When we described the hydrogen molecule using valence bond theory, we said that the two 1s orbitals from each atom overlap, allowing the two electrons to be shared and thus forming a covalent bond. In molecular orbital theory, we make a further statement: we say that the two atomic 1s orbitals mathematically combine to form two new orbitals. Recall that an atomic orbital (such as the 1s orbital of a hydrogen atom) describes a region of space around a single atom inside which electrons are likely to be found. A molecular orbital describes a region of space around two or more atoms inside which electrons are likely to be found.
Mathematical principles tell us that when orbitals combine, the number of orbitals before the combination takes place must equal the number of new orbitals that result from the combination – orbitals don’t just disappear! We saw this previously when we discussed hybrid orbitals: one s and three p orbitals make four sp3 hybrids. When two atomic 1s orbitals combine in the formation of H2, the result is two sigma (σ) orbitals.

Molecular orbitals for H2
According to MO theory, one sigma orbital is lower in energy than either of the two isolated atomic 1s orbitals –this lower sigma orbital is referred to as a bonding molecular orbital. The second, 'sigma star' orbital is higher in energy than the two atomic 1s orbitals, and is referred to as an antibonding molecular orbital.
The bonding sigma orbital, which holds both electrons in the ground state of the molecule, is egg-shaped, encompassing the two nuclei, and with the highest likelihood of electrons being in the area between the two nuclei. The high-energy, antibonding sigma* orbital can be visualized as a pair of droplets, with areas of higher electron density near each nucleus and a ‘node’, (area of zero electron density) midway between the two nuclei.
Remember that we are thinking here about electron behavior as wave behavior. When two separate waves combine, they can do so with constructive interference, where the two amplitudes build up and reinforce one another, or destructive interference, where the two amplitudes cancel one another out. Bonding MOs are the consequence of constructive interference between two atomic orbitals, which results in an attractive interaction and an increase in electron density between the nuclei. Antibonding MO’s are the consequence of destructive interference which results in a repulsive interaction and a region of zero electron density between the nuclei (in other words, a node).
Following the same aufbau ('building up') principle you learned in General Chemistry for writing out electron configurations, we place the two electrons in the H2 molecule in the lowest energy molecular orbital, which is the (bonding) sigma orbital. The bonding (attracting) MO is full, and the antibonding (repulsing) MO is empty.
MO theory and conjugated pi bonds
The advantage of using MO theory to understand bonding in organic molecules becomes more apparent when we think about pi bonds. Let’s first consider the pi bond in ethene from an MO theory standpoint (in this example we will be disregarding the s bonds in the molecule, and thinking only about the π bond). We start with two atomic orbitals: one unhybridized 2p orbital from each carbon. Each contains a single electron. In MO theory, the two atomic combine mathematically to form two pi molecular orbitals, one a low-energy pi bonding orbital and one a high-energy pi* antibonding orbital.
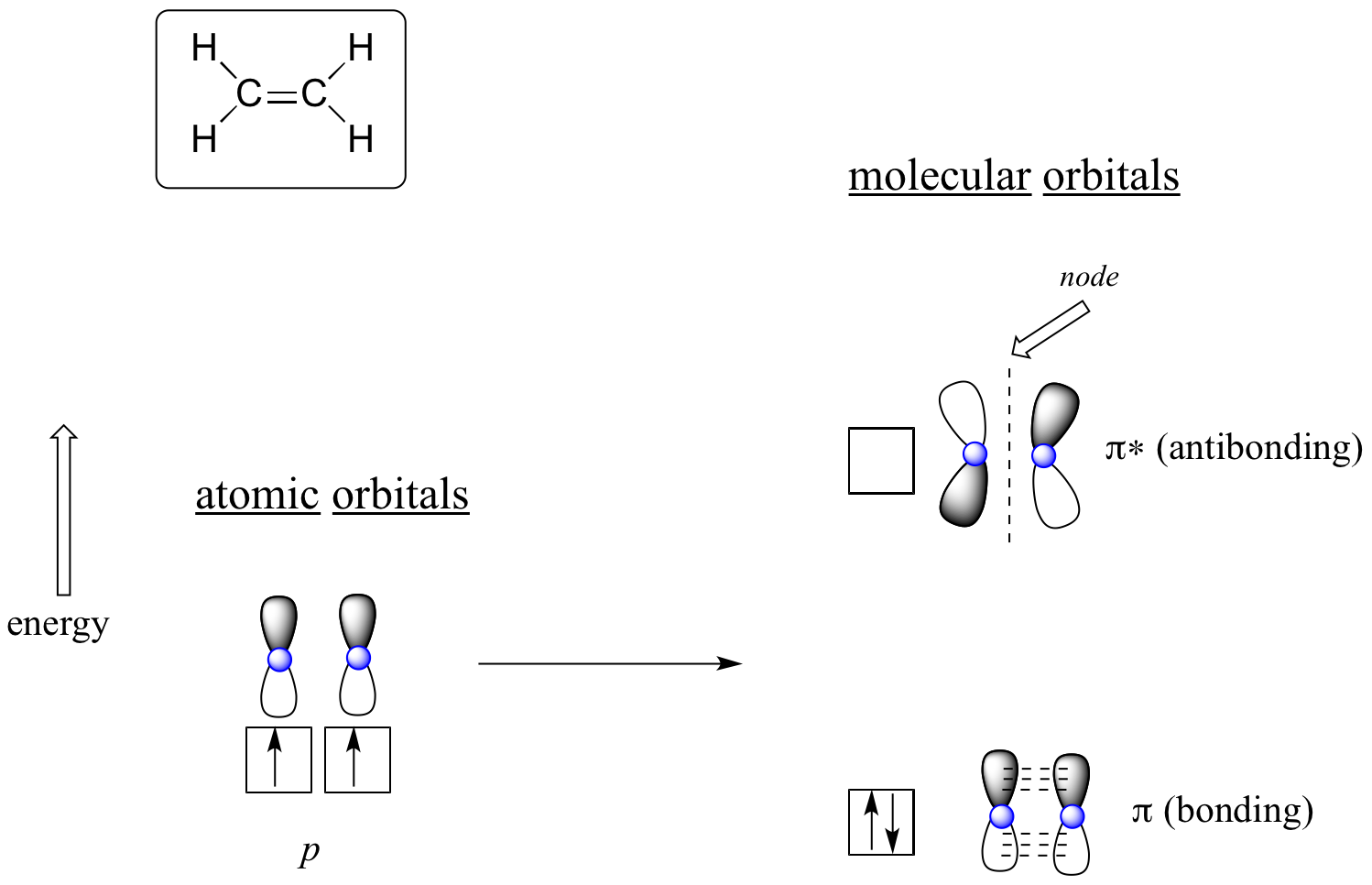
Molecular orbitals for ethene (ethylene)
In the bonding pi orbital, the two shaded lobes of the p orbitals interact constructively with each other, as do the two unshaded lobes (remember, the arbitrary shading choice represents mathematical (+) and (-) signs for the mathematical wavefunction describing the orbital). There is increased electron density between the two carbon nuclei in the molecular orbital - it is a bonding interaction.
In the higher-energy antibonding pi* orbital, the shaded lobe of one p orbital interacts destructively with the unshaded lobe of the second p orbital, leading to a node between the two nuclei and overall repulsion between the carbon nuclei.
Again using the 'building up' principle, we place the two electrons in the lower-energy, bonding pi molecular orbital. The antibonding pi* orbital remains empty.
Next, we'll consider the 1,3-butadiene molecule. From valence orbital theory alone we might expect that the C2-C3 bond in this molecule, because it is a sigma bond, would be able to rotate freely.

Experimentally, however, it is observed that there is a significant barrier to rotation about the C2-C3 bond, and that the entire molecule is planar. In addition, the C2-C3 bond is 148 pm long, shorter than a typical carbon-carbon single bond (about 154 pm), though longer than a typical double bond (about 134 pm).
Molecular orbital theory accounts for these observations with the concept of delocalized pi bonds. In this picture, the four 2p atomic orbitals combine mathematically to form four pi molecular orbitals of increasing energy. Two of these - the bonding pi orbitals - are lower in energy than the p atomic orbitals from which they are formed, while two - the antibonding pi* orbitals - are higher in energy.

The lowest energy molecular orbital, pi1, has only constructive interaction and zero nodes. Higher in energy, but still lower than the isolated p orbitals, the pi2 orbital has one node but two constructive interactions - thus it is still a bonding orbital overall. Looking at the two antibonding orbitals, pi3* has two nodes and one constructive interaction, while pi4* has three nodes and zero constructive interactions.
By the aufbau principle, the four electrons from the isolated 2pz atomic orbitals are placed in the bonding pi1 and pi2 MO’s. Because pi1 includes constructive interaction between C2 and C3, there is a degree, in the 1,3-butadiene molecule, of pi-bonding interaction between these two carbons, which accounts for its shorter length and the barrier to rotation. The valence bond picture of 1,3-butadiene shows the two pi bonds as being isolated from one another, with each pair of pi electrons ‘stuck’ in its own pi bond. However, molecular orbital theory predicts (accurately) that the four pi electrons are to some extent delocalized, or ‘spread out’, over the whole pi system.

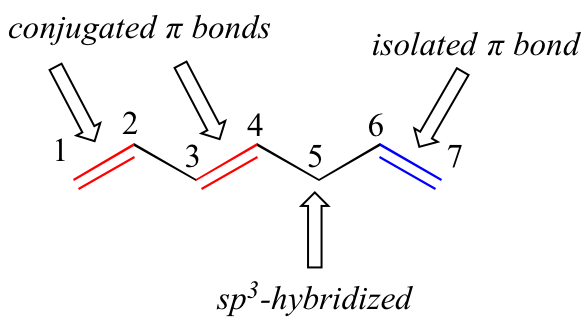
1,3-butadiene is the simplest example of a system of conjugated pi bonds. To be considered conjugated, two or more pi bonds must be separated by only one single bond – in other words, there cannot be an intervening sp3-hybridized carbon, because this would break up the overlapping system of parallel p orbitals. In the compound below, for example, the C1-C2 and C3-C4 double bonds are conjugated, while the C6-C7 double bond is isolated from the other two pi bonds by sp3-hybridized C5.
A very important concept to keep in mind is that there is an inherent thermodynamic stability associated with conjugation. This stability can be measured experimentally by comparing the heat of hydrogenation of two different dienes. (Hydrogenation is a reaction type that we will learn much more about in chapter 15: essentially, it is the process of adding a hydrogen molecule - two protons and two electrons - to a p bond). When the two conjugated double bonds of 1,3-pentadiene are 'hydrogenated' to produce pentane, about 225 kJ is released per mole of pentane formed. Compare that to the approximately 250 kJ/mol released when the two isolated double bonds in 1,4-pentadiene are hydrogenated, also forming pentane.
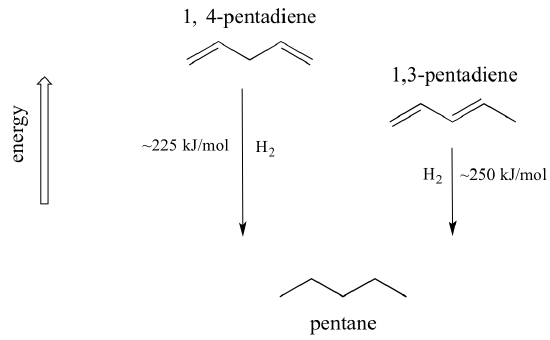
The conjugated diene is lower in energy: in other words, it is more stable. In general, conjugated pi bonds are more stable than isolated pi bonds.
Conjugated pi systems can involve oxygen and nitrogen atoms as well as carbon. In the metabolism of fat molecules, some of the key reactions involve alkenes that are conjugated to carbonyl groups.

In chapter 4, we will see that MO theory is very useful in explaining why organic molecules that contain extended systems of conjugated pi bonds often have distinctive colors. beta-carotene, the compound responsible for the orange color of carrots, has an extended system of 11 conjugated pi bonds.
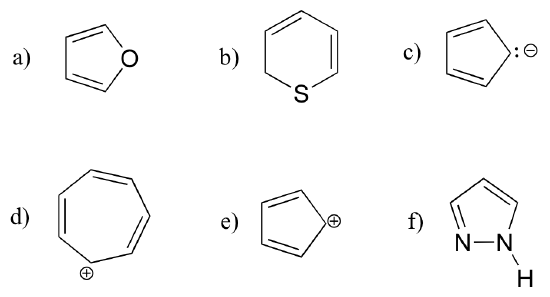
Exercise 2.9: Identify all conjugated and isolated double bonds in the structures below. For each conjugated pi system, specify the number of overlapping p orbitals, and how many pi electrons are shared among them.
Exercise 2.10: Identify all isolated and conjugated pi bonds in lycopene, the red-colored compound in tomatoes. How many pi electrons are contained in the conjugated pi system?

Aromaticity
Molecular orbital theory is especially helpful in explaining the unique properties of aromatic compounds such as benzene:
3D interactive model of benzene
Although benzene is most often drawn with three double bonds and three single bonds, in fact all of the carbon-carbon bonds iare exactly the same length (138 pm). In addition, the pi bonds in benzene are significantly less reactive than 'normal' pi bonds, either isolated or conjugated. Something about the structure of benzene makes its pi bonding arrangement especially stable. This ‘something’ has a name: it is called ‘aromaticity’.
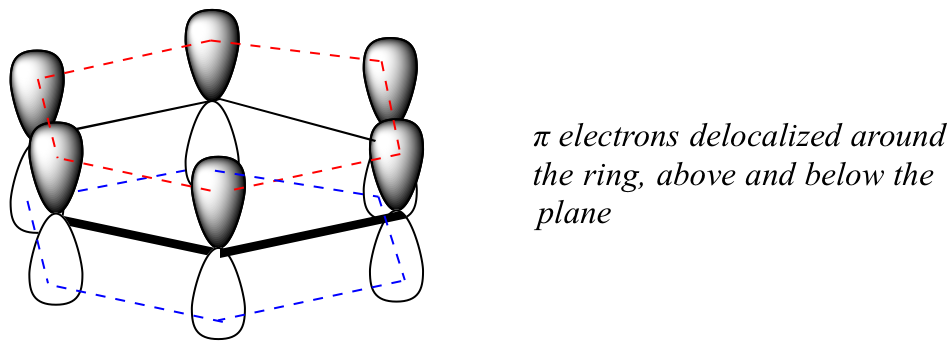
What exactly is this ‘aromatic’ property that makes the pi bonds in benzene so stable? In large part, the answer to this question lies in the fact that benzene is a cyclic molecule in which all of the ring atoms are sp2-hybridized. This allows the pi electrons to be delocalized in molecular orbitals that extend all the way around the ring, above and below the plane. For this to happen, of course, the ring must be planar – otherwise the p orbitals couldn’t overlap properly. Benzene is indeed known to be a flat molecule.
Do all cyclic molecules with alternating single and double bonds have this same aromatic stability? The answer, in fact, is ‘no’. The eight-membered cyclooctatetraene ring shown below is not flat, and its π bonds react like 'normal' alkenes.
Clearly it takes something more to be aromatic, and this can best be explained with molecular orbital theory. Let’s look at an energy diagram of the pi molecular orbitals in benzene.
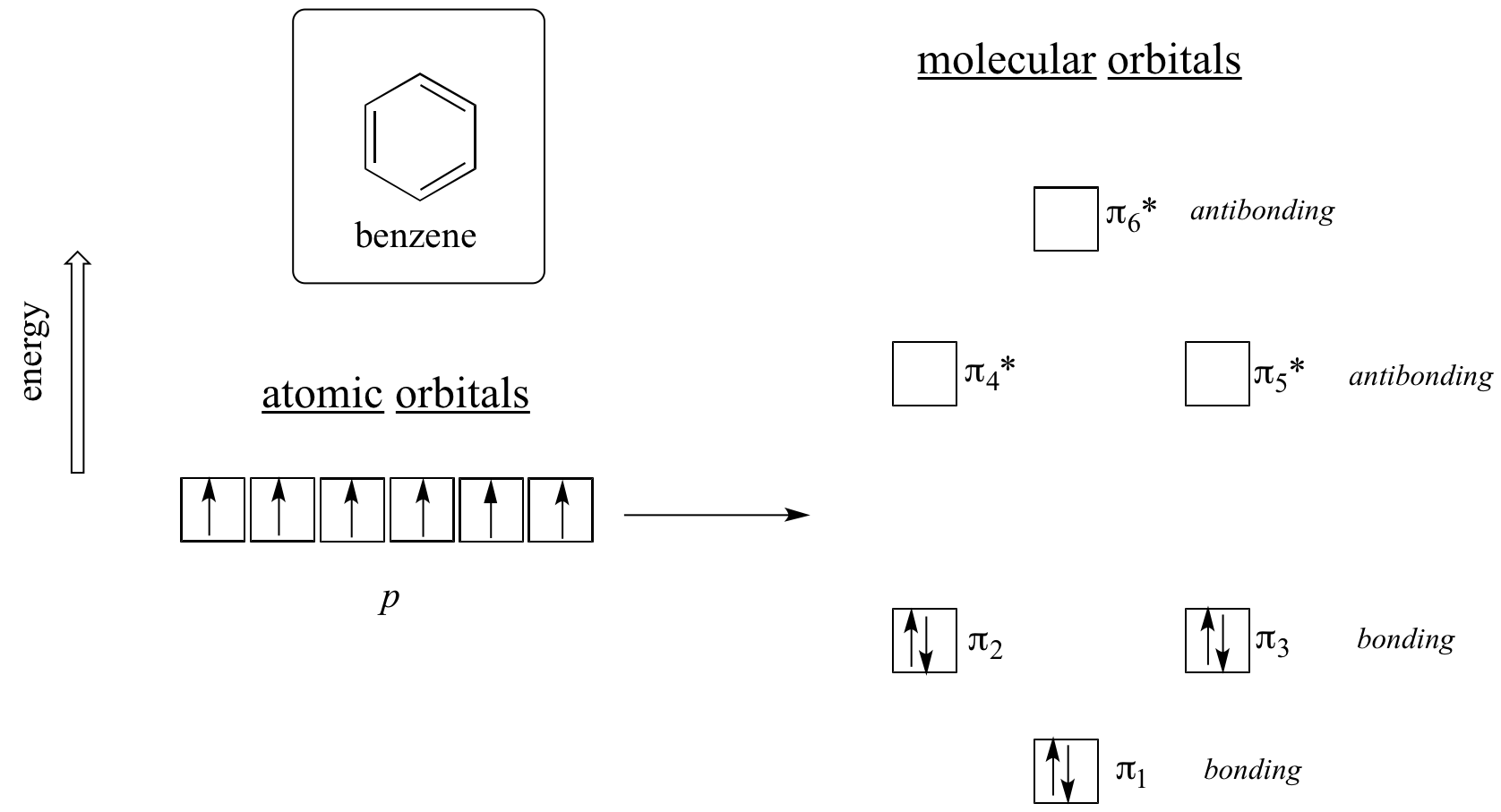
Quantum mechanical calculations tell us that the six pi molecular orbitals in benzene, formed from six atomic p orbitals, occupy four separate energy levels. pi1 and pi6* have unique energy levels, while the pi2 - pi3 and pi4*- pi5* pairs are degenerate, meaning they are at the same energy level. When we use the aufbau principle to fill up these orbitals with the six pi electrons in benzene, we see that the bonding orbitals are completely filled, and the antibonding orbitals are empty. This gives us a good clue to the source of the special stability of benzene: a full set of bonding MO’s is similar in many ways to the ‘full shell’ of electrons in the atomic orbitals of the stable noble gases helium, neon, and argon.
Now, let’s do the same thing for cyclooctatetraene, which we have already learned is not aromatic.
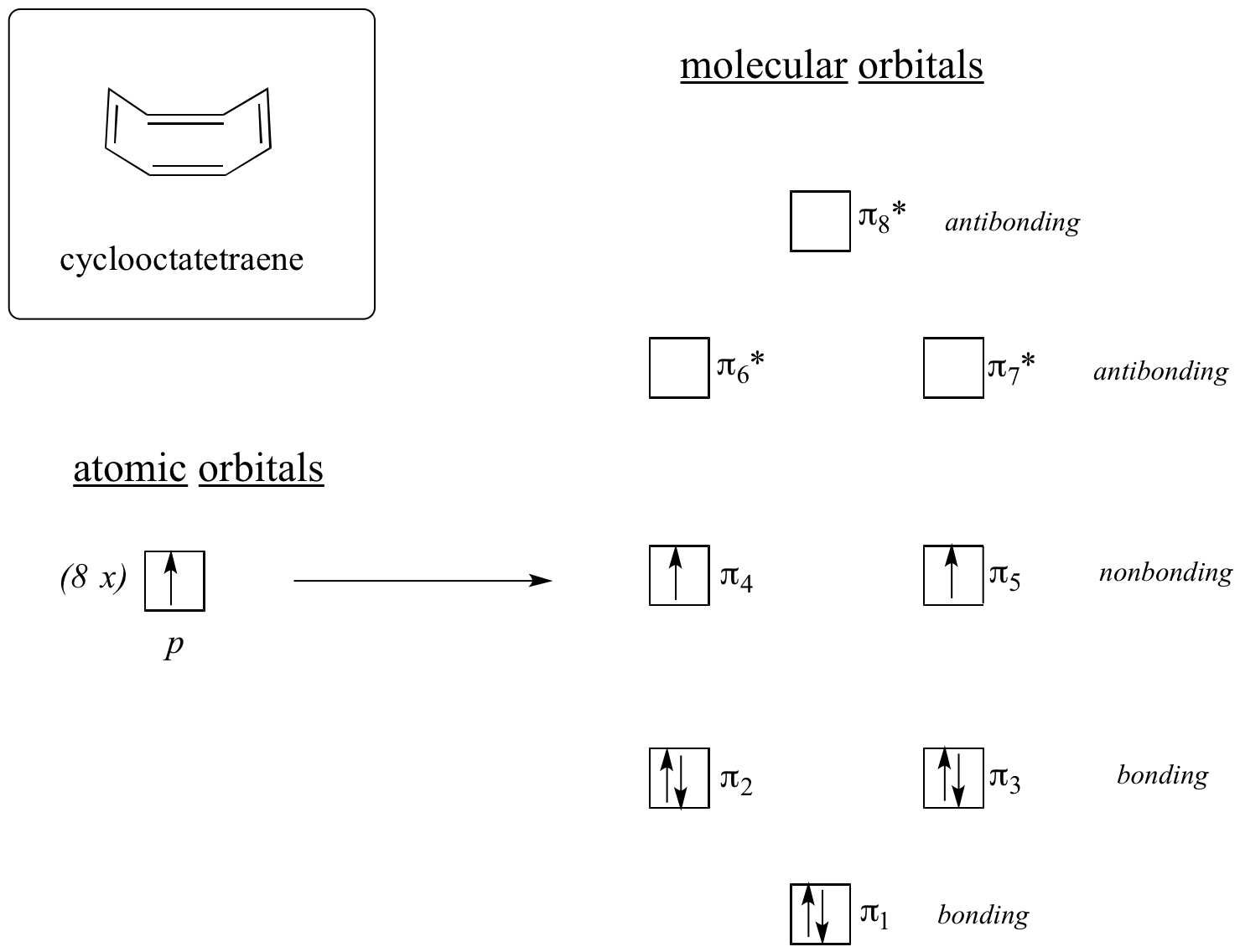
The result of molecular orbital calculations tells us that the lowest and highest energy MOs (pi1 and pi8*) have unique energy levels, while the other six form degenerate pairs. Notice that pi4 and pi5 are at the same energy level as the isolated 2pz atomic orbitals: these are therefore neither bonding nor antibonding, rather they are referred to as nonbonding MOs. Filling up the MOs with the eight pi electrons in the molecule, we find that the last two electrons are unpaired and fall into the two degenerate nonbonding orbitals. Because we don't have a perfect filled shell of bonding MOs, our molecule is not aromatic. As a consequence, each of the double bonds in cyclooctatetraene acts more like an isolated double bond.
Here, then, are the conditions that must be satisfied for a molecule or group to be considered aromatic:
Criteria for aromaticity:
The molecule or group must be cyclic.
The ring must be planar.
Each atom in the ring must be sp2-hybridized.
The number of pi electrons in the ring must equal 4n+2, where n is any positive integer including zero.
Rule #4 is known as the Hückel rule, named after Erich Hückel, a German scientist who studied aromatic compounds in the 1930’s. If n = 0, the Hückel number is 2. If n = 1, the Hückel number is 6 (the Hückel number for benzene). The series continues with 10, 14, 18, 22, and so on. Cyclooctatetraene has eight pi electrons, which is not a Hückel number. Because six is such a common Hückel number, chemists often use the term 'aromatic sextet'.
Benzene rings are ubiquitous in biomolecules and drugs - below are just a few examples.

Recall that a benzene ring with a hydoxyl substituent -such as seen in the tyrosine structure above - is called a phenol.
Heterocycles - cyclic structures in which the ring atoms may include oxygen or nitrogen - can also be aromatic. Pyridine, for example, is an aromatic heterocycle. In the bonding picture for pyridine, the nitrogen is sp2-hybridized, with two of the three sp2 orbitals forming sigma overlaps with the sp2 orbitals of neighboring carbon atoms, and the third nitrogen sp2 orbital containing the lone pair. The unhybridized p orbital contains a single electron, which is part of the 6 pi-electron system delocalized around the ring.
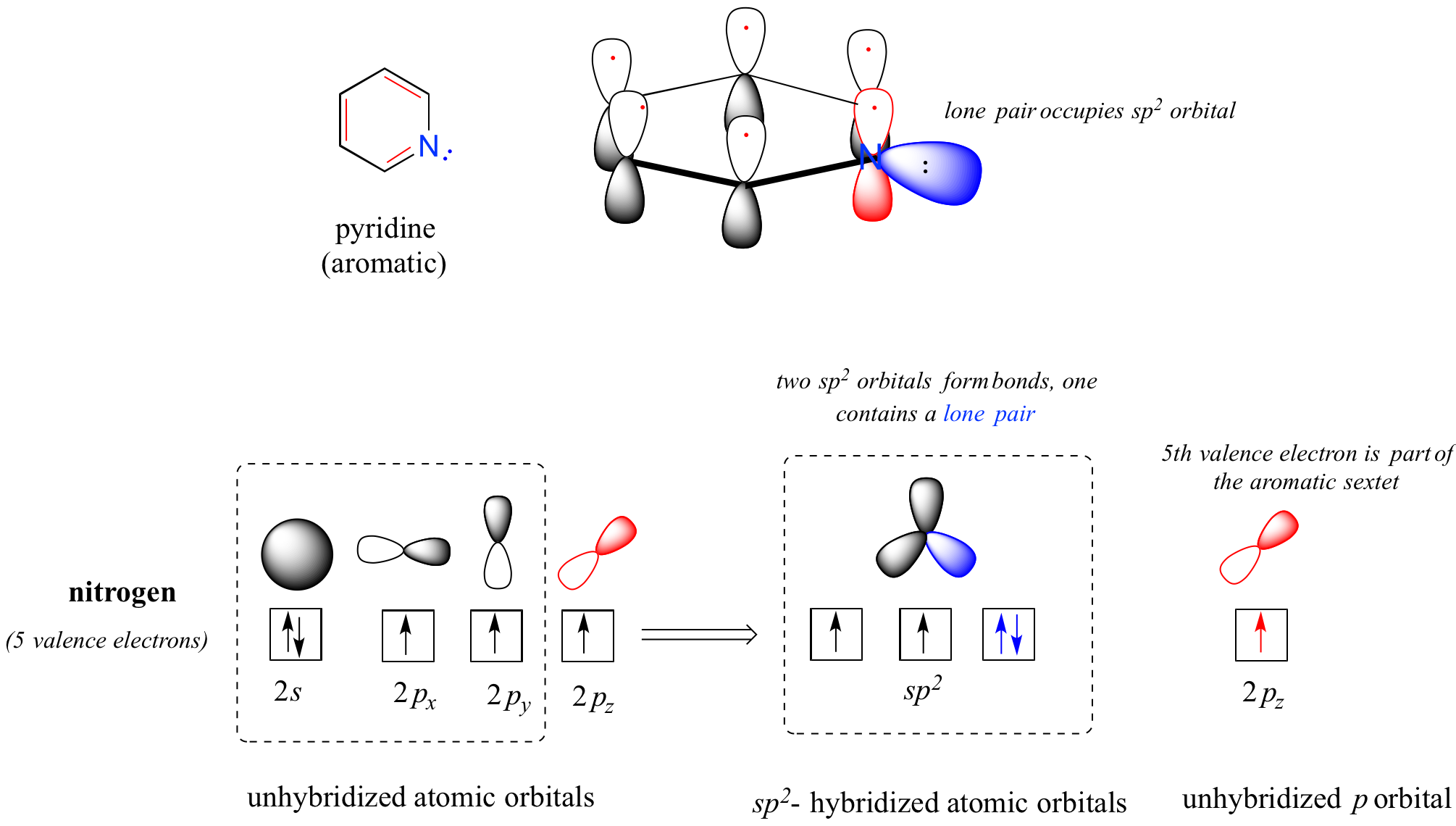
another image of orbitals in pyridine
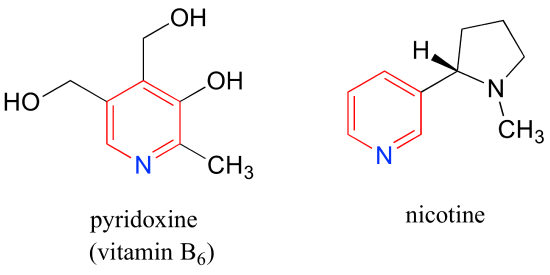
Pyridoxine, commonly known as vitamin B6, and nicotine are both substituted pyridines.
Pyrrole is a five-membered aromatic heterocycle. In pyrrole, the lone pair electrons on the sp2-hybridized nitrogen are part of the aromatic sextet (contrast this to pyridine, where the lone pair occupies one of the sp2 hybrid orbitals).
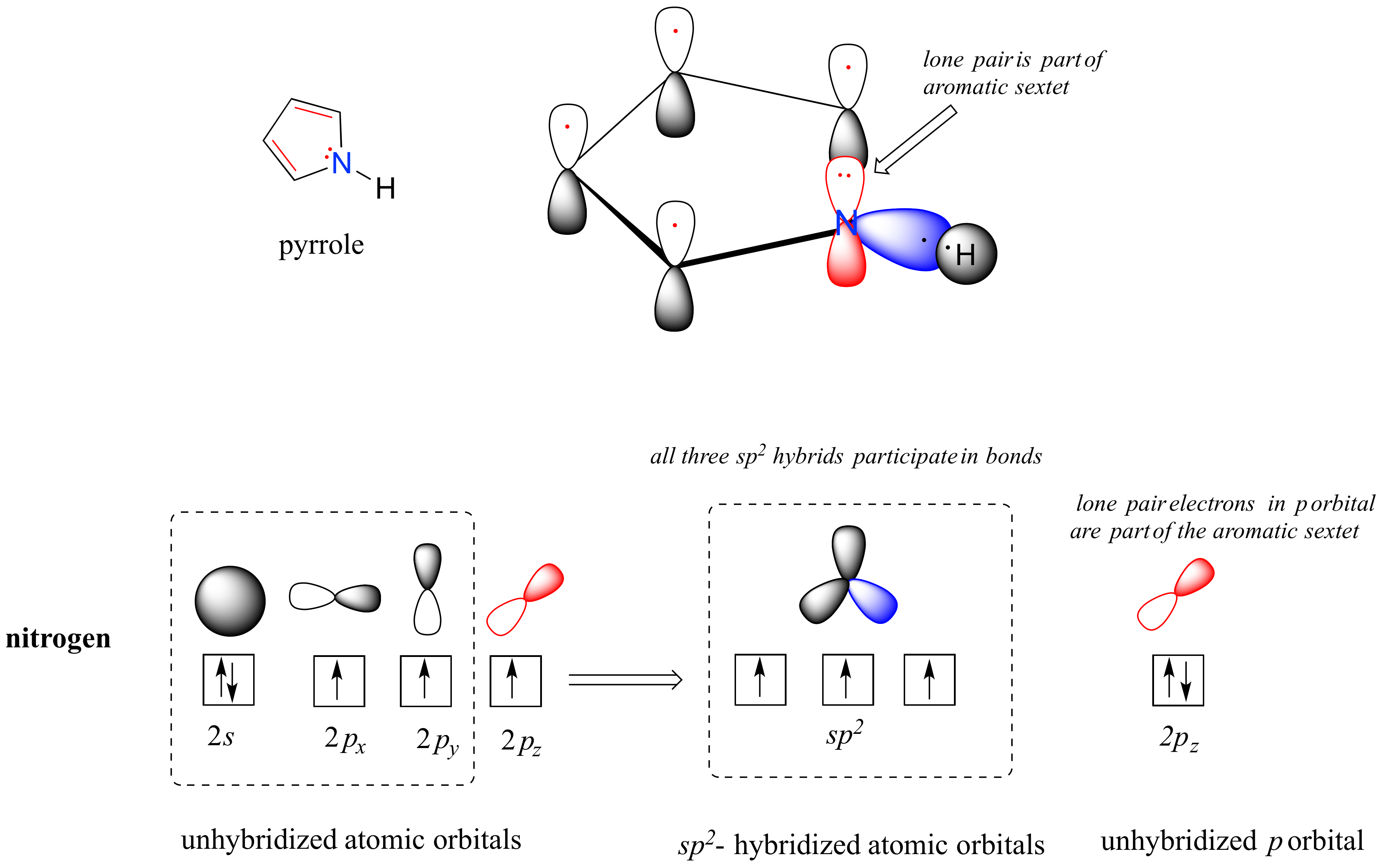
Why don't we assume that the nitrogen in pyrrole is sp3-hybridized, like a normal secondary amine? The answer is simple: if it were, then pyrrole could not be aromatic, and thus it would not have the stability associated with aromaticity. In general, if a molecule or group can be aromatic, it will be, just as water will always flow downhill if there is a downhill pathway available.
Imidazole is another important example of an aromatic heterocycle found in biomolecules - the side chain of the amino acid histidine contains an imidazole ring.

In imidazole, one nitrogen is 'pyrrole-like' (the lone pair contributes to the aromatic sextet) and one is 'pyridine-like' (the lone pair is located in an sp2 orbital, and is not part of the aromatic sextet).
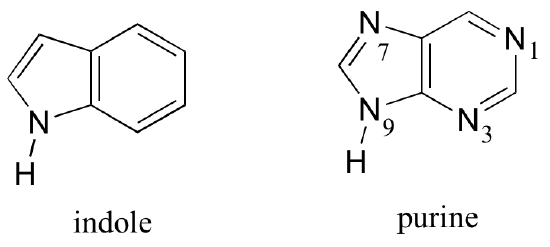
Fused-ring structures can also fulfill the Hückel criteria, and often have many of the same properties as monocyclic aromatic compounds, including a planar structure. Indole (a functional group on the side chain of the amino acid tryptophan) and purine (found in guanine and adenine nucleotide bases) both have a total of ten pi electrons delocalized around two rings.
The nucleic acid bases of DNA and RNA - guanine, adenine, cytosine, thymine, and uracil - are all aromatic systems, with the characteristic aromatic properties of planarity and delocalized p electron density. When you study the structure and function of DNA and RNA in a biochemistry or molecular biology course, you will see that the planar shape of the bases plays a critically important role.

Exercise 2.11: Classify the nitrogen atoms of indole and purine as either 'pyrrole-like' or 'pyridine-like', in terms of where the lone pair electrons are located.
Exercise 2.12: Are the following molecules/ions aromatic? Explain, using criteria you learned in this section.