9.5: The Basis for Differences in Chemical Shift
- Page ID
- 234540
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Diamagnetic shielding and deshielding
We come now to the question of why nonequivalent protons have different resonance frequencies and thus different chemical shifts. The chemical shift of a given proton is determined primarily by interactions with the nearby electrons. The most important thing to understand is that when electrons are subjected to an external magnetic field, they form their own small induced magnetic fields in opposition to the external field.
Consider the methane molecule (\(CH_4\)) in which the four equivalent protons have a chemical shift of 0.23 ppm (this is a value we can look up in any chemistry reference source). The valence electrons around the methyl carbon, when subjected to B0, generate their own very small induced magnetic field that opposes \(B_0\). This induced field, to a small but significant degree, shields the nearby protons from experiencing the full force of \(B_0\), an effect known as local diamagnetic shielding. In other words, the methane protons do not quite experience the full force of \(B_0\) - what they experience is called \(B_{eff}\), or the effective field, which is slightly weaker than \(B_0\) due to the influence of the nearby electrons.

Because \(B_{eff}\) is slightly weaker than B0, the resonance frequency (and thus the chemical shift) of the methane proton is slightly lower than what it would be if it did not have electrons nearby and was feeling the full force of \(B_0\). (You should note that the figure above is not to scale: the applied field is generated by a superconducting magnet and is extremely strong, while the opposing induced field from the electrons is comparatively very small.)
Now consider methyl fluoride, CH3F, in which the protons have a chemical shift of 4.26 ppm, significantly higher than that of methane. This is caused by something called the deshielding effect. Recall that fluorine is very electronegative: it pulls electrons towards itself, effectively decreasing the electron density around each of the protons. For the protons, being in a lower electron density environment means less diamagnetic shielding, which in turn means a greater overall exposure to \(B_0\), a stronger \(B_{eff}\), and a higher resonance frequency. Put another way, the fluorine, by pulling electron density away from the protons, is deshielding them, leaving them more exposed to \(B_0\). As the electronegativity of the substituent increases, so does the extent of deshielding, and so does the chemical shift. This is evident when we look at the chemical shifts of methane and three halomethane compounds (remember that electronegativity increases as we move up a column in the periodic table, so flourine is the most electronegative and bromine the least).
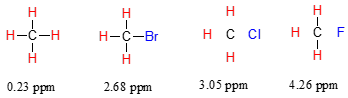
To a large extent, then, we can predict trends in chemical shift by considering how much deshielding is taking place near a proton.
The chemical shift of trichloromethane (common name chloroform) is, as expected, higher than that of dichloromethane, which is in turn higher than that of chloromethane.
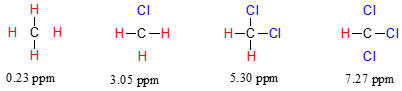
The deshielding effect of an electronegative substituent diminishes sharply with increasing distance:

The presence of an electronegative oxygen, nitrogen, sulfur, or \(sp^2\)-hybridized carbon also tends to shift the NMR signals of nearby protons slightly downfield:

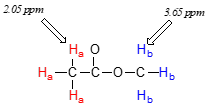
Now we can finally assign the two peaks in the the \(^1H\)-NMR spectrum of methyl acetate. We can predict that the methyl ester protons (\(H_b\)), which are deshielded by the adjacent oxygen atom, will have a higher chemical shift than the acetate protons (\(H_a\)), which are deshielded to a lesser extent by the carbonyl group. Therefore, the signal at 3.7 must correspond to \(H_b\), and the signal at 2.0 to \(H_a\).
Diamagnetic anisotropy
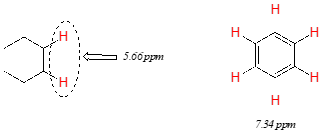
Vinylic protons (those directly bonded to an alkene carbon) and aromatic protons resonate much further downfield than can be accounted for simply by the deshielding effect of nearby electronegative atoms. Note the chemical shifts of the vinylic and aromatic protons in cyclohexene and benzene:
We'll consider the aromatic proton first. Recall that in benzene and many other aromatic structures, a sextet of p electrons is delocalized around the ring. When the molecule is exposed to \(B_0\), these \(p\) electrons begin to circulate in a ring current, generating their own induced magnetic field that opposes \(B_0\). In this case, however, the induced field of the \(p\) electrons does not shield the aromatic protons from \(B_0\) as you might expect– rather, it causes the protons to experience a stronger magnetic field in the direction of \(B_0\) – in other words, it adds to \(B_0\) rather than subtracting from it.
To understand how this happens, we need to understand the concept of diamagnetic anisotropy (anisotropy means `non-uniformity`). So far, we have been picturing magnetic fields as being oriented in a uniform direction. This is only true over a small area. If we step back and take a wider view, however, we see that the lines of force in a magnetic field are actually anisotropic. They start in the 'north' direction, then loop around like a snake biting its own tail.
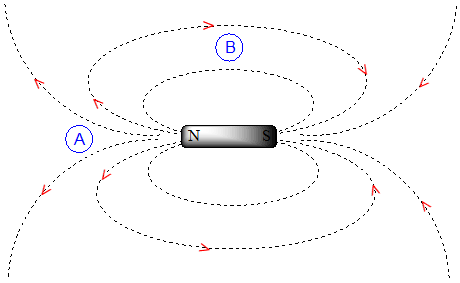
If we are at point A in the figure above, we feel a magnetic field pointing in a northerly direction. If we are at point B, however, we feel a field pointing to the south.
In the induced field generated by the aromatic ring current, the aromatic protons are at the equivalent of ‘point B’ – this means that the induced current in this region of space is oriented in the same direction as \(B_0\), so it adds to \(B_0\) rather than subtracting from it.
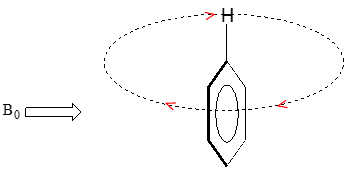
The end result is that aromatic protons, due to the anisotropy of the induced field generated by the \(pi \) ring current, appear to be highly deshielded. Their chemical shift is far downfield, in the 6.5-8 ppm region.
Diamagnetic anisotropy is also responsible for the downfield chemical shifts of vinylic protons (4.5-6.5 ppm) and aldehyde protons (9-10 ppm). These groups are not aromatic and thus do not generate ring currents does benzene, but the p electrons circulate in such a way as to generate a magnetic field that adds to \(B_0\) in the regions of space occupied by the protons. Carboxylic acid protons are very far downfield (10-12 ppm) due to the combined influence of the electronegative oxygen atom and the nearby \(pi \) bond.
Hydrogen bonded protons
Protons that are directly bonded to oxygen or nitrogen have chemical shifts that can vary widely depending on solvent and concentration. These protons can participate to varying degrees in hydrogen bonding interactions, and the degree hydrogen bonding greatly influences the electron density around the proton - and thus the chemical shift. Signals for hydrogen bonding protons also tend to be broader than those of hydrogens bonded to carbon, a phenomenon that is also due to hydrogen bonding.
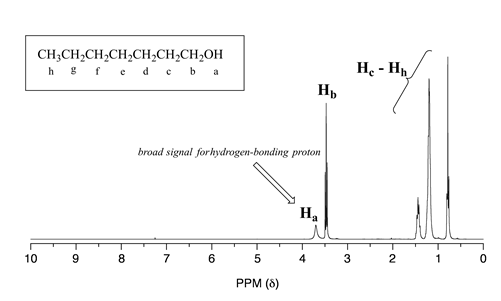
Alcohol protons, for example, will usually show broad signals anywhere between 1-5 ppm. The signal for \(H_a\) in the spectrum of 1-heptanol is a typical example of a broadened NMR signal for an alcohol proton.
The table below provides a summary of approximate chemical shift ranges for protons in different bonding arrangements. A more detailed table can be found in the appendix.
| Type of proton | Chemical shift range (ppm) |
|---|---|
| bonded to \(sp^3\) carbon | 0.5 - 4 |
| bonded to \(N\) (amine) | 1 - 3 |
| bonded to \(O\) (alcohol) | 1 - 5 |
| alkene/ vinylic | 3.5 - 6.5 |
| terminal alkyne | 2 - 3 |
| bonded to \(N\) (amide) | 5 - 9 |
| aromatic | 6 - 9 |
| aldehyde | 9.5 - 10 |
| carboxylic acid | 10 - 13 |
Exercise \(\PageIndex{1}\)
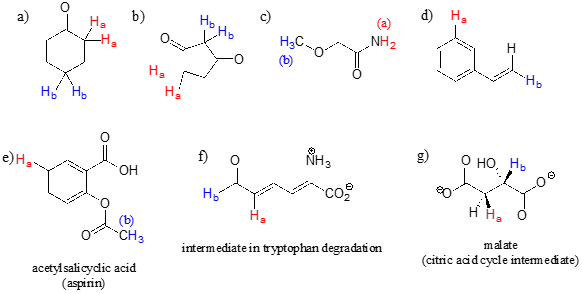
For each pair of protons colored red (\(H_a\)) and blue (\(H_b\)) in the structures below, state which is expected to have the higher chemical shift in \(^1H\)-NMR. For some of these it will be helpful to consult Table 2 at the back of the book.
Exercise \(\PageIndex{2}\)
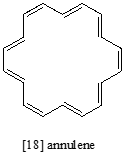
The \(^1H\)-NMR spectrum of the aromatic compound [18] annulene has two peaks, at 8.9 ppm and -1.8 ppm (a negative chemical shift, upfield of TMS!) with an integration ratio of 2:1. Explain the unusual chemical shift of the latter peak.
Contributors
Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)


