4.1 Chirality
- Page ID
- 14996
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Chirality and Stereoisomers
Stereoisomers are isomers that differ in spatial arrangement of atoms, rather than order of atomic connectivity. One of their most interesting type of isomer is the mirror-image stereoisomers, a non-superimposable set of two molecules that are mirror image of one another. The existence of these molecules are determined by concept known as chirality.
Introduction
Organic compounds, molecules created around a chain of carbon atom (more commonly known as carbon backbone), play an essential role in the chemistry of life. These molecules derive their importance from the energy they carry, mainly in a form of potential energy between atomic molecules. Since such potential force can be widely affected due to changes in atomic placement, it is important to understand the concept of an isomer, a molecule sharing same atomic make up as another but differing in structural arrangements. This article will be devoted to a specific isomers called stereoisomers and its property of chirality (Figure 1).
The concepts of steroisomerism and chirality command great deal of importance in modern organic chemistry, as these ideas helps to understand the physical and theoretical reasons behind the formation and structures of numerous organic molecules, the main reason behind the energy embedded in these essential chemicals. In contrast to more well-known constitutional isomerism, which develops isotopic compounds simply by different atomic connectivity, stereoisomerism generally maintains equal atomic connections and orders of building blocks as well as having same numbers of atoms and types of elements.
What, then, makes stereoisomers so unique? To answer this question, the learner must be able to think and imagine in not just two-dimensional images, but also three-dimensional space. This is due to the fact that stereoisomers are isomers because their atoms are different from others in terms of spatial arrangement.
Spatial Arrangement
First and foremost, one must understand the concept of spatial arrangement in order to understand stereoisomerism and chirality. Spatial arrangement of atoms concern how different atomic particles and molecules are situated about in the space around the organic compound, namely its carbon chain. In this sense, spatial arrangement of an organic molecule are different another if an atom is shifted in any three-dimensional direction by even one degree. This opens up a very broad possibility of different molecules, each with their unique placement of atoms in three-dimensional space .
Stereoisomers
Stereoisomers are, as mentioned above, different types of isomers within themselves, each with distinct characteristics that further separate them as different chemical entities having different properties. Types called enantiomers are the previously-mentioned mirror-image stereoisomers, and will be explained in detail in this article. Another type, a diastereomer, has different properties and will be introduced afterward.
Enantiomers
This type of stereoisomer is the essential mirror-image, non-superimposable type of stereoisomer introduced at the beginning of the article. Figure 2 provides a perfect example; note that the blue plane in the middle denotes the mirror plane.
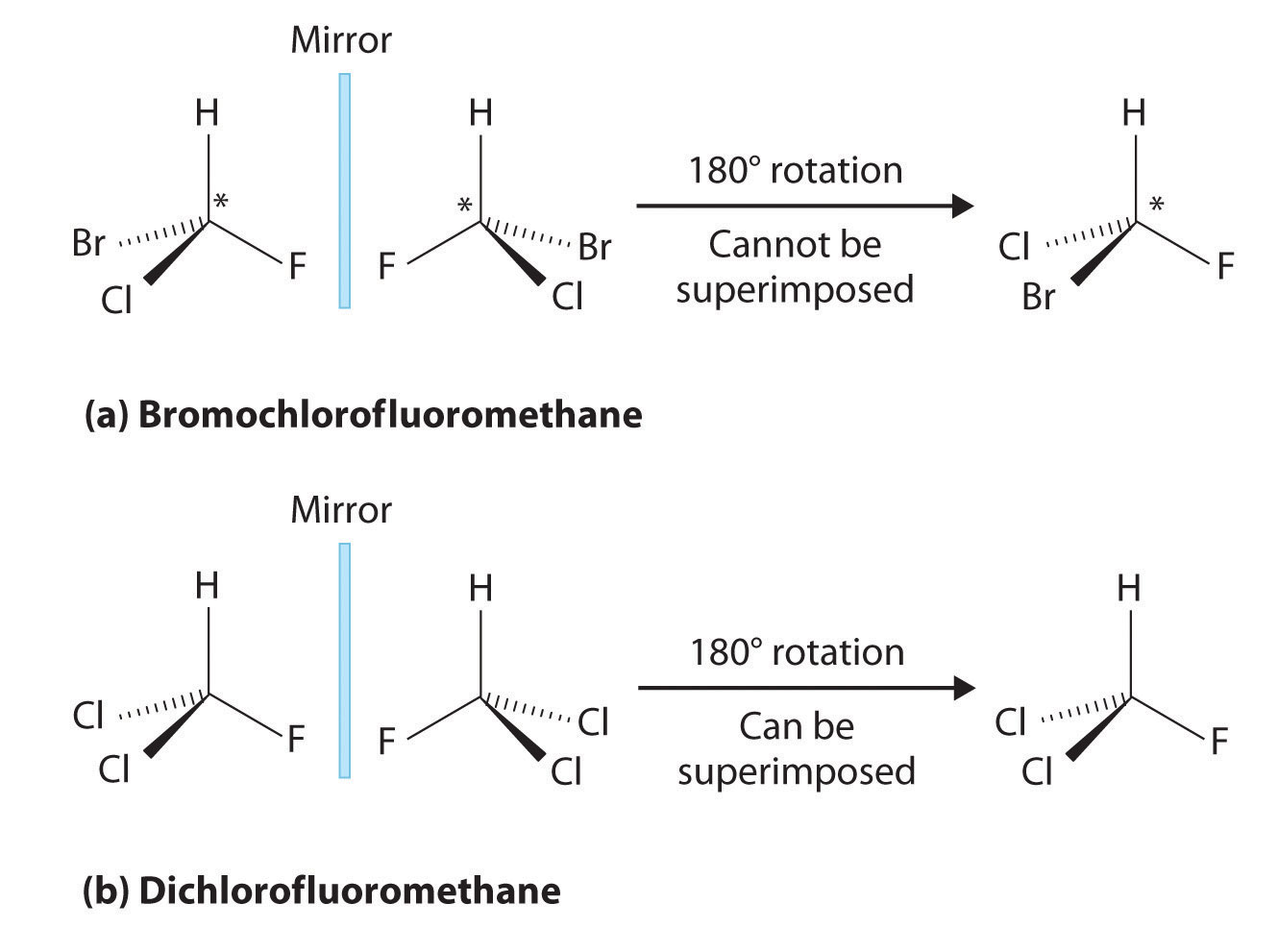
Note that even if one were to flip the left molecule over to the right, the atomic spatial arrangement will not be equal. This is equivalent to the left hand - right hand relationship, and is aptly referred to as 'handedness' in molecules. This can be somewhat counterintuitive, so this article recommends the reader try the 'hand' example. Place both palms facing up, and hands next to each other. Now flip either side over to the other. One hand should be showing the back of the hand, while the other shows the palm. They are not the same and non-superimposable.
This is where the concept of chirality comes in as one of the most essential and defining ideas of stereoisomerism.
Chirality
Chirality essentially means 'mirror-image, non-superimposable molecules', and to say that a molecule is chiral is to say that its mirror image (it must have one) is not the same as itself. Whether a molecule is chiral or achiral depends upon a certain set of overlapping conditions. Figure 2 shows examples of chiral and achiral molecules. Notice the distinct characteristic of the achiral molecule: it possesses two atoms of the same element. In theory and reality, if one were to create a plane that runs through the other two atoms, they will be able to create what is known as a bisecting plane: The images on either side of the plane are the same as the other (Figure 3).
In this case, the molecule is considered 'achiral'. In other words, to distinguish a chiral molecule from an achiral molecule, one must search for the existence of the bisecting plane in a molecule. All chiral molecules are deprived of a bisecting plane, whether simple or complex.
In general, no molecule with different surrounding atoms is achiral. Chirality is a simple but essential concept that supports the concept of stereoisomerism, used to explain one type of stereoisomer. The chemical properties of a chiral molecule differ from those of its mirror image, and this is the significance of chirality in modern organic chemistry.
Compounds with Multiple Chiral Centers
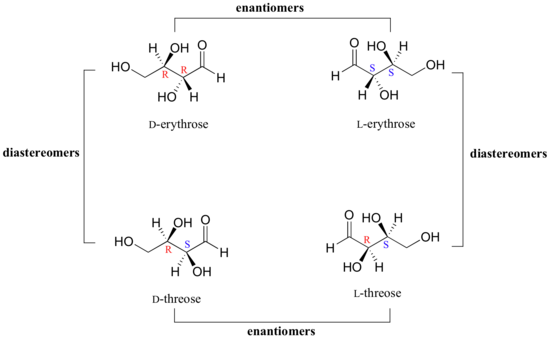
We turn our attention next to molecules which have more than one stereocenter. We will start with a common four-carbon sugar called D-erythrose.
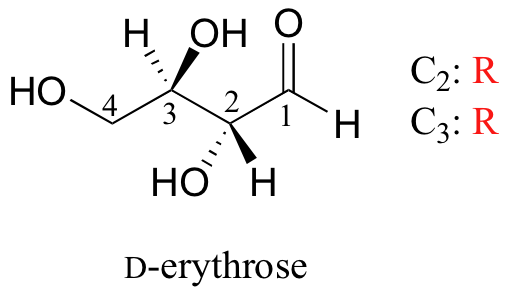
A note on sugar nomenclature: biochemists use a special system to refer to the stereochemistry of sugar molecules, employing names of historical origin in addition to the designators 'D' and 'L'. You will learn about this system if you take a biochemistry class. We will use the D/L designations here to refer to different sugars, but we won't worry about learning the system.
As you can see, D-erythrose is a chiral molecule: C2 and C3 are stereocenters, both of which have the R configuration. In addition, you should make a model to convince yourself that it is impossible to find a plane of symmetry through the molecule, regardless of the conformation. Does D-erythrose have an enantiomer? Of course it does – if it is a chiral molecule, it must. The enantiomer of erythrose is its mirror image, and is named L-erythrose (once again, you should use models to convince yourself that these mirror images of erythrose are not superimposable).
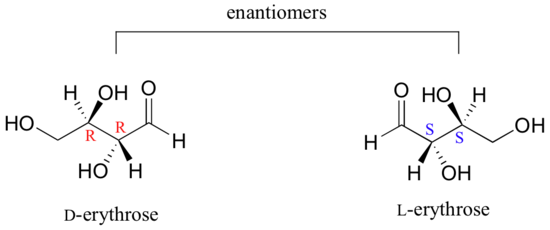
Notice that both chiral centers in L-erythrose both have the S configuration. In a pair of enantiomers, all of the chiral centers are of the opposite configuration.
What happens if we draw a stereoisomer of erythrose in which the configuration is S at C2 and R at C3? This stereoisomer, which is a sugar called D-threose, is not a mirror image of erythrose. D-threose is a diastereomer of both D-erythrose and L-erythrose.
The definition of diastereomers is simple: if two molecules are stereoisomers (same molecular formula, same connectivity, different arrangement of atoms in space) but are not enantiomers, then they are diastereomers by default. In practical terms, this means that at least one - but not all - of the chiral centers are opposite in a pair of diastereomers. By definition, two molecules that are diastereomers are not mirror images of each other.
L-threose, the enantiomer of D-threose, has the R configuration at C2 and the S configuration at C3. L-threose is a diastereomer of both erythrose enantiomers.
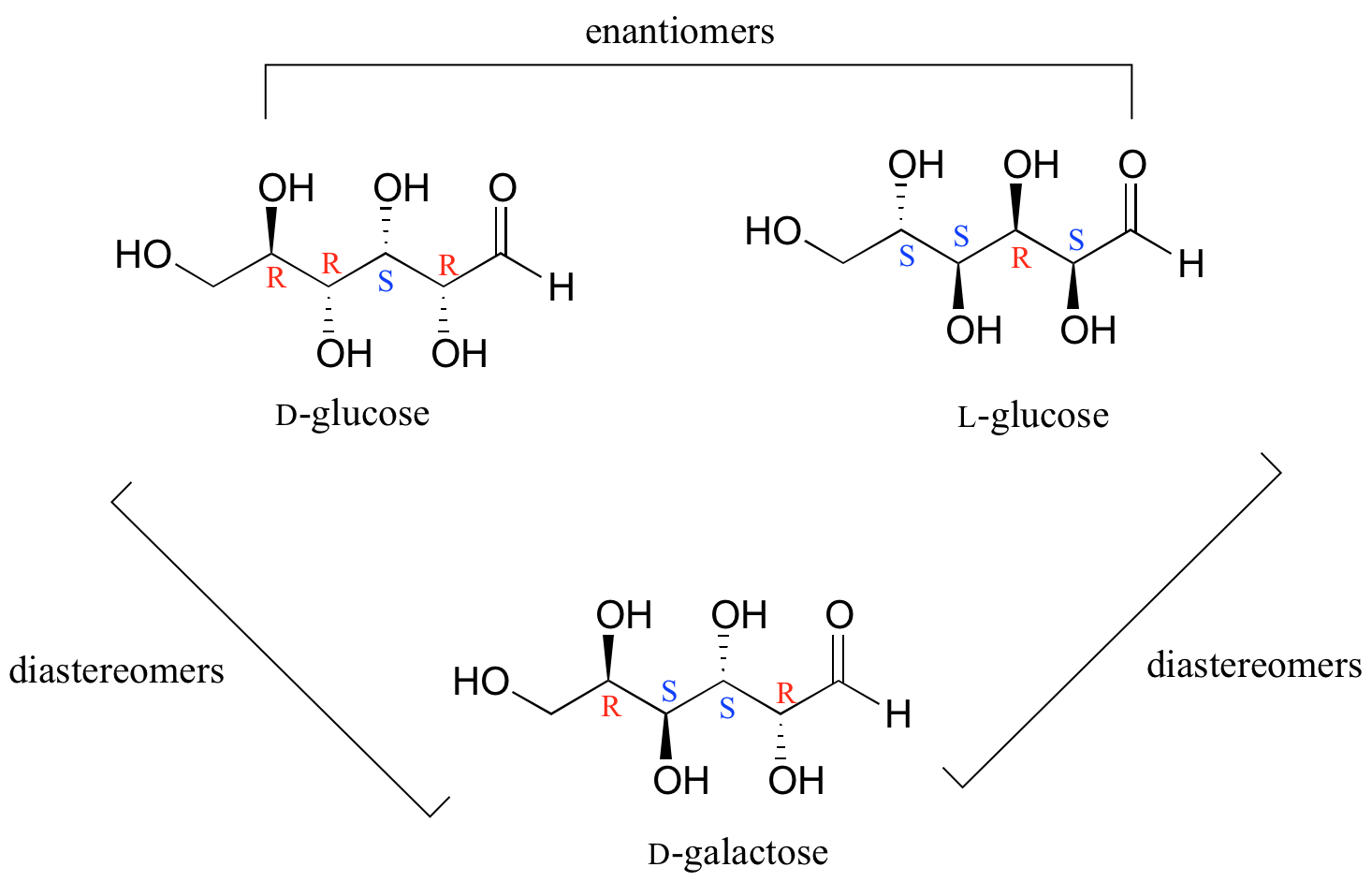
In general, a structure with n stereocenters will have 2n different stereoisomers. (We are not considering, for the time being, the stereochemistry of double bonds – that will come later). For example, let's consider the glucose molecule in its open-chain form (recall that many sugar molecules can exist in either an open-chain or a cyclic form). There are two enantiomers of glucose, called D-glucose and L-glucose. The D-enantiomer is the common sugar that our bodies use for energy. It has n = 4 stereocenters, so therefore there are 2n = 24 = 16 possible stereoisomers (including D-glucose itself).
In L-glucose, all of the stereocenters are inverted relative to D-glucose. That leaves 14 diastereomers of D-glucose: these are molecules in which at least one, but not all, of the stereocenters are inverted relative to D-glucose. One of these 14 diastereomers, a sugar called D-galactose, is shown above: in D-galactose, one of four stereocenters is inverted relative to D-glucose. Diastereomers which differ in only one stereocenter (out of two or more) are called epimers. D-glucose and D-galactose can therefore be refered to as epimers as well as diastereomers.
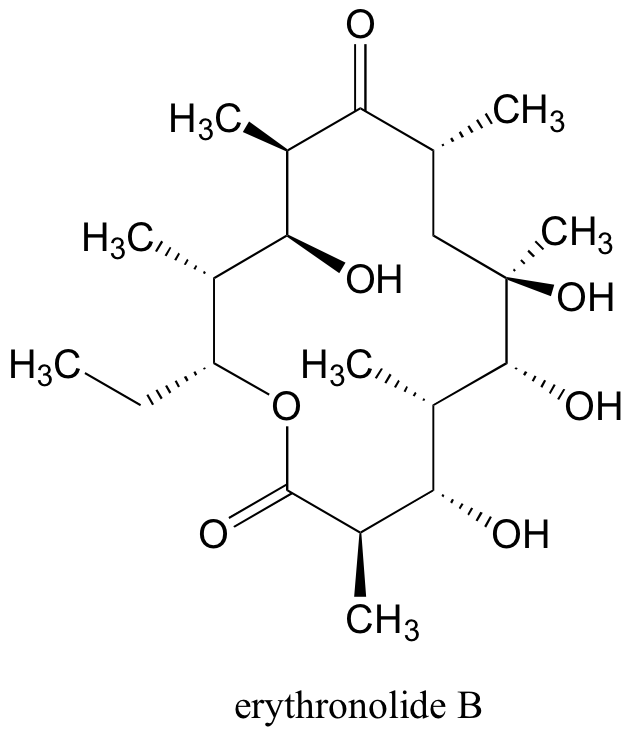
In total, there are 210 = 1024 stereoisomers in the erythronolide B family: 1022 of these are diastereomers of the structure above, one is the enantiomer of the structure above, and the last is the structure above.
We know that enantiomers have identical physical properties and equal but opposite degrees of specific rotation. Diastereomers, in theory at least, have different physical properties – we stipulate ‘in theory’ because sometimes the physical properties of two or more diastereomers are so similar that it is very difficult to separate them. In addition, the specific rotations of diastereomers are unrelated – they could be the same sign or opposite signs, and similar in magnitude or very dissimilar.
Constitutional isomers
Constitutional isomers, or structural isomers, are molecules with the same chemical formula but different atom and bond orientations. For example, both 3-methylpentane and hexane have the same chemical formula, C6H14, yet they clearly have different structures:
 |
 |
| 3-methylpentane | hexane |
Another example involves functional groups. Methoxy methane, an ether, and ethanol, an alcohol, both have the chemical formula C2H6O:
 |
 |
| Methoxy methane | Ethanol |
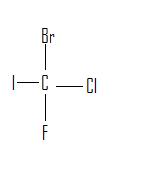
Identify the following as either a constitutional isomer or stereoisomer. If stereoisomer, determine if it is an enantiomer or diastereomer. Explain the reason behind the answer. Also mark chirality for each molecule.
1.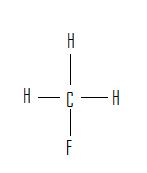 2.
2.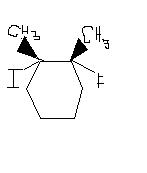 3.
3.
References
- Anslyn, Eric V. and Dougherty, Dennis A. Modern Physical Organic Chemistry. Chicago, IL.: University Science. 2005
- Hick, Janice M. The Physical Chemistry of Chirality. New York, N.Y.: An American Chemical Society Publication. 2001.
- Vollhardt, K. Peter C. and Schore, Neil E. Organic Chemistry: Structure and Function. Fifth Edition. New York, N.Y.: W. H. Freeman Company, 2007.
Section 4.1.1 Stereoisomers and Chiral Centers
We turn now to concept of chirality that formed the basis of the story about Louis Pasteur in the beginning of this chapter. Recall that the term chiral, from the Greek work for 'hand', refers to anything which cannot be superimposed on its own mirror image. Your hands, of course, are chiral - you cannot superimpose your left hand on your right, and you cannot fit your left hand into a right-handed glove (which is also a chiral object). Another way of saying this is that your hands do not have a mirror plane of symmetry: you cannot find any plane which bisects your hand in such a way that one side of the plane is a mirror image of the other side. Chiral objects do not have a plane of symmetry.
Your face, on the other hand is achiral - lacking chirality - because, some small deviations notwithstanding, you could superimpose your face onto its mirror image. If someone were to show you a mirror image photograph of your face, you could line the image up, point-for-point, with your actual face. Your face has a plane of symmetry, because the left side is the mirror image of the right side.
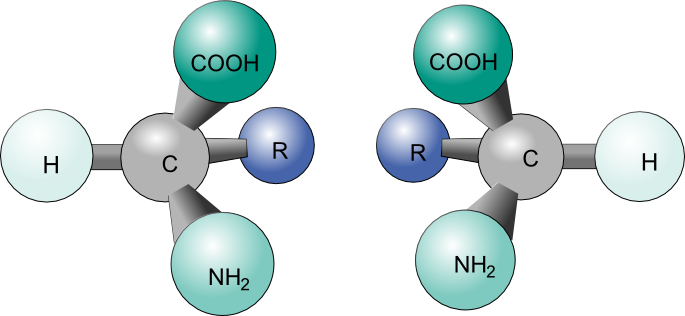
What Pasteur, Biot, and their contemporaries did not yet fully understand when Pasteur made his discovery of molecular chirality was the source of chirality at the molecular level. It stood to reason that a chiral molecule is one that does not contain a plane of symmetry, and thus cannot be superimposed on its mirror image. We now know that chiral molecules contain one or more chiral centers, which are almost always tetrahedral (sp3-hybridized) carbons with four different substituents. Consider the cartoon molecule A below: a tetrahedral carbon, with four different substituents denoted by balls of four different colors (for the time being, don't worry about exactly what these substituents could be - we will see real examples very soon).
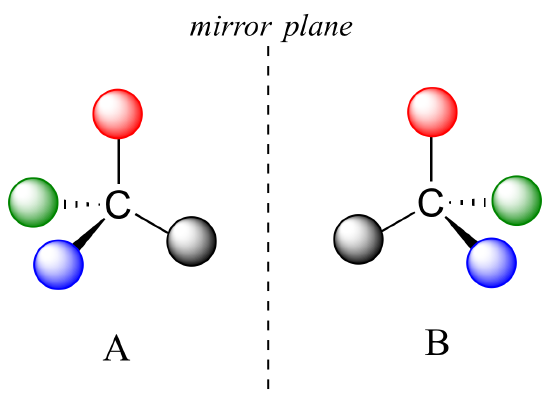
The mirror image of A, which we will call B, is drawn on the right side of the figure, and an imaginary mirror is in the middle. Notice that every point on A lines up through the mirror with the same point on B: in other words, if A looked in the mirror, it would see B looking back.
Now, if we flip compound A over and try to superimpose it point for point on compound B, we find that we cannot do it: if we superimpose any two colored balls, then the other two are misaligned.
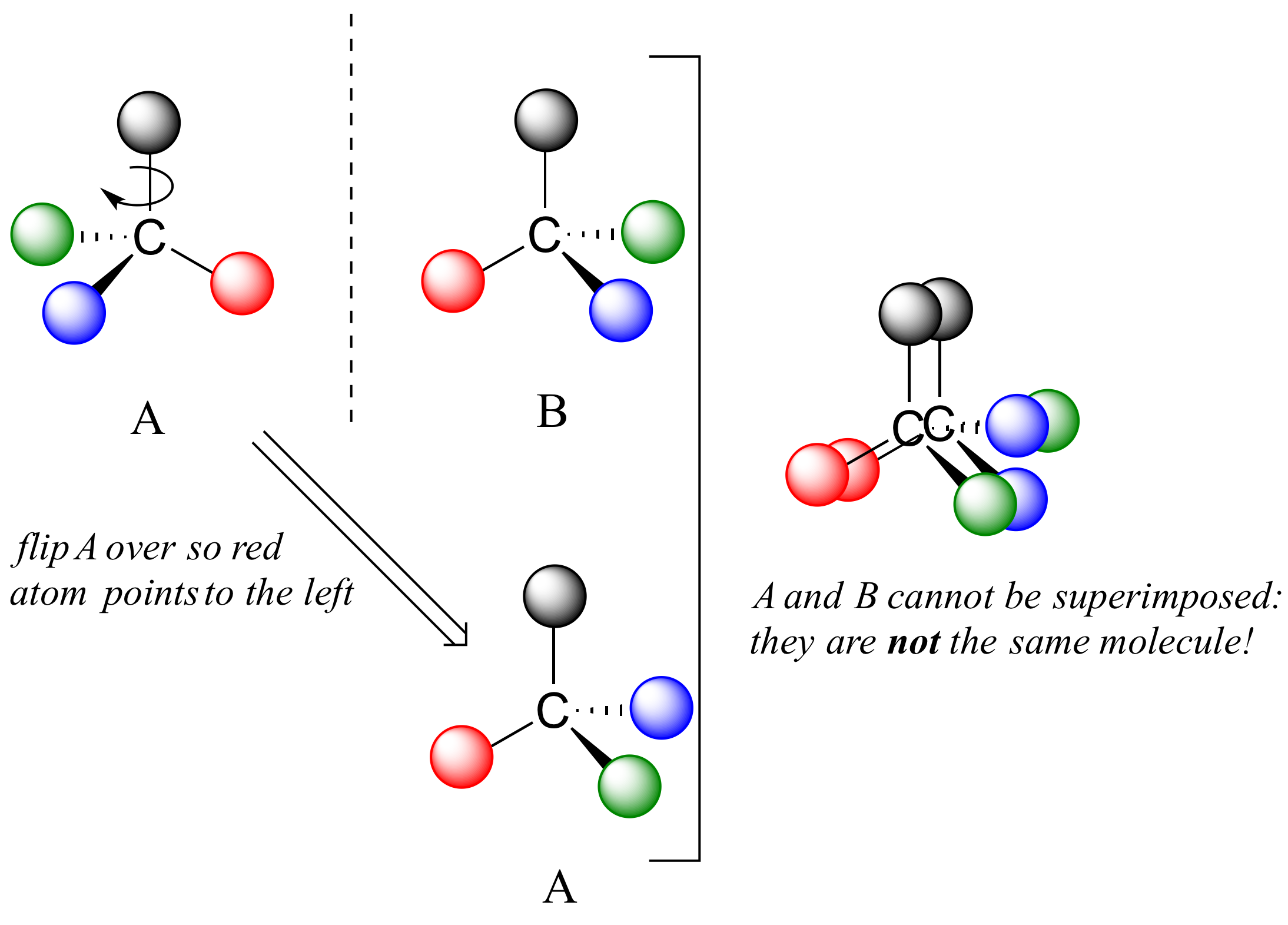
A is not superimposable on its mirror image (B), thus by definition A is a chiral molecule. It follows that B also is not superimposable on its mirror image (A), and thus it is also a chiral molecule. Also notice in the figure below (and convince yourself with models) that neither A nor B has an internal plane of symmetry.
A and B are stereoisomers: molecules with the same molecular formula and the same bonding arrangement, but a different arrangement of atoms in space. There are two types of stereoisomers: enantiomers and diastereomers. Enantiomers are pairs of stereoisomers which are mirror images of each other: thus, A and B are enantiomers. It should be self-evident that a chiral molecule will always have one (and only one) enantiomer: enantiomers come in pairs. Enantiomers have identical physical properties (melting point, boiling point, density, and so on). However, enantiomers do differ in how they interact with polarized light (we will learn more about this soon) and they may also interact in very different ways with other chiral molecules - proteins, for example. We will begin to explore this last idea in later in this chapter, and see many examples throughout the remainder of our study of biological organic chemistry.
Diastereomers are stereoisomers which are not mirror images of each other. For now, we will concentrate on understanding enantiomers, and come back to diastereomers later.
We defined a chiral center as a tetrahedral carbon with four different substituents. If, instead, a tetrahedral carbon has two identical substituents (two black atoms in the cartoon figure below), then of course it still has a mirror image (everything has a mirror image, unless we are talking about a vampire!) However, it is superimposable on its mirror image, and has a plane of symmetry.
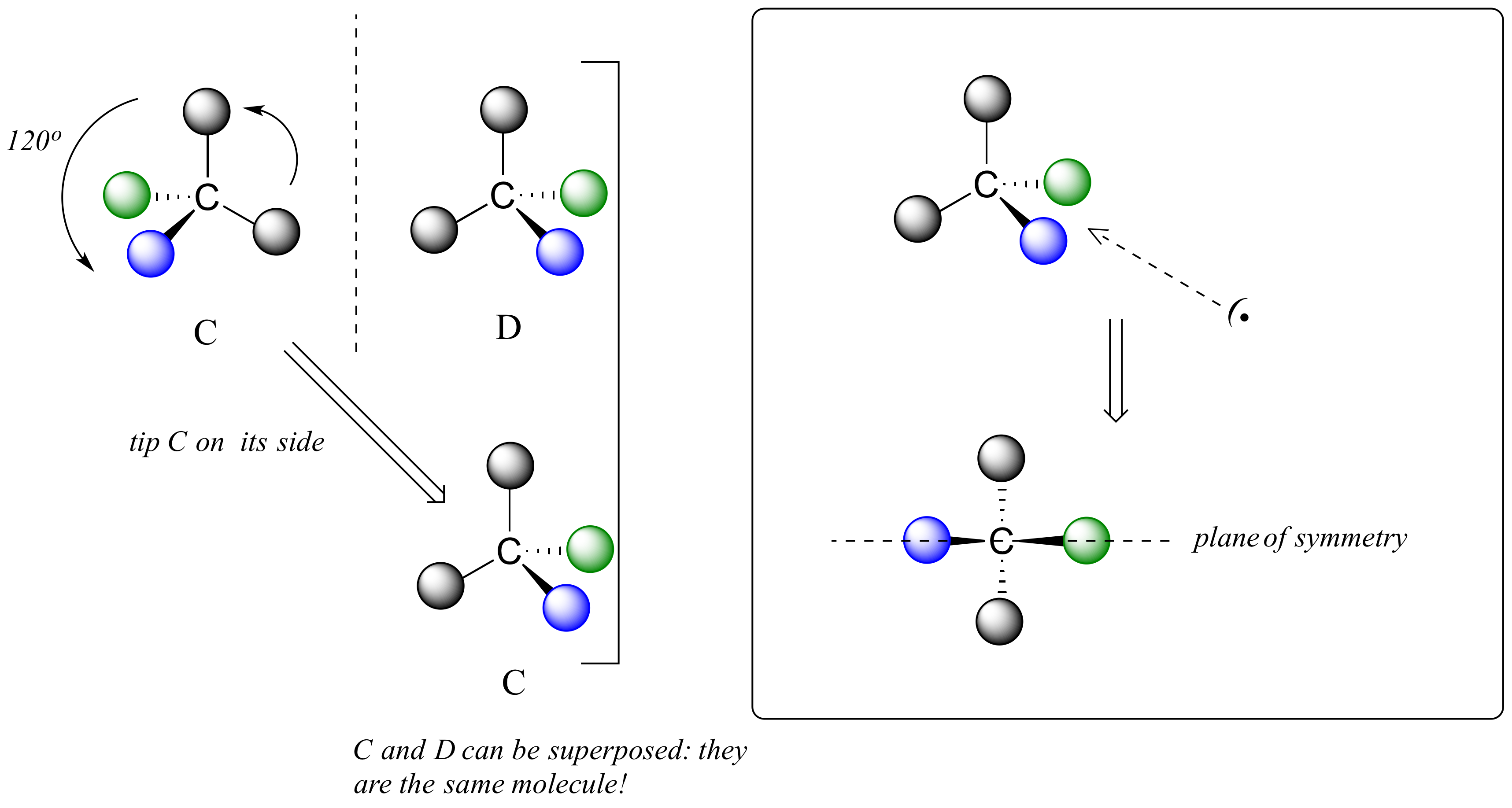
This molecule is achiral (lacking chirality). Using the same reasoning, we can see that a trigonal planar (sp2-hybridized) carbon is also not a chiral center.
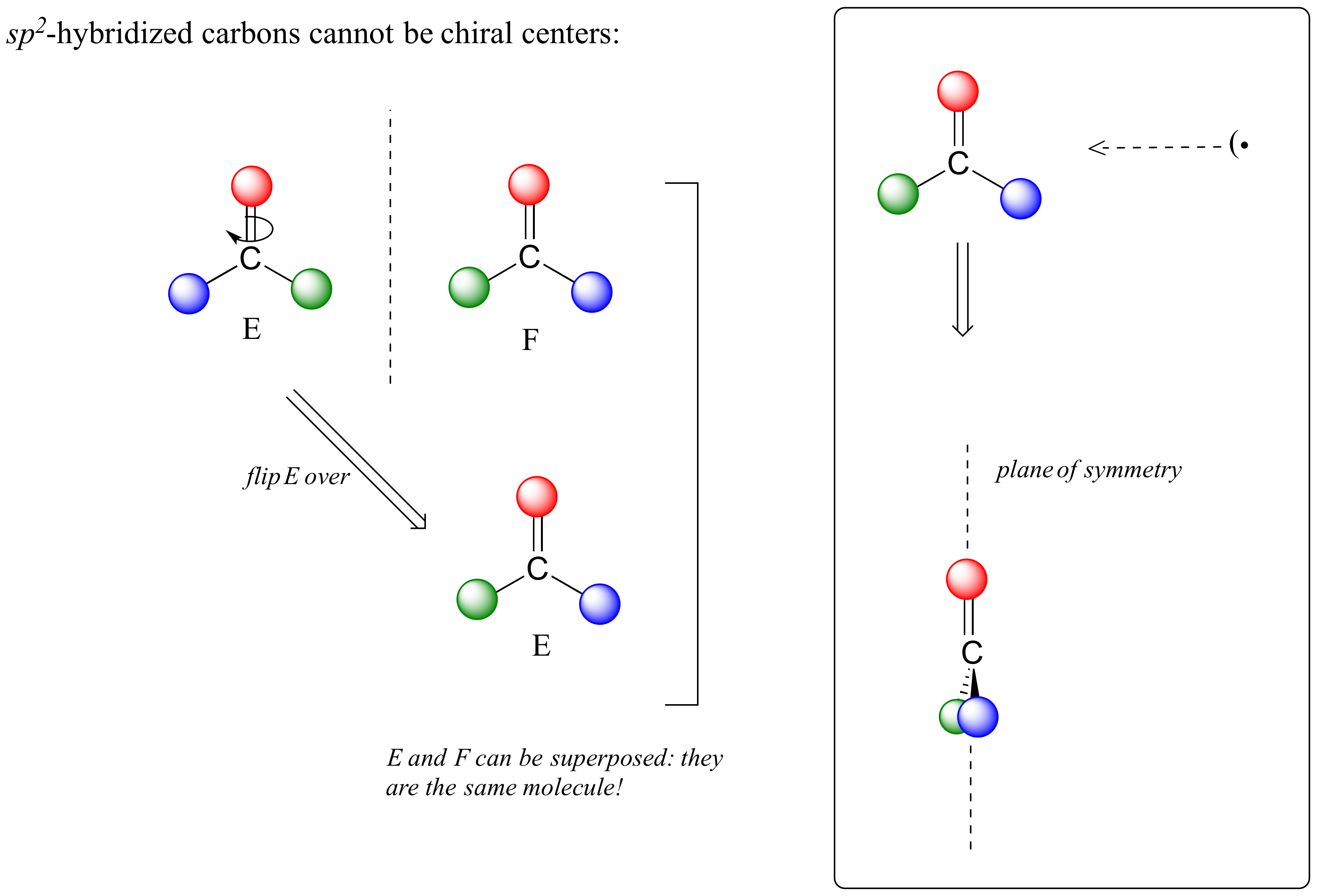
Notice that structure E can be superimposed on F, its mirror image - all you have to do is pick E up, flip it over, and it is the same as F. This molecule has a plane of symmetry, and is achiral.
Let's apply our general discussion to real molecules. For now, we will limit our discussion to molecules with a single chiral center. It turns out that tartaric acid, the subject of our chapter introduction, has two chiral centers, so we will come back to it later.
Consider 2-butanol, drawn in two dimensions below.
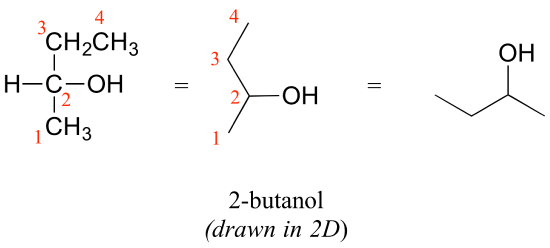
Carbon #2 is a chiral center: it is sp3-hybridized and tetrahedral (even though it is not drawn that way above), and the four things attached to is are different: a hydrogen, a methyl (-CH3) group, an ethyl (-CH2CH3) group, and a hydroxyl (OH) group. Let's draw the bonding at C2 in three dimensions, and call this structure A. We will also draw the mirror image of A, and call this structure B.
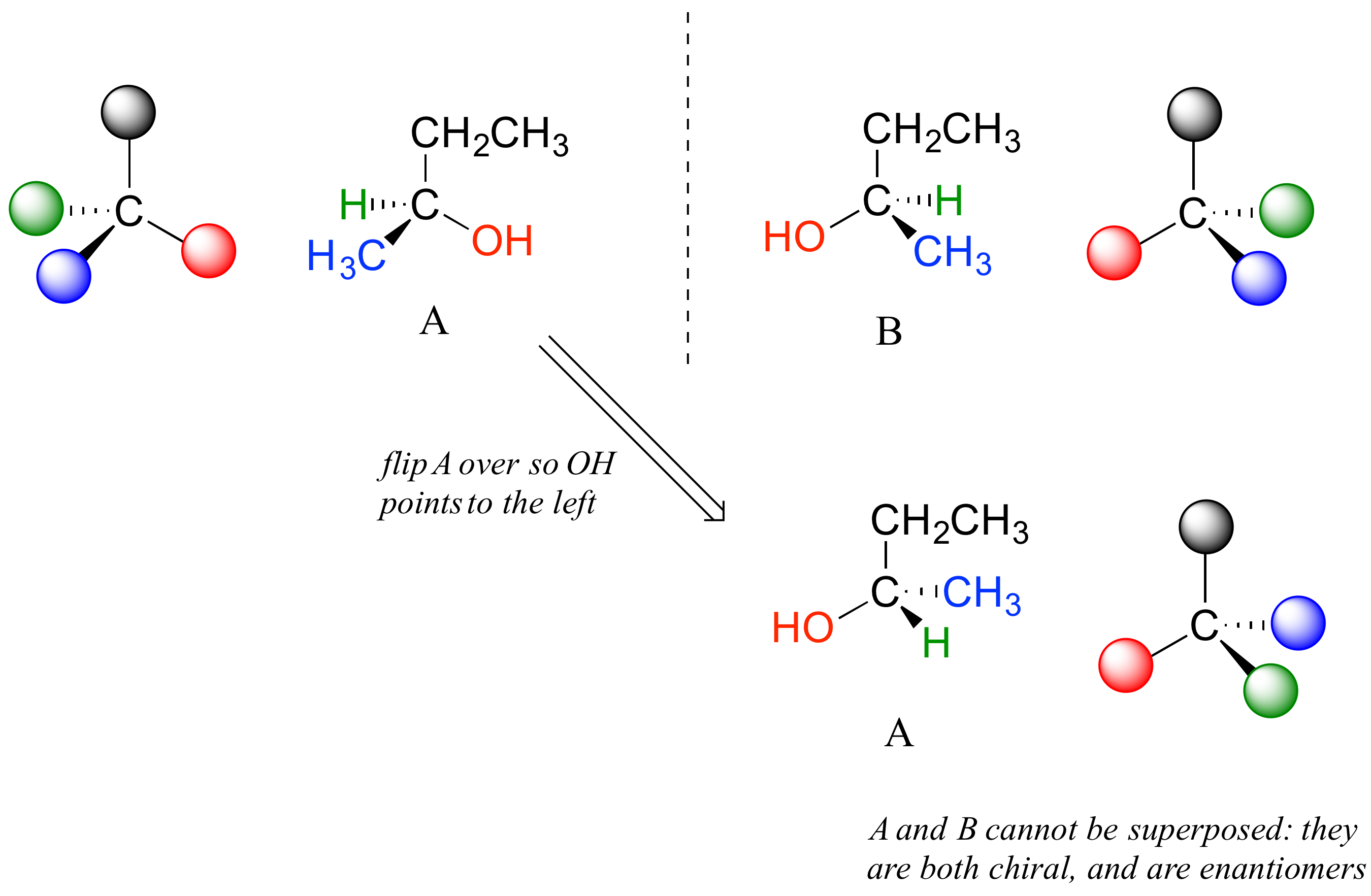
When we try to superimpose A onto B, we find that we cannot do it. A and B are both chiral molecules, and they are enantiomers of each other.
2-propanol, unlike 2-butanol, is not a chiral molecule. Carbon #2 is bonded to two identical substituents (methyl groups), and so it is not a chiral center.
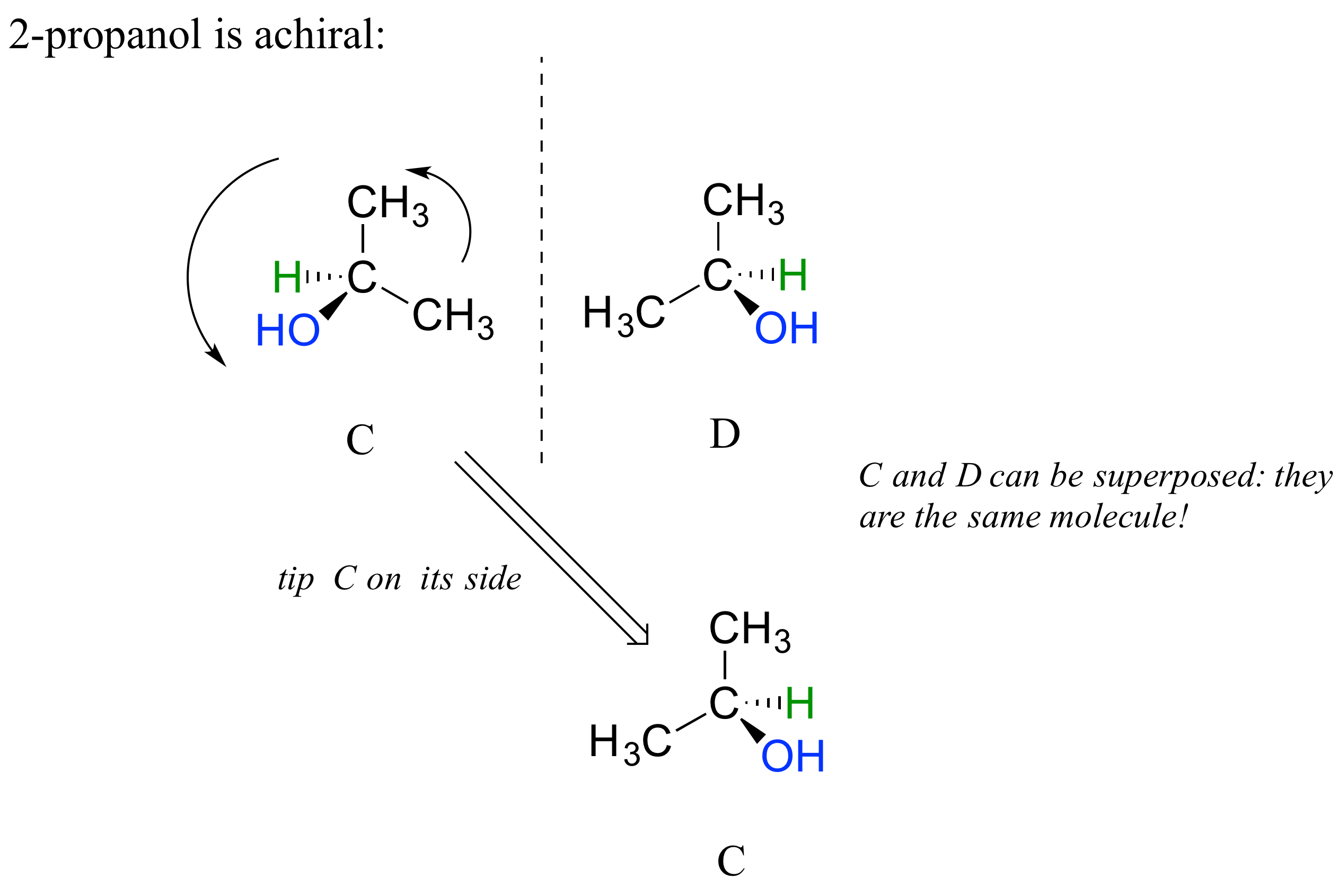
Notice that 2-propanol is superimposable on its own mirror image.
When we look at very simple molecules like 2-butanol, it is not difficult to draw out the mirror image and recognize that it is not superimposable. However, with larger, more complex molecules, this can be a daunting challenge in terms of drawing and three-dimensional visualization. The easy way to determine if a molecule is chiral is simply to look for the presence of one or more chiral centers: molecules with chiral centers will (almost always) be chiral. We insert the 'almost always' caveat here because it is possible to come up with the exception to this rule - we will have more to say on this later, but don't worry about it for now.
Here's another trick to make your stereochemical life easier: if you want to draw the enantiomer of a chiral molecule, it is not necessary to go to the trouble of drawing the point-for-point mirror image, as we have done up to now for purposes of illustration. Instead, keep the carbon skeleton the same, and simply reverse the solid and dashed wedge bonds on the chiral carbon: that accomplishes the same thing. You should use models to convince yourself that this is true, and also to convince yourself that swapping any two substituents about the chiral carbon will result in the formation of the enantiomer.
Here are four more examples of chiral biomolecules, each one shown as a pair of enantiomers, with chiral centers marked by red dots.
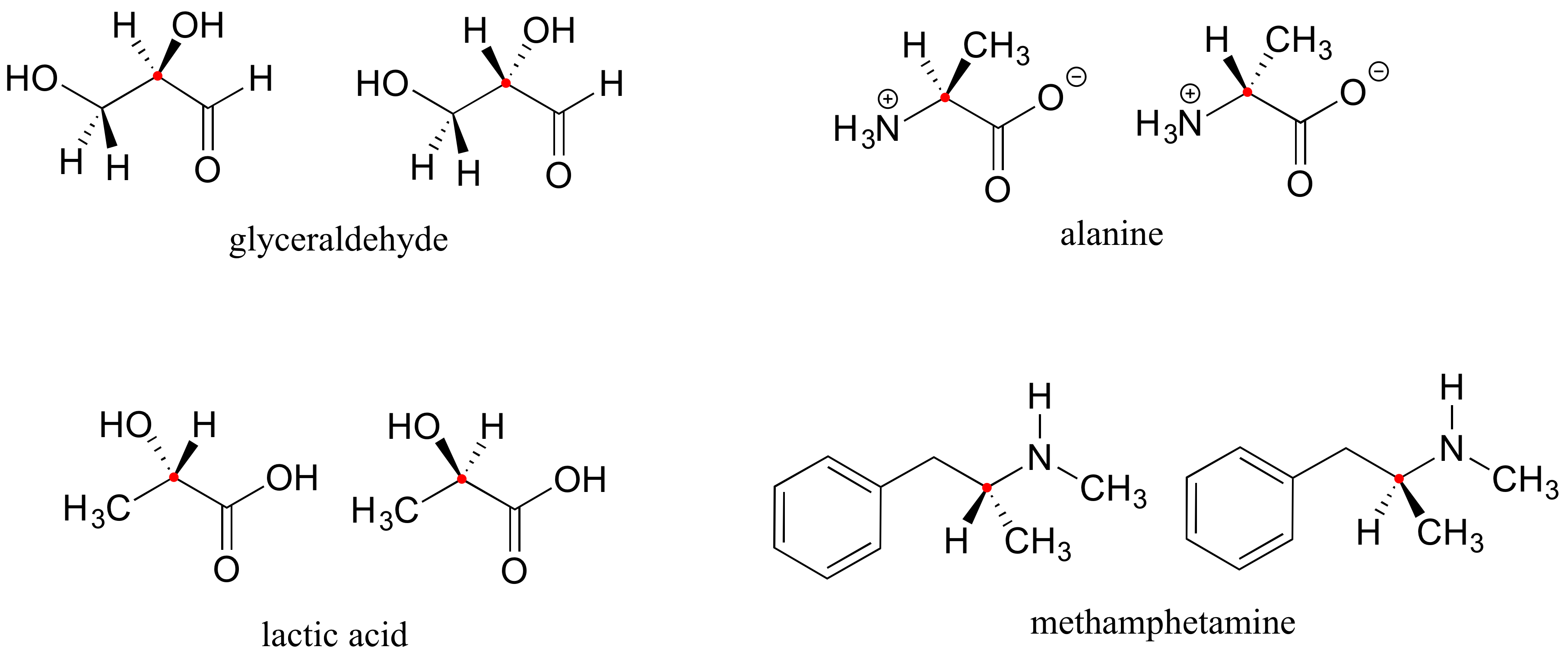
Here are some examples of achiral biomolecules - convince yourself that none of them contain a chiral center:
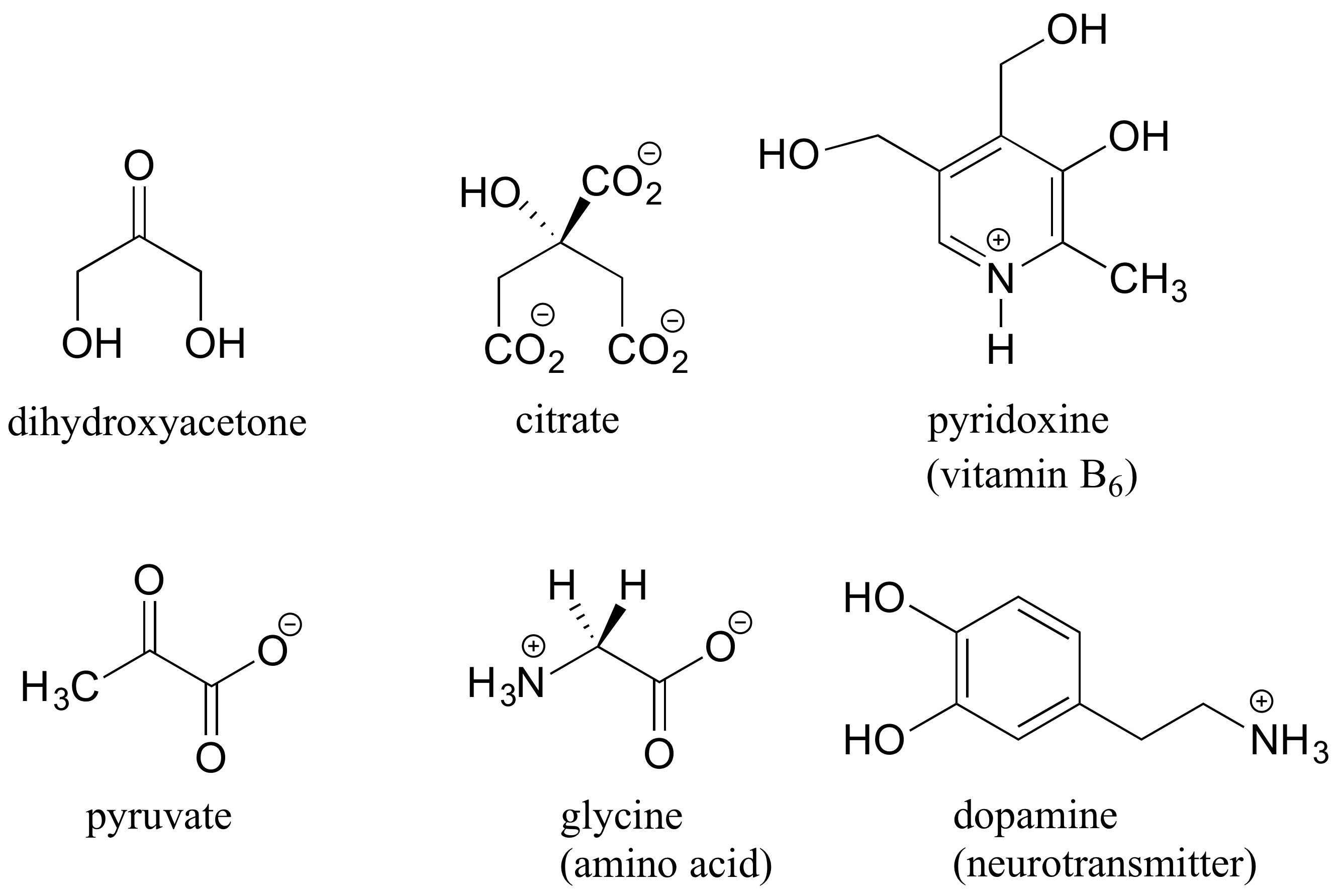
When looking for chiral centers, it is important to recognize that the question of whether or not the dashed/solid wedge drawing convention is used is irrelevant. Chiral molecules are sometimes drawn without using wedges (although obviously this means that stereochemical information is being omitted). Conversely, wedges may be used on carbons that are not chiral centers – look, for example, at the drawings of glycine and citrate in the figure above.
Can a chiral center be something other than a tetrahedral carbon with four different substituents? The answer to this question is 'yes' - however, these alternative chiral centers are very rare in the context of biological organic chemistry, and outside the scope of our discussion here.
You may also have wondered about amines: shouldn't we consider a secondary or tertiary amine to be a chiral center, as they are tetrahedral and attached to four different substituents, if the lone-pair electrons are counted as a 'substituent'? Put another way, isn't an amine non-superimposable on its mirror image?
The answer: yes it is, in the static picture, but in reality, the nitrogen of an amine is rapidly and reversibly inverting, or turning inside out, at room temperature.

If you have trouble picturing this, take an old tennis ball and cut it in half. Then, take one of the concave halves and flip it inside out, then back again: this is what the amine is doing. The end result is that the two 'enantiomers' if the amine are actually two rapidly interconverting forms of the same molecule, and thus the amine itself is not a chiral center. This inversion process does not take place on a tetrahedral carbon, which of course has no lone-pair electrons.
Exercise 3.8: Locate all of the chiral centers (there may be more than one in a molecule). Remember, hydrogen atoms bonded to carbon usually are not drawn in the line structure convention - but they are still there!
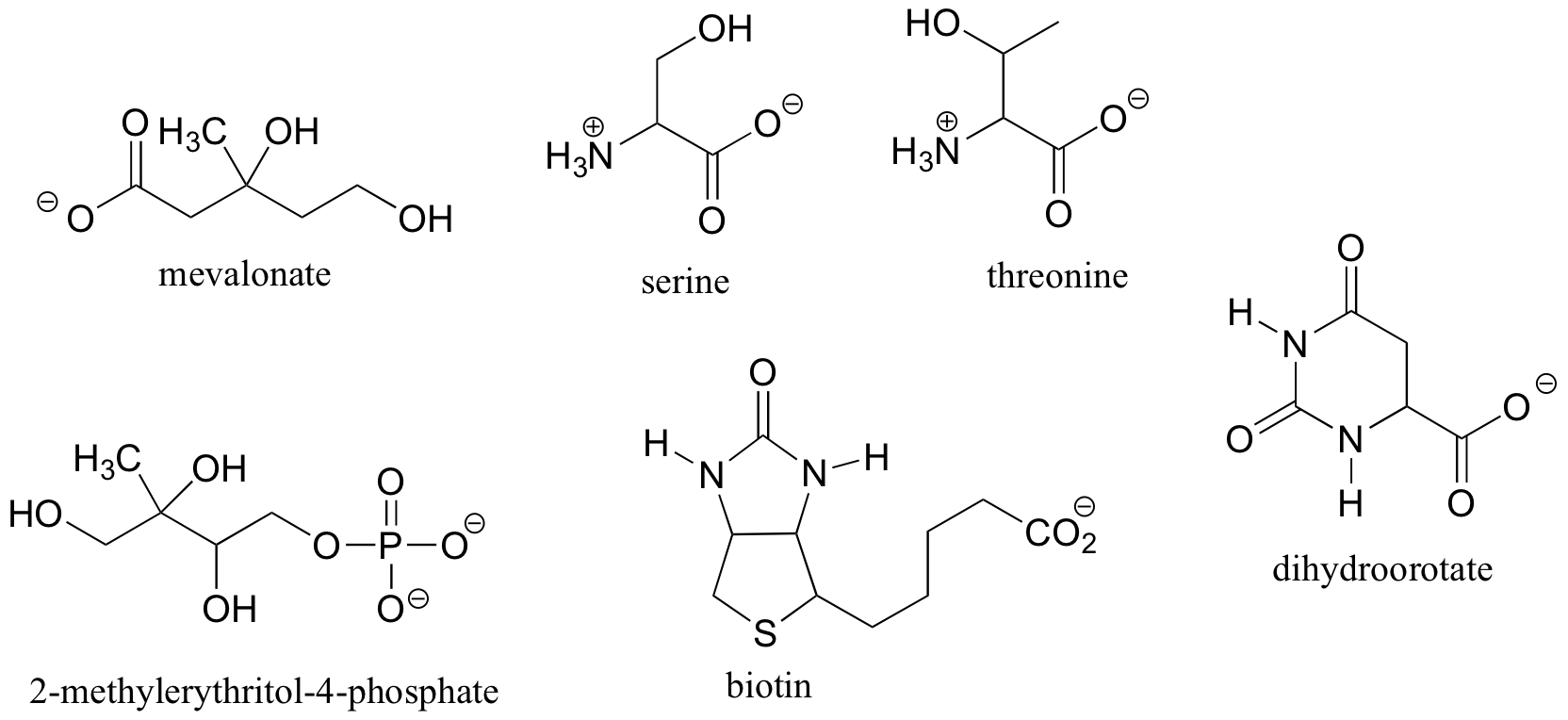
Exercise 3.9:
a) Draw two enantiomers of i) mevalonate and ii) serine.
b) Are the two 2-butanol structures below enantiomers?

Exercise 3.10: Label the molecules below as chiral or achiral, and locate all chiral centers.
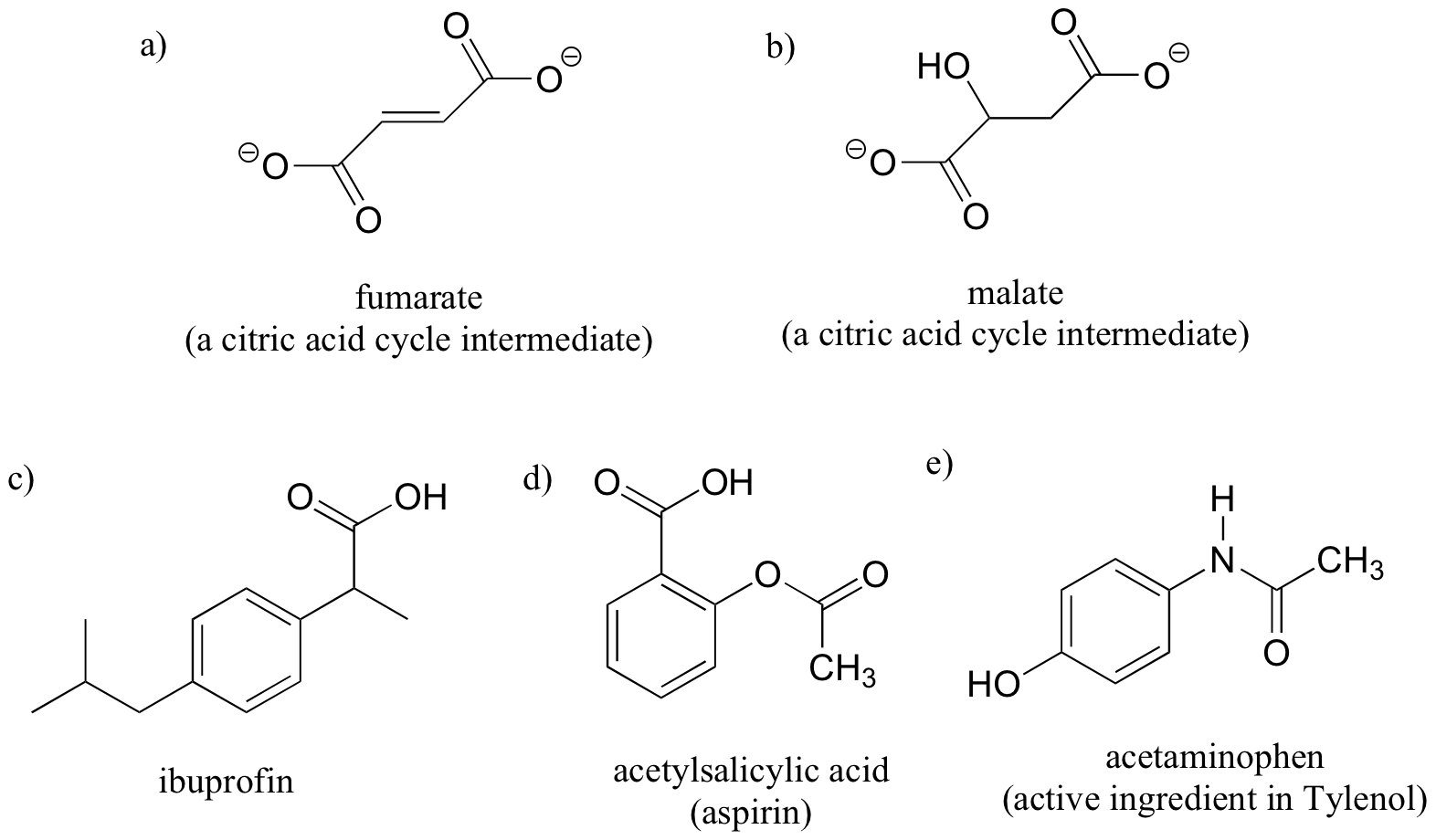
Kahn Academy video tutorials
Chirality
Enantiomers
Further Reading on Chirality
Khan Academy
Cliffs Notes
Web Pages
Other Resources
Practice Problems
Principles of Chirality Problems
Further Reading on Stereoisomers and Chiral Centers
MasterOrganicChemistry
Carey 4th Edition On-Line Activity
Carbon-based Stereogenic Centers
Stereogenic Centers Other than Carbon
Khan Academy
Chirality Centers and Stereoisomers
Cliffs Notes
Web Pages
Tutorial
Other Resources