9.1: First Order Eliminations

Recall the S_N1 reaction that occurs between alcohols and hydrogen halides. The first step in the reaction involves protonation of the alcohol to form an oxonium ion. We say that H₂O will leave (pK_a < 4) to generate a carbocation. At this point, we said that if there was a halide ion in the mixture, it would react to give an alkyl halide. This assumes that the halide ion is sufficiently reactive enough to form that \(σ_{C-X}\) bond. What would happen if the anion wasn’t very nucleophilic?

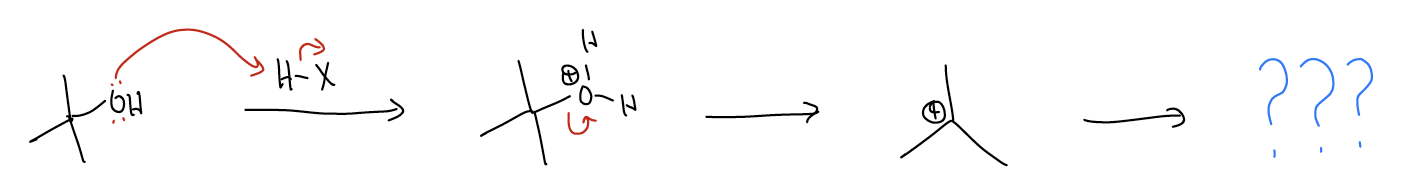
In this case, the carbocation would still form, but would react via a different set of curly arrows to give a different product. We call this reaction an elimination reaction because H₂O is eliminated to give an alkene.

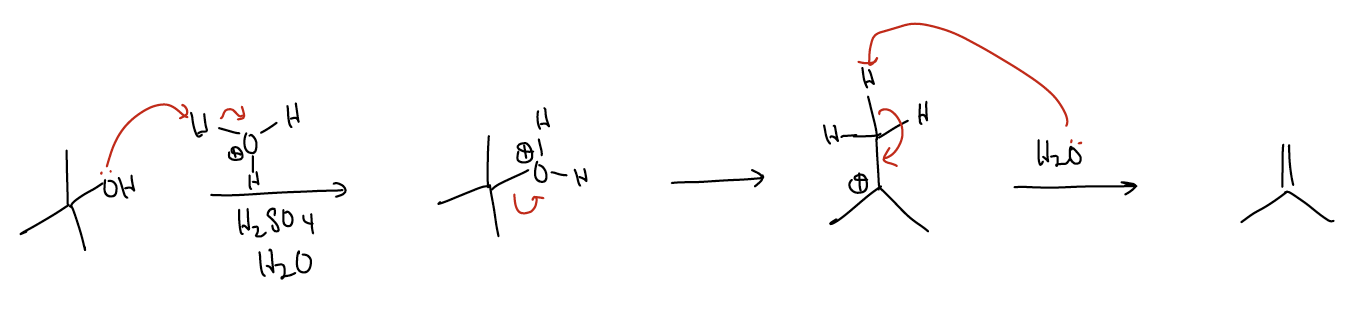
Here, sulfuric acid acts as the proton source, but the hydrogen sulfate anion is too weak of a nucleophile to form a \(σ_{C-O}\) bond. Instead, H₂O acts as a base rather than a nucleophile and deprotonates an acidic proton, placing its electrons into a newly formed \(π_{C-C}\) bond. This reaction is called an E₁ reaction. Much like the S_N1 reaction, the rate-determining step is the formation of the carbocation.

Let’s view this reaction from the perspective of a Newman projection:

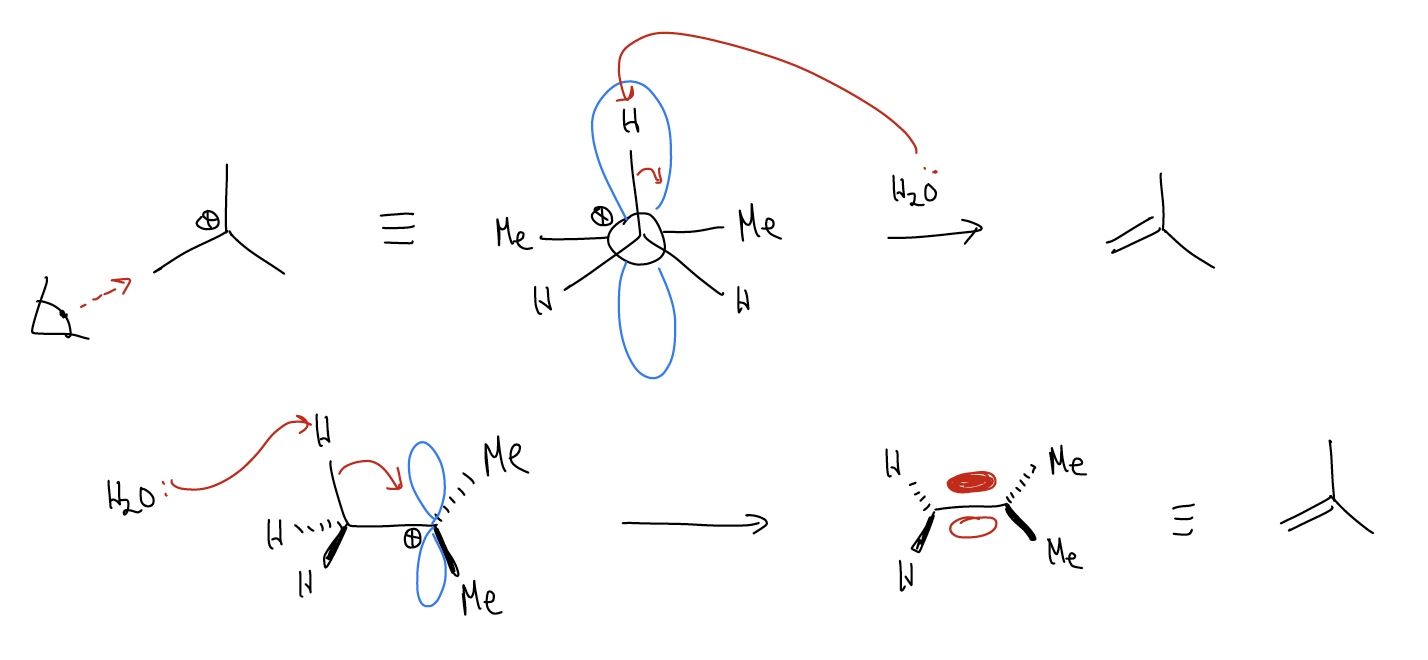
The \(σ_{C-H}\) bond is perfectly aligned with the two lobes of the atomic p orbital so that upon deprotonation, the electrons can overlap with the empty atomic p orbital and form a new \(π_{C-C}\) bond. Thus, in order for an E₁ reaction to occur, a \(σ_{C-H}\) bond must be able to overlap with an atomic p orbital. The conformation of a molecule must allow this (\(σ_{C-C}\) and \(σ_{C-X}\) will not eliminate). Let’s look at a few examples:

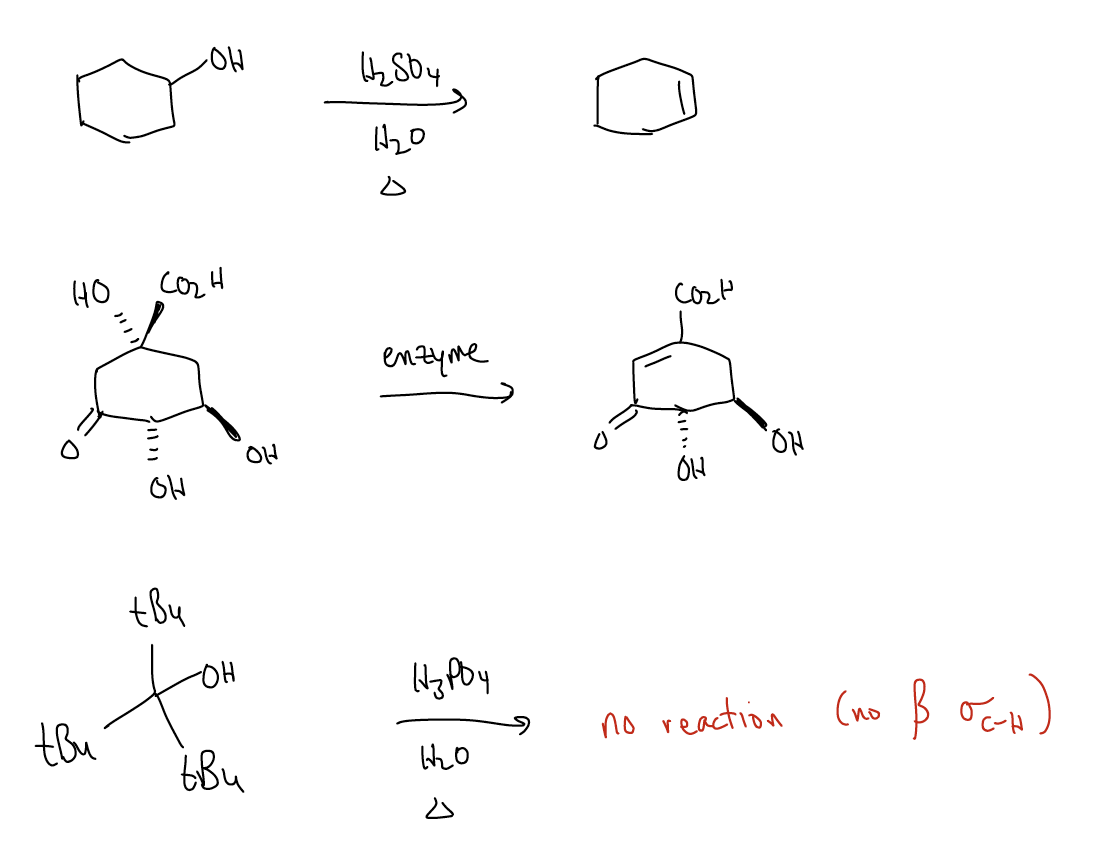
This might sound pretty straightforward, but there are two things that we need to worry about in an E₁ reaction:

1. Regioselectivity – if there is more than one functional group that can react, we must ask ourselves which one will react. This is the regiochemistry of the reaction. If one regioisomer forms predominantly, we sat that the reaction is regioselective. In the case of the E₁ reaction, say that you have several \(σ_{C-H}\) bonds that overlap with the empty atomic p orbital. How do you know which one to deprotonate? Deprotonation to give the more highly substituted alkene product of an E₁ reaction will generate the Zaitsev product, while deprotonation to give the less highly substituted alkene product will generate the Hoffman product. Zaitsev’s rule states that the more highly substituted alkene will form predominantly. There are ways to favor the Hoffman product, which we will encounter later.

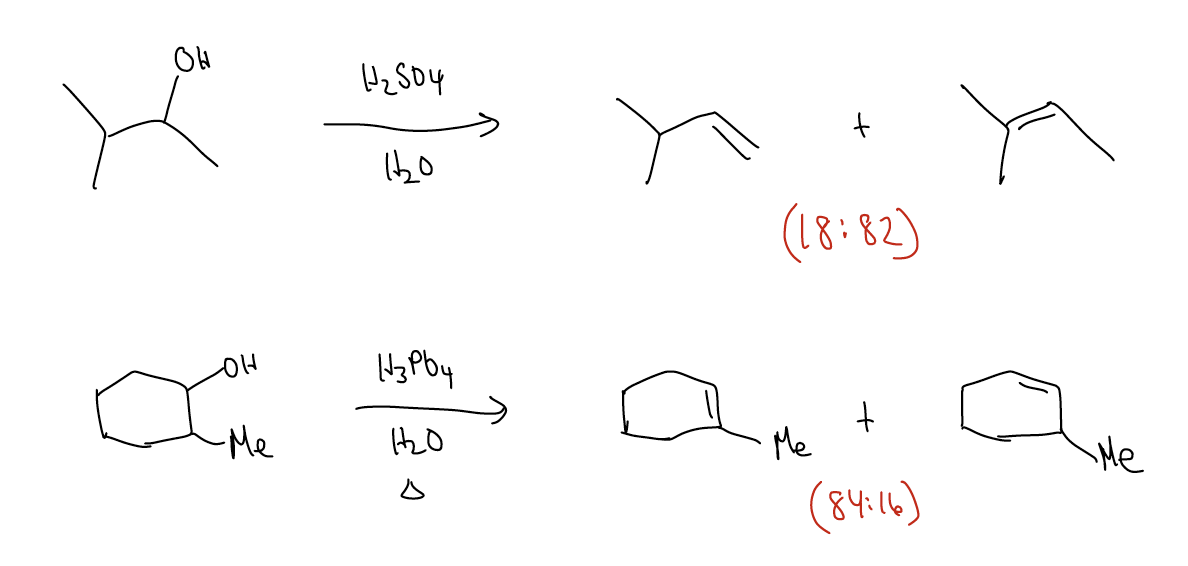
Zaitsev’s rule occurs because the transition state energy is stabilized (lower) due to an increase in \(σ\)-donation, even if statistically there are fewer \(σ_{C-H}\) bonds. This means that the regiochemistry-inducing step is under kinetic control – the height of the transition state is more important. It just so happens that the thermodynamically more stable product (think, more highly substituted alkene) also forms. But remember that thermodynamics and kinetics are different things.

2. Stereoselectivity – if more than one stereoisomer can be produced in a reaction, we must ask ourselves which one will be the major product. It is possible that deprotonating a single proton in an E₁ reaction could give more than one product that are themselves geometric isomers (diastereomers).

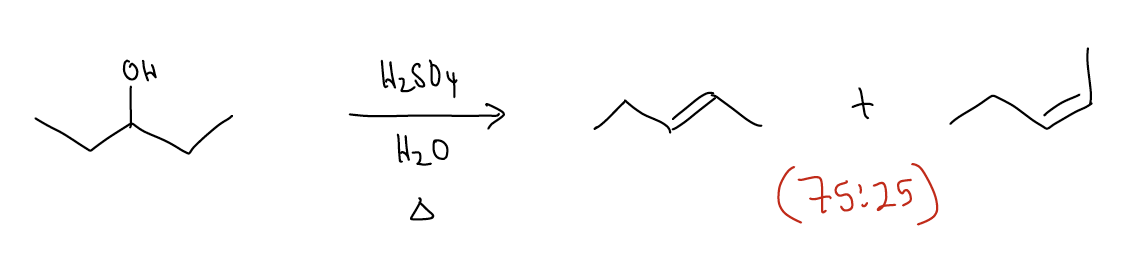
We can rationalize the selectivity by looking at the mechanism. Let’s skip forward to the formation of the carbocation, which is the rate-determining step. Everything thereafter is fast, but the energy of the transition state will determine which stereoisomer you get. Therefore, the deprotonation is also the stereochemistry-inducing step. There are two different conformations which have overlap between a \(σ_{C-H}\) and the atomic p orbital. Deprotonation of these hydrogens will give either the E or Z-alkene. One conformation has a gauche interaction which increases the energy of the transition state because of steric strain. This would be the unflavored deprotonation leading to the Z-alkene. In the other conformation, the two biggest groups are on opposite sides, so this would lead to the E-alkene. Again, the stereochemistry is controlled by the energy of the transition state (kinetic control), but happens to lead to the more stable product.

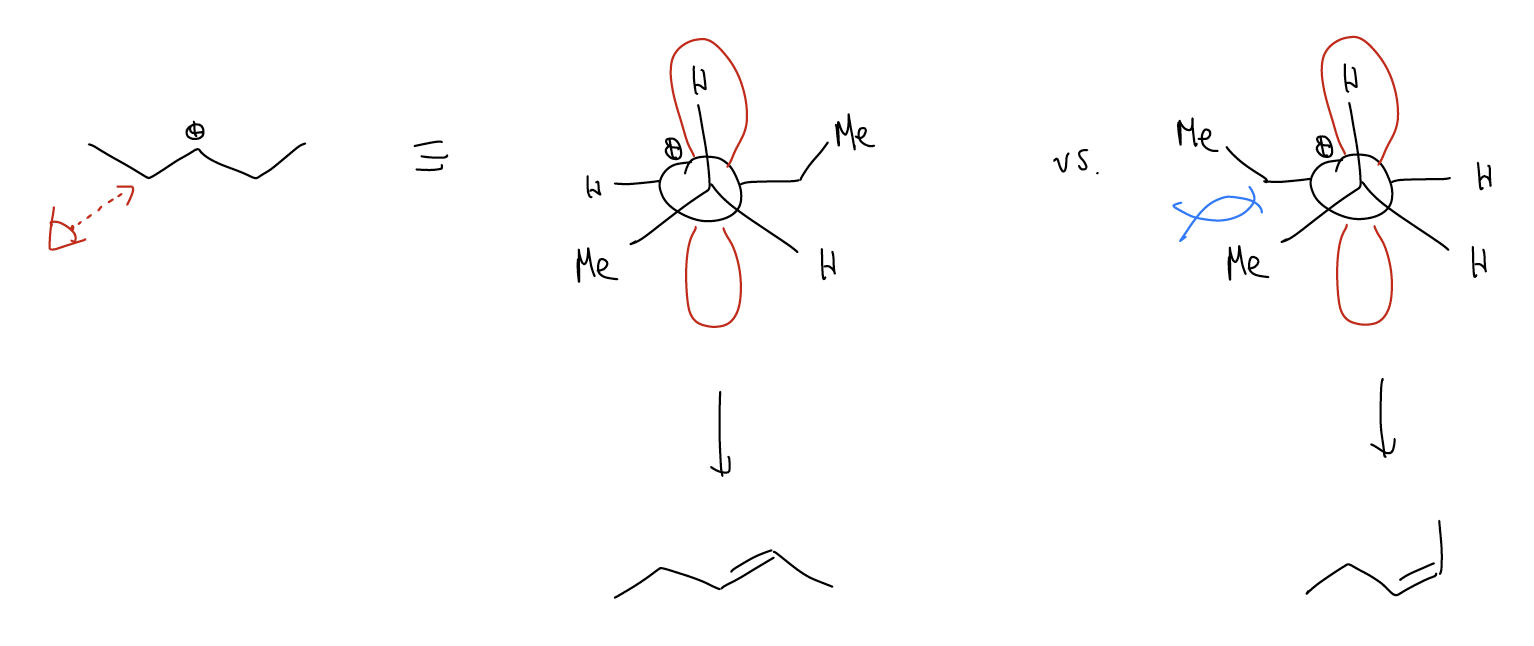
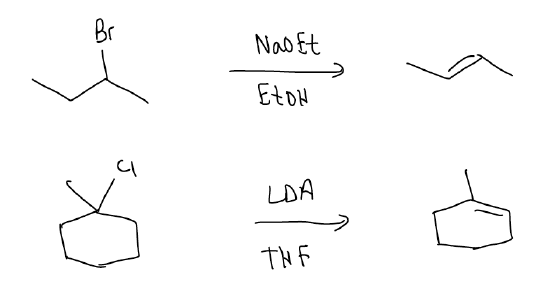
If we combine the effects of regioselectivity and stereoselectivity, we should be able to predict the major product from the following reaction:

The E₁ reaction can also occur for tertiary and secondary alkyl halides. In this case, a strong base is needed to perform the deprotonation, but all of the other rules still apply. There must be overlap between at \(σ_{C-H}\) and the atomic p orbital, Zaitsev’s rule is followed, and the reaction is stereoselective. The rate depends, again, on the leaving group ability and structure of the alkyl halide (hence, first order): rate = k [alkyl halide].