7.3: Absolute Configuration

Let’s recall the electrophilic addition reaction that we learned about before. In this reaction, protonation gives a carbocationic intermediate that has an empty atomic p orbital. Since the atomic p orbital lies above and below the plane of the trigonal planar carbon, there is equal chance of attack of the nucleophile from the top or bottom face. If we look at the products that result from these two scenarios, we should notice that attack on one face gives one enantiomer, while attack on the other gives the mirror image. We say that the carbocation (which is achiral) has two enantiotopic faces, meaning if it is attacked, it will give one enantiomer or the other. Because there is equal chance of attack from the top and bottom faces, the energy barrier to form each enantiomer is identical, so a racemic mixture of enantiomers results.

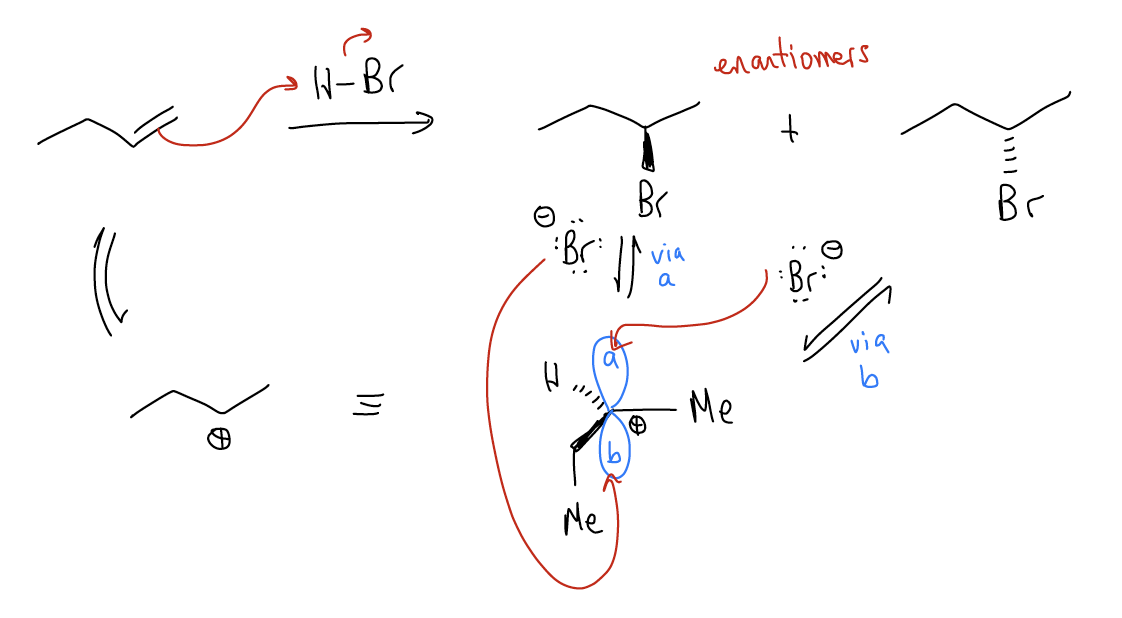
So, how do we communicate if we have one enantiomer or the other? Just as in the naming of alkenes, we use the Cahn-Ingold-Prelog convention, which is based on the atomic number of the attached groups.

1. Rank the groups attached to a stereocenter based on atomic number (1 = highest priority, 4 = lowest priority)
2. Rotate the molecule (USE A MODEL KIT!) so that the lowest priority group faces away from you.
3. Draw a circle from the highest priority group to the next highest priority to the next highest priority (ignoring the lowest priority group).
4. If your rotation is clockwise, we say that it is an R stereocenter (a little mnemonic – a steering wheel rotates clockwise to steer right = R); if the rotation is counterclockwise, we that it is an S stereocenter.

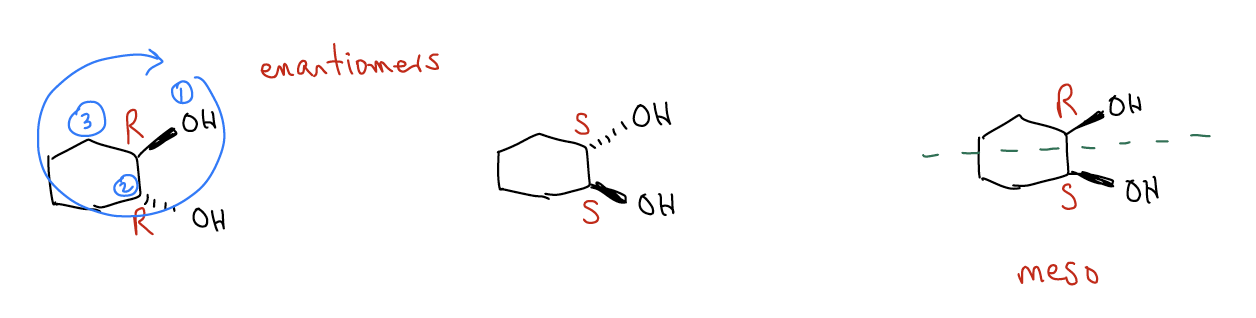
The R and S designations are what we call the absolute configuration. This is different from relative configuration, which are things like cis and trans. Both of the following compounds have a trans relative configuration, but they have the exact opposite absolute configurations. These are enantiomers. Reflection of a chiral center through a plane of symmetry will convert from one absolute configuration to the other (as is the case with the meso compound on the right).

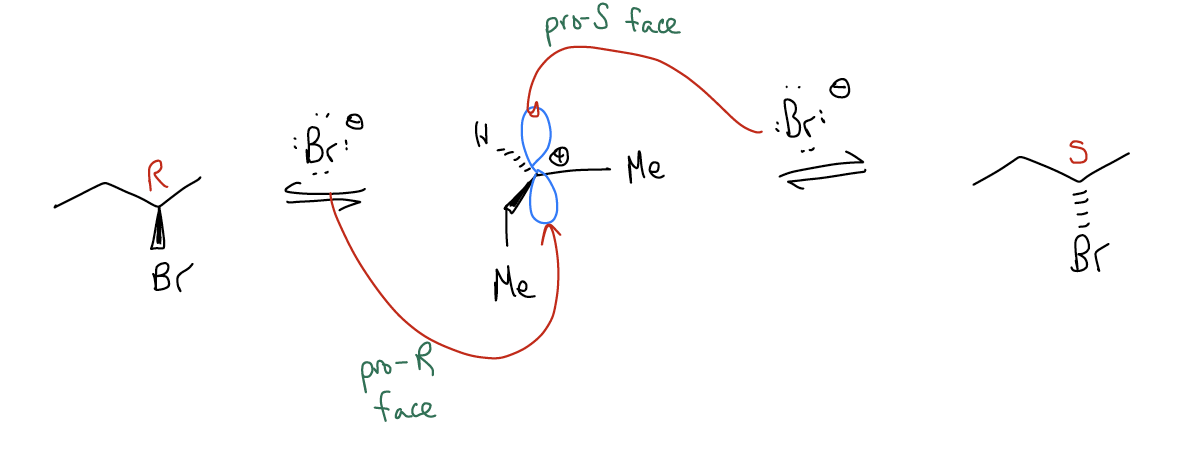
If we go back to our electrophilic addition reaction, remember that the second step is the stereochemistry-determining step. Attack of the atomic p orbital from one face will give you the R enantiomer, while attack of the other face will give you the S enantiomer. We say that these two faces of the atomic p orbital are pro-R and pro-S, respectively.

Biomedical Spotlight

Absolute configuration (R/S) assigns the stereochemical arrangement of groups around individual stereocenters according to the rules of the Cahn-Ingold-Prelog convention. In biochemistry, there is an additional nomenclature system that you may come across that is a bit antiquated. The Fischer-Rosanoff convention assigns entire molecules (not individual stereocenters) as D/L (dextrorotatory/levorotatory) based on the relative orientation of the substituent groups when compared to the enantiomers of the biomolecule glyceraldehyde. Compounds that arrange the substituent groups in the same way as (+)-glyceraldehyde are given the designation D, while compounds that arrange the substituent groups in the same way as (–)-glyceraldehyde are given the designation L.

Why is all of this important? Because you will often see D/L designations in the literature to describe amino acids, sugars, and other small molecules. For example, there is both D-(+)-glucose and L-(–)-glucose. But be careful, the D/L designations have no correlation to optical activity (+/–), and correspond to the molecule as a whole (saying nothing about individual stereogenic centers). For example, the D- and L-forms of ribose are D-(–)-ribose and L-(+)-ribose, respectively.

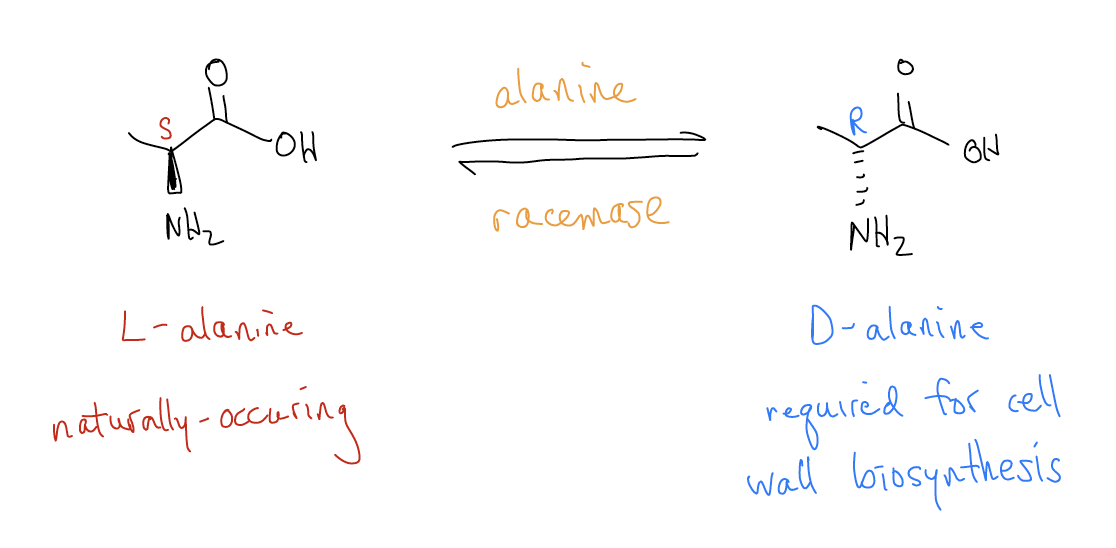
One important example of D/L-designations and its relation to absolute configuration comes from microbiology. Cells in the animal kingdom have phospholipid bilayer-derived membranes, but microorganisms like bacteria have an additional shell of protection known as cell walls. Cell walls are composed of densely-packed carbohydrate-peptide conjugates. This peptidoglycan cell wall is largely made up of the L-amino acids, with two exceptions. Bacteria require D-alanine and D-glutamate for cell wall biosynthesis. This is striking since most of the living world is homochiral, incorporating only small molecules with the L-configuration that exist naturally. As such, bacteria have evolved a mechanism to convert L-alanine into D-alanine using an enzyme, alanine racemase. This enzyme binds the naturally-occuring L-alanine (with corresponding S absolute configuration) and converts it into D-alanine (inverting the stereocenter into its R absolute configuration).

Adapted from Hallelujah Moments, by Eugene Cordes, 2014

One might think that exploiting this pathway as a mechanism for creating new antibiotics would be viable, since creating an inhibitor of alanine racemase would have no effect on human health. Merck devised an antibiotic research program to test this hypothesis. However, creating a small molecule that could inhibit alanine racemase and be safe was a problem that could not be overcome, and the project was abandoned.