10.1: Fluorescence and Phosphorescence
- Page ID
- 222275
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Fluorescence and phosphorescence are types of molecular luminescence methods. A molecule of analyte absorbs a photon and excites a species. The emission spectrum can provide qualitative and quantitative analysis. The term fluorescence and phosphorescence are usually referred as photoluminescence because both are alike in excitation brought by absorption of a photon. Fluorescence differs from phosphorescence in that the electronic energy transition that is responsible for fluorescence does not change in electron spin, which results in short-live electrons (<10-5 s) in the excited state of fluorescence. In phosphorescence, there is a change in electron spin, which results in a longer lifetime of the excited state (second to minutes). Fluorescence and phosphorescence occurs at longer wavelength than the excitation radiation.
Introduction
Fluorescence can occur in gaseous, liquid, and solid chemical systems. The simple kind of fluorescence is by dilute atomic vapors. A fluorescence example would be if a 3s electron of a vaporized sodium atom is excited to the 3p state by absorption of a radiation at wavelength 589.6 and 589.0 nm. After 10-8 s, the electron returns to ground state and on its return it emits radiation of the two wavelengths in all directions. This type of fluorescence in which the absorbed radiation is remitted without a change in frequency is known as resonance fluorescence. Resonance fluorescence can also occur in molecular species. Molecular fluorescence band centers at wavelengths longer than resonance lines. The shift toward longer wavelength is referred to as the Stokes Shift.
Singlet and Triplet Excited State
Understanding the difference between fluorescence and phosphorescence requires the knowledge of electron spin and the differences between singlet and triplet states. The Pauli Exclusion principle states that two electrons in an atom cannot have the same four quantum numbers (\(n\), \(l\), \(m_l\), \(m_s\)) and only two electrons can occupy each orbital where they must have opposite spin states. These opposite spin states are called spin pairing. Because of this spin pairing, most molecules do not exhibit a magnetic field and are diamagnetic. In diamagnetic molecules, electrons are not attracted or repelled by the static electric field. Free radicals are paramagnetic because they contain unpaired electrons have magnetic moments that are attracted to the magnetic field.
Singlet state is defined when all the electron spins are paired in the molecular electronic state and the electronic energy levels do not split when the molecule is exposed into a magnetic field. A doublet state occurs when there is an unpaired electron that gives two possible orientations when exposed in a magnetic field and imparts different energy to the system. A singlet or a triplet can form when one electron is excited to a higher energy level. In an excited singlet state, the electron is promoted in the same spin orientation as it was in the ground state (paired). In a triplet excited stated, the electron that is promoted has the same spin orientation (parallel) to the other unpaired electron. The difference between the spins of ground singlet, excited singlet, and excited triplet is shown in Figure \(\PageIndex{1}\). Singlet, doublet and triplet is derived using the equation for multiplicity, 2S+1, where S is the total spin angular momentum (sum of all the electron spins). Individual spins are denoted as spin up (s = +1/2) or spin down (s = -1/2). If we were to calculated the S for the excited singlet state, the equation would be 2(+1/2 + -1/2)+1 = 2(0)+1 = 1, therefore making the center orbital in the figure a singlet state. If the spin multiplicity for the excited triplet state was calculated, we obtain 2(+1/2 + +1/2)+1 = 2(1)+1 =3, which gives a triplet state as expected.
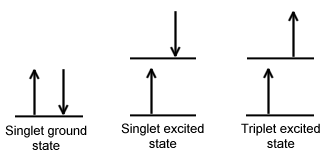
The difference between a molecule in the ground and excited state is that the electrons is diamagnetic in the ground state and paramagnetic in the triplet state.This difference in spin state makes the transition from singlet to triplet (or triplet to singlet) more improbable than the singlet-to-singlet transitions. This singlet to triplet (or reverse) transition involves a change in electronic state. For this reason, the lifetime of the triplet state is longer the singlet state by approximately 104 seconds fold difference.The radiation that induced the transition from ground to excited triplet state has a low probability of occurring, thus their absorption bands are less intense than singlet-singlet state absorption. The excited triplet state can be populated from the excited singlet state of certain molecules which results in phosphorescence. These spin multiplicities in ground and excited states can be used to explain transition in photoluminescence molecules by the Jablonski diagram.
Jablonski Diagrams
The Jablonski diagram that drawn below is a partial energy diagram that represents the energy of photoluminescent molecule in its different energy states. The lowest and darkest horizontal line represents the ground-state electronic energy of the molecule which is the singlet state labeled as \(S_o\). At room temperature, majority of the molecules in a solution are in this state.
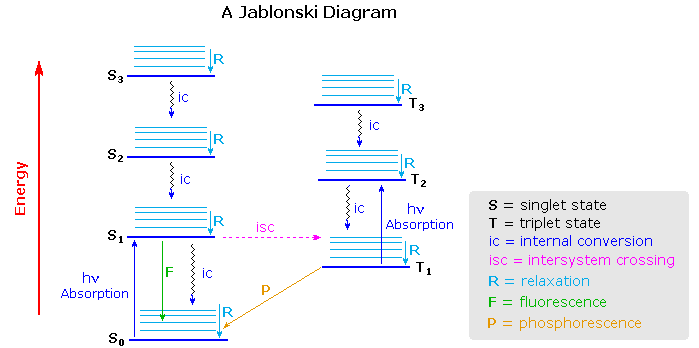
The upper lines represent the energy state of the three excited electronic states: S1and S2 represent the electronic singlet state (left) and T1 represents the first electronic triplet state (right). The upper darkest line represents the ground vibrational state of the three excited electronic state.The energy of the triplet state is lower than the energy of the corresponding singlet state.
There are numerous vibrational levels that can be associated with each electronic state as denoted by the thinner lines. Absorption transitions (blues lines in Figure \(\PageIndex{2}\)) can occur from the ground singlet electronic state (So) to various vibrational levels in the singlet excited vibrational states. It is unlikely that a transition from the ground singlet electronic state to the triplet electronic state because the electron spin is parallel to the spin in its ground state (Figure \(\PageIndex{1}\)). This transition leads to a change in multiplicity and thus has a low probability of occurring which is a forbidden transition. Molecules also go through vibration relaxation to lose any excess vibrational energy that remains when excited to the electronic states (\(S_1\) and \(S_2\)) as demonstrated in wavy lines in Figure \(\PageIndex{2}\). The knowledge of forbidden transition is used to explain and compare the peaks of absorption and emission.
Absorption and Emission Rates
The table below compares the absorption and emission rates of fluorescence and phosphorescence.The rate of photon absorption is very rapid. Fluorescence emission occurs at a slower rate.Since the triplet to singlet (or reverse) is a forbidden transition, meaning it is less likely to occur than the singlet-to-singlet transition, the rate of triplet to singlet is typically slower. Therefore, phosphorescence emission requires more time than fluorescence.
| Process | Transition | Timescale (sec) |
|---|---|---|
| Light Absorption (Excitation) | S0 → Sn | ca. 10-15 (instantaneous) |
| Internal Conversion | Sn → S1 | 10-14 to 10-11 |
| Vibrational Relaxation | Sn* → Sn | 10-12 to 10-10 |
| Intersystem Crossing | S1 → T1 | 10-11 to 10-6 |
| Fluorescence | S1 → S0 | 10-9 to 10-6 |
| Phosphorescence | T1 → S0 | 10-3 to 100 |
| Non-Radiative Decay | S1 → S0 T1 → S0 |
10-7 to 10-5 10-3 to 100 |
Deactivation Processes
A molecule that is excited can return to the ground state by several combinations of mechanical steps that will be described below and shown in Figure \(\PageIndex{2}\).The deactivation process of fluorescence and phosphorescence involve an emission of a photon radiation as shown by the straight arrow in Figure \(\PageIndex{2}\). The wiggly arrows in Figure \(\PageIndex{2}\) are deactivation processes without the use of radiation. The favored deactivation process is the route that is most rapid and spends less time in the excited state.If the rate constant for fluorescence is more favorable in the radiationless path, the fluorescence will be less intense or absent.
- Vibrational Relaxation: A molecule maybe to promoted to several vibrational levels during the electronic excitation process.Collision of molecules with the excited species and solvent leads to rapid energy transfer and a slight increase in temperature of the solvent. Vibrational relaxation is so rapid that the lifetime of a vibrational excited molecule (<10-12) is less than the lifetime of the electronically excited state. For this reason, fluorescence from a solution always involves the transition of the lowest vibrational level of the excited state. Since the space of the emission lines are so close together, the transition of the vibrational relaxation can terminate in any vibrational level of the ground state.
- Internal Conversion: Internal conversion is an intermolecular process of molecule that passes to a lower electronic state without the emission of radiation.It is a crossover of two states with the same multiplicity meaning singlet-to-singlet or triplet-to-triplet states.The internal conversion is more efficient when two electronic energy levels are close enough that two vibrational energy levels can overlap as shown in between S1 and S2. Internal conversion can also occur between S0 and S1 from a loss of energy by fluorescence from a higher excited state, but it is less probable. The mechanism of internal conversion from S1 to S0 is poorly understood. For some molecules, the vibrational levels of the ground state overlaps with the first excited electronic state, which leads to fast deactivation.These usually occur with aliphatic compounds (compound that do not contain ring structure), which would account for the compound is seldom fluorescing. Deactivation by energy transfer of these molecules occurs so rapidly that the molecule does not have time to fluoresce.
- External Conversion: Deactivation of the excited electronic state may also involve the interaction and energy transfer between the excited state and the solvent or solute in a process called external conversion. Low temperature and high viscosity leads to enhanced fluorescence because they reduce the number of collision between molecules, thus slowing down the deactivation process.
- Intersystem Crossing: Intersystem crossing is a process where there is a crossover between electronic states of different multiplicity as demonstrated in the singlet state to a triplet state (S1 to T1) on Figure \(\PageIndex{1}\). The probability of intersystem crossing is enhanced if the vibration levels of the two states overlap. Intersystem crossing is most commonly observed with molecules that contain heavy atom such as iodine or bromine. The spin and orbital interaction increase and the spin become more favorable.Paramagnetic species also enhances intersystem crossing, which consequently decreases fluorescence.
- Phosphorescence: Deactivation of the electronic excited state is also involved in phosphorescence. After the molecule transitions through intersystem crossing to the triplet state, further deactivation occurs through internal or external fluorescence or phosphorescence. A triplet-to-singlet transition is more probable than a singlet-to-singlet internal crossing. In phosphorescence, the excited state lifetime is inversely proportional to the probability that the molecule will transition back to the ground state. Since the lifetime of the molecule in the triplet state is large (10-4 to 10 second or more), transition is less probable which suggest that it will persist for some time even after irradiation has stopped. Since the external and internal conversion compete so effectively with phosphorescence, the molecule has to be observed at lower temperature in highly viscous media to protect the triplet state.
Variables that affect Fluorescence
After discussing all the possible deactivation processes, variable that affect the emissions to occur. Molecular structure and its chemical environment influence whether a substance will fluoresce and the intensities of these emissions. The quantum yield or quantum efficiency is used to measure the probability that a molecule will fluoresce or phosphoresce. For fluorescence and phosphorescence is the ratio of the number of molecules that luminescent to the total number of excited molecules. For highly fluoresce molecules, the quantum efficiency approaches to one.Molecules that do not fluoresce have quantum efficiencies that approach to zero.
Fluorescence quantum yield (\( \phi \)) for a compound is determined by the relative rate constants (k) of various deactivation processes by which the lowest excited singlet state is deactivated to the ground state. The deactivation processes including fluorescence (kf), intersystem crossing (\(k_i\)), internal conversion (kic), predissociation (kpd), dissociation (kd), and external conversion (kec) allows one to qualitatively interpret the structural and environmental factors that influence the intensity of the fluorescence. They are related by the quantum yield equation given below:
\[ \dfrac{k_f}{k_f+k_i+k_{ec}+k_{ic}+k_{pd}+k_d} \]
Using this equation as an example to explain fluorescence, a high fluorescence rate (kf) value and low values of the all the other relative rate constant terms (kf +ki+kec+kic+kpd+kd) will give a large \( \phi \), which suggest that fluorescence is enhanced. The magnitudes of kf , kd, and kpd depend on the chemical structure, while the rest of the constants ki, kec, and kic are strongly influenced by the environment.
Fluorescence rarely results from absorption of ultraviolet radiation of wavelength shorter than 250 nm because radiation at this wavelength has sufficient energy to deactivate the electron in the excited state by predissociation or dissociation. The bond of some organic molecules would rupture at 140 kcal/mol, which corresponds to 200-nm of radiation. For this reason, \(\sigma \rightarrow \sigma^{*}\) transition in fluorescence are rarely observed. Instead, emissions from the less energetic transition will occur which are either \(\pi^{*} \rightarrow \pi \) or \(\pi^{*} \rightarrow n \) transition.
Molecules that are excited electronically will return to the lowest excited state by rapid vibrational relaxation and internal conversion, which produces no radiation emission. Fluorescence arises from a transition from the lowest vibrational level of the first excited electronic state to one of the vibrational levels in the electronic ground state. In most fluorescent compounds, radiation is produced by a \(\pi^{*} \rightarrow \pi \) or \(\pi^{*} \rightarrow n \) transition depending on which requires the least energy for the transition to occur.
Fluorescence is most commonly found in compounds in which the lowest energy transition is \(\pi \rightarrow \pi^{*} \) (excited singlet state) than \(n \rightarrow \pi^{*} \) which suggest that the quantum efficiency is greater for \(\pi \rightarrow \pi^{*} \) transitions. The reason for this is that the molar absorptivity, which measures the probability that a transition will occur, of the \(\pi \rightarrow \pi^{*} \) transition is 100 to 1000 fold greater than \(n \rightarrow \pi^{*} \) process. The lifetime of \(\pi \rightarrow \pi^{*} \) (10-7 to 10-9 s) is shorter than the lifetime of \(n \rightarrow \pi^{*} \) (10-5 to 10-7).
Phosphorescent quantum efficiency is the opposite of fluorescence in that it occurs in the \(n \rightarrow \pi^{*} \) excited state which tends to be short lived and less suceptable to deactivation than the \(\pi \rightarrow \pi^{*} \) triplet state. Intersystem crossing is also more probable for \(\pi \rightarrow \pi^{*} \) excited state than for the \(n \rightarrow \pi^{*} \)state because the energy difference between the singlet and triplet state is large and spin-orbit coupling is less likely to occur.
Fluorescence and Structure
The most intense fluorescence is found in compounds containing aromatic group with low-energy \(\pi \rightarrow \pi^{*} \) transitions. A few aliphatic, alicyclic carbonyl, and highly conjugated double-bond structures also exhibit fluorescence as well. Most unsubstituted aromatic hydrocarbons fluoresce in solution too. The quantum efficiency increases as the number of rings and the degree of condensation increases. Simple heterocycles such as the structures listed below do not exhibit fluorescence.
.png?revision=1)

Pyridine Pyrrole Furan Thiophene
With nitrogen heterocyclics, the lowest energy transitions is involved in \(n \rightarrow \pi^{*} \) system that rapidly converts to the triplet state and prevents fluorescence. Although simple heterocyclics do not fluoresce, fused-ring structures do. For instance, a fusion of a benzene ring to a hetercyclic structure results in an increase in molar absorptivity of the absorption band. The lifetime of the excited state in fused structure and fluorescence is observed. Examples of fluorescent compounds is shown below.

quinoline
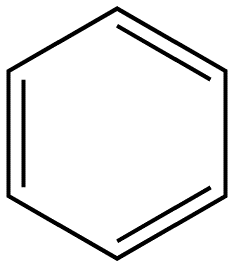
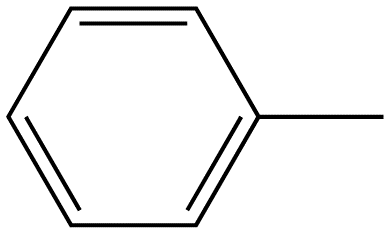
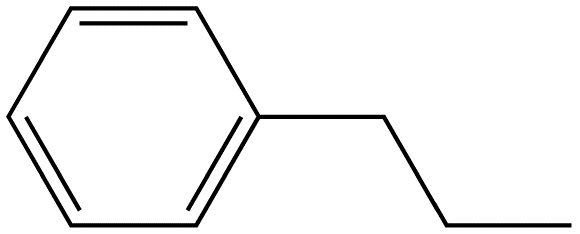
Benzene ring substitution causes a shift in the absorption maxima of the wavelength and changes in fluorescence emission. The table below is used to demonstrate and visually show that as benzene is substituted with increasing methyl addition, the relative intensity of fluorescence increases.
|
Compound |
Structure |
Wavelength of Fluorescence (nm) |
Relative intensity of Fluorescence |
|---|---|---|---|
|
Benzene |
|
270-310 |
10 |
|
Toluene |
|
270-320 |
17 |
|
Propyl Benzene |
|
270-320 |
17 |
The relative intensity of fluorescence increases as oxygenated species increases in substitution. The values for such increase is demonstrated in the table below.
|
Compound |
Structure |
Wavelength of Fluorescence (nm) |
Relative intensity of Fluorescence |
|---|---|---|---|
|
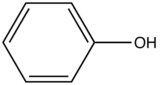
Phenol |
|
285-365 |
18 |
|
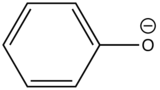
Phenolate ion |
|
310-400 |
10 |
|
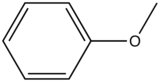
Anisole |
|
285-345 |
20 |
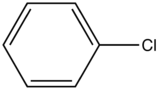
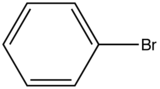
Influence of a halogen substitution decreases fluorescence as the molar mass of the halogen increases. This is an example of the “heavy atom effect” which suggest that the probability of intersystem crossing increases as the size of the molecule increases. As demonstrated in the table below, as the molar mass of the substituted compound increases, the relative intensity of the fluorescence decreases.
|
Compound |
Structure |
Wavelength of Fluorescence (nm) |
Relative intensity of Fluorescence |
|---|---|---|---|
|
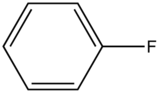
Fluorobenzene |
|
270-320 |
10 |
|
Chlorobenzene |
|
275-345 |
7 |
|
Bromobenzene |
|
290-380 |
5 |
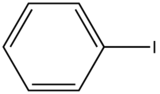
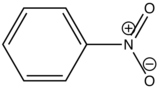
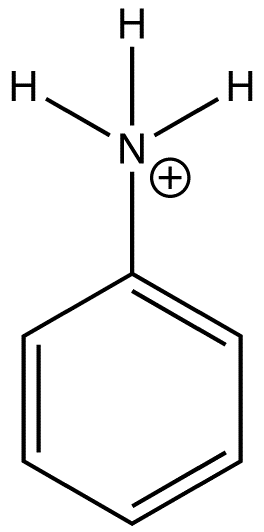
In heavy atom substitution such as nitro derivatives or heavy halogen substitution such as iodobenzene, the compounds are subject to predissociation. These compounds have bonds that easily rupture that can then absorb excitation energy and go through internal conversion. Therefore, the relative intensity of fluorescence and fluorescent wavelength is not observed and this is demonstrated in the table below.
|
Compound |
Structure |
Wavelength of Fluorescence (nm) |
Relative intensity of Fluorescence |
|---|---|---|---|
|
Iodobenzene |
|
None |
0 |
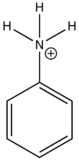
|
Anilinium ion |
|
None |
0 |
|
Nitrobenzene |
|
None |
0 |
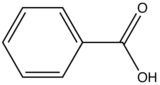
Carboxylic acid or carbonyl group on aromatic ring generally inhibits fluorescence since the energy of the \(n \rightarrow \pi^*\) transition is less than \(\pi \rightarrow \pi^*\) transition. Therefore, the fluorescence yield from \(n \rightarrow \pi^*\) transition is low.
|
Compound |
Structure |
Wavelength of Fluorescence (nm) |
Relative intensity of Fluorescence |
|---|---|---|---|
|
Benzoic Acid |
|
310-390 |
3 |
Effect of Structural Rigidity on Fluorescence
Fluorescence is particularly favored in molecules with rigid structures. The table below compares the quantum efficiencies of fluorine and biphenyl which are both similar in structure that there is a bond between the two benzene group. The difference is that fluorene is more rigid from the addition methylene bridging group. By looking at the table below, rigid fluorene has a higher quantum efficiency than unrigid biphenyl which indicates that fluorescence is favored in rigid molecules.
|
Compound |
Structure |
Quantum Efficiency |
|---|---|---|
|
Fluorene |
|
1.0 |
|
Biphenyl |
|
0.2 |
This concept of rigidity was used to explain the increase in fluorescence of organic chelating agent when the compound is complexed with a metal ion. The fluorescence intensity of 8-hydroxyquinoline is much less than its zinc complex.
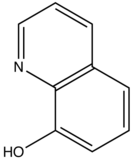 vs
vs 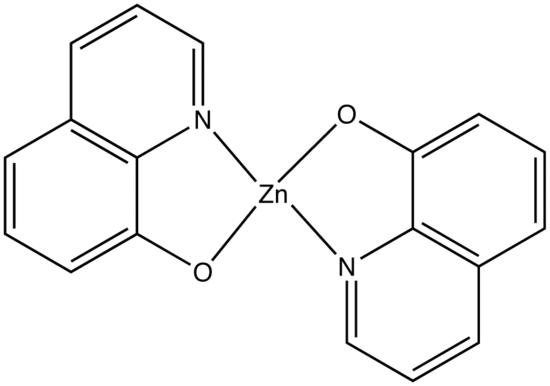
8-hydroxyquinoline 8-hydroxyquinoline with Zinc complexed
The explanation for lower quantum efficiency or lack of rigidity in caused by the enhanced internal conversion rate (kic) which increases the probability that there will be radiationless deactivation. Nonrigid molecules can also undergo low-frequency vibration which accounts for small energy loss.
Temperature and Solvent Effects
Quantum efficiency of Fluorescence decreases with increasing temperature. As the temperature increases, the frequency of the collision increases which increases the probability of deactivation by external conversion. Solvents with lower viscosity have higher possibility of deactivation by external conversion. Fluorescence of a molecule decreases when its solvent contains heavy atoms such as carbon tetrabromide and ethyl iodide, or when heavy atoms are substituted into the fluorescing compound. Orbital spin interaction result from an increase in the rate of triplet formation, which decreases the possibility of fluorescence. Heavy atoms are usually incorporated into solvent to enhance phosphorescence.
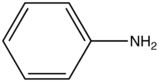
Effect of pH on Fluorescence
The fluorescence of aromatic compound with basic or acid substituent rings are usually pH dependent. The wavelength and emission intensity is different for protonated and unprotonated forms of the compound as illustrated in the table below:
|
Compound |
Structure |
Wavelength of Fluorescence (nm) |
Relative intensity of Fluorescence |
|---|---|---|---|
|
aniline |
310-405 |
20 |
|
|
Anilinium ion |
None |
0 |
The emission changes of this compound arises from different number of resonance structures associated with the acidic and basic forms of the molecule.The additional resonance forms provides a more stable first excited state, thus leading to fluorescence in the ultraviolet region.The resonance structures of basic aniline and acidic anilinium ion is shown below:
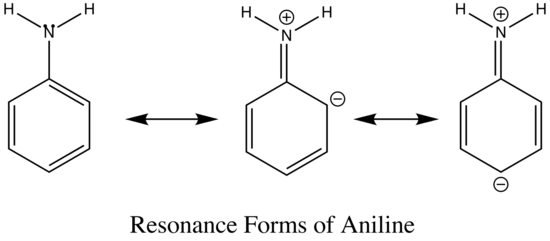
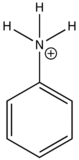
basic Aniline Fluorescence of certain compounds have been used a detection of end points in acid-base titrations.An example of this type of fluorescence seen in compound as a function of pH is the phenolic form of 1-naphthol-4-sulfonic acid.This compound is not detectable with the eye because it occurs in the ultraviolet region, but with an addition of a base, it becomes converted to a phenolate ion, the emission band shifts to the visible wavelength where it can be visually seen. Acid dissociation constant for excited molecules differs for the same species in the ground state.These changes in acid or base dissociation constant differ in four or five orders of magnitude.
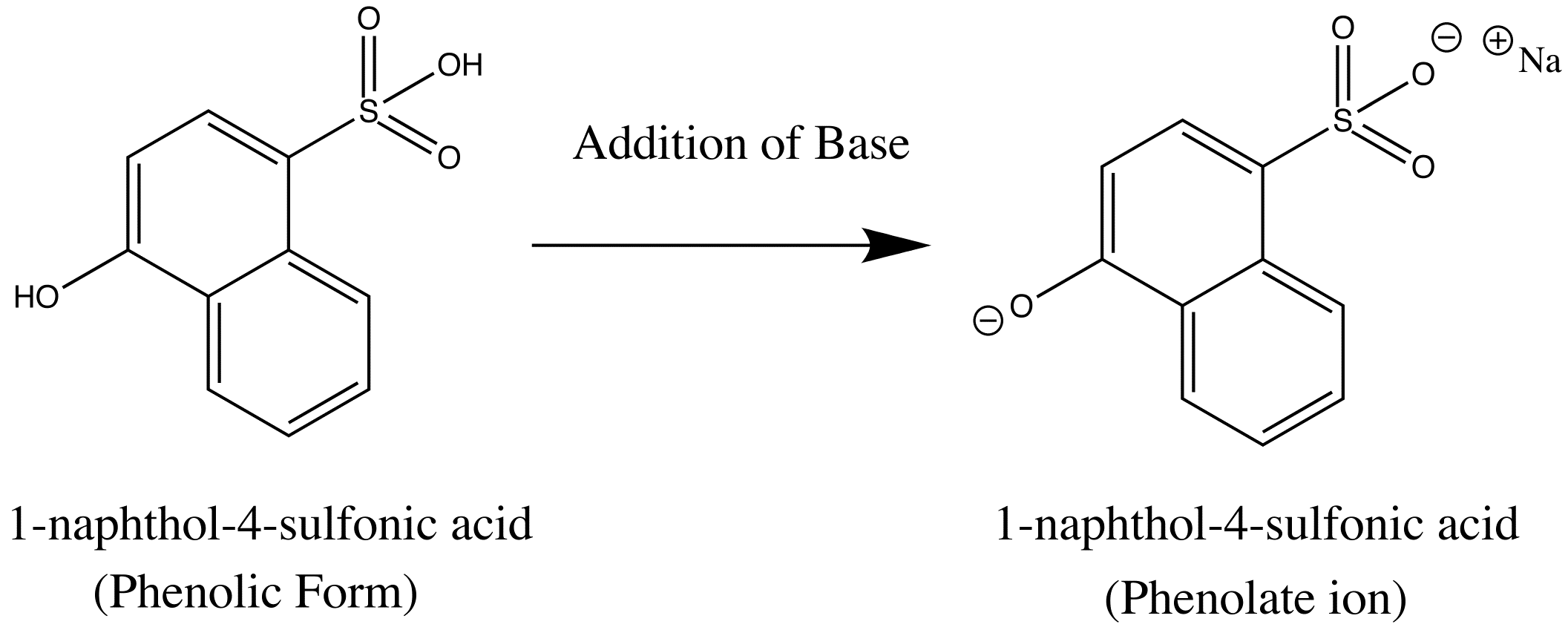
Dissolved oxygen reduces the intensity of fluorescence in solution, which results from a photochemically induced oxidation of fluorescing species.Quenching takes place from the paramagnetic properties of molecular oxygen that promotes intersystem crossing and conversion of excited molecules to triplet state.Paramagnetic properties tend to quench fluorescence.
Effects of Concentration on Fluorescence Intensity
The power of fluorescence emission \(F\) is proportional to the radiant power is proportional to the radiant power of the excitation beam that is absorbed by the system. The equation below best describes this relationship.
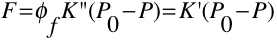 (1)
(1)
Since \(\phi_f K”\) is constant in the system, it is represented at K’. The table below defines the variables in this equation.
|
Variable |
Definition |
|---|---|
|
F |
Power of fluorescence emission |
|
P0 |
Power of incident beam on solution |
|
P |
Power after transversing length b in medium |
|
K” |
Constant dependent on geometry and other factors |
|
|
Quantum efficiency |
Fluorescence emission (\(F\)) can be related to concentration (\(c\)) using Beer’s Law stating:
\[ F = \epsilon b c \label{2}\]
where \( \epsilon \) is the molar absorptivity of the molecule that is fluorescing. Rewriting Equation 2 gives:
\[ P =P_0 10^{-\epsilon b c} \label{3}\]
Substituting Equation \(\ref{3}\) into Equation \(\ref{2}\) and factoring out \(P_0\) gives us this equation:
\[F=K^{\prime} P_{0}\left(1-10^{-\varepsilon b c}\right)\]
The MacLaurin series could be used to solved the exponential term.
\[F=K^{\prime} P_{0}\left[2.303 \varepsilon b c-\frac{(2.303 \varepsilon b c)^{2}}{2 !}+\frac{(2.303 \varepsilon b c)^{3}}{3 !}+\frac{(2.303 \varepsilon b c)^{4}}{4 !}+\ldots \frac{(2.303 \varepsilon b c)^{n}}{n !}\right]_{1}\label{5}\]
Given that \((2.303 \epsilon b c = \text{Absorbance} <0.05\), all the subsequent terms after the first can be dropped since the maximum error is 0.13%. Using only the first term, Equation \(\ref{5}\) can be rewritten as:
\[F=K^{\prime} P_{0} 2.303 \varepsilon b c\label{6}\]
Equation \(\ref{6}\) can be expanded to the equation below and simplified to compare the fluorescence emission F with concentration. If the equation below were to be plotted with F versus c, a linear relation would be observed.
\[F=\phi_{f} K^{\prime \prime} P_{0} 2.303 \varepsilon b c\]
If \(c\) becomes so great that the absorbance > 0.05, the higher terms in Equation \(\ref{5}\) start to become more important and the linearity is lost. F then lies below the extrapolation of the straight-line plot. This excessive absorption is the primary absorption. Another cause of this negative downfall of linearity is the secondary absorption when the wavelength of emission overlaps the absorption band. This occurs when the emission transverse the solution and gets reabsorbed by other molecules by analyte or other species in the solution, which leads to a decrease in fluorescence.
Quenching Methods
Dynamic Quenching is a nonradiative energy transfer between the excited and the quenching agent species (Q).The requirements for a successful dynamic quenching are that the two collision species the concentration must be high so that there is a higher possibility of collision between the two species.Temperature and quenching agent viscosity play a role on the rate of dynamic quenching.Dynamic quenching reduces fluorescence quantum yield and the fluorescence lifetime.
Dissolved oxygen in a solution increases the intensity of the fluorescence by photochemically inducing oxidation of the fluorescing species.Quenching results from the paramagnetic properties of molecular oxygen that promotes intersystem crossing and converts the excited molecules to triplet state.Paramagnetic species and dissolved oxygen tend to quench fluorescence and quench the triplet state.
Static quenching occurs when the quencher and ground state fluorophore forms a dark complex.Fluorescence is usually observed from unbound fluorophore.Static quenching can be differentiated from dynamic quenching in that the lifetime is not affected in static quenching.In long range (Förster) quenching, energy transfer occurs without collision between molecules, but dipole-dipole coupling occurs between excited fluorophore and quencher.
Emission and Excitation Spectra
One of the ways to visually distinguish the difference between each photoluminescence is to compare the relative intensities of emission/excitation at each wavelength. An example of the three types of photoluminescence (absorption, fluorescence and phosphorescence) is shown for phenanthrene in the spectrum below.In the spectrum, the luminescent intensity is measure in a wavelength is fixed while the excitation wavelength is varied. The spectrum in red represents the excitation spectrum, which is identical to the absorption spectrum because in order for fluorescence emission to occur, radiation needs to be absorbed to create an excited state.The spectrum in blue represent fluorescence and green spectrum represents the phosphorescence.
.png?revision=1&size=bestfit&width=580&height=392)
As a real example illustrating the "mirror" relationship between the absorbance and emission spectra is shown in Figure 4. Figure 4 depicts a small portion of the absorbance spectrum for fluorescein in blue as well as the and fluorescence spectra in red. Fluorescein is a common dye used in analytical chemistry as well as ophthalmology.
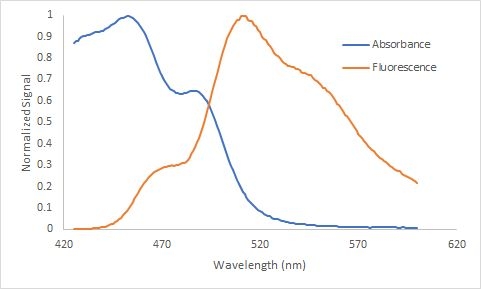
Figure 4. The absorbance and fluorescence spectrum for fluorescein illustrating the "mirroring" between the two spectra because of the similarity in energy level spacing within the ground state and lowest excited state. The two spectra also illustrate the Stokes shift, the emission of light at a longer wavelength than the excitation wavelength, \({\lambda}\)max for emission ~ 520 nm and \({\lambda}\)max for excitation ~ 450 nm. Both spectra are normalized and the concentration for the absorbance spectrum is 3 x 10-6 M and the the fluorescence spectrum 1 x 10-7 M.
Fluorescence and Phosphorescence occur at wavelengths that are longer than their absorption wavelengths.Phosphorescence bands are found at a longer wavelength than fluorescence band because the excited triplet state is lower in energy than the singlet state.The difference in wavelength could also be used to measure the energy difference between the singlet and triplet state of the molecule. The wavelength (\(\lambda\)) of a molecule is inversely related to the energy (\(E\)) by the equation below:
\[E= \dfrac{hc}{\lambda}\]
As the wavelength increases, the energy of the molecule decrease and vice versa.
References
- D. A. Skoog, et al. "Principles of Instrumental Analysis" 6th Edition, Thomson Brooks/Cole. 2007
- D. C. Harris and M.D. Bertolucci "Symmetry and Spectroscopy, An Introduction to Vibrational and Electronic Spectroscopy" Dover Publications, Inc., New York. 1989.
Problems
- Draw and label the Jablonski Diagram.
- How do spin states differ in ground singlet state versus excite singlet state and triplet excited state?
- Describe the rates of deactivation process.
- What is quantum yield and how is it used to compare the fluorescence of different types of molecule?
- What roles do solvent play in fluorescence?
Contributors
- Diana Wong (UCD)


.png?revision=1)

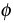 f
f