6.2.2: The Law of Reflection

Last updated
Save as PDF

Page ID: 220528

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Learning Objectives

By the end of this section, you will be able to:

Explain the reflection of light from polished and rough surfaces
Describe the reflection of the interface between two transparent media

Whenever we look into a mirror, or squint at sunlight glinting from a lake, we are seeing a reflection. When you look at a piece of white paper, you are seeing light scattered from it. Large telescopes use reflection to form an image of stars and other astronomical objects.

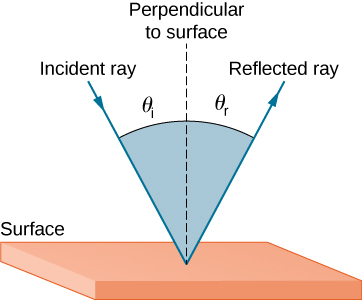
The law of reflection states that the angle of reflection equals the angle of incidence:

\[θ_r=θ_i \label{law of reflection}\]

The law of reflection is illustrated in Figure \(\PageIndex{1}\), which also shows how the angle of incidence and angle of reflection are measured relative to the perpendicular to the surface at the point where the light ray strikes.

A light ray is incident on a smooth surface and is making an angle theta i relative to a line drawn perpendicular to the surface at the point where the incident ray strikes it. The reflected light ray makes an angle theta r with the same perpendicular drawn to the surface. Both incident and reflected ray are on the same side of the surface but opposite sides of the perpendicular line. — Figure \(\PageIndex{1}\): The law of reflection states that the angle of reflection equals the angle of incidence θ_r= θ_i. The angles are measured relative to the perpendicular to the surface at the point where the ray strikes the surface.

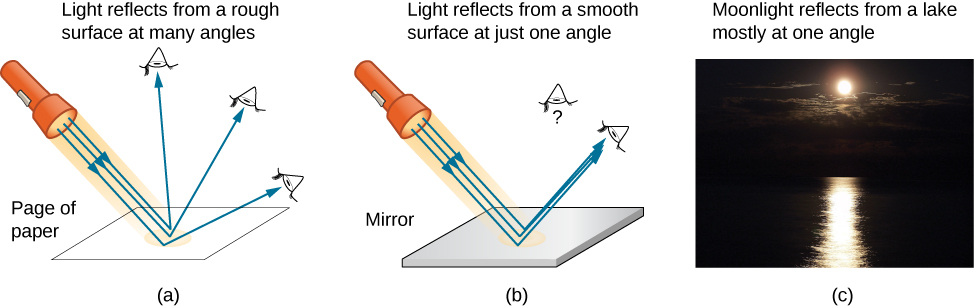
We expect to see reflections from smooth surfaces, but Figure \(\PageIndex{2}\) illustrates how a rough surface reflects light. Since the light strikes different parts of the surface at different angles, it is reflected in many different directions, or diffused. Diffused light is what allows us to see a sheet of paper from any angle, as shown in Figure \(\PageIndex{1a}\).

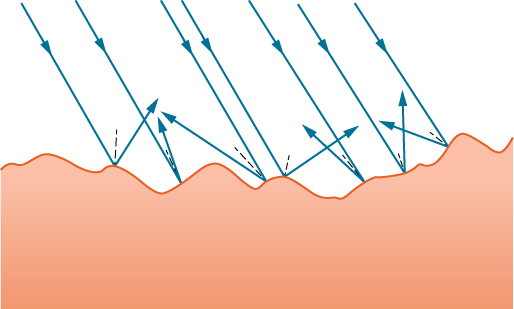
The figure shown parallel light rays falling on a rough surface. The rays hit the surface at different angles to the perpendicular lines to the surface at the points of incidence, and the reflected rays get scattered in different directions. — Figure \(\PageIndex{2}\): Light is diffused when it reflects from a rough surface. Here, many parallel rays are incident, but they are reflected at many different angles, because the surface is rough.

People, clothing, leaves, and walls all have rough surfaces and can be seen from all sides. A mirror, on the other hand, has a smooth surface (compared with the wavelength of light) and reflects light at specific angles, as illustrated in Figure \(\PageIndex{3b}\). When the Moon reflects from a lake, as shown in Figure \(\PageIndex{1c}\), a combination of these effects takes place.

Figure a shows the rays of light from a flashlight falling on a page of paper. The light gets reflected at many angles as the surface is rough. Reflected light reaches eyes placed at many location. Figure b shows the rays of light from a flashlight falling on mirror. All of the light gets reflected at the same angle since the surface is smooth. Reflected light only reaches an eye placed so that the reflected beam hits it. An observer not at the angle of the reflected light does not see it. Figure c shows a photograph of moonlight falling on a lake. The lake’s shiny surface reflects it. A bright , slightly rippled strip of moonlight is seen reflecting from the lake on a dark background. — Figure \(\PageIndex{3}\): (a) When a sheet of paper is illuminated with many parallel incident rays, it can be seen at many different angles, because its surface is rough and diffuses the light. (b) A mirror illuminated by many parallel rays reflects them in only one direction, because its surface is very smooth. Only the observer at a particular angle sees the reflected light. (c) Moonlight is spread out when it is reflected by the lake, because the surface is shiny but uneven. (credit c: modification of work by Diego Torres Silvestre)

Reflection from the interface between two transmissive materials

Figure \(\PageIndex{4}\):illustrates what happens when electromagnetic radiation crosses a smooth interface into a dielectric medium that has a higher refractive index (\(\eta_{t}\) > \(\eta_{i}\)). We see two phenomena: reflection and refraction (a specific type of transmission). The angle of reflection, θ_r, equals the angle of incidence, θⁱ, where each is defined with respect to the surface normal. The angle of refraction, θ_t, (t for transmitted) is described by Snell’s law (of Refraction) which is described in the next section.

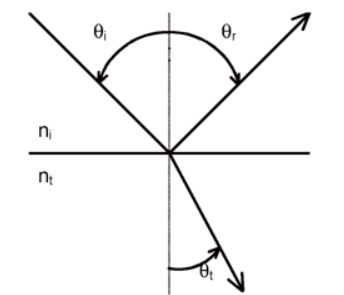
light at interface.jpg

Figure \(\PageIndex{4}\): Reflection and refraction at the interface between two transmissive materials of differing refractive indices.

The radiant power of the reflected and refracted light depend on several factors. The Fresnel equations describe the dependence of the reflected light on the angle of incidence, the refractive indices of the two media and, in some cases, the polarization of the incident beam. In the case of normal incidence, the fraction of light reflected reflectance (ρ=I_r/I₀) is

\(\rho=\left[\frac{n_{i}-n_{i}}{n_{i}+n_{i}}\right]^{2}\)

where I_r is the intensity of light reflected and I₀ is the incident intensity. The reflectance is thus related to the difference in refractive indices between the two media. For glass and air, which have refractive indices of 1.50 and 1.00, respectively, the fraction of reflected light is 0.04. For water and diamond, which has a refractive index of 2.4, the fraction of light reflected is 0.08. It is therefore easier to see diamonds in water than it is to see glass in air.

It should be noted that reflection occurs upon each pass through an interface. Consequently for light passing through a cuvette reflection will occur at 4 interfaces and the fraction of light lost due to reflection will (ρ)⁴.

An of interesting tangent that is important for the ATR accessory with our FTIR

Snell's law, \(\eta_{i} \sin \theta_{i}=\eta_{t} \sin \theta_{t}\), predicts the phenomenon of total internal reflection, depicted in Figure \(\PageIndex{5}\). Whenever light is traveling from a more optically dense medium to a less optically dense medium \(\eta_{i}\) > \(\eta_{t}\), θ_t can appear to exceed 90. In reality, most of the incident beam is totally internally reflected. At incident angles above a critical angle specified by Eqn. 4.1, the transmitted beam becomes vanishingly small and propagates parallel to the interface. This small electric field extends beyond the boundary of the interface into the lower refractive index medium for a distance approximately equal to the wavelength of light. This electric field beyond the interface is called the evanescent field, and it can be used to excite molecules on the other side (\(\eta_{t}\)) of the interface, provided they are within a distance on the order of the wavelength of light. The evanescent field strength is dependent upon the polarization (the orientation of the electric field), the angle of the incident beam and the refractive indices of the two media. The technique of “attenuated total internal reflectance”, or ATR, is commonly used in infrared spectroscopy to make measurements of films or solids by launching an IR evanescent wave into a thin layer of the material of interest adsorbed or clamped to a crystal in which an IR beam undergoes multiple internal reflections.

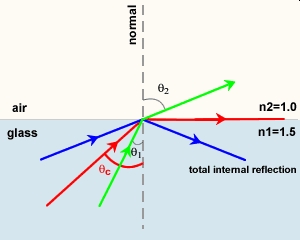
Figure \(\PageIndex{5}\): Total internal reflection for light traveling from glass to air.

Contributors and Attributions

Template:ContribOpenStaxUni