Chapter 15.5: Heats of Formation
- Page ID
- 42028
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
 |
Prince George's Community College |
 |
| Unit I: Atoms Unit II: Molecules Unit III: States of Matter Unit IV: Reactions Unit V: Kinetics & Equilibrium Unit VI: Thermo & Electrochemistry Unit VII: Nuclear Chemistry |
||
Learning Objectives
- To understand Enthalpies of Formation and be able to use them to calculated Enthalpies of Reaction
Enthalpies of Formation
Chapter 11 and Chapter 12 presented a wide variety of chemical reactions, and you learned how to write balanced chemical equations that include all the reactants and the products except heat. One way to report the heat absorbed or released would be to compile a massive set of reference tables that list the enthalpy changes for all possible chemical reactions, which would require an incredible amount of effort. Fortunately, Hess’s law allows us to calculate the enthalpy change for virtually any conceivable chemical reaction using a relatively small set of tabulated data starting from the elemental forms of each atom at 25 oC and 1 atm pressure.
-
Enthalpy of formation (ΔHf)The enthalpy change for the formation of 1 mol of a compound from its component elements.: The enthalpy change for the formation of 1 mol of a compound from its component elements, such as the formation of carbon dioxide from carbon and oxygen. The corresponding relationship is
\( elements \rightarrow compound \;\;\;\;\ \Delta H_{rxn} = \Delta H_{f} \tag{15.5.1} \)
For example,
\( C\left (s \right ) + O_{2}\left (g \right ) \rightarrow CO_{2}\left (g \right ) \; \; \; \; \Delta H_{rxn} = \Delta H_{f}\left [CO_{2}\left ( g \right ) \right ] \)The sign convention for ΔHf is the same as for any enthalpy change: ΔHf < 0 if heat is released when elements combine to form a compound and ΔHf > 0 if heat is absorbed.
Note the Pattern
The sign convention is the same for all enthalpy changes: negative if heat is released by the system and positive if heat is absorbed by the system.
Standard Enthalpies of Formation
The magnitude of ΔH for a reaction depends on the physical states of the reactants and the products (gas, liquid, solid, or solution), the pressure of any gases present, and the temperature at which the reaction is carried out. To avoid confusion caused by differences in reaction conditions and ensure uniformity of data, the scientific community has selected a specific set of conditions under which enthalpy changes are measured. These standard conditions serve as a reference point for measuring differences in enthalpy, much as sea level is the reference point for measuring the height of a mountain or for reporting the altitude of an airplane.
The standard conditionsThe conditions under which most thermochemical data are tabulated: 1 atm for all gases and a concentration of 1.0 M for all species in solution. for which most thermochemical data are tabulated are a pressure of 1 atmosphere (atm) for all gases and a concentration of 1 M for all species in solution (1 mol/L). In addition, each pure substance must be in its standard stateThe most stable form of a pure substance at a pressure of 1 atm at a specified temperature.. This is usually its most stable form at a pressure of 1 atm at a specified temperature. We assume a temperature of 25°C (298 K) for all enthalpy changes given in this text, unless otherwise indicated. Enthalpies of formation measured under these conditions are called standard enthalpies of formation (ΔHof)The enthalpy change for the formation of 1 mol of a compound from its component elements when the component elements are each in their standard states. The standard enthalpy of formation of any element in its most stable form is zero by definition. (which is pronounced “delta H eff naught”). The standard enthalpy of formation of any element in its standard state is zero by definition. For example, although oxygen can exist as ozone (O3), atomic oxygen (O), and molecular oxygen (O2), O2 is the most stable form at 1 atm pressure and 25°C. Similarly, hydrogen is H2(g), not atomic hydrogen (H). Graphite and diamond are both forms of elemental carbon, but because graphite is more stable at 1 atm pressure and 25°C, the standard state of carbon is graphite (Figure 15.5.1). Therefore, O2(g), H2(g), and graphite have ΔHof values of zero.

Figure 15.5.1 Elemental Carbon Although graphite and diamond are both forms of elemental carbon, graphite is more stable at 1 atm pressure and 25°C than diamond is. Given enough time, diamond will revert to graphite under these conditions. Hence graphite is the standard state of carbon.
The standard enthalpy of formation of glucose from the elements at 25°C is the enthalpy change for the following reaction:
\( 6C\left (s, graphite \right ) + 6H_{2}\left (g \right ) + 3O_{2}\left (g \right ) \rightarrow C_{6}H_{12}O_{6}\left (s \right )\; \; \; \Delta H_{f}^{o} = - 1273.3 \; kJ \tag{15.5.2} \)
It is not possible to measure the value of ΔHof for glucose, −1273.3 kJ/mol, by simply mixing appropriate amounts of graphite, O2, and H2 and measuring the heat evolved as glucose is formed; the reaction shown in Equation 15.5.2 does not occur at a measurable rate under any known conditions. Glucose is not unique; most compounds cannot be prepared by the chemical equations that define their standard enthalpies of formation. Instead, values of are obtained using Hess’s law and standard enthalpy changes that have been measured for other reactions, such as combustion reactions. Values of ΔHof for an extensive list of compounds are given in the Reference Tables. Note that ΔHof values are always reported in kilojoules per mole of the substance of interest. Also notice in the Reference Tables that the standard enthalpy of formation of O2(g) is zero because it is the most stable form of oxygen in its standard state.
Example 15.5.1
For the formation of each compound, write a balanced chemical equation corresponding to the standard enthalpy of formation of each compound.
- HCl(g)
- MgCO3(s)
- CH3(CH2)14CO2H(s) (palmitic acid)
Given: compound
Asked for: balanced chemical equation for its formation from elements in standard states
Strategy:
Use the Reference Tables to identify the standard state for each element. Write a chemical equation that describes the formation of the compound from the elements in their standard states and then balance it so that 1 mol of product is made.
Solution:
To calculate the standard enthalpy of formation of a compound, we must start with the elements in their standard states. The standard state of an element can be identified in the Reference Tables by a ΔHof value of 0 kJ/mol.
-
Hydrogen chloride contains one atom of hydrogen and one atom of chlorine. Because the standard states of elemental hydrogen and elemental chlorine are H2(g) and Cl2(g), respectively, the unbalanced chemical equation is
H2(g) + Cl2(g) → HCl(g)Fractional coefficients are required in this case because ΔHof values are reported for 1 mol of the product, HCl. Multiplying both H2(g) and Cl2(g) by 1/2 balances the equation:
\( \dfrac{1}{2}H_{2}\left ( g \right )+ \dfrac{1}{2}Cl_{2}\left ( g \right ) \)\rightarrow HCl\left ( g \right ) \) -
The standard states of the elements in this compound are Mg(s), C(s, graphite), and O2(g). The unbalanced chemical equation is thus
Mg(s) + C(s, graphite) + O2(g) → MgCO3(s)This equation can be balanced by inspection to give
\( Mg\left ( g \right )+ C\left ( s, graphite \right ) \frac{3}{2}O_{2}\left ( g \right )\rightarrow MgCO_{3}\left ( s \right ) \) -
Palmitic acid, the major fat in meat and dairy products, contains hydrogen, carbon, and oxygen, so the unbalanced chemical equation for its formation from the elements in their standard states is as follows:
C(s, graphite) + H2(g) + O2(g) → CH3(CH2)14CO2H(s)There are 16 carbon atoms and 32 hydrogen atoms in 1 mol of palmitic acid, so the balanced chemical equation is
16C(s, graphite) + 16H2(g) + O2(g) → CH3(CH2)14CO2H(s)
Exercise
For the formation of each compound, write a balanced chemical equation corresponding to the standard enthalpy of formation of each compound.
- NaCl(s)
- H2SO4(l)
- CH3CO2H(l) (acetic acid)
Answer:
- \( Na\left ( g \right )+ \frac{1}{2}Cl_{2}\left ( g \right )\rightarrow NaCl\left ( s \right ) \)
- \( H_{2}\left ( g \right ) + \frac{1}{8}S_{8}\left ( s \right ) + 2O_{2}\left ( g \right ) \rightarrow H_{2}SO_{4}\left ( l \right ) \)
- 2C(s) + O2(g) + 2H2(g) → CH3CO2H(l)
Standard Enthalpies of Reaction
Tabulated values of standard enthalpies of formation can be used to calculate enthalpy changes for any reaction involving substances whose ΔHfo values are known. The standard enthalpy of reaction (ΔHrxn)The enthalpy change that occurs when a reaction is carried out with all reactants and products in their standard state. is the enthalpy change that occurs when a reaction is carried out with all reactants and products in their standard states. Consider the general reaction
\( aA + bB \rightarrow cC + dD \tag{15.5.3}\)
where A, B, C, and D are chemical substances and a, b, c, and d are their stoichiometric coefficients. The magnitude of ΔHο is the sum of the standard enthalpies of formation of the products, each multiplied by its appropriate coefficient, minus the sum of the standard enthalpies of formation of the reactants, also multiplied by their coefficients:
\( \begin{matrix} \Delta H_{rxn}^{o} = \left [c\Delta H_{f}^{o}\left ( C \right ) + d\Delta H_{f}^{o}\left ( D \right ) \right ] - & \left [a\Delta H_{f}^{o}\left ( A \right ) + b\Delta H_{f}^{o}\left ( B \right ) \right ] \\ reactants & products \end{matrix} \tag{15.5.4} \)
More generally, we can write
where the symbol Σ means “sum of” and m and n are the stoichiometric coefficients of each of the products and the reactants, respectively. “Products minus reactants” summations such as Equation 15.5.5 arise from the fact that enthalpy is a state function. Because many other thermochemical quantities are also state functions, “products minus reactants” summations are very common in chemistry; we will encounter many others in subsequent chapters.
Note the Pattern
Products minus reactants” summations are typical of state functions.
To demonstrate the use of tabulated ΔHο values, we will use them to calculate ΔHrxn for the combustion of glucose, the reaction that provides energy for your brain:
\( C_{6}H_{12}O_{6} \left ( s \right ) + O_{2}\left ( g \right ) \rightarrow CO_{2}\left ( g \right ) + 6H_{2}O\left ( l \right ) \tag{15.5.6} \)
Using Equation 15.5.5, we write
\( \Delta H_{f}^{o} =\left \{ 6\Delta H_{f}^{o}\left [ CO_{2}\left ( g \right ) \right ] + 6\Delta H_{f}^{o}\left [ H_{2}O\left ( g \right ) \right ] \right \} - \left \{ 6\Delta H_{f}^{o}\left [ C_{6}H_{12}O_{6}\left ( s \right ) \right ] + 6\Delta H_{f}^{o}\left [ O_{2}\left ( g \right ) \right ] \right \} \tag{15.5.7} \)
From the Reference Tables, the relevant ΔHοf values are ΔHοf [CO2(g)] = -393.5 kJ/mol, ΔHοf [H2O(l)] = -285.8 kJ/mol, and ΔHοf [C6H12O6(s)] = -1273.3 kJ/mol. Because O2(g) is a pure element in its standard state, ΔHοf [O2(g)] = 0 kJ/mol. Inserting these values into Equation 15.5.7 and changing the subscript to indicate that this is a combustion reaction, we obtain
\( \begin{matrix} \Delta H_{comb}^{o} = \left [ 6\left ( -393.5 \; kJ/mol \right ) + 6 \left ( -285.8 \; kJ/mol \right ) \right ] \\ - \left [-1273.3 + 6\left ( 0 \; kJ/mol \right ) \right ] = -2802.5 \; kJ/mol \end{matrix} \tag{15.5.8} \)
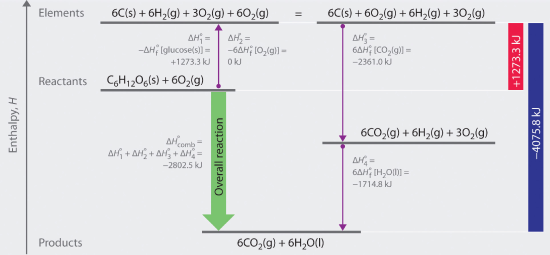
As illustrated in Figure 15.5.2 , we can use Equation 15.5.8 to calculate ΔHοf for glucose because enthalpy is a state function. The figure shows two pathways from reactants (middle left) to products (bottom). The more direct pathway is the downward green arrow labeled ΔHοcomb The alternative hypothetical pathway consists of four separate reactions that convert the reactants to the elements in their standard states (upward purple arrow at left) and then convert the elements into the desired products (downward purple arrows at right). The reactions that convert the reactants to the elements are the reverse of the equations that define the ΔHοf values of the reactants. Consequently, the enthalpy changes are
\( \begin{matrix} \Delta H_{1}^{o} = \Delta H_{f}^{o} \left [ glucose \left ( s \right ) \right ] = -1 \; \cancel{mol \; glucose}\left ( \frac{1273.3 \; kJ}{1 \; \cancel{mol \; glucose}} \right ) = +1273.3 \; kJ \\ \Delta H_{2}^{o} = 6 \Delta H_{f}^{o} \left [ O_{2} \left ( g \right ) \right ] = 6 \; \cancel{mol \; O_{2}}\left ( \frac{0 \; kJ}{1 \; \cancel{mol \; O_{2}}} \right ) = 0 \; kJ \end{matrix} \tag{15.5.9} \)
(Recall that when we reverse a reaction, we must also reverse the sign of the accompanying enthalpy change.) The overall enthalpy change for conversion of the reactants (1 mol of glucose and 6 mol of O2) to the elements is therefore +1273.3 kJ.
Figure 15.5.2 A Thermochemical Cycle for the Combustion of Glucose Two hypothetical pathways are shown from the reactants to the products. The green arrow labeled ΔHοcomb indicates the combustion reaction. Alternatively, we could first convert the reactants to the elements via the reverse of the equations that define their standard enthalpies of formation (the upward arrow, labeled ΔHο1 and ΔHο2 ). Then we could convert the elements to the products via the equations used to define their standard enthalpies of formation (the downward arrows, labeled ΔHο3 and ΔHο4 ). Because enthalpy is a state function, ΔHοcomb is equal to the sum of the enthalpy changes ΔHο1 + ΔHο2 + ΔHο3 + ΔHο4.
The reactions that convert the elements to final products (downward purple arrows in Figure 15.5.2 ) are identical to those used to define the ΔHοf values of the products. Consequently, the enthalpy changes (from the Reference Tables) are
\( \begin{matrix} \Delta H_{3}^{o} = \Delta H_{f}^{o} \left [ CO_{2} \left ( g \right ) \right ] = 6 \; \cancel{mol \; CO_{2}}\left ( \dfrac{393.5 \; kJ}{1 \; \cancel{mol \; CO_{2}}} \right ) = -2361.0 \; kJ \\ \Delta H_{4}^{o} = 6 \Delta H_{f}^{o} \left [ H_{2}O \left ( l \right ) \right ] = 6 \; \cancel{mol \; H_{2}O}\left ( \dfrac{-285.8 \; kJ}{1 \; \cancel{mol \; H_{2}O}} \right ) = -1714.8 \; kJ \end{matrix} \)
The overall enthalpy change for the conversion of the elements to products (6 mol of carbon dioxide and 6 mol of liquid water) is therefore −4075.8 kJ. Because enthalpy is a state function, the difference in enthalpy between an initial state and a final state can be computed using any pathway that connects the two. Thus the enthalpy change for the combustion of glucose to carbon dioxide and water is the sum of the enthalpy changes for the conversion of glucose and oxygen to the elements (+1273.3 kJ) and for the conversion of the elements to carbon dioxide and water (−4075.8 kJ):
\( \Delta H_{comb}^{o} = +1273.3 \; kJ +\left ( -4075.8 \; kJ \right ) = -2802.5 \; kJ \tag{15.5.10} \)
This is the same result we obtained using the “products minus reactants” rule and ΔHοf values. The two results must be the same because Equation 15.5.10 is just a more compact way of describing the thermochemical cycle shown in Figure 15.5.2.
Example 15.5.2
Long-chain fatty acids such as palmitic acid [CH3(CH2)14CO2H] are one of the two major sources of energy in our diet (ΔHοf =−891.5 kJ/mol). Use the data in the Reference Table to calculate ΔHοcomb for the combustion of palmitic acid. Based on the energy released in combustion per gram, which is the better fuel — glucose or palmitic acid?
Given: compound and ΔHοf values
Asked for: ΔHοcomb per mole and per gram
Strategy:
A After writing the balanced chemical equation for the reaction, use Equation 15.5.5 and the values from the Reference Table to calculate ΔHοcomb the energy released by the combustion of 1 mol of palmitic acid.
B Divide this value by the molar mass of palmitic acid to find the energy released from the combustion of 1 g of palmitic acid. Compare this value with the value calculated in Equation 15.5.8 for the combustion of glucose to determine which is the better fuel.
Solution:
A To determine the energy released by the combustion of palmitic acid, we need to calculate its ΔHοf As always, the first requirement is a balanced chemical equation:
C16H32O2(s) + 23O2(g) → 16CO2(g) + 16H2O(l)
Using Equation 15.5.5 (“products minus reactants”) with ΔHοf values from the Reference Table (and omitting the physical states of the reactants and products to save space) gives
\( \Delta H_{comb}^{o} = \sum m \Delta {H^o}_f\left( {products} \right) - \sum n \Delta {H^o}_f\left( {reactants} \right) \)
\( = \left [ 16\left ( -393.5 \; kJ/mol \; CO_{2} \right ) + 16\left ( -285.8 \; kJ/mol \; H_{2}O \; \right ) \right ] \)
\( - \left [ -891.5 \; kJ/mol \; C_{16}H_{32}O_{2} + 23\left ( 0 \; kJ/mol \; O_{2} \; \right ) \right ] \)
\( = -9977.3 \; kJ/mol \)
This is the energy released by the combustion of 1 mol of palmitic acid.
B The energy released by the combustion of 1 g of palmitic acid is
\( \Delta H_{comb}^{o} \; per \; gram =\left ( \dfrac{9977.3 \; kJ}{\cancel{1 \; mol}} \right ) \left ( \dfrac{\cancel{1 \; mol}}{256.42 \; g} \right )= -38.910 \; kJ/g \)
As calculated in Equation 15.5.8, ΔHοf of glucose is −2802.5 kJ/mol. The energy released by the combustion of 1 g of glucose is therefore
\( \Delta H_{comb}^{o} \; per \; gram =\left ( \dfrac{-2802.5 \; kJ}{\cancel{1\; mol}} \right ) \left ( \dfrac{\cancel{1 \; mol}}{180.16\; g} \right ) = -15.556 \; kJ/g \)
The combustion of fats such as palmitic acid releases more than twice as much energy per gram as the combustion of sugars such as glucose. This is one reason many people try to minimize the fat content in their diets to lose weight.
Exercise
Use the data in the Reference Tables to calculate ΔHοrxn for the water–gas shift reaction, which is used industrially on an enormous scale to obtain H2(g):
\( \begin{pmatrix}
CO\left ( g \right )+H_{2}O\left ( g \right )\rightarrow CO_{2} \left ( g \right )+H_{2}\left ( g \right ) \\
water-gas \; shift \; reaction
\end{pmatrix} \)
Answer: −41.2 kJ/mol
We can also measure the enthalpy change for another reaction, such as a combustion reaction, and then use it to calculate a compound’s ΔHοf which we cannot obtain otherwise. This procedure is illustrated in Example 3.
Example 15.5.3
Beginning in 1923, tetraethyllead [(C2H5)4Pb] was used as an antiknock additive in gasoline in the United States. Its use was completely phased out in 1986 because of the health risks associated with chronic lead exposure. Tetraethyllead is a highly poisonous, colorless liquid that burns in air to give an orange flame with a green halo. The combustion products are CO2(g), H2O(l), and red PbO(s). What is the standard enthalpy of formation of tetraethyllead, given that ΔHοf is −19.29 kJ/g for the combustion of tetraethyllead and ΔHοf of red PbO(s) is −219.0 kJ/mol?
Given: reactant, products, and ΔHοcomb values
Asked for: ΔHοf of the reactants
Strategy:
A Write the balanced chemical equation for the combustion of tetraethyl lead. Then insert the appropriate quantities into Equation 5.27 to get the equation for ΔHοf of tetraethyl lead.
B Convert ΔHοcomb per gram given in the problem to ΔHοcomb per mole by multiplying ΔHοcomb per gram by the molar mass of tetraethyllead.
C Use the Reference Table to obtain values of ΔHοf for the other reactants and products. Insert these values into the equation for ΔHοf of tetraethyl lead and solve the equation.
Solution:
A The balanced chemical equation for the combustion reaction is as follows:
2(C2H5)4Pb(l) + 27O2(g) → 2PbO(s) + 16CO2(g) + 20H2O(l)
Using Equation 15.5.5 gives
\( \Delta H_{comb}^{o} = \left [ 2 \Delta H_{f}^{o}\left ( PbO \right ) + 16 \Delta H_{f}^{o}\left ( CO_{2} \right ) + 20 \Delta H_{f}^{o}\left ( H_{2}O \right )\right ] - \left [2 \Delta H_{f}^{o}\left ( \left ( C_{2}H_{5} \right ) _{4} Pb \right ) + 27 \Delta H_{f}^{o}\left ( O_{2} \right ) \right ] \)
Solving for ΔHοf [(C2H5)4Pb] gives
\( \Delta H_{f}^{o}\left ( \left ( C_{2}H_{5} \right ) _{4} Pb \right ) = \Delta H_{f}^{o}\left ( PbO \right ) + 8 \Delta H_{f}^{o}\left ( CO_{2} \right ) + 10 \Delta H_{f}^{o}\left ( H_{2}O \right ) - \frac{27}{2} \Delta H_{f}^{o}\left ( O_{2} \right ) - \frac{\Delta H_{comb}^{o}}{2} \)
The values of all terms other than ΔHοf [(C2H5)4Pb] are given in the Reference Table
B The magnitude of ΔHοcomb is given in the problem in kilojoules per gram of tetraethyl lead. We must therefore multiply this value by the molar mass of tetraethyl lead (323.44 g/mol) to get ΔHοcomb for 1 mol of tetraethyl lead:
\( \Delta H_{comb}^{o} = \left ( \dfrac{-1929 \; kJ}{\cancel{g}} \right )\left ( \dfrac{323.44 \; \cancel{g}}{mol} \right ) = -6329 \; kJ/mol \)
Because the balanced chemical equation contains 2 mol of tetraethyllead, ΔHοrxn is
\( \Delta H_{rxn}^{o} = 2 \; \cancel{mol \; \left ( C_{2}H{5}\right )_4 Pb} \left ( \frac{-6929 \; kJ}{1 \; \cancel{mol \; \left ( C_{2}H{5}\right )_4 Pb }} \right ) = -12,480 \; kJ \)
C Inserting the appropriate values into the equation for ΔHοf [(C2H5)4Pb] gives
\( \begin{matrix}
\Delta H_{f}^{o} \left [ \left (C_{2}H_{4} \right )_{4}Pb \right ] & = & \left [1 \; mol \;PbO \;\times 219.0 \;kJ/mol \right ]+\left [8 \; mol \;CO_{2} \times \left (-393.5 \; kJ/mol \right )\right ] \\
& & +\left [10 \; mol \; H_{2}O \times \left ( -285.8 \; kJ/mol \right )\right ] + \left [-27/2 \; mol \; O_{2}) \times 0 \; kJ/mol \; O_{2}\right ] \\
& & \left [12,480.2 \; kJ/mol \; \left ( C_{2}H_{5} \right )_{4}Pb \right ]\\
& = & -219.0 \; kJ -3148 \; kJ - 2858 kJ - 0 kJ + 6240 \; kJ = 15 kJ/mol
\end{matrix} \)
Exercise
Ammonium sulfate [(NH4)2SO4] is used as a fire retardant and wood preservative; it is prepared industrially by the highly exothermic reaction of gaseous ammonia with sulfuric acid:
2NH3(g) + H2SO4(aq) → (NH4)2SO4(s)
The value of ΔHorxn is −2805 kJ/g H2SO4. Use the data in Appendix A to calculate the standard enthalpy of formation of ammonium sulfate (in kilojoules per mole).
Answer: −1181 kJ/mol
Key Equations
relationship between ΔHorxn and ΔHοf
Equation 15.5.5: ΔHorxn = ΣΔHof(products) −ΔHof(reactants)
Summary
The enthalpy of formation (ΔHf) is the enthalpy change that accompanies the formation of a compound from its elements. Standard enthalpies of formation (ΔHof) are determined under standard conditions: a pressure of 1 atm for gases and a concentration of 1 M for species in solution, with all pure substances present in their standard states (their most stable forms at 1 atm pressure and the temperature of the measurement). The standard heat of formation of any element in its most stable form is defined to be zero. The standard enthalpy of reaction (ΔHorxn) can be calculated from the sum of the standard enthalpies of formation of the products (each multiplied by its stoichiometric coefficient) minus the sum of the standard enthalpies of formation of the reactants (each multiplied by its stoichiometric coefficient)—the “products minus reactants” rule. The enthalpy of solution (ΔHsoln) is the heat released or absorbed when a specified amount of a solute dissolves in a certain quantity of solvent at constant pressure.
Key Takeaways
- The standard state for measuring and reporting enthalpies of formation or reaction is 25 oC and 1 atm.
- The elemental form of each atom is that with the lowest enthalpy in the standard state.
- The standard state heat of formation for the elemental form of each atom is zero.
Conceptual Problems
-
Describe how Hess’s law can be used to calculate the enthalpy change of a reaction that cannot be observed directly.
-
When you apply Hess’s law, what enthalpy values do you need to account for each change in physical state?
-
What is the difference between ΔHof and ΔHf?
-
How can ΔHof of a compound be determined if the compound cannot be prepared by the reactions used to define its standard enthalpy of formation?
-
For the formation of each compound, write a balanced chemical equation corresponding to the standard enthalpy of formation of each compound.
a. HBr
b. CH3OH
c. NaHCO3
-
Describe the distinction between ΔHsoln and ΔHf.
-
The following table lists ΔHosoln values for some ionic compounds. If 1 mol of each solute is dissolved in 500 mL of water, rank the resulting solutions from warmest to coldest.
Compound ΔHosoln(kJ/mol) KOH −57.61 LiNO3 −2.51 KMnO4 43.56 NaC2H3O2 −17.32
Numerical Problems
-
Using "Appendix A, calculate ΔHorxn for each chemical reaction.
a. 2Mg(s) + O2(g) → 2MgO(s)
b. CaCO3(s, calcite) → CaO(s) + CO2(g)
c. AgNO3(s) + NaCl(s) → AgCl(s) + NaNO3(s)
-
Using "Appendix A, determine ΔHorxn for each chemical reaction.
a. 2Na(s) + Pb(NO3)2(s) → 2NaNO3(s) + Pb(s)
b. Na2CO3(s) + H2SO4(l) → Na2SO4(s) + CO2(g) + H2O(l)
c. 2KClO3(s) → 2KCl(s) + 3O2(g)
-
Calculate ΔHorxn for each chemical equation. If necessary, balance the chemical equations.
a. Fe(s) + CuCl2(s) → FeCl2(s) + Cu(s)
b. (NH4)2SO4(s) + Ca(OH)2(s) → CaSO4(s) + NH3(g) + H2O(l)
c. Pb(s) + PbO2(s) + H2SO4(l) → PbSO4(s) + H2O(l)
-
Calculate ΔHorxn for each reaction. If necessary, balance the chemical equations.
a. 4HBr(g) + O2(g) → 2H2O(l) + 2Br2(l)
b. 2KBr(s) + H2SO4(l) → K2SO4(s) + 2HBr(g)
c. 4Zn(s) + 9HNO3(l) → 4Zn(NO3)2(s) + NH3(g) + 3H2O(l)
-
Use the data in "Appendix A to calculate ΔHof for the reaction Sn(s, white) + 4HNO3(l) → SnO2(s) + 4NO2(g) + 2H2O(l).
-
Use the data in "Appendix A to calculate ΔHof for the reaction P4O10(s) + 6H2O(l) → 4H3PO4(l).
-
How much heat is released or required in the reaction of 0.50 mol of HBr(g) with 1.0 mol of chlorine gas to produce bromine gas?
-
How much energy is released or consumed if 10.0 g of N2O5 is completely decomposed to produce gaseous nitrogen dioxide and oxygen?
-
In the mid-1700s, a method was devised for preparing chlorine gas from the following reaction:
NaCl(s) + H2SO4(l) + MnO2(s) → Na2SO4(s) + MnCl2(s) + H2O(l) + Cl2(g)
Calculate ΔHorxn for this reaction. Is the reaction exothermic or endothermic?
-
Would you expect heat to be evolved during each reaction?
- solid sodium oxide with gaseous sulfur dioxide to give solid sodium sulfite
- solid aluminum chloride reacting with water to give solid aluminum oxide and hydrogen chloride gas
-
How much heat is released in preparing an aqueous solution containing 6.3 g of calcium chloride, an aqueous solution containing 2.9 g of potassium carbonate, and then when the two solutions are mixed together to produce potassium chloride and calcium carbonate?
-
Answers
-
a. −1203 kJ/mol O2
b. 179.2 kJ
c. −59.3 kJ
-
−174.1 kJ/mol
-
−20.3 kJ
-
−34.3 kJ/mol Cl2; exothermic
-
ΔH = −2.86 kJ CaCl2: −4.6 kJ; K2CO3, −0.65 kJ; mixing, −0.28 kJ
Contributors
- Anonymous
Modified by Joshua Halpern (Howard University), Scott Sinex, and Scott Johnson (PGCC)