Chapter 9.7: End of Chapter Materials
- Page ID
- 42105
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\) |
Prince George's Community College |
 |
| Unit I: Atoms Unit II: Molecules Unit III: States of Matter Unit IV: Reactions Unit V: Kinetics & Equilibrium Unit VI: Thermo & Electrochemistry Unit VII: Nuclear Chemistry |
||
Problems
Problems marked with a ♦ involve multiple concepts.
-
♦ Scuba divers utilize high-pressure gas in their tanks to allow them to breathe under water. At depths as shallow as 100 ft (30 m), the pressure exerted by water is 4.0 atm. At 25°C the values of Henry’s law constants for N2, O2, and He in blood are as follows: N2 = 6.5 × 10−4 mol/(L·atm), O2 = 1.28 × 10−3 mol/(L·atm), and He = 3.7 × 10−4 mol/(L·atm).
- What would be the concentration of nitrogen and oxygen in blood at sea level where the air is 21% oxygen and 79% nitrogen?
- What would be the concentration of nitrogen and oxygen in blood at a depth of 30 m, assuming that the diver is breathing compressed air?
-
♦ Many modern batteries take advantage of lithium ions dissolved in suitable electrolytes. Typical batteries have lithium concentrations of 0.10 M. Which aqueous solution has the higher concentration of ion pairs: 0.08 M LiCl or 1.4 M LiCl? Why? Does an increase in the number of ion pairs correspond to a higher or lower van’t Hoff factor? Batteries rely on a high concentration of unpaired Li+ ions. Why is using a more concentrated solution not an ideal strategy in this case?
-
Hydrogen sulfide, which is extremely toxic to humans, can be detected at a concentration of 2.0 ppb. At this level, headaches, dizziness, and nausea occur. At higher concentrations, however, the sense of smell is lost, and the lack of warning can result in coma and death can result. What is the concentration of H2S in milligrams per liter at the detection level? The lethal dose of hydrogen sulfide by inhalation for rats is 7.13 × 10−4 g/L. What is this lethal dose in ppm? The density of air is 1.2929 g/L.
-
One class of antibiotics consists of cyclic polyethers that can bind alkali metal cations in aqueous solution. Given the following antibiotics and cation selectivities, what conclusion can you draw regarding the relative sizes of the cavities?
Antibiotic Cation Selectivity nigericin K+ > Rb+ > Na+ > Cs+ > Li+ lasalocid Ba2+ >> Cs+ > Rb+, K+ > Na+, Ca2+, Mg2+ -
Phenylpropanolamine hydrochloride is a common nasal decongestant. An aqueous solution of phenylpropanolamine hydrochloride that is sold commercially as a children’s decongestant has a concentration of 6.67 × 10−3 M. If a common dose is 1.0 mL/12 lb of body weight, how many moles of the decongestant should be given to a 26 lb child?
-
The “freeze-thaw” method is often used to remove dissolved oxygen from solvents in the laboratory. In this technique, a liquid is placed in a flask that is then sealed to the atmosphere, the liquid is frozen, and the flask is evacuated to remove any gas and solvent vapor in the flask. The connection to the vacuum pump is closed, the liquid is warmed to room temperature and then refrozen, and the process is repeated. Why is this technique effective for degassing a solvent?
-
Suppose that, on a planet in a galaxy far, far away, a species has evolved whose biological processes require even more oxygen than we do. The partial pressure of oxygen on this planet, however, is much less than that on Earth. The chemical composition of the “blood” of this species is also different. Do you expect their “blood” to have a higher or lower value of the Henry’s law constant for oxygen at standard temperature and pressure? Justify your answer.
-
A car owner who had never taken general chemistry decided that he needed to put some ethylene glycol antifreeze in his car’s radiator. After reading the directions on the container, however, he decided that “more must be better.” Instead of using the recommended mixture (30% ethylene glycol/70% water), he decided to reverse the amounts and used a 70% ethylene glycol/30% water mixture instead. Serious engine problems developed. Why?
-
The ancient Greeks produced “Attic ware,” pottery with a characteristic black and red glaze. To separate smaller clay particles from larger ones, the powdered clay was suspended in water and allowed to settle. This process yielded clay fractions with coarse, medium, and fine particles, and one of these fractions was used for painting. Which size of clay particles forms a suspension, which forms a precipitate, and which forms a colloidal dispersion? Would the colloidal dispersion be better characterized as an emulsion? Why or why not? Which fraction of clay particles was used for painting?
-
The Tyndall effect is often observed in movie theaters, where it makes the beam of light from the projector clearly visible. What conclusions can you draw about the quality of the air in a movie theater where you observe a large Tyndall effect?
-
Aluminum sulfate is the active ingredient in styptic pencils, which can be used to stop bleeding from small cuts. The Al3+ ions induce aggregation of colloids in the blood, which facilitates formation of a blood clot. How can Al3+ ions induce aggregation of a colloid? What is the probable charge on the colloidal particles in blood?
-
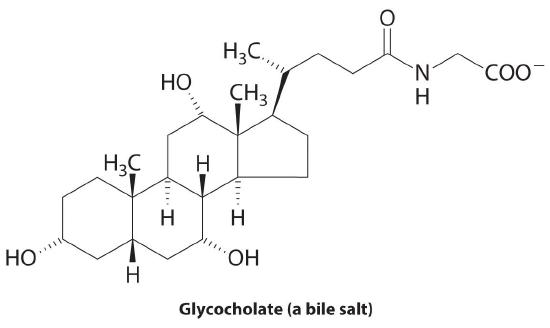
♦ The liver secretes bile, which is essential for the digestion of fats. Fats are biomolecules with long hydrocarbon chains. The globules of fat released by partial digestion of food particles in the stomach and lower intestine are too large to be absorbed by the intestine unless they are emulsified by bile salts, such as glycocholate. Explain why a molecule like glycocholate is effective at creating an aqueous dispersion of fats in the digestive tract.
Answers
-
- 1 atm: 2.7 × 10−4 M O2 and 5.1 × 10−4 M N2
- 4 atm: 1.1 × 10−3 M O2 and 2.1 × 10−3 M N2
-
-
2.6 × 10−6 mg/L, 550 ppm
-
-
1.4 × 10−5 mol
-
-
To obtain the same concentration of dissolved oxygen in their “blood” at a lower partial pressure of oxygen, the value of the Henry’s law constant would have to be higher.
-
-
The large, coarse particles would precipitate, the medium particles would form a suspension, and the fine ones would form a colloid. A colloid consists of solid particles in a liquid medium, so it is not an emulsion, which consists of small particles of one liquid suspended in another liquid. The finest particles would be used for painting.
-
-
-
Contributors
- Anonymous