Chapter 1.3: The Nucleus and Radioactivity
- Page ID
- 37499
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\) |
Prince George's Community College |
 |
| Unit I: Atoms Unit II: Molecules Unit III: States of Matter Unit IV: Reactions Unit V: Kinetics & Equilibrium Unit VI: Thermo & Electrochemistry Unit VII: Nuclear Chemistry |
||
Learning Objective
- To know the meaning of isotopes and atomic masses.
We know about four forces in the universe. Gravity is a very weak force that functions on the scale of galaxies as well as apples falling. Gravitational effects are only obvious for very large objects, such as the Earth, the Sun, galaxies and the universe. There is little to nothing in chemistry where we have to include gravity in our analysis, well other than in how we weigh chemicals.
Most chemical phenomina are controlled by electromagnetic forces. The typical distances involved in the interactions of these charged particles are a billionth of a meter.
The weak and strong forces are forces holding nuclei together. These forces are studied by nuclear and high energy physicists. Their range is much smaller than the electromagnetic force, in the case of the weak interaction 10-17 m, roughly the size of the atomic nucleus.
The strong force, is short range, but also very strong. It is what holds atomic nuclei together and confines quarks in nuclear particles such as protons and neutrons. Again, like gravitation, there is very little in chemistry where we need to consider the strong and weak forces in our analysis except for nuclear reactions.
Nuclear reactions differ from chemical processes in one critical way: in a nuclear reaction, the identities of the elements change. In addition, nuclear reactions are often accompanied by the release of enormous amounts of energy, as much as a billion times more than the energy released by chemical reactions. Moreover, the yields and rates of a nuclear reaction are generally unaffected by changes in temperature, pressure, because the energy associated with a change in temperature or pressure is miniscule compared to the energies of nuclear reaction
We all know about E=mc2. Einstein discovered that mass and energy are related. However the amount of energy released in conversion of even the tiniest amount of mass to energy is far beyond normal chemistry. For practical purposes atoms (mass) are not transmuted either into other types of atoms or to pure energy. We can and do do this in nuclear reactors, atom smashers and atomic weapons, however, these are not normal, everyday chemistry, and the energy range involved in nuclear chemistry and such processes is well beyond common experience and this course.
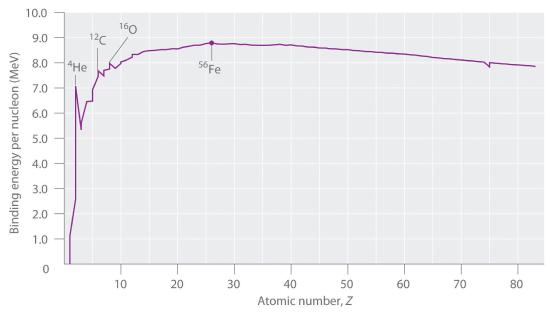
The amount of mass converted into binding energy varies across the periodic table. As shown in Figure 1.3.1 the binding energy per nucleon increases rapidly with increasing atomic number until about Z = 26, where it levels off to about 8–9 MeV per nucleon and then decreases slowly. The initial increase in binding energy is not a smooth curve but exhibits sharp peaks corresponding to the light nuclei that have equal numbers of protons and neutrons (e.g., 4He, 12C, and 16O). As mentioned earlier, these are particularly stable combinations.
Figure 1.3.1 The Curve of Nuclear Binding Energy This plot of the average binding energy per nucleon as a function of atomic number shows that the binding energy per nucleon increases with increasing atomic number until about Z = 26, levels off, and then decreases. The sharp peaks correspond to light nuclei that have equal numbers of protons and neutrons.
Because the maximum binding energy per nucleon is reached at 56Fe, all other nuclei are thermodynamically unstable with regard to the formation of 56Fe. Most elements have a number of isotopes but only a few that are stable. The rest decay spontaneously either by spitting out an electron, called a β particle, a helium nucleus, called an \( \alpha \) particle, a neutron or a high energy photon, also called a \( \gamma \). Heavier nuclei (toward the right in Figure 1.3.1 ) could spontaneously undergo reactions that decrease their atomic number by emitting an \( \alpha \) particle which consists of two protons and four neutrons. If this happens the atomic number of the nucleus decreases by two, equivalent to moving to the left in Figure 1.3.1. Conversely, lighter elements (on the left in Figure 1.3.1) should spontaneously undergo reactions that result in an increase in atomic number by converting a neutron to a proton and an electron an emitting the electron. When this happens to conserve momentum a neutrino (don't ask in this class) is also emitted. If a neutron is emitted /absorbed then the atomic number stays the same, but the resulting isotope has one less or more neutron.
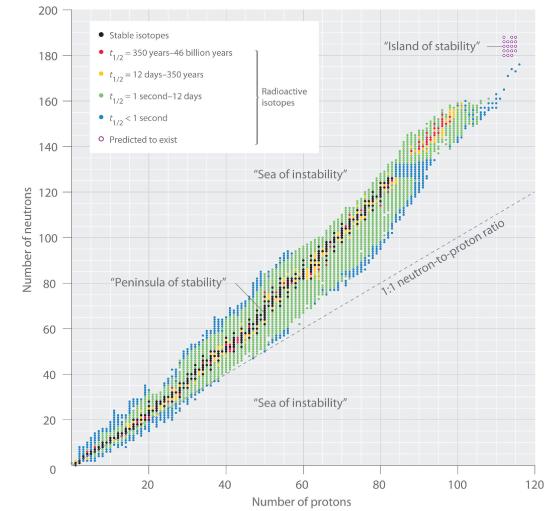
Figure 1.3.2 The Relationship between Nuclear Stability and the Neutron-to-Proton Ratio In this plot of the number of neutrons versus the number of protons, each black point corresponds to a stable nucleus. In this classification, a stable nucleus is arbitrarily defined as one with a half-life longer than 46 billion years (10 times the age of Earth). As the number of protons (the atomic number) increases, the number of neutrons required for a stable nucleus increases even more rapidly. Isotopes shown in red, yellow, green, and blue are progressively less stable and more radioactive; the farther an isotope is from the diagonal band of stable isotopes, the shorter its half-life. The purple dots indicate superheavy nuclei that are predicted to be relatively stable, meaning that they are expected to be radioactive but to have relatively long half-lives. In most cases, these elements have not yet been observed or synthesized.
Data source: National Nuclear Data Center, Brookhaven National Laboratory, Evaluated Nuclear Structure Data File (ENSDF), Chart of Nuclides, http://www.nndc.bnl.gov/chart. This is an interactive chart
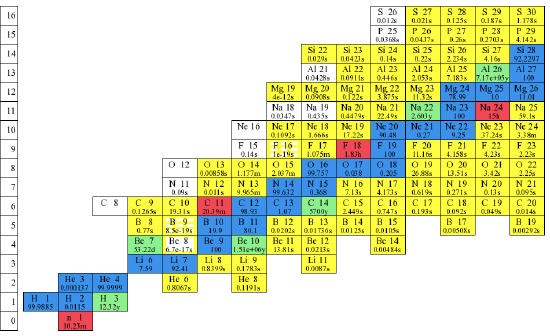
Looking at Figure 1.3.2 we see how the number of neutrons increases faster than the number of protons in stable and even in unstable (radioactive) isotopes. No isotopes in the sea of instability have been observed. If they could be made, they would simply decay too quickly to be seen. Figure 1.3.3 shows the lower part of the table with the various elements and their isotopes identified. The times listed at the bottom of the box for unstable isotopes is the time in which half of any sample undergo nuclear reaction. This is called the half life and we will discuss it in the chapter on kinetics.
Figure 1.3.3 Observed isotopes of the elements from Hydrogen to Sulfur(partial). Stable isotopes are shown in blue. Lifetimes of unstable isotopes shown in green, yellow, pink and white are indicated at the bottom of each box. Note that naked neutrons decay to a proton and an electron in about 10 minutes.
Contributors►
- Anonymous
Modified by Joshua Halpern, Scott Sinex and Scott Johnson
Interactive table of nuclides from National Nuclear Data Center, Brookhaven National Laboratory, Evaluated Nuclear Structure Data File (ENSDF)