Chapter 1.2: Isotopes and Atomic Masses
- Page ID
- 19868
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\) |
Prince George's Community College |
 |
| Unit I: Atoms Unit II: Molecules Unit III: States of Matter Unit IV: Reactions Unit V: Kinetics & Equilibrium Unit VI: Thermo & Electrochemistry Unit VII: Nuclear Chemistry |
||
Learning Objectives
- To know the meaning of isotopes and atomic masses.
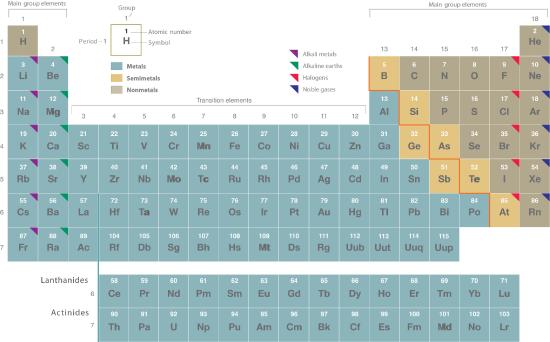
Rutherford’s nuclear model of the atom helped explain why atoms of different elements exhibit different chemical behavior. The identity of an element is defined by its atomic number (Z)The number of protons in the nucleus of an atom of an element., the number of protons in the nucleus of an atom of the element. The atomic number is therefore different for each element. The known elements are arranged in order of increasing Z in the periodic tableA chart of the chemical elements arranged in rows of increasing atomic number so that the elements in each column (group) have similar chemical properties. (Figure 1.2.1 ). We will explain the rationale for the form of the periodic table in Chapter 3 . In the periodic table each element is assigned a unique one-, two-, or three-letter symbol. The names of the elements are listed in the periodic table, along with their symbols, atomic numbers, and atomic masses. The chemistry of each element is determined by its number of protons and electrons. In a neutral atom, the number of electrons equals the number of protons.
Figure 1.2.1 The Periodic Table Showing the Elements in Order of Increasing Z The metals are shown in blue, and the nonmetals are shown in brown. The semimetals lie along a diagonal line separating the metals and nonmetals. In the third chapter we will discover why the table appears as it does.
In most cases, the symbols for the elements are derived directly from each element’s name, such as C for carbon, U for uranium, Ca for calcium, and Po for polonium. Elements have also been named for their properties [such as radium (Ra) for its radioactivity], for the native country of the scientist(s) who discovered them [polonium (Po) for Poland], for eminent scientists [curium (Cm) for the Curies], for gods and goddesses [selenium (Se) for the Greek goddess of the moon, Selene], and for other poetic or historical reasons. Some of the symbols used for elements that have been known since antiquity are derived from historical names that are no longer in use; only the symbols remain to remind us of their origin. Examples are Fe for iron, from the Latin ferrum; Na for sodium, from the Latin natrium; and W for tungsten, from the German wolfram. Examples are in Table 1.2.1 As you work through this text, you will encounter the names and symbols of the elements repeatedly, and much as you become familiar with characters in a play or a film, their names and symbols will become familiar.
Table 1.2.1 Element Symbols Based on Names No Longer in Use
| Element | Symbol | Derivation | Meaning |
|---|---|---|---|
| antimony | Sb | stibium | Latin for “mark” |
| copper | Cu | cuprum | from Cyprium, Latin name for the island of Cyprus, the major source of copper ore in the Roman Empire |
| gold | Au | aurum | Latin for “gold” |
| iron | Fe | ferrum | Latin for “iron” |
| lead | Pb | plumbum | Latin for “heavy” |
| mercury | Hg | hydrargyrum | Latin for “liquid silver” |
| potassium | K | kalium | from the Arabic al-qili, “alkali” |
| silver | Ag | argentum | Latin for “silver” |
| sodium | Na | natrium | Latin for “sodium” |
| tin | Sn | stannum | Latin for “tin” |
| tungsten | W | wolfram | German for “wolf stone” because it interfered with the smelting of tin and was thought to devour the tin |
If you want to learn the names of the elements and how to pronounce them, there is nothing better than a song
Old timers (perhaps your lecturer is the only one in the class) will recognize this as a cover of Tom Lehrer's Song of the Elements
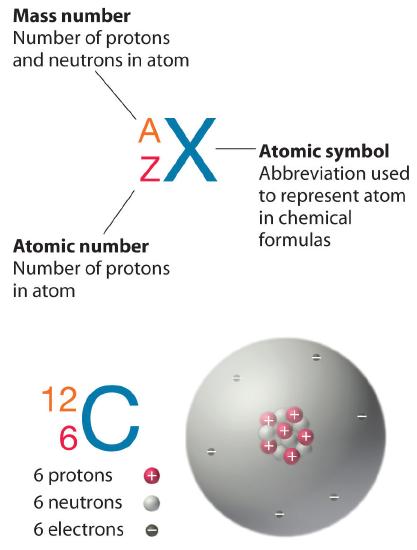
Recall from Section 1.1 that the nuclei of most atoms contain neutrons as well as protons. Unlike protons, the number of neutrons is not absolutely fixed for most elements. Atoms that have the same number of protons, and hence the same atomic number, but different numbers of neutrons are called isotopesAtoms that have the same numbers of protons but different numbers of neutrons. All isotopes of an element have the same number of protons and electrons, which means they exhibit the same chemistry. The isotopes of an element differ only in their atomic mass, which is given by the mass number (A)The number of protons and neutrons in the nucleus of an atom of an element., the sum of the numbers of protons and neutrons.
The element carbon (C) has an atomic number of 6, which means that all neutral carbon atoms contain 6 protons and 6 electrons. In a typical sample of carbon-containing material, 98.89% of the carbon atoms also contain 6 neutrons, so each has a mass number of 12. An isotope of any element can be uniquely represented as \({}_Z^{A}X\)where X is the atomic symbol of the element. The isotope of carbon that has 6 neutrons is therefore \({}_6^{12}C\) The subscript indicating the atomic number is actually redundant because the atomic symbol already uniquely specifies Z. Consequently, it is more often written as 12C, which is read as “carbon-12.” Nevertheless, the value of Z is commonly included in the notation for nuclear reactions because these reactions involve changes in Z.
In addition to 12C, a typical sample of carbon contains 1.11% \({}_6^{13}C\) (13C), with 7 neutrons and 6 protons, and a trace of \({}_6^{14}C\) (14C), with 8 neutrons and 6 protons. The nucleus of 14C is not stable, however, but undergoes a slow radioactive decay that is the basis of the carbon-14 dating technique used in archaeology. Many elements other than carbon have more than one stable isotope; tin, for example, has 10 isotopes. The properties of some common isotopes are in Table 1.2.2 .
Table 1.2.2 Properties of Selected Isotopes
| Element | Symbol | Atomic Mass (amu) | Isotope Mass Number | Isotope Masses (amu) | Percent Abundances (%) |
|---|---|---|---|---|---|
| hydrogen | H | 1.0079 | 1 | 1.007825 | 99.9855 |
| 2 | 2.014102 | 0.0115 | |||
| boron | B | 10.81 | 10 | 10.012937 | 19.91 |
| 11 | 11.009305 | 80.09 | |||
| carbon | C | 12.011 | 12 | 12 (defined) | 99.89 |
| 13 | 13.003355 | 1.11 | |||
| oxygen | O | 15.9994 | 16 | 15.994915 | 99.757 |
| 17 | 16.999132 | 0.0378 | |||
| 18 | 17.999161 | 0.205 | |||
| iron | Fe | 55.845 | 54 | 53.939611 | 5.82 |
| 56 | 55.934938 | 91.66 | |||
| 57 | 56.935394 | 2.19 | |||
| 58 | 57.933276 | 0.33 | |||
| uranium | U | 238.03 | 234 | 234.040952 | 0.0054 |
| 235 | 235.043930 | 0.7204 | |||
| 238 | 238.050788 | 99.274 |
Sources of isotope data: G. Audi et al., Nuclear Physics A 729 (2003): 337–676; J. C. Kotz and K. F. Purcell, Chemistry and Chemical Reactivity, 2nd ed., 1991.
Example 1.2.1
An element with three stable isotopes has 82 protons. The separate isotopes contain 124, 125, and 126 neutrons. Identify the element and write symbols for the isotopes.
Given: number of protons and neutrons
Asked for: element and atomic symbol
Strategy:
A Refer to the periodic table and use the number of protons to identify the element.
B Calculate the mass number of each isotope by adding together the numbers of protons and neutrons.
C Give the symbol of each isotope with the mass number as the superscript and the number of protons as the subscript, both written to the left of the symbol of the element.
Solution:
A The element with 82 protons (atomic number of 82) is lead: Pb.
B For the first isotope, A = 82 protons + 124 neutrons = 206. Similarly, A = 82 + 125 = 207 and A = 82 + 126 = 208 for the second and third isotopes, respectively. The symbols for these isotopes are \({}_{82}^{206}Pb\), \({}_{82}^{207}Pb\) and \({}_{82}^{208}Pb\) which are usually abbreviated as 206Pb, 207Pb, and 208Pb.
Exercise
Identify the element with 35 protons and write the symbols for its isotopes with 44 and 46 neutrons.
Answer: \({}_{35}^{79}Br\) and \({}_{35}^{81}Br\) or, more commonly, 79Br and 81Br.
Although the masses of the electron, the proton, and the neutron are known to a high degree of precision (Table 1.2.2), the mass of any given atom is not simply the sum of the masses of its electrons, protons, and neutrons. For example, the ratio of the masses of 1H (hydrogen) and 2H (deuterium) is actually 0.500384, rather than 0.49979 as predicted from the numbers of neutrons and protons present. Although the difference in mass is small, it is extremely important because it is the binding energy of the nucleus. We can easily calculate the binding energy from the mass difference using Einstein's formula E=mc2.
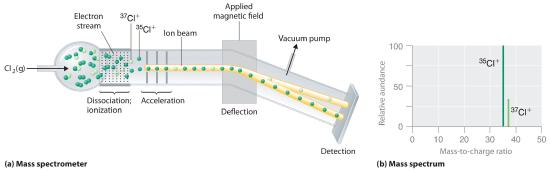
Because atoms are much too small to measure individually and do not have a charge, there is no convenient way to accurately measure absolute atomic masses. Scientists can measure relative atomic masses very accurately, however, using an instrument called a mass spectrometer. The technique is conceptually similar to the one Thomson used to determine the mass-to-charge ratio of the electron. First, electrons are removed from or added to atoms or molecules, thus producing charged particles called ionsA charged particle produced when one or more electrons is removed from or added to an atom or molecule.. When an electric field is applied, the ions are accelerated into a separate chamber where they are deflected from their initial trajectory by a magnetic field, like the electrons in Thomson’s experiment. The extent of the deflection depends on the mass-to-charge ratio of the ion. By measuring the relative deflection of ions that have the same charge, scientists can determine their relative masses (Figure 1.2.2). Thus it is not possible to calculate absolute atomic masses accurately by simply adding together the masses of the electrons, the protons, and the neutrons, and absolute atomic masses cannot be measured, but relative masses can be measured very accurately. It is actually rather common in chemistry to encounter a quantity whose magnitude can be measured only relative to some other quantity, rather than absolutely. We will encounter many other examples later in this text. In such cases, chemists usually define a standard by arbitrarily assigning a numerical value to one of the quantities, which allows them to calculate numerical values for the rest.
Figure 1.2.2 Determining Relative Atomic Masses Using a Mass Spectrometer Chlorine consists of two isotopes, 35Cl and 37Cl, in approximately a 3:1 ratio. (a) When a sample of elemental chlorine is injected into the mass spectrometer, electrical energy is used to dissociate the Cl2 molecules into chlorine atoms and convert the chlorine atoms to Cl+ ions. The ions are then accelerated into a magnetic field. The extent to which the ions are deflected by the magnetic field depends on their relative mass-to-charge ratios. Note that the lighter 35Cl+ ions are deflected more than the heavier 37Cl+ ions. By measuring the relative deflections of the ions, chemists can determine their mass-to-charge ratios and thus their masses. (b) Each peak in the mass spectrum corresponds to an ion with a particular mass-to-charge ratio. The abundance of the two isotopes can be determined from the heights of the peaks.
This video from the Royal Society of Chemistry describes how one type of mass spectrometer works
NASA has flown a different type of mass spectrometer to Mars to search for molecules and life
The arbitrary standard that has been established for describing atomic mass is the atomic mass unit (amu) One-twelfth of the mass of one atom of \( 1\; amu = 1.66 \times 10^{-24}g \), defined as one-twelfth of the mass of one atom of 12C. Because the masses of all other atoms are calculated relative to the 12C standard, 12C is the only atom listed in Table 1.2.2 whose exact atomic mass is equal to the mass number. Experiments have shown that 1 amu = 1.66 × 10−24 g.
Mass spectrometric experiments give a value of 0.167842 for the ratio of the mass of 2H to the mass of 12C, so the absolute mass of 2H is
\(\dfrac{mass\; of\;_{}^{2}\textrm{H}}{mass\; of\;_{}^{12}\textrm{C}} \times mass\; of\; _{}^{12}\textrm{C} = 0.167842\;\times\;12\;amu\;=\;2.104104\;amu\)
The masses of the other elements are determined in a similar way.
The periodic table lists the atomic masses of all the elements. If you compare these values with those given for some of the isotopes in Table 1.2,2, you can see that the atomic masses given in the periodic table never correspond exactly to those of any of the isotopes. Because most elements exist as mixtures of several stable isotopes, the atomic mass of an element is defined as the weighted average of the masses of the isotopes. For example, naturally occurring carbon is largely a mixture of two isotopes: 98.89% 12C (mass = 12 amu by definition) and 1.11% 13C (mass = 13.003355 amu). The percent abundance of 14C is so low that it can be ignored in this calculation. The average atomic mass of carbon is then calculated as
(0.9889 × 12 amu) + (0.0111 × 13.003355 amu) = 12.01 amu
Carbon is predominantly 12C, so its average atomic mass should be close to 12 amu, which is in agreement with our calculation.
The value of 12.01 is shown under the symbol for C in the periodic table although without the abbreviation amu, which is customarily omitted. Thus the tabulated atomic mass of carbon or any other element is the weighted average of the masses of the naturally occurring isotopes.
Example 1.2.2
Naturally occurring bromine consists of the two isotopes listed in the following table:
| Isotope | Exact Mass (amu) | Percent Abundance (%) |
|---|---|---|
| 79Br | 78.9183 | 50.69 |
| 81Br | 80.9163 | 49.31 |
Calculate the atomic mass of bromine.
Given: exact mass and percent abundance
Asked for: atomic mass
Strategy:
A Convert the percent abundences to decimal form to obtain the mass fraction of each isotope.
B Multiply the exact mass of each isotope by its corresponding mass fraction (percent abundance ÷ 100) to obtain its weighted mass.
C Add together the weighted masses to obtain the atomic mass of the element.
D Check to make sure that your answer makes sense.
Solution:
A The atomic mass is the weighted average of the masses of the isotopes. In general, we can write
atomic mass of element = [(mass of isotope 1 in amu) (mass fraction of isotope 1)] + [(mass of isotope 2) (mass fraction of isotope 2)] + …Bromine has only two isotopes. Converting the percent abundances to mass fractions gives
79Br: 79.9183 amu × 0.5069 = 40.00 amu
B Multiplying the exact mass of each isotope by the corresponding mass fraction gives the isotope’s weighted mass:
79Br: 79.9183 amu × 0.5069 = 40.00 amu
81Br: 80.9163 amu × 0.4931 = 39.90 amu
C The sum of the weighted masses is the atomic mass of bromine is
40.00 amu + 39.90 amu = 79.90 amu
D This value is about halfway between the masses of the two isotopes, which is expected because the percent abundance of each is approximately 50%.
Exercise
Magnesium has the three isotopes listed in the following table:
| Isotope | Exact Mass (amu) | Percent Abundance (%) |
|---|---|---|
| 24Mg | 23.98504 | 78.70 |
| 25Mg | 24.98584 | 10.13 |
| 26Mg | 25.98259 | 11.17 |
Use these data to calculate the atomic mass of magnesium.
Answer: 24.31 amu
Summary
Each atom of an element contains the same number of protons, which is the atomic number (Z). Neutral atoms have the same number of electrons and protons. Atoms of an element that contain different numbers of neutrons are called isotopes. Each isotope of a given element has the same atomic number but a different mass number (A), which is the sum of the numbers of protons and neutrons. The relative masses of atoms are reported using the atomic mass unit (amu), which is defined as one-twelfth of the mass of one atom of carbon-12, with 6 protons, 6 neutrons, and 6 electrons. The atomic mass of an element is the weighted average of the masses of the naturally occurring isotopes. When one or more electrons are added to or removed from an atom or molecule, a charged particle called an ion is produced, whose charge is indicated by a superscript after the symbol.
Key Takeaway
- The mass of an atom is a weighted average that is largely determined by the number of its protons and neutrons, whereas the number of protons and electrons determines its charge.
Conceptual Problems
-
Complete the following table for the missing elements, symbols, and numbers of electrons.
Element Symbol Number of Electrons molybdenum 19 titanium B 53 Sm helium 14 -
Complete the following table for the missing elements, symbols, and numbers of electrons.
Element Symbol Number of Electrons lanthanum Ir aluminum 80 sodium Si 9 Be -
Is the mass of an ion the same as the mass of its parent atom? Explain your answer.
-
What isotopic standard is used for determining the mass of an atom?
-
Give the symbol \({}_Z^{A}X\) for these elements, all of which exist as a single isotope.
- beryllium
- ruthenium
- phosphorus
- aluminum
- cesium
- praseodymium
- cobalt
- yttrium
- arsenic
-
Give the symbol \({}_Z^{A}X\) for these elements, all of which exist as a single isotope.
- fluorine
- helium
- terbium
- iodine
- gold
- scandium
- sodium
- niobium
- manganese
-
Identify each element, represented by X, that have the given symbols.
- \( _{26}^{55}\textrm{X}\)
- \( _{33}^{74}\textrm{X}\)
- \( _{12}^{24}\textrm{X}\)
- \( _{53}^{127}\textrm{X}\)
- \( _{18}^{40}\textrm{X}\)
- \( _{63}^{152}\textrm{X}\)
- \( _{26}^{55}\textrm{X}\)
Numerical Problems
-
The isotopes 131I and 60Co are commonly used in medicine. Determine the number of neutrons, protons, and electrons in a neutral atom of each.
-
Determine the number of protons, neutrons, and electrons in a neutral atom of each isotope:
- 97Tc
- 113In
- 63Ni
- 55Fe
- 97Tc
-
Both technetium-97 and americium-240 are produced in nuclear reactors. Determine the number of protons, neutrons, and electrons in the neutral atoms of each.
-
The following isotopes are important in archaeological research. How many protons, neutrons, and electrons does a neutral atom of each contain?
- 207Pb
- 16O
- 40K
- 137Cs
- 40Ar
- 207Pb
-
Copper, an excellent conductor of heat, has two isotopes: 63Cu and 65Cu. Use the following information to calculate the average atomic mass of copper:
Isotope Percent Abundance (%) Atomic Mass (amu) 63Cu 69.09 62.9298 65Cu 30.92 64.9278 -
Silicon consists of three isotopes with the following percent abundances:
Isotope Percent Abundance (%) Atomic Mass (amu) 28Si 92.18 27.976926 29Si 4.71 28.976495 30Si 3.12 29.973770 Calculate the average atomic mass of silicon.
-
Complete the following table for neon. The average atomic mass of neon is 20.1797 amu.
Isotope Percent Abundance (%) Atomic Mass (amu) 20Ne 90.92 19.99244 21Ne 0.257 20.99395 22Ne -
Are \( _{28}^{63}\textrm{X}\)and \( _{29}^{62}\textrm{X}\) isotopes of the same element? Explain your answer.
-
Complete the following table:
Isotope Number of Protons Number of Neutrons Number of Electrons 238X 95 238U 75 112 -
Complete the following table:
Isotope Number of Protons Number of Neutrons Number of Electrons 57Fe 40X 20 36S -
Using a mass spectrometer, a scientist determined the percent abundances of the isotopes of sulfur to be 95.27% for 32S, 0.51% for 33S, and 4.22% for 34S. Use the atomic mass of sulfur from the periodic table and the following atomic masses to determine whether these data are accurate, assuming that these are the only isotopes of sulfur: 31.972071 amu for 32S, 32.971459 amu for 33S, and 33.967867 amu for 34S.
-
The percent abundances of two of the three isotopes of oxygen are 99.76% for 16O, and 0.204% for 18O. Use the atomic mass of oxygen given in the periodic table and the following data to determine the mass of 17O: 15.994915 amu for 16O and 17.999160 amu for 18O.
-
Which element has the higher proportion by mass in NaI?
Which element has the higher proportion by mass in KBr?
Contributors
- Anonymous
Modified by Joshua Halpern, Scott Sinex and Scott Johnson
Periodic Table Song from AsapScience on YouTube
Mass spectrometer explanation from the Royal Society of Chemistry on YouTube
NASA Mass Spectrometer Video from NASA on YouTube