2.4: Density and its Applications
- Page ID
- 3552
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The density of an object is one of its most important and easily-measured physical properties. Densities are widely used to identify pure substances and to characterize and estimate the composition of many kinds of mixtures. The purpose of this lesson is to show how densities are defined, measured, and utilized, and to make sure you understand the closely-related concepts of buoyancy and specific gravity, and the roles they play in our lives and the environment.
What is Density?
Most of us have long understood that "oil is lighter than water", or that iron is "heavier" than sugar. But in making such statements, we are implicitly comparing equal volumes of these substances: after all, we know that a cup of sugar will weigh more than a single ordinary steel nail. Mass and volume are measures of the quantity of a substance, and as such are defined as extensive properties of matter. The ratio of two extensive properties is always an intensive property — one that characterizes a particular kind of matter, independently of its size or mass. It is this ratio, (mass ÷ volume), that we are concerned with in this Module.
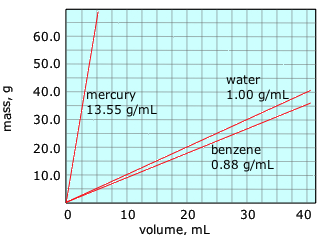
These plots show how the masses of three liquids vary with their volumes. Notice that
- the plots all have the same origin of (0,0): if the mass is zero, so is the volume;
- the plots are all straight lines, which signify direct proportionality.
The only difference between these plots is their slopes. Denoting mass and volume by \(m\) and \(V\) respectively, we can write the equation of each line as \(m = \rho V\), where the slope \(\rho\) (Greek lower-case rho) is the proportionality constant that relates mass to volume. This quantity \(\rho\) is known as the density, which is usually defined as the mass per unit volume:
\[\rho = \dfrac{m}{V}.\]
The volume units milliliter (mL) and cubic centimeter (cm3) are identical and are commonly used interchangeably.
The general meaning of density is the amount of anything per unit volume. What we conventionally call the "density" is more precisely known as the "mass density".
Density can be expressed in any combination of mass and volume units; the most commonly seen units are grams per mL (g mL–1, g cm–3), or kilograms per liter.
1 kg m–3 = 10–3 g L–1 = 62.4 lb ft–3
Densities of Common Substances
The range of densities encountered in the world spans a remarkably wide range, from essentially zero in outer space to the unimaginably huge values found in stellar bodies. These very high densities represent the ultimate limits of how much mass can be packed into a given volume. The following chart will give you some feeling for the values of density found in nature generally (top), in common solids (middle), and in gases and liquids (bottom). Please note that in order to depict reasonably wide ranges of values in limited space, the density scales are logarithmic; thus zero on these scales corresponds to the density of water (100 = 1 g cm–3). Densities listed for ordinary substances (including gases) are mostly those at around 20° C.

Solids, liquids and gases
In general, gases have the lowest densities, but these densities are highly dependent on the pressure and temperature which must always be specified. To the extent that a gas exhibits ideal behavior (low pressure, high temperature), the density of a gas is directly proportional to the masses of its component atoms, and thus to its molecular weight. Measurement of the density of a gas is a simple experimental way of estimating its molecular weight.

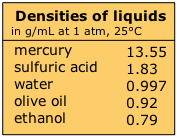
Liquids encompass an intermediate range of densities. Mercury, being a liquid metal, is something of an outlier. Liquid densities are largely independent of pressure, but they are somewhat temperature-sensitive.
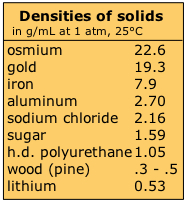
The density range of solids is quite wide. Metals, whose atoms pack together quite compactly, have the highest densities, although that of lithium, the highest metallic element, is quite low. Composite materials such as wood and high-density polyurethane foam contain void spaces which reduce the average density.
How the temperature affects density
All substances tend to expand as they are heated, causing the same mass to occupy a greater volume, and thus lowering the density. For most solids, this expansion is relatively small, but it is far from negligible; for liquids, it is greater. The volumes of gases, as you may already know, are highly temperature-sensitive, and so, of course, are their densities.
What is the cause of thermal expansion? As molecules acquire thermal energy, they move about more vigorously. In condensed phases (liquids and solids), this motion has the character of an irregular kind of bumping or jostling that causes the average distances between the molecules to increase, thus leading to increased volume and smaller density.
Applications of density
Lava Lamps
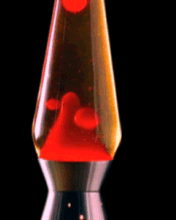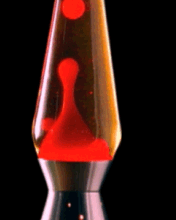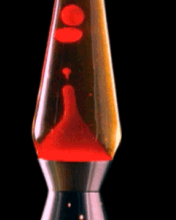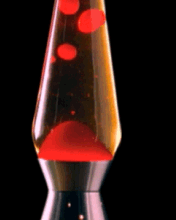
Known more generically as "fluid motion lamps", these devices became popular in the 1970's and provide a nice, if somewhat mesmerizing illustration of density and buoyancy in action as the blobs of oozing goo move up and down in ever-changing shapes. These lamps consist of a container of water in which is placed a colored organic oily liquid that does not mix with water, thus constituting a second phase. The composition of the oil phase is such that its density is slightly greater than that of water at room temperature, so it normally resides at the bottom of the container. When the lamp is turned on, a heat source (usually an incandescent light bulb) concealed in the base of the container heats the oil phase. This reduces its density to a value below that of the water, causing blobs of oil to rise to the top of the container. Being now far removed from the heat source, the blobs cool down and sink back to the bottom, where they repeat the cycle.
Contributors and Attributions
Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook


