1.7: de Broglie Waves can be Experimentally Observed
- Page ID
- 210781
- To present the experimental evidence behind the wave-particle duality of matter
The validity of de Broglie’s proposal was confirmed by electron diffraction experiments of G.P. Thomson in 1926 and of C. Davisson and L. H. Germer in 1927. In these experiments it was found that electrons were scattered from atoms in a crystal and that these scattered electrons produced an interference pattern. The interference pattern was just like that produced when water waves pass through two holes in a barrier to generate separate wave fronts that combine and interfere with each other. These diffraction patterns are characteristic of wave-like behavior and are exhibited by both matter (e.g., electrons and neutrons) and electromagnetic radiation. Diffraction patterns are obtained if the wavelength is comparable to the spacing between scattering centers.
Diffraction occurs when waves encounter obstacles whose size is comparable with its wavelength.
Continuing with our analysis of experiments that lead to the new quantum theory, we now look at the phenomenon of electron diffraction.
Light Diffraction (Young's Double Slit Experiment)
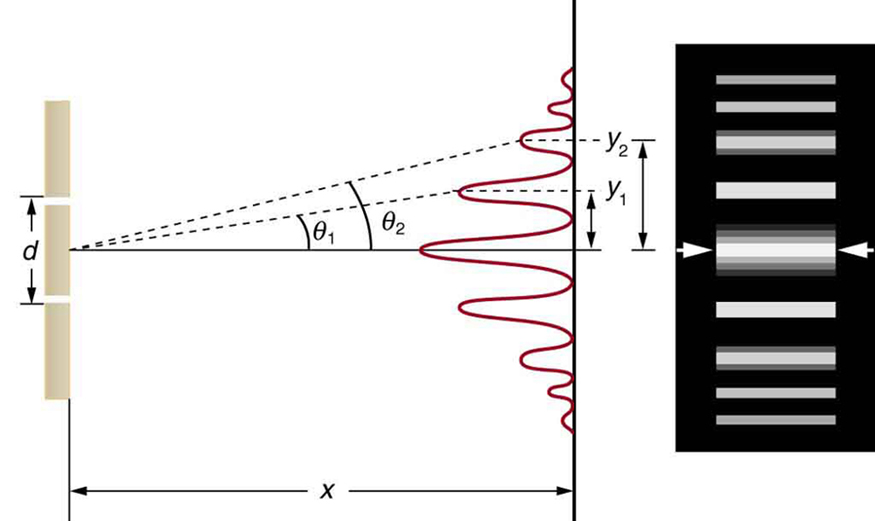
It is well-known that light has the ability to diffract around objects in its path, leading to an interference pattern that is particular to the object. This is, in fact, how holography works (the interference pattern is created by allowing the diffracted light to interfere with the original beam so that the hologram can be viewed by shining the original beam on the image). A simple illustration of light diffraction is the Young double slit experiment (Figure \(\PageIndex{1}\)).
Interference is a wave phenomenon in which two waves superimpose to form a resultant wave of greater or lower amplitude. It is the primary property used to identify wave behavior.
Here, we use water waves (pictured as waves in a plane parallel to the double slit apparatus) and observe what happens when they impinge on the slits. Each slit then becomes a point source for spherical waves that subsequently interfere with each other, giving rise to the light and dark fringes on the screen at the right (Figure \(\PageIndex{2}\)).
Electron Diffraction (Davisson–Germer Experiment)
According to classical physics, electrons should behave like particles - they travel in straight lines and do not curve in flight unless acted on by an external agent, like a magnetic field. In this model, if we fire a beam of electrons through a double slit onto a detector, we should get two bands of "hits", much as you would get if you fired a machine gun at the side of a house with two windows - you would get two areas of bullet-marked wall inside, and the rest would be intact Figure \(\PageIndex{3}\) (left).
However, if the slits are made small enough and close enough together, we actually observe the electrons are diffracting through the slits and interfering with each other just like waves. This means that the electrons have wave-particle duality, just like photons, in agreement with de Broglie's hypothesis discussed previously. In this case, they must have properties like wavelength and frequency. We can deduce the properties from the behavior of the electrons as they pass through our diffraction grating.
This was a pivotal result in the development of quantum mechanics. Just as the photoelectric effect demonstrated the particle nature of light, the Davisson–Germer experiment showed the wave-nature of matter, and completed the theory of wave-particle duality. For physicists this idea was important because it meant that not only could any particle exhibit wave characteristics, but that one could use wave equations to describe phenomena in matter if one used the de Broglie wavelength.
An electron, indeed any particle, is neither a particle nor a wave. Describing the electron as a particle is a mathematical model that works well in some circumstances while describing it as a wave is a different mathematical model that works well in other circumstances. When you choose to do some calculation of the electron's behavior that treats it either as a particle or as a wave, you're not saying the electron is a particle or is a wave: you're just choosing the mathematical model that makes it easiest to do the calculation.
Neutron Diffraction
Like all quantum particles, neutrons can also exhibit wave phenomena and if that wavelength is short enough, atoms or their nuclei can serve as diffraction obstacles. When a beam of neutrons emanating from a reactor is slowed down and selected properly by their speed, their wavelength lies near one angstrom (0.1 nanometer), the typical separation between atoms in a solid material. Such a beam can then be used to perform a diffraction experiment. Neutrons interact directly with the nucleus of the atom, and the contribution to the diffracted intensity depends on each isotope; for example, regular hydrogen and deuterium contribute differently. It is also often the case that light (low Z) atoms contribute strongly to the diffracted intensity even in the presence of large Z atoms.
Neutrons have no electric charge, so they do not interact with the atomic electrons. Hence, they are very penetrating (e.g., typically 10 cm in lead). Neutron diffraction was proposed in 1934, to exploit de Broglie’s hypothesis about the wave nature of matter. Calculate the momentum and kinetic energy of a neutron whose wavelength is comparable to atomic spacing (\(1.8 \times 10^{-10}\, m\)).
Solution
This is a simple use of de Broglie’s equation
\[\lambda = \dfrac{h}{p} \nonumber\]
where we recognize that the wavelength of the neutron must be comparable to atomic spacing (let's assumed equal for convenience, so \(\lambda = 1.8 \times 10^{-10}\, m\)). Rearranging the de Broglie wavelength relationship above to solve for momentum (\(p\)):
\[\begin{align} p &= \dfrac{h}{\lambda} \nonumber \\[4pt] &= \dfrac{6.6 \times 10^{-34} J s}{1.8 \times 10^{-10} m} \nonumber \\[4pt] &= 3.7 \times 10^{-24}\, kg \,\,m\, \,s^{-1} \nonumber \end{align} \nonumber\]
The relationship for kinetic energy is
\[KE = \dfrac{1}{2} mv^2 = \dfrac{p^2}{2m} \nonumber\]
where \(v\) is the velocity of the particle. From the reference table of physical constants, the mass of a neutron is \(1.6749273 \times 10^{−27}\, kg\), so
\[\begin{align*} KE &= \dfrac{(3.7 \times 10^{-24}\, kg \,\,m\, \,s^{-1} )^2}{2 (1.6749273 \times 10^{−27}\, kg)} \\ &=4.0 \times 10^{-21} J \end{align*}\]
The neutrons released in nuclear fission are ‘fast’ neutrons, i.e. much more energetic than this. Their wavelengths be much smaller than atomic dimensions and will not be useful for neutron diffraction. We slow down these fast neutrons by introducing a "moderator", which is a material (e.g., graphite) that neutrons can penetrate, but will slow down appreciable.
Contributors
Michael Fowler (Beams Professor, Department of Physics, University of Virginia)
- Wikipedia
- John Rennie (StackExchange)