1.2: Quantum Hypothesis Used for Blackbody Radiation Law
- Page ID
- 210776
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To understand how energy is quantized in blackbody radiation
By the late 19th century, many physicists thought their discipline was well on the way to explaining most natural phenomena. They could calculate the motions of material objects using Newton’s laws of classical mechanics, and they could describe the properties of radiant energy using mathematical relationships known as Maxwell’s equations, developed in 1873 by James Clerk Maxwell, a Scottish physicist. The universe appeared to be a simple and orderly place, containing matter, which consisted of particles that had mass and whose location and motion could be accurately described, and electromagnetic radiation, which was viewed as having no mass and whose exact position in space could not be fixed. Thus matter and energy were considered distinct and unrelated phenomena. Soon, however, scientists began to look more closely at a few inconvenient phenomena that could not be explained by the theories available at the time.
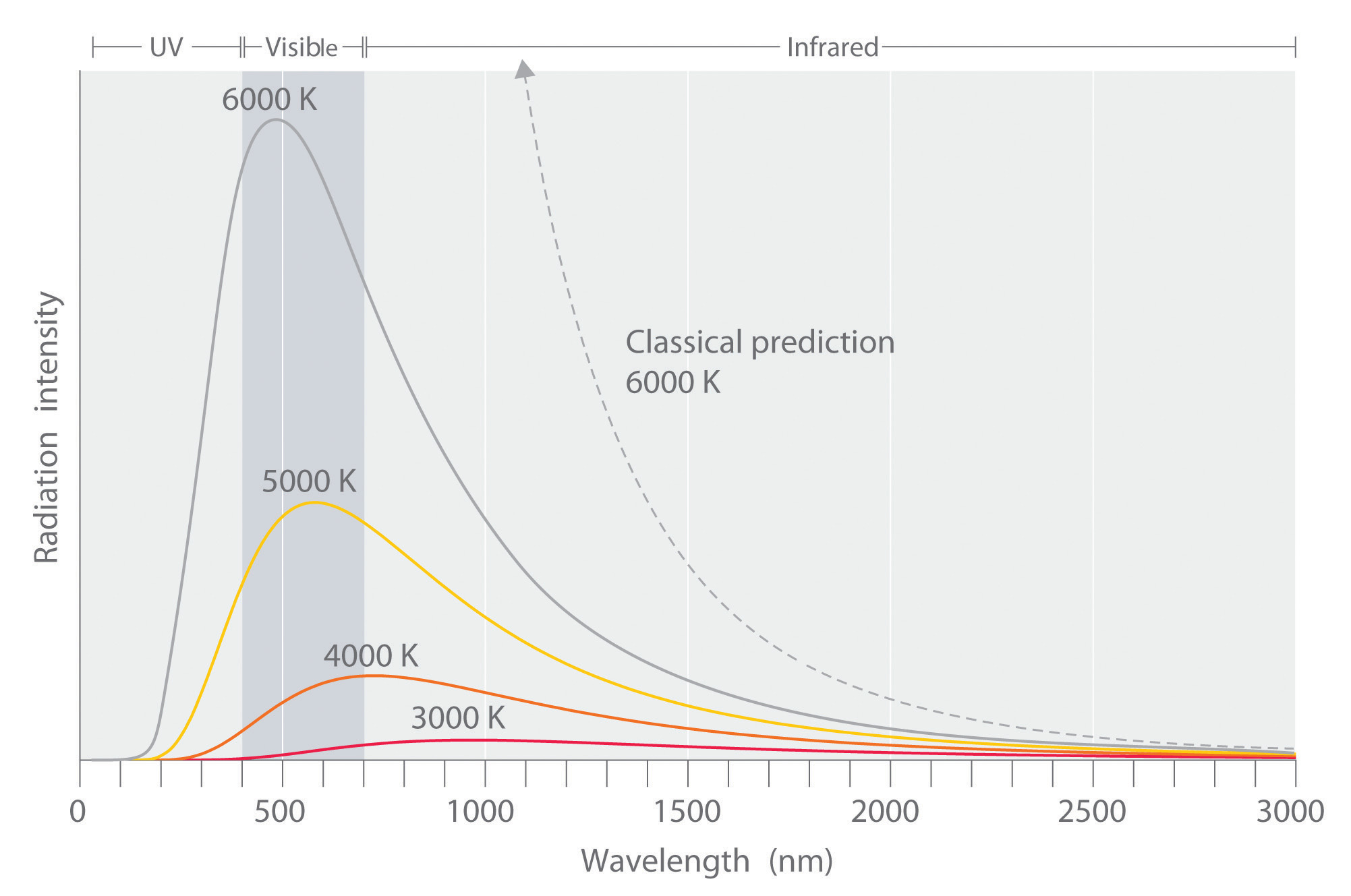
One experimental phenomenon that could not be adequately explained by classical physics was blackbody radiation. Attempts to explain or calculate this spectral distribution from classical theory were complete failures. A theory developed by Rayleigh and Jeans predicted that the intensity should go to infinity at short wavelengths. Since the intensity actually drops to zero at short wavelengths, the Rayleigh-Jeans result was called the “ultraviolet catastrophe.” There was no agreement between theory and experiment in the ultraviolet region of the blackbody spectrum.
Quantizing Electrons in the Radiator
In 1900, the German physicist Max Planck (1858–1947) explained the ultraviolet catastrophe by proposing that the energy of electromagnetic waves is quantized rather than continuous. This means that for each temperature, there is a maximum intensity of radiation that is emitted in a blackbody object, corresponding to the peaks in Figure \(\PageIndex{1}\), so the intensity does not follow a smooth curve as the temperature increases, as predicted by classical physics. Thus energy could be gained or lost only in integral multiples of some smallest unit of energy, a quantum (the smallest possible unit of energy). Energy can be gained or lost only in integral multiples of a quantum.
Although quantization may seem to be an unfamiliar concept, we encounter it frequently. For example, US money is integral multiples of pennies. Similarly, musical instruments like a piano or a trumpet can produce only certain musical notes, such as C or F sharp. Because these instruments cannot produce a continuous range of frequencies, their frequencies are quantized. Even electrical charge is quantized: an ion may have a charge of −1 or −2, but not −1.33 electron charges.
Planck's quantization of energy is described by the his famous equation:
\[ E=h \nu \label{Eq1.2.1}\]
where the proportionality constant \(h\) is called Planck’s constant, one of the most accurately known fundamental constants in science
\[h=6.626070040(81) \times 10^{−34}\, J\cdot s\]
However, for our purposes, its value to four significant figures is sufficient:
\[h = 6.626 \times 10^{−34} \,J\cdot s\]
As the frequency of electromagnetic radiation increases, the magnitude of the associated quantum of radiant energy increases. By assuming that energy can be emitted by an object only in integral multiples of hν, Planck devised an equation that fit the experimental data shown in Figure \(\PageIndex{2}\). We can understand Planck’s explanation of the ultraviolet catastrophe qualitatively as follows: At low temperatures, radiation with only relatively low frequencies is emitted, corresponding to low-energy quanta. As the temperature of an object increases, there is an increased probability of emitting radiation with higher frequencies, corresponding to higher-energy quanta. At any temperature, however, it is simply more probable for an object to lose energy by emitting a large number of lower-energy quanta than a single very high-energy quantum that corresponds to ultraviolet radiation. The result is a maximum in the plot of intensity of emitted radiation versus wavelength, as shown in Figure \(\PageIndex{2}\), and a shift in the position of the maximum to lower wavelength (higher frequency) with increasing temperature.
At the time he proposed his radical hypothesis, Planck could not explain why energies should be quantized. Initially, his hypothesis explained only one set of experimental data—blackbody radiation. If quantization were observed for a large number of different phenomena, then quantization would become a law. In time, a theory might be developed to explain that law. As things turned out, Planck’s hypothesis was the seed from which modern physics grew.
Max Planck explain the spectral distribution of blackbody radiation as result from oscillations of electrons. Similarly, oscillations of electrons in an antenna produce radio waves. Max Planck concentrated on modeling the oscillating charges that must exist in the oven walls, radiating heat inwards and—in thermodynamic equilibrium—themselves being driven by the radiation field. He found he could account for the observed curve if he required these oscillators not to radiate energy continuously, as the classical theory would demand, but they could only lose or gain energy in chunks, called quanta, of size \(h\nu\), for an oscillator of frequency \(\nu\) (Equation \(\ref{Eq1.2.1} \)).
With that assumption, Planck calculated the following formula for the radiation energy density inside the oven:
\[ \begin{align} d\rho(\nu,T) &= \rho_\nu (T) d\nu \\[4pt] &= \dfrac {2 h \nu^3}{c^2} \cdot \dfrac {1 }{\exp \left( \dfrac {h\nu}{k_B T}\right)-1} d\nu \label{Eq2a} \end{align}\]
with
- \(\pi = 3.14159\)
- \(h\) = \(6.626 \times 10^{-34} J\cdot s\)
- \(c\) = \(3.00 \times 10^{8}\, \dfrac{m}{s}\)
- \(\nu\) = \(\frac {1}{s}\)
- \(k_B\) = \(1.38 \times 10^{-23} \,\dfrac {J}{K}\)
- \(T\) is absolute temperature (in Kelvin)
Planck's radiation energy density (Equation \(\ref{Eq2a}\)) can also be expressed in terms of wavelength \(\lambda\).
\[\rho (\lambda, T) d \lambda = \dfrac {2 hc^2}{\lambda ^5} \dfrac {1}{ \exp \left(\dfrac {hc}{\lambda k_B T} \right) - 1} d \lambda \label{Eq2b}\]
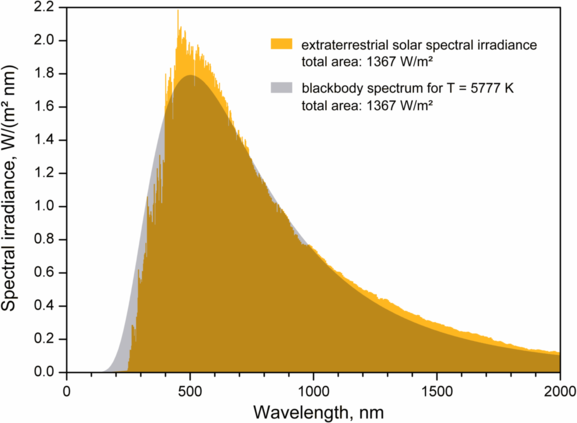
Planck's equation (Equation \(\ref{Eq2b}\)) gave an excellent agreement with the experimental observations for all temperatures.
In addition to being a physicist, Planck was a gifted pianist, who at one time considered music as a career. During the 1930s, Planck felt it was his duty to remain in Germany, despite his open opposition to the policies of the Nazi government.

One of his sons was executed in 1944 for his part in an unsuccessful attempt to assassinate Hitler and bombing during the last weeks of World War II destroyed Planck’s home. After WWII, the major German scientific research organization was renamed the Max Planck Society.
Use Equation \(\ref{Eq2b}\) to show that the units of \(ρ(λ,T)\,dλ\) are \(J/m^3\) as expected for an energy density.
The near perfect agreement of this formula with precise experiments (e.g., Figure \(\PageIndex{3}\)), and the consequent necessity of energy quantization, was the most important advance in physics in the century. His blackbody curve was completely accepted as the correct one: more and more accurate experiments confirmed it time and again, yet the radical nature of the quantum assumption did not sink in. Planck was not too upset—he didn’t believe it either, he saw it as a technical fix that (he hoped) would eventually prove unnecessary.
Part of the problem was that Planck’s route to the formula was long, difficult and implausible—he even made contradictory assumptions at different stages, as Einstein pointed out later. However, the result was correct anyway!
The mathematics implied that the energy given off by a blackbody was not continuous, but given off at certain specific wavelengths, in regular increments. If Planck assumed that the energy of blackbody radiation was in the form
\[E = nh \nu\]
where \(n\) is an integer (now called a quantum number), then he could explain what the mathematics represented. This was indeed difficult for Planck to accept, because at the time, there was no reason to presume that the energy should only be radiated at specific frequencies. Nothing in Maxwell’s laws suggested such a thing. It was as if the vibrations of a mass on the end of a spring could only occur at specific energies. Imagine the mass slowly coming to rest due to friction, but not in a continuous manner. Instead, the mass jumps from one fixed quantity of energy to another without passing through the intermediate energies.
To use a different analogy, it is as if what we had always imagined as smooth inclined planes were, in fact, a series of closely spaced steps that only presented the illusion of continuity.
Summary
The agreement between Planck’s theory and the experimental observation provided strong evidence that the energy of electron motion in matter is quantized. In the next two sections, we will see that the energy carried by light also is quantized in units of h \(\bar {\nu}\). These packets of energy are called “photons.”
Contributors
Michael Fowler (Beams Professor, Department of Physics, University of Virginia)
David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski ("Quantum States of Atoms and Molecules")
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).

