8.8: Isotope Effects in Chemical Reactions

The kinetic isotope effect (KIE) is a phenomenon associated with isotopically substituted molecules exhibiting different reaction rates. Isotope effects such as KIEs are invaluable tools in both physical and biological sciences and are used to aid in the understanding of reaction kinetics, mechanisms, and solvent effects.

Introduction

Research was first introduced on this topic over 50 years ago and has grown into an enormous field. The scientists behind much of the understanding and development of kinetic isotope effects were Jacob Bigeleisen and Maria Goeppert Mayer who published the first paper on isotope effects [J. Chem. Phys., 15, 261 (1947)]. Kinetic isotope effects specifically explore the change in rate of a reaction due to isotopic substitution.

An element is identified by its symbol, mass number, and atomic number. The atomic number is the number of protons in the nucleus while the mass number is the total number of protons and neutrons in the nucleus. Isotopes are two atoms of the same element that have the same number of protons but different numbers of neutrons. Isotopes are specified by the mass number.

As an example consider the two isotopes of chlorine, you can see that their mass numbers vary, with ³⁵Cl being the most abundant isotope, while their atomic numbers remain the same at 17.

\[ ^{35}Cl \;\text{and}\; ^{37}Cl\]

The most common isotope used in light atom isotope effects is hydrogen (\(^{1}H\)) commonly replaced by its isotope deuterium (\(^{2}H\)). Note: Hydrogen also has a third isotope, tritium (\(^{2}H\)). Isotopes commonly used in heavy atom isotope effects include carbon (\(^{12}C\), \(^{13}C\), nitrogen (\(^{14}N\), \(^{15}N\)), oxygen, sulfur, and bromine. Not all elements exhibit reasonably stable isotopes (i.e. Fluorine, \(^{19}F\)), but those that due serve as powerful tools in isotope effects.

Potential Energy Surfaces

Understanding potential energy surfaces is important in order to be able to understand why and how isotope effects occur as they do. The harmonic oscillator approximation is used to explain the vibrations of a diatomic molecule. The energies resulting from the quantum mechanic solution for the harmonic oscillator help to define the internuclear potential energy of a diatomic molecule and are

\[ E_n = \left(n + \dfrac{1}{2}\right)h \nu \label{1}\]

where

• n is a positive integer (n=1,2,3...),
• h is Planck's constant and
• \(\nu\) is the frequency of vibration.

The Morse potential is an analytic expression that is used as an approximation to the intermolecular potential energy curves:

\[ V(l) = D_e{\left(1-e^{-\beta(l-l_o)}\right)}^2 \label{2}\]

where

• \(V(l)\) is the potential energy,
• \(D_e\) is the dissociation energy of the molecule,
• \( \beta \) is the measure of the curvature of the potential at its minimum,
• \(l\) is displacement, and
• \(l_o\) is the equilibrium bond length.

The \(D_e\), \( \beta \), and \(l_o\) variables can be looked up in a textbook or CRC handbook.

Below is an example of a Morse potential curve with the zero point vibrational energies of two isotopic molecules (for example R-H and R-D where R is a group/atom that is much heavier than H or D). The y-axis is potential energy and the x axis is internuclear distance. In this figure E_D^o and E_H^o correspond to the zero point energies of deuterium and hydrogen. The zero point energy is the lowest possible energy of a system and equates to the ground state energy. Zero point energy is dependent upon the reduced mass of the molecule as will be shown in the next section. The heavier the molecule or atom, the lower the frequency of vibration and the smaller the zero point energy. Lighter molecules or atoms have a greater frequency of vibration and a higher zero point energy. We see this is the figure below where deuterium is heavier than hydrogen and therefore has the lower zero point energy.

This results in different bond dissociation energies for R-D and R-H. The bond dissociation energy for R-D (E_D) is greater than the bond dissociation energy of R-H (E_H). This difference in energy due to isotopic replacement results in differing rates of reaction, the effect that is measured in kinetic isotope effects. The reaction rate for the conversion of R-D is slower than the reaction rate for the conversion of R-H.

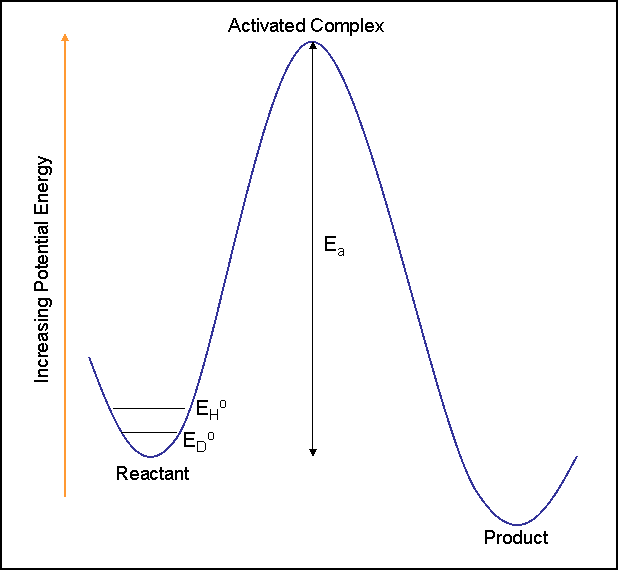
It is important to note that isotope replacement does not change the electronic structure of the molecule or the potential energy surfaces of the reactions the molecule may undergo. Only the rate of the reaction is affected.

Activation Energies

The energy of the vibrational levels of a vibration (i.e., a bond) in a molecule is given by

\[ E_n = \left(n + \dfrac{1}{2}\right)h \nu \label{3} \]

where we assume that the molecule is in its ground state and we can compare zero-point vibrational energies,

\[ E_o = \left(\dfrac{1}{2}\right)hv \label{4}\]

Using the harmonic oscillator approximation the fundamental vibrational frequency is

\[ \nu = \dfrac{1}{2 \pi} \sqrt{ \dfrac {k}{\mu} } \label{5}\]

where

• \(k\) is the force constant of the bond and
• \( \mu \) is the reduced mass

\[ \mu = \dfrac{m_1m_2}{m_1+m_2} \label{6}\]

The Arrhenius equation is used to determine reaction rates and activation energies and since we are interested in the change in rate of reactions with different isotopes, this equation is very important,

\[ k = Ae^{-\frac{E_a}{kT}} \label{7} \]

where

• \(k\) is the reaction rate,
• \(E_a\) is the activation energy, and
• \(A\) is the Arrhenius constant.

The Arrhenius equation can be used to compare the rates of a reaction with R-H and R-D,

\[ k_H = A_He^{-\frac{E_a^H}{kT}} \label{8}\]

\[ k_D = A_De^{-\frac{E_a^D}{kT}} \label{9} \]

where k_H and k_D are the rates of reaction associated with R-H and the isotope substituted R-D. We will then assume the Arrhenius constants are equal (\(A_H=A_D\)). The ratio of the rates of reaction gives an approximation for the isotope effect resulting in:

\[ \dfrac{k_H}{k_D} = e^{-\frac{E_a^H - E_a^D}{kT}} \label{10}\]

By using the relationship that for both R-H and R-D

\[ E_o = \left(\dfrac{1}{2}\right)h\nu \label{11} \]

a substitution can be made resulting in

\[\dfrac{k_H}{k_D} = e^{\frac{h(\nu_H - \nu_D)}{2kT}} \label{12}\]

The vibrational frequency (Equation 5) can then be substituted for R-H and R-D and the value of the expected isotope effect can be calculated.

\[\dfrac{k_H}{k_D} = e^{\dfrac {h \left( \dfrac{k_{RH}}{\mu_{RH}} - \dfrac{k_{RD}}{\mu_{RD}} \right)}{4\pi kT}} \label{13}\]

The same general procedure can be followed for any isotope substitution.

In summary, the greater the mass the more energy is needed to break bonds. A heavier isotope forms a stronger bond. The resulting molecule has less of a tendency to dissociate. The increase in energy needed to break the bond results in a slower reaction rate and the observed isotope effect.

Kinetic Isotope Effects

Kinetic Isotope Effects (KIEs) are used to determine reaction mechanisms by determining rate limiting steps and transition states and are commonly measured using NMR to detect isotope location or GC/MS to detect mass changes. In a KIE experiment an atom is replaced by its isotope and the change in rate of the reaction is observed. A very common isotope substitution is when hydrogen is replaced by deuterium. This is known as a deuterium effect and is expressed by the ratio k_H/k_D (as explained above). Normal KIEs for the deuterium effect are around 1 to 7 or 8. Large effects are seen because the percentage mass change between hydrogen and deuterium is great. Heavy atom isotope effects involve the substitution of carbon, oxygen, nitrogen, sulfur, and bromine, with effects that are much smaller and are usually between 1.02 and 1.10. The difference in KIE magnitude is directly related to the percentage change in mass. Large effects are seen when hydrogen is replaced with deuterium because the percentage mass change is very large (mass is being doubled) while smaller percent mass changes are present when an atom like sulfur is replaced with its isotope (increased by two mass units).

Primary KIEs

Primary kinetic isotope effects are rate changes due to isotopic substitution at a site of bond breaking in the rate determining step of a reaction.

Example

Consider the bromination of acetone: kinetic studies have been performed that show the rate of this reaction is independent of the concentration of bromine. To determine the rate determining step and mechanism of this reaction the substitution of a deuterium for a hydrogen can be made.

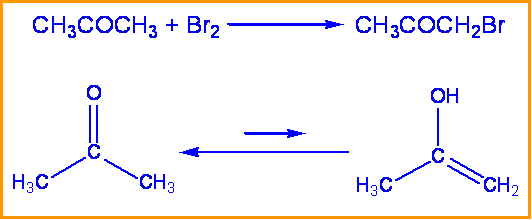
When hydrogen was replaced with deuterium in this reaction a \(k_H \over k_D \) of 7 was found. Therefore the rate determining step is the tautomerization of acetone and involves the breaking of a C-H bond. Since the breaking of a C-H bond is involved, a substantial isotope effect is expected.

Heavy Atom Isotope Effects

A rule of thumb for heavy atom isotope effects is that the maximum isotopic rate ratio is proportional to the square root of the inverse ratio of isotopic masses.

• Expected: \[\dfrac{k_{32}}{k_{34}} = \sqrt{\dfrac{34}{32}}=1.031\]
• Experimental: \[\dfrac{k_{32}}{k_{34}} = 1.072\]

Secondary KIEs

Secondary kinetic isotope effects are rate changes due to isotopic substitutions at a site other than the bond breaking site in the rate determining step of the reaction. These come in three forms: \(\alpha\), \(\beta\), and \(\gamma\) effects.

\(\beta\) secondary isotope effects occur when the isotope is substituted at a position next to the bond being broken.

\[\ce{(CH3)2CHBr + H2O ->[k_H] (CH3)2CHOH}\]

\[\ce{(CD3)2CHBr + H2O ->[k_D] (CD3)2CHOH}\]

This is thought to be due to hyperconjugation in the transition state. Hyperconjugation involves a transfer of electron density from a sigma bond to an empty p orbital (for more on hyperconjugation see outside links).

Solvent Effects in Reactions

Reactions may be affected by the type of solvent used (for example H₂O to D₂O or ROH to ROD). There are three main ways solvents effect reactions:

1. The solvent can act as a reactant resulting in a primary isotope effect.
2. Rapid hydrogen exchange can occur between substrate molecules labeled with deuterium and hydrogen atoms in the solvent. Deuterium may change positions in the molecule resulting in a new molecule that is then reacted in the rate determining step of the reaction.
3. The nature of solvent and solute interactions may also change with differing solvents. This could change the energy of the transition state and result in a secondary isotope effects.

References

1. Baldwin, J.E., Gallagher, S.S., Leber, P.A., Raghavan, A.S., Shukla, R.; J. Org. Chem. 2004, 69, 7212-7219 (This is a great paper using kinetic isotope effects to determine a reaction mechanism. It will interest the organic chemistry oriented reader.)
2. Bigeleisen, J., Goeppert, M., J. Chem. Phys. 1947, 15, 261.
3. Chang, R.; Physical Chemistry for the Chemical and Biological Sciences; University Science Books: Sausalito, CA, 2000, pp 480-483.
4. Isaacs, N.; Physical Organic Chemistry; John Wiley & Sons Inc.: New York, NY; 1995, 2nd ed, pp 287-313.
5. March, J., Smith, M.B.; March’s Advanced Organic Chemistry; John Wiley & Sons, Inc.: Hoboken, NJ, 2007; 6th ed.
6. McMurry, J.; Organic Chemistry; Brooks & Cole: Belmont, CA; 2004, 6th ed.
7. McQuarrie, D.; Quantum Chemistry; University Science Books: Sausalito, CA, 2008, 2nd ed.
8. Rouhi, A.; C&EN. 1997, 38-42.

Problems

1. Describe the difference between primary and secondary kinetic isotope effects.
2. Estimate the k_N-H/k_N-D for a deuterium substitution on nitrogen given that v_H=9.3x1013 Hz and the activation energy is equal to 5.31 kJ/mol.
3. Using the 'rule of thumb' for heavy isotope effects, calculate the expected effect for a bromine isotope substitution, ⁷⁹Br and ⁸¹Br.
4. Explain some of the main ways kinetic isotope effects are used.
5. As discussed, the rate-limiting step in the bromination of acetone is the breaking of a carbon-hydrogen bond. Estimate kC-H/KC-D for this reaction at 285 K. (Given: vtilde_C-H=3000 cm^-1 and vtilde_C-D=2100 cm^-1)

Solutions

1. Primary isotope effects involve isotopic substitution at the bond being broken in a reaction, while secondary isotope effects involve isotopic Substitution on bonds adjacent to the bond being broken.
2. 8.5
3. 1.0126
4. To determine reaction mechanisms, to determine rate limiting steps in reactions, to determine transition states in reactions.
5. 9.685