6.7: Titrations - Lab 8

Last updated
Save as PDF

Page ID: 188853

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Skills to Develop

Accurately perform a titration to calculate the unknown concentration of a solution in a neutralization reaction.
Perform stoichiometric calculations using typical titration data.

In the 18th century, the strength (actually the concentration) of vinegar samples was determined by noting the amount of potassium carbonate, K₂CO₃, which had to be added, a little at a time, before bubbling ceased. The greater the weight of potassium carbonate added to reach the point where the bubbling ended, the more concentrated the vinegar.

We now know that the effervescence that occurred during this process was due to reaction with acetic acid, CH₃CO₂H, the compound primarily responsible for the odor and taste of vinegar. Acetic acid reacts with potassium carbonate according to the following equation:

\[\ce{2CH3CO2H}(aq)+\ce{K2CO3}(s)\rightarrow 2 \ce{KCH3CO3}(aq)+\ce{CO2}(g)+\ce{H2O}(l)\]

The bubbling was due to the production of CO₂.

The test of vinegar with potassium carbonate is one type of quantitative analysis—the determination of the amount or concentration of a substance in a sample. In the analysis of vinegar, the concentration of the solute (acetic acid) was determined from the amount of reactant that combined with the solute present in a known volume of the solution. In other types of chemical analyses, the amount of a substance present in a sample is determined by measuring the amount of product that results.

Titration

The described approach to measuring vinegar strength was an early version of the analytical technique known as titration analysis. A typical titration analysis involves the use of a buret (Figure \(\PageIndex{1}\)) to make incremental additions of a solution containing a known concentration of some substance (the titrant) to a sample solution containing the substance whose concentration is to be measured (the analyte). The titrant and analyte undergo a chemical reaction of known stoichiometry, and so measuring the volume of titrant solution required for complete reaction with the analyte (the equivalence point of the titration) allows calculation of the analyte concentration. The equivalence point of a titration may be detected visually if a distinct change in the appearance of the sample solution accompanies the completion of the reaction. The halt of bubble formation in the classic vinegar analysis is one such example, though, more commonly, special dyes called indicators are added to the sample solutions to impart a change in color at or very near the equivalence point of the titration. Equivalence points may also be detected by measuring some solution property that changes in a predictable way during the course of the titration. Regardless of the approach taken to detect a titration’s equivalence point, the volume of titrant actually measured is called the end point. Properly designed titration methods typically ensure that the difference between the equivalence and end points is negligible. Though any type of chemical reaction may serve as the basis for a titration analysis, the three described in this chapter (precipitation, acid-base, and redox) are most common. Additional details regarding titration analysis are provided in the chapter on acid-base equilibria.

Two pictures are shown. In a, a person is shown pouring a liquid from a small beaker into a buret. The person is wearing goggles and gloves as she transfers the solution into the buret. In b, a close up view of the markings on the side of the buret is shown. The markings for 10, 15, and 20 are clearly shown with horizontal rings printed on the buret. Between each of these whole number markings, half markings are also clearly shown with horizontal line segment markings. — Figure \(\PageIndex{1}\): (a) A student fills a buret in preparation for a titration analysis. (b) A typical buret permits volume measurements to the nearest 0.1 mL. (credit a: modification of work by Mark Blaser and Matt Evans; credit b: modification of work by Mark Blaser and Matt Evans)

Example \(\PageIndex{1}\): Titration Analysis

The end point in a titration of a 50.00-mL sample of aqueous HCl was reached by addition of 35.23 mL of 0.250 M NaOH titrant. The titration reaction is:

\[\ce{HCl}(aq)+\ce{NaOH}(aq)\rightarrow \ce{NaCl}(aq)+\ce{H2O}(l)\]

What is the molarity of the HCl?

Solution

As for all reaction stoichiometry calculations, the key issue is the relation between the molar amounts of the chemical species of interest as depicted in the balanced chemical equation. The approach outlined in previous modules of this chapter is followed, with additional considerations required, since the amounts of reactants provided and requested are expressed as solution concentrations.

For this exercise, the calculation will follow the following outlined steps:

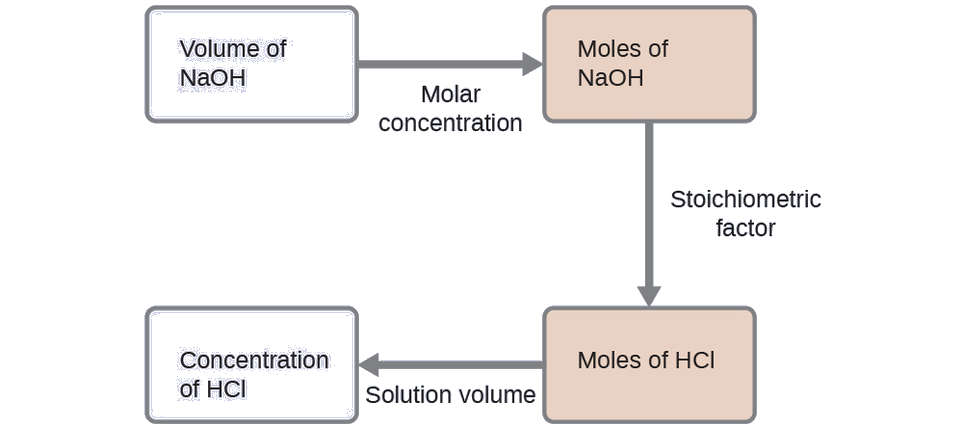
The molar amount of HCl is calculated to be:

\[\mathrm{35.23\:\cancel{mL\: NaOH}\times \dfrac{1\:\cancel{L}}{1000\:\cancel{mL}}\times \dfrac{0.250\:\cancel{mol\: NaOH}}{1\:\cancel{L}}\times \dfrac{1\: mol\: HCl}{1\:\cancel{mol\: NaOH}}=8.81\times 10^{-3}\:mol\: HCl}\]

Using the provided volume of HCl solution and the definition of molarity, the HCl concentration is:

\[\begin{align*}
M&=\mathrm{\dfrac{mol\: HCl}{L\: solution}}\\
M&=\mathrm{\dfrac{8.81\times 10^{-3}\:mol\: HCl}{50.00\: mL\times \dfrac{1\: L}{1000\: mL}}}\\
M&=0.176\:M
\end{align*}\]

Note: For these types of titration calculations, it is convenient to recognize that solution molarity is also equal to the number of millimoles of solute per milliliter of solution:

\[M=\mathrm{\dfrac{mol\: solute}{L\: solution}\times \dfrac{\dfrac{10^3\:mmol}{mol}}{\dfrac{10^3\:mL}{L}}=\dfrac{mmol\: solute}{mL\: solution}}\]

Using this version of the molarity unit will shorten the calculation by eliminating two conversion factors:

\[\mathrm{\dfrac{35.23\:mL\: NaOH\times \dfrac{0.250\:mmol\: NaOH}{mL\: NaOH}\times \dfrac{1\:mmol\: HCl}{1\:mmol\: NaOH}}{50.00\:mL\: solution}=0.176\: \mathit M\: HCl}\]

Exercise \(\PageIndex{1}\)

A 20.00-mL sample of aqueous oxalic acid, H₂C₂O₄, was titrated with a 0.09113-M solution of potassium permanganate, KMnO₄.

\[\ce{2MnO4-}(aq)+\ce{5H2C2O4}(aq)+\ce{6H+}(aq)\rightarrow \ce{10CO2}(g)+\ce{2Mn^2+}(aq)+\ce{8H2O}(l)\]

A volume of 23.24 mL was required to reach the end point. What is the oxalic acid molarity?

Answer: 0.2648 M

Summary

The stoichiometry of chemical reactions may serve as the basis for quantitative chemical analysis methods. Titrations involve measuring the volume of a titrant solution required to completely react with a sample solution. This volume is then used to calculate the concentration of analyte in the sample using the stoichiometry of the titration reaction. Gravimetric analysis involves separating the analyte from the sample by a physical or chemical process, determining its mass, and then calculating its concentration in the sample based on the stoichiometry of the relevant process. Combustion analysis is a gravimetric method used to determine the elemental composition of a compound by collecting and weighing the gaseous products of its combustion.

Glossary

analyte: chemical species of interest

buret: device used for the precise delivery of variable liquid volumes, such as in a titration analysis

combustion analysis: gravimetric technique used to determine the elemental composition of a compound via the collection and weighing of its gaseous combustion products

end point: measured volume of titrant solution that yields the change in sample solution appearance or other property expected for stoichiometric equivalence (see equivalence point)

equivalence point: volume of titrant solution required to react completely with the analyte in a titration analysis; provides a stoichiometric amount of titrant for the sample’s analyte according to the titration reaction; indicator

substance added to the sample in a titration analysis to permit visual detection of the end point

quantitative analysis: the determination of the amount or concentration of a substance in a sample

titrant: solution containing a known concentration of substance that will react with the analyte in a titration analysis

titration analysis: quantitative chemical analysis method that involves measuring the volume of a reactant solution required to completely react with the analyte in a sample

Contributors

Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).