5.7: Properties of Unit Cells
- Page ID
- 460914
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Size of a Metallic Unit Cell
The size of a cubic unit cell is describe by the length of the side of the unit cell and by the volume of the unit cell. The length of the side of the unit cell depends on the radius of the atoms contained in the unit cell and on the arrangement of the atoms in the unit cell (the structure of the unit cell). The mathemetical relationship between side length and atomic radius is derived below for the simple cubic, face-centered cubic, and body-centered cubic unit cells.
The sides of a cubic unit cell are all equal in length. Therefore, the volume of the unit cell is given by the volume of a cube: \(\ce_V=l^3\).
A note on units
Atomic and ionic radii are typically reported in units of picometers (pm, 10-12 m) or angstroms (Å, 10-10 m).
Simple Cubic
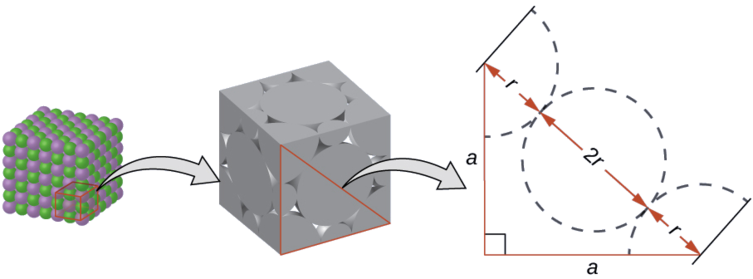
In a simple cubic unit cell, the corner atoms are in physical contact along the edge of the unit cell. Each side length is made up of two radii.
The length of a side is given as: \(\ce_l=2r\).
Volume of the unit cell is given as: \(\ce_V=(2r)^3=8r^3\).
 Figure \(\PageIndex{1}\): Simple cubic unit cell demonstrating the relationship between atomic radius and side length. (CC-BY-NC-SA 4.0; Kathryn A. Newton)
Figure \(\PageIndex{1}\): Simple cubic unit cell demonstrating the relationship between atomic radius and side length. (CC-BY-NC-SA 4.0; Kathryn A. Newton)Face-Centered Cubic
In a face-centered cubic unit cell, each corner atom is in physical contact the face atoms, and therefore, is not in physical contact with any of the other corner atoms. The diagonal across each face of the unit cell is made up of four radii (two corner atom radii and two face atom radii). The length of the face diagonal is given as: \(\ce_d=4r\). Two edges of the unit cell make a right triangle with the diagonal across the face of the unit cell. Thus, the relationship between atomiside length of the unit cell can be derived using the Pythagorean theorem:
\[\ce_d^2=l^2+l^2=2l^2 \nonumber\]
\[\ce_(4r)^2=2l^2 \nonumber\]
\[\ce_16r^2=2l^2 \nonumber\]
\[\ce_\sqrt{8r^2}=\sqrt{l^2} \nonumber\]
The length of a side is given as: \(\ce_\sqrt{8}r=l \nonumber\).
Volume of the unit cell is given as: \(\ce_V=l^3=(\sqrt{8}r)^3=8\sqrt{8}r^3 \nonumber\).

(a)

(b)

(c)
Body-Centered Cubic
In a body-centered cubic unit cell, each corner atom is in physical contact the body atom, and therefore, is not in physical contact with any of the other corner atoms. Two sides of the unit cell make a right triangle with the diagonal across the face of the unit cell. The diagonal through the body of the unit cell is made up of four radii (two corner atom radii and two body atom radii) and is the hypotenuse of the right triangle made by one edge of the unit cell and the diagonal across the face of the unit cell. The body hypotenuse is given as: \(\ce_h=4r\). Using these two right triangles, the relationship between atomic radius and side length of the unit cell can be derived using the Pythagorean theorem:
\[\ce_d^2=l^2+l^2=2l^2 \nonumber\]
\[\ce_h^2=l^2+d^2 \nonumber\]
\[\ce_h^2=l^2+2l^2 \nonumber\]
\[\ce_(4r)^2=3l^2 \nonumber\]
\[\ce_16r^2=3l^2 \nonumber\]
\[\ce_\sqrt{16r^2}=\sqrt{3l^2} \nonumber\]
\[\ce_4r=\sqrt{3}l \nonumber\]
The length of a side is given as: \(\ce_\frac{4r}{\sqrt{3}}=l \nonumber\).
Volume of the unit cell is given as: \(\ce_V=l^3=(\frac{4r}{\sqrt{3}})^3=\frac{64}{3\sqrt{3}}r^3 \nonumber\).

(a)

(b)

(c)

(c)
The edge length of the unit cell of alpha polonium is 336 pm. Determine the radius of a polonium atom.
Solution
Alpha polonium crystallizes in a simple cubic unit cell. Two adjacent Po atoms contact each other, so the edge length of this cell is equal to two Po atomic radii: \(l = 2r\). Therefore, the radius of Po is
\[r=\mathrm{\dfrac{l}{2}=\dfrac{336\: pm}{2}=168\: pm}\nonumber \]
Calcium crystallizes in a face-centered cubic structure. The edge length of its unit cell is 558.8 pm. What is the atomic radius of Ca in this structure?
Solution
In an FCC structure, Ca atoms contact each other across the diagonal of the face, so the length of the diagonal is equal to four Ca atomic radii (d = 4r).
Two adjacent edges and the diagonal of the face form a right triangle, with the length of each side equal to 558.8 pm and the length of the hypotenuse equal to four Ca atomic radii:
\[\begin{align*} a^2+a^2 &=d^2 \\[4pt] \mathrm{(558.8\:pm)^2+(558.5\:pm)^2} &=(4r)^2 \end{align*} \nonumber \]
Solving this gives
\[r=\mathrm{\sqrt{\dfrac{(558.8\:pm)^2+(558.5\:pm)^2}{16}}}=\textrm{197.6 pmg for a Ca radius}. \nonumber \]
Size of an Ionic Unit Cell
Similar to a metallic unit cell, the length of the side of an ionic unit cell depends on the radius of the atoms contained in the unit cell and on the arrangement of the atoms in the unit cell (the structure of the unit cell). There are two difference when finding the size of an ionic unit cell. First, there will be two or more radii to consider, and second, the location of each atom (type of radii) needs to be considered. The relationship between side length and atomic radii can be derived by drawing analogy to the metallic unit cell structures and adjusting for having multiple values for the radii. A few derivations are shown below for various ionic unit cells.
It is important to realize that values for ionic radii calculated from the edge lengths of unit cells depend on numerous assumptions, such as a perfect spherical shape for ions, which are approximations at best. Hence, such calculated values are themselves approximate and comparisons cannot be pushed too far. Nevertheless, this method has proved useful for calculating ionic radii from experimental measurements such as X-ray crystallographic determinations.
Cesium Chloride (CsCl)
In a cesium chloride structure, the chloride ions form a simple cubic lattice and the cesium ions occupy 100% of the cubic interstitial sites. Each chloride corner is in contact with the cesium body atom in a structure analogous to the body-centered cubic unit cell (Figure \(\PageIndex{3}\)). The diagonal through the body of the unit cell is made up of four radii: two chloride corner atom radii and two cesium body atom radii. The body diagonal is the hypotenuse of a right triangle made by one edge of the unit cell and the diagonal across the face of the unit cell. The body hypotenuse is given as: \(\ce_h=2r_1+2r_2\), where \(\ce_r_1\) and \(\ce_r_2\) are the radii of the anions and cations. Using these two right triangles, the relationship between atomic radius and side length of the unit cell can be derived using the Pythagorean theorem:
\[\ce_d^2=l^2+l^2=2l^2 \nonumber\]
\[\ce_h^2=l^2+d^2 \nonumber\]
\[\ce_h^2=l^2+2l^2 \nonumber\]
\[\ce_(2r_1+2r_2)^2=3l^2 \nonumber\]
\[\ce_\sqrt{(2r_1+2r_2)^2}=\sqrt{3l^2} \nonumber\]
\[\ce_2r_1+2r_2=\sqrt{3}l \nonumber\]
The length of a side is given as: \(\ce_\frac{(2r_1+2r_2)}{\sqrt{3}}=l \nonumber\).
Volume of the unit cell is given as: \(\ce_V=l^3=(\frac{(2r_1+2r_2)}{\sqrt{3}})^3=\frac{(2r_1+2r_2)^3}{3\sqrt{3}} \nonumber\).

Lithium Chloride (LiCl)
In a lithium chloride structure, the chloride ions form a face-centered cubic lattice and the lithium ions occupy 100% of the octahedral interstitial sites. When looking at a unit cell, there will be a lithium ion in the body position and on each edge of the unit cell. The lithium ions are small enough that the corner chloride ions are in physical contact with the face chloride ions. The corner chloride ions are not in physical contact with any of the other corner ions.
The diagonal across each face of the unit cell is made up of four radii (two corner chloride ion radii and two face chloride ion radii). The length of the face diagonal is given as: \(\ce_d=4r_1\), where \(\ce_r_1\) is the ionic radius of the corner ion (chloride). Two edges of the unit cell make a right triangle with the diagonal across the face of the unit cell. Thus, the relationship between the ionic radii and the side length of the unit cell can be derived using the Pythagorean theorem:
\[\ce_d^2=l^2+l^2=2l^2 \nonumber\]
\[\ce_(4r_1)^2=2l^2 \nonumber\]
\[\ce_16r_1^2=2l^2 \nonumber\]
\[\ce_\sqrt{8r_1^2}=\sqrt{l^2} \nonumber\]
The length of a side is given as: \(\ce_\sqrt{8}r_1=l \nonumber\).
Volume of the unit cell is given as: \(\ce_V=l^3=(\sqrt{8}r_1)^3=8\sqrt{8}r_1^3 \nonumber\).
 (a)
(a) (b)
(b)Sodium Chloride (NaCl)
In a sodium chloride structure, the chloride ions form a face-centered cubic lattice and the sodium ions occupy 100% of the octahedral interstitial sites. When looking at a unit cell, there will be a sodium ion in the body position and on each edge of the unit cell. The sodium ions are large enough that the corner chloride ions are not in physical contact with the face chloride ions but do make contact with the edge sodium ions.
The edge of the unit cell is made up of four radii (two corner chloride ion radii and two edge sodium ion radii).
The length of a side of the unit cells is given as: \(\ce_l=2r_1+2r_2=2(r_1+r_2)\), where \(\ce_r_1\) is the ionic radius of the corner ion (chloride) and \(\ce_r_2\) is the ionic radius of the edge ion (sodium).
Volume of the unit cell is given as: \(\ce_V=l^3=(2(r_1+r_2))^3=8(r_1+r_2)^3 \nonumber\).
 (a)
(a) (b)
(b)The edge length of the unit cell of LiCl (NaCl-like structure, FCC) is 0.514 nm or 5.14 Å. Assuming that the lithium ion is small enough so that the chloride ions are in contact, calculate the ionic radius for the chloride ion. Note: The length unit angstrom, Å, is often used to represent atomic-scale dimensions and is equivalent to 10−10 m.
Solution
On the face of a LiCl unit cell, chloride ions contact each other across the diagonal of the face:
Drawing a right triangle on the face of the unit cell, we see that the length of the diagonal is equal to four chloride radii (one radius from each corner chloride and one diameter—which equals two radii—from the chloride ion in the center of the face), so \(d = 4r\). From the Pythagorean theorem, we have:
\[a^2+a^2=d^2 \nonumber \]
which yields:
\[\mathrm{(0.514\:nm)^2+(0.514\:nm)^2}=(4r)^2=16r^2 \nonumber \]
Solving this gives:
\[r=\mathrm{\sqrt{\dfrac{(0.514\:nm)^2+(0.514\:nm)^2}{16}}=0.182\: nm\:(1.82\: Å)\:for\: a\: Cl^−\: radius.} \nonumber \]
Density of a Unit Cell
By definition, the density of an object is equal to the mass of the object divided by its volume and is given by the equation:
\[\ce_d=\frac{m}{V} \nonumber\]
For a crystalline solid, the volume of the unit cell, and therefore the density of the solid, depend on the arrangement of atoms in in the lattice structure. Methods to calculate the volume of a cubic unit cells are discussed above. The mass of a cubic unit cell depends on the number of atoms contained in the unit cell and the mass of those atoms.
The steps to find the mass of a unit cell are as follows:
- Determine the mass of a single atom of each element in the unit cell by dividing the respective molar mass by Avogadro's number.
- Determine how many atoms or ions are contained in the unit cell structure.
- Multiply the mass of one atom by the number of atoms in the unit cell structure for each element in the structure.
- Sum the collected masses of all elements to find the overall mass of the unit cell.
The mass of the unit cell can then be used to calculate the density of the unit cell by dividing by the unit cell volume.
Platinum crystallizes in a face-centered cubic structure. The molar mass of platinum is 195.084 g/mol. Calculate the mass of one unit cell of platinum.
Solution
- Calculate mass of one atom of Pt.
\[\ce_\frac{195.084 g}{mol}\times\ \frac{mol}{6.022\times\ 10^{24} atoms}=3.240\times\ 10^{-23} g/atom \nonumber\]
- Determine how many atoms are in the unit cell.
Face-centered cubic structures contain 4 lattice atoms (8 x 1/8 corner atoms, 6 x 1/2 face atoms)
- Calculate the mass of atoms in the unit cell.
\[\ce_\frac{3.240\times\ 10^{-23} g}{atom} \times\ 4\ atoms = 1.30 \times\ 10^{-22} g \nonumber \]
The mass of one unit cell of platinum is 1.30 x 10-22 g
Determine the mass of one unit cell of sodium chloride. Sodium chloride crystallizes in a face-centered cubic lattice with the sodium atoms occupying 100% of the octahedral interstitial sites.
Solution
- Calculate mass of one atom of Na and one atom of Cl.
\[\ce_m_Na=\frac{22.99 g}{mol}\times\ \frac{mol}{6.022\times\ 10^{24} atoms}=3.818\times\ 10^{-23} g/atom \nonumber\]
\[\ce_m_Cl=\frac{35.45 g}{mol}\times\ \frac{mol}{6.022\times\ 10^{24} atoms}=5.887\times\ 10^{-23} g/atom \nonumber\]
- Determine how many atoms are in the unit cell.
Face-centered cubic structures contain 4 lattice atoms (8 x 1/8 corner atoms, 6 x 1/2 face atoms) and 4 octahedral interstitial sites. There will be 4 chloride ions and 4 sodium ions (100% occupancy).
- Calculate the mass of atoms in the unit cell.
\[\ce_m_{unit\ cell}=(4 \times\ m_{Na}) + (4 \times\ m_{Cl}) \nonumber\]
\[\ce_m_{unit\ cell}=(4 \times\ 3.818\times\ 10^{-23} g) + (4 \times\ 5.887\times\ 10^{-23} g) \nonumber\]
\[\ce_m_{unit\ cell}= 9.704 \times\ 10^{-23} g \nonumber\]
The mass of one unit cell of platinum is 9.704 x 10-23 g
Problems
Silver crystallizes in an FCC structure. The edge length of its unit cell is 409 pm.
- What is the atomic radius of Ag in this structure?
- Calculate the density of Ag.
- Answer a
-
144 pm
- Answer b
-
10.5 g/cm3
The edge length of the unit cell for nickel is 0.3524 nm. The density of Ni is 8.90 g/cm3. Does nickel crystallize in a simple cubic structure? Explain.
- Answer
-
No. If Ni were simple cubic, its density would be given by:
\[\mathrm{1\: Ni\: atom×\dfrac{1\: mol\: Ni}{6.022\times 10^{23}\:Ni\: atoms}×\dfrac{58.693\:g}{1\: mol\: Ni}=9.746\times 10^{−23}\:g}\nonumber \]
\[V=l^3=\mathrm{(3.524\times 10^{−8}\:cm)^3=4.376\times 10^{−23}\:cm^3}\nonumber \]
Then the density of Ni would be
\[(\mathrm{=\dfrac{9.746\times 10^{−23}\:g}{4.376\times 10^{−23}\:cm^3}=2.23\: g/cm^3}\nonumber \]
Since the actual density of Ni is not close to this, Ni does not form a simple cubic structure.
The edge length of the unit cell of KCl (NaCl-like structure, FCC) is 6.28 Å. Assuming anion-cation contact along the cell edge, calculate the radius of the potassium ion. The radius of the chloride ion is 1.82 Å.
- Answer
-
The radius of the potassium ion is 1.33 Å.
Calcium crystallizes in a face-centered cubic structure. The edge length of its unit cell is 558.8 pm. Calculate the density of Ca.
- Answer
-
Density is given by \(\mathrm{density=\dfrac{mass}{volume}}\). The density of calcium can be found by determining the density of its unit cell: for example, the mass contained within a unit cell divided by the volume of the unit cell. A face-centered Ca unit cell has one-eighth of an atom at each of the eight corners (\(8 \times \dfrac{1}{8}=1\)atom) and one-half of an atom on each of the six faces \(6×\dfrac{1}{2}=3\) atoms), for a total of four atoms in the unit cell.
The mass of the unit cell can be found by:
\[\mathrm{1\: Ca\: unit\: cell×\dfrac{4\: Ca\: atoms}{1\: Ca\: unit\: cell}×\dfrac{1\: mol\: Ca}{6.022\times 10^{23}\:Ca\: atoms}×\dfrac{40.078\:g}{1\: mol\: Ca}=2.662\times 10^{−22}\:g} \nonumber \]
The volume of a Ca unit cell can be found by:
\[V=a^3=\mathrm{(558.8\times 10^{−10}\:cm)^3=1.745\times 10^{−22}\:cm^3} \nonumber \]
(Note that the edge length was converted from pm to cm to get the usual volume units for density.)
Then, the density of polonium:
\[\mathrm{Po=\dfrac{2.662\times 10^{−22}\:g}{1.745\times 10^{−22}\:cm^3}=1.53\: g/cm^3} \nonumber \]
The edge length of the unit cell of alpha polonium is 336 pm. Determine the density of alpha polonium.
- Answer
-
Density is given by
\[\mathrm{density=\dfrac{mass}{volume}}.\nonumber \]
The density of polonium can be found by determining the density of its unit cell (the mass contained within a unit cell divided by the volume of the unit cell). Since a Po unit cell contains one-eighth of a Po atom at each of its eight corners, a unit cell contains one Po atom.
The mass of a Po unit cell can be found by:
\[\mathrm{1\: Po\: unit\: cell×\dfrac{1\: Po\: atom}{1\: Po\: unit\: cell}×\dfrac{1\: mol\: Po}{6.022\times 10^{23}\:Po\: atoms}×\dfrac{208.998\:g}{1\: mol\: Po}=3.47\times 10^{−22}\:g}\nonumber \]
The volume of a Po unit cell can be found by:
\[V=l^3=\mathrm{(336\times 10^{−10}\:cm)^3=3.79\times 10^{−23}\:cm^3}\nonumber \]
(Note that the edge length was converted from pm to cm to get the usual volume units for density.)
Therefore, the density of
\[\mathrm{Po=\dfrac{3.471\times 10^{−22}\:g}{3.79\times 10^{−23}\:cm^3}=9.16\: g/cm^3}\nonumber \]

