2.5.2: Cations Act as Brønsted Acids in Water

Metal cations act as acids by polarizing bound water molecules called aqua ligands

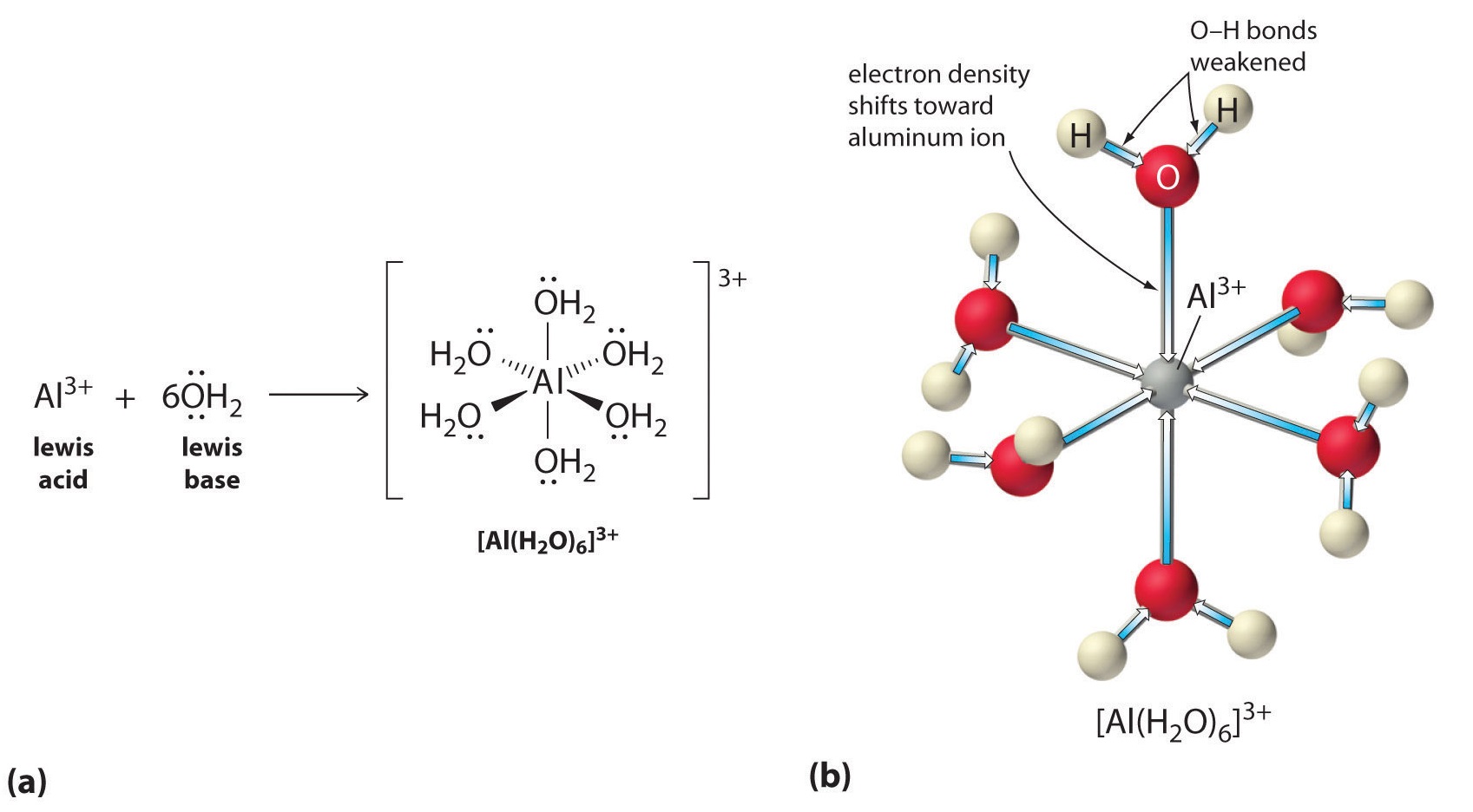
Aqueous solutions of simple salts of metal ions can also be acidic, even though a metal ion cannot donate a proton directly to water to produce \(H_3O^+\). Instead, a metal ion can act as a Lewis acid and interact with water, a Lewis base, by coordinating to a lone pair of electrons on the oxygen atom to form a hydrated metal ion.

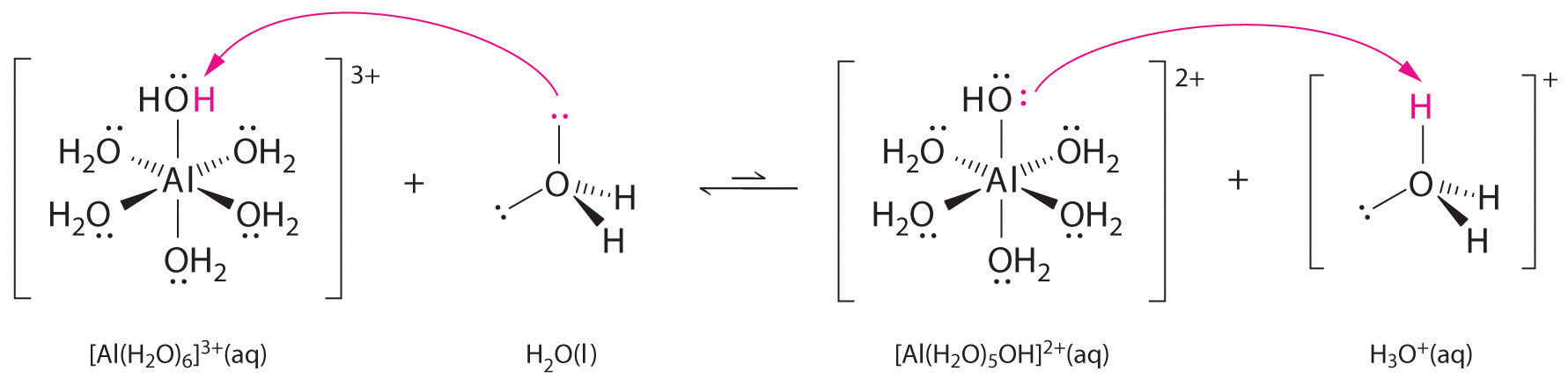
A water molecule coordinated to a metal ion is more acidic than a free water molecule for two reasons. First, repulsive electrostatic interactions between the positively charged metal ion and the partially positively charged hydrogen atoms of the coordinated water molecule make it easier for the coordinated water to lose a proton.

Second, the positive charge on the \(Al^{3+}\) ion attracts electron density from the oxygen atoms of the water molecules, which decreases the electron density in the \(\ce{O–H}\) bonds, as shown in Figure \(\PageIndex{1b}\). With less electron density between the \(O\) atoms and the H atoms, the \(\ce{O–H}\) bonds are weaker than in a free \(H_2O\) molecule, making it easier to lose an \(H^+\) ion. This is shown schematically in Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\): Effect of a Metal Ion on the Acidity of Water (a) Reaction of the metal ion \(Al^{3+}\) with water to form the hydrated metal ion is an example of a Lewis acid–base reaction. (b) The positive charge on the aluminum ion attracts electron density from the oxygen atoms, which shifts electron density away from the O–H bonds. The decrease in electron density weakens the O–H bonds in the water molecules and makes it easier for them to lose a proton. (CC BY-NC-SA 3.0; anonymous)

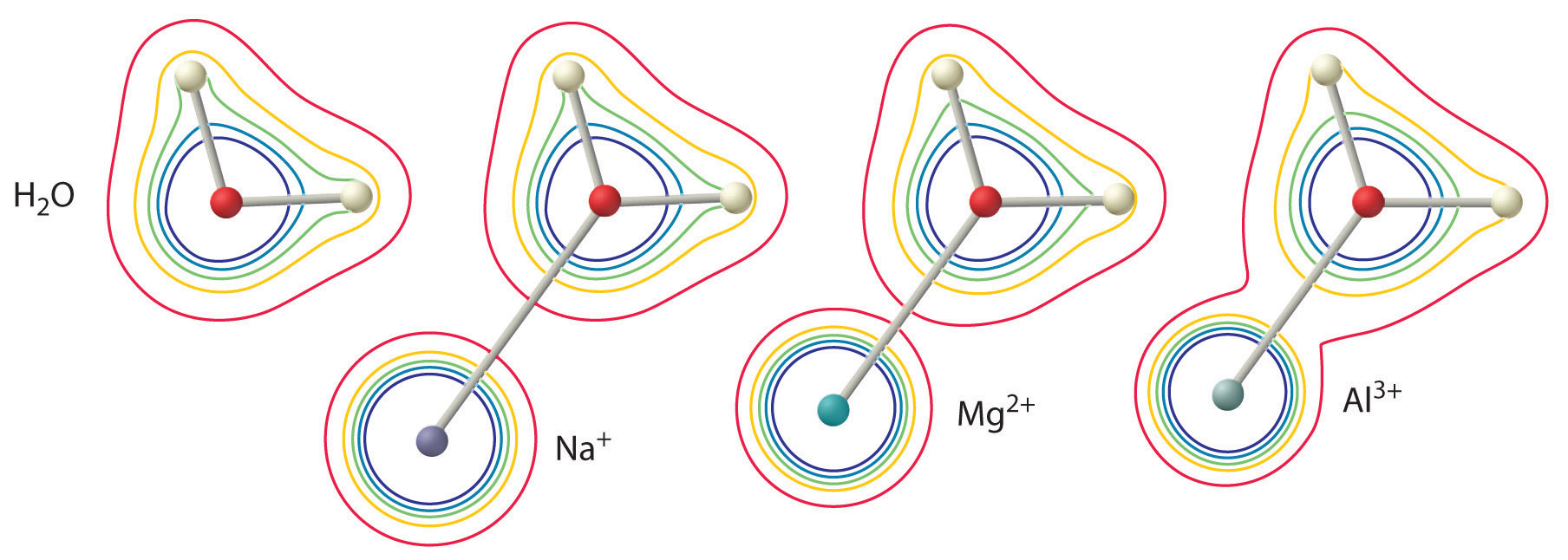
Acidity depends primarily on the charge to size ratio

The degree of acidity of a  metal cation depends on the charge on the metal ion and the radius of the metal ion (Figure \(\PageIndex{2}\)). A divalent ion (\(\ce{M^{2+}}\)) has approximately twice as strong an effect on the electron density in a coordinated water molecule as a monovalent ion (\(\ce{M^{+}}\)). For metal ions with the same charge, the smaller the ion, the shorter the internuclear distance to the oxygen atom of the water molecule and the greater the effect of the metal on the electron density distribution in the water molecule.

Figure \(\PageIndex{2}\): The effect of the charge and radius of a metal ion on the acidity of a coordinated water molecule. The contours show the electron density on the O atoms and the H atoms in both a free water molecule (left) and water molecules coordinated to \(Na^+\), \(Mg^{2+}\), and \(Al^{3+}\) ions. These contour maps demonstrate that the smallest, most highly charged metal ion (\(Al^{3+}\)) causes the greatest decrease in electron density of the O–H bonds of the water molecule. Due to this effect, the acidity of hydrated metal ions increases as the charge on the metal ion increases and its radius decreases. (CC BY-NC-SA 3.0; anonymous)

The charge to size ratio explains why most alkali metal cations exhibit little acidity while aqueous solutions of small, highly charged metal ions, such as \(Al^{3+}\) and \(Fe^{3+}\), are acidic:

\[\ce {[Al(H2O)6]^{3+}(aq) <=> [Al(H2O)5(OH)]^{2+}(aq) + H^{+}(aq)} \]

The \(\ce{[Al(H2O)6]^{3+}}\) ion has a \(pK_a\) of 5.0, making it almost as strong an acid as acetic acid. Because of the two factors described previously, the most important parameters for predicting the effect of a metal ion on the acidity of coordinated water molecules are the charge and ionic radius of the metal ion.

A simple empirical equation for predicting the pK_a of metal ions in water has been proposed by Wulfsberg:¹

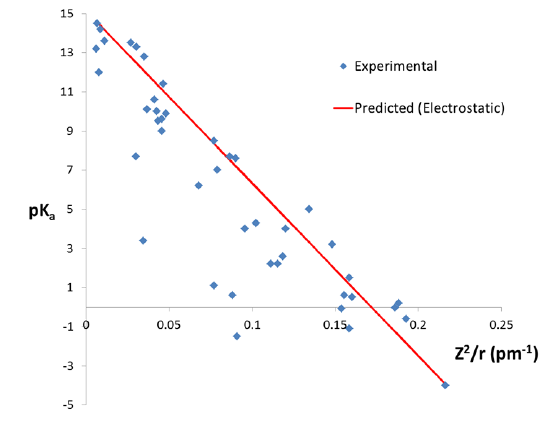
\[pK_a = 15.14 - 88.16~pm \left( \frac{Z^2}{r} \right) \]

where \(Z\) is the charge on the metal ion and \(r\) its radius. As can be seen from figure \(\PageIndex{3}\), in general the acidity of metal ions increases with \( \frac{Z^2}{r}) \). Nevertheless a number of ions have considerably lower \(pK_a\) values than predicted from this correlation, suggesting that the acidity of metal cations cannot be predicted using a simple electrostatic model alone.

Figure \(\PageIndex{3}\): The \(pK_a\) of metal ions (♦) as a function of \( \frac{Z^2}{r} \) for 43 metal ions. Drawn using radii listed in reference 1.

Although the charge-to-size ratio is the simplest and most powerful predictor of metal ion acidity in water, three additional factors also can play a role:

Other Factors Affecting Acidity

Electronegativity

All other things being equal, more electronegative elements are better able to withdraw electron density from a bound water ligand and consequently better at enhancing the ability of that water molecule to lose a hydrogen ion. The electrostatic model of ion acidity can be extended to account for electronegativity effects but only needs to be done so for metals with Pauling electronegativities greater than 1.5. The empirical relationship that has been proposed to account for the effect of electronegativity is:

\[pK_a = 15.14 - 88.16 \left( \frac{Z^2}{r} + 0.096( \chi - 1.50) \right) \]

where \(r\) is the ion radius in pm and \( \chi \) is its Pauling electronegativity. As can be seen from figure \(\PageIndex{4}\), the electronegativity term accounts for some of the deviations in metal ion acidity predicted from charge and size effects alone.

Figure \(\PageIndex{4}\): Comparison between the experimental \(pK_a\) values (♦) for 43 metal ions and those predicted empirically accounting for size and charge effects ( -) and accounting for size, charge, and electronegativity effects (♦). Drawn using radii listed in reference 1.

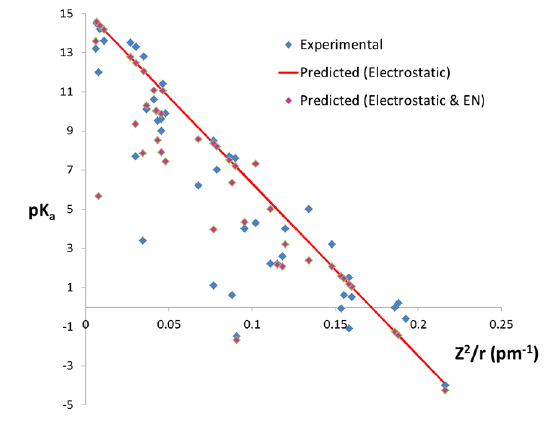
However, there are still large deviations between the predicted and observed pK_a for a number of ions. In particular, the modified electrostatic model overestimates the pK_a of Al³⁺ and Sn⁴⁺ and underestimates the pK_a of Hg²⁺, Sn²⁺, and Tl³⁺. While the exact reasons for these discrepancies is not entirely clear, at least some are thought to arise from the impact of the fourth factor that determines metal ion acidity.

Hardness and Softness

Cation hardness or softness is assessed according to Pearson's Hard-Soft Acid Base Principle (HSABP). In general, soft cations are more acidic than hard cations of the same charge and radius, as may be seen from the examples in Table \(\PageIndex{1}\). The greater than expected acidity of softer cations is thought to reflect the importance of covalent contributions to the metal-water bond.

Table \(\PageIndex{1}\): Comparison of the \(pK_a\) values at 25°C of hard and soft cations with approximately the same radius and charge. Based on Gutmann² as reported by Burgess.³

Cation	Classification	Radius (pm)	\(pK_a1\)
\(K^+\)	hard	1.33	14
\(Ag^+\)	soft	1.26	10
\(Mg^{2+}\)	hard	0.65	12.2
\(Cu^{2+}\)	soft	0.69	7.3
\(Ca^{2+}\)	hard	0.99	12.6
\(Cd^{2+}\)	soft	0.97	9.0
\(Sr^{2+}\)	hard	1.13	13.1
\(Hg^{2+}\)	soft	1.10	3.6

References

1. Wulfsberg, G. Principles of Descriptive Inorganic Chemistry University Science Books, 1991, pp. 28-30.
2. (a) Gutmann, V. Allg. Prakt. Chem. 1970, 21, 116. (b) Gutmann, V. Fortschr. Chem. Forsch. 1972, 27, 59.
3. Burgess, J. Metal Ions in Solution Ellis Horwood, 1978, pg. 268.