1.2: Quantum Numbers
- Page ID
- 447975
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Estimated Time to Read: 7 min
Quantum Numbers
Schrödinger’s approach uses four quantum numbers (n, l, ml, and ms) to specify any wavefunction. The first three quantum numbers (n, l, and ml) provide information about the spatial distribution of an electron. Although n can be any positive integer, only certain values of l, ml, and ms are allowed for a given value of n.
The Principal Quantum Number
The principal quantum number (n) tells the average relative distance of an electron from the nucleus. Its value can be any positive integer:
\[n = 1, 2, 3, 4,… \label{6.5.1} \]
As n increases for a given atom, so does the average distance of an electron from the nucleus. A negatively charged electron that is, on average, closer to the positively charged nucleus is attracted to the nucleus more strongly than an electron that is farther out in space. This means that electrons with higher values of n are easier to remove from an atom. All wavefunctions that have the same value of n are said to constitute a principal shell because those electrons have similar average distances from the nucleus. The principal quantum number n corresponds to the n used by Bohr to describe electron orbits and by Rydberg to describe atomic energy levels.
The Angular Momentum (or Azimuthal) Quantum Number
The angular momentum quantum number (l) describes the shape of the region of space occupied by the electron. The allowed values of l depend on the value of n and can range from 0 to n − 1:
\[l = 0, 1, 2,…, n − 1 \label{6.5.2} \]
For example, if n = 1, l can be only 0; if n = 2, l can be 0 or 1; and so forth.
For a given atom, all wavefunctions that have the same values of both n and l form a subshell. The regions of space occupied by electrons in the same subshell usually have the same shape, but they are oriented differently in space.
Principal quantum number (n) and angular momentum (l): The Orbital Subshell: Principal quantum number (n) and angular momentum (l): The Orbital Subshell [youtu.be]
The Magnetic Quantum Number
The magnetic quantum number (ml) describes the orientation of the region in space occupied by an electron with respect to an applied magnetic field. The allowed values of ml depend on the value of l: ml can range from −l to l in integral steps:
\[m_l = −l, −l + 1,…, 0,…, l − 1, l \label{6.5.3} \]
For example, if l = 0, then ml can be only 0; if l = 1, ml can be −1, 0, or +1; and if l = 2, ml can be −2, −1, 0, +1, or +2.
Each wavefunction with an allowed combination of n, l, and ml values describes an atomic orbital, a particular spatial distribution for an electron. For a given set of quantum numbers, each principal shell has a fixed number of subshells, and each subshell has a fixed number of orbitals.
The Spin Quantum Number
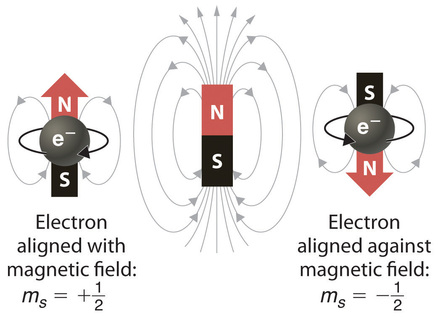
Scientists analyzed the emission and absorption spectra of the elements closely and saw that for elements having more than one electron, nearly all the lines in the spectra were actually pairs of very closely spaced lines. Each line in the spectra represents an energy level available to electrons in the atom; pairs of lines resulted in twice as many energy levels as would be predicted solely based on the quantum numbers \(n\), \(l\), and \(m_l\). Scientists also discovered that applying a magnetic field caused the lines in the pairs to split farther apart. In 1925, two graduate students in physics in the Netherlands, George Uhlenbeck (1900–1988) and Samuel Goudsmit (1902–1978), proposed that the splittings were caused by an electron spinning about its axis, much as Earth spins about its axis. When an electrically charged object spins, it produces a magnetic moment parallel to the axis of rotation, making it behave like a magnet. Although the electron cannot be viewed solely as a particle, spinning or otherwise, it is indisputable that it does have a magnetic moment. This magnetic moment is called electron spin.
In an external magnetic field, the electron has two possible orientations (Figure Figure \(\PageIndex{1}\)). It can align with the magnetic field or against it. These orientations are described by the spin quantum number, ms, which can have a value of +½ (spin up) and −½ (spin down) to indicate that the two orientations are opposites. The value of ms does not depend on the other three quantum numbers. Spin is significant in that it allows two electrons to occupy the same orbital. Two electrons can have the same values for n, l, and ml but opposite spin values that allow them to occupy the same orbital. Thus, each orbital can hold one pair of electrons, each with a different spin quantum number value. Every electron in an atom must have a unique set of quantum number. If n, m, and l are the same for two electrons, then ms must be different.
Magnetic Quantum Number (ml) & Spin Quantum Number (ms): Magnetic Quantum Number (ml) & Spin Quantum Number (ms) [youtu.be]
How many subshells are contained within the principal shell with n = 3?
- Hint
-
Given n = 3, calculate the allowed values of l. From these allowed values, count the number of subshells.
- Answer
-
If n = 3, then l can equal 0, 1, or 2. Because the shell has four values of l, it has three subshells.
How many orbitals are contained within the principal shell with n = 3?
- Hint
-
For each allowed value of l, calculate the allowed values of ml. The sum of the number of orbitals in each subshell is the number of orbitals in the principal shell.
- Answer
-
If n = 3, then l can equal 0, 1, or 2.
When l = 0, then ml can be only 0. Thus, the l = 0 subshell has only one orbital.
When l = 1, then ml can be 0 or ±1. The l = 1 subshell has three orbitals.
When l = 2, then ml can be 0, ±1, or ±2. The l = 2 subshell has five orbitals
The total number of orbitals in the n = 3 principal shell is the sum of the number of orbitals in each subshell (1 + 3 + 5 = 9).
The total number of orbitals is equal to n2 (32 = 9).
How many orbitals are contained within the principal shell with n = 4?
- Hint
-
For each allowed value of l, calculate the allowed values of ml. The sum of the number of orbitals in each subshell is the number of orbitals in the principal shell.
- Answer
-
If n = 4, then l can equal 0, 1, 2, or 3.
When l = 0, then ml can be only 0. Thus, the l = 0 subshell has only one orbital.
When l = 1, then ml can be 0 or ±1. The l = 1 subshell has three orbitals.
When l = 2, then ml can be 0, ±1, or ±2. The l = 2 subshell has five orbitals
When l = 3, then ml can be 0, ±1, ±2, or ±3. The l = 3 subshell has seven orbitals.
The total number of orbitals in the n = 4 principal shell is the sum of the number of orbitals in each subshell (1 + 3 + 5 + 7 = 16) and is also equal to n2 (42 = 16)
How many orbitals are contained within the subshell with l = 5?
- Hint
-
For the specified value of l, calculate the allowed values of ml.
- Answer
-
If l = 5, then ml can equal 0, ±1, ±2, ±3, ±4, ±5. Thus, the l = 5 subshell has eleven orbitals.
The total number of orbitals is equal to 2l + 1 ((2 x 5) + 1 = 11).
Describing an Orbital
Each orbital in an atom is described by a set of three values for n, l, and ml. Typically when defining an orbital scientists will use an abbreviated system to refer to an orbital or subshell, rather than specifying the values of n, l , and ml.
In this system, the principal quantum number n is named first and is followed by a lowercase letter to denote the value of the angular momentum quantum number l (Table \(\PageIndex{1}\)) (These orbital designations are derived from historical terms for corresponding spectroscopic characteristics: sharp, principle, diffuse, and fundamental.)
| l | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| abbreviation | s | p | d | f |
A 2p subshell has n = 2 and l = 1. A 2p subshell has three orbitals, which correspond to ml = −1, 0, and +1. In the abbreviatiod system, the three orbitals are denoted with a subscript lower case letter that represents an orientation in space (Table \(\PageIndex{2}\)). For a 2p subshell, the three orbitals are denoted as 2px, 2py, and 2pz. The correlation between ml and a specific orientation in space is beyond the scope of this course.
| l | ml | abbreviation |
|---|---|---|
| 2 (p) | 0, ±1 | x, y, z |
| 3 (d) | 0, ±1, ±2 | xz, yz, xy, x2-y2, z2 |
Summary
Each principal shell has n subshells
For n = 1, only a single subshell is possible (1s). For n = 2, there are two subshells (2s and 2p). For n = 3, there are three subshells (3s, 3p, and 3d).
Every shell has an ns subshell. Any shell with n ≥ 2 also has an np subshell, and any shell with n ≥ 3 also has an nd subshell.
Each subshell has 2l + 1 orbitals
All ns subshells contain a single s orbital, all np subshells contain three p orbitals, all nd subshells contain five d orbitals, and all nf subshells contain seven f orbitals.
List all the allowed combinations of the four quantum numbers (n, l, ml, ms) for electrons in a 2p orbital and predict the maximum number of electrons the 2p subshell can accommodate.
- Hint
-
List the quantum numbers (n, l) that correspond to an n = 2p orbital. Then list the allowed combinations of n, l, and ml. Use the allowed values of ms to determine the maximum number of electrons in each 2p subshell.
- Answer
-
For a 2p orbital, we know that n = 2, l = 1, and ml = −l, (−l +1),…, (l − 1), l. There are only three possible combinations of (n, l, ml): (2, 1, 1), (2, 1, 0), and (2, 1, −1). Because ms is independent of the other quantum numbers and can have values of only +½ and −½, there are six possible combinations of (n, l, ml, ms): (2, 1, 1, +½), (2, 1, 1, −½), (2, 1, 0, +½), (2, 1, 0, −½), (2, 1, −1, +½), and (2, 1, −1, −½). Hence the 2p subshell, which consists of three 2p orbitals (2px, 2py, and 2pz), can contain a total of six electrons, two in each orbital.
List all the allowed combinations of the four quantum numbers (n, l, ml, ms) for a 6s orbital, and predict the total number of electrons it can contain.
- Hint
-
List the quantum numbers (n, l) that correspond to an n = 6s orbital. Then list the allowed combinations of n, l, and ml. Use the allowed values of ms to determine the maximum number of electrons in each 6s subshell.
- Answer
-
For a 6s orbital, we know that n = 6, l = 0, and ml = −l, (−l +1),…, (l − 1), l. There is only one possible combinations of (n, l, ml): (6, 0, 0)Because ms is independent of the other quantum numbers and can have values of only +½ and −½, there are two possible combinations of (n, l, ml, ms): (6, 0, 0, +½) and (6, 0, 0, −½). Hence the 6s subshell, which consists of one 6s orbital and can contain a total of two electrons.

