10.4: Atomic Absorption Spectroscopy

Guystav Kirchoff and Robert Bunsen first used atomic absorption spectroscopy—along with atomic emission—in 1859 and 1860 as a means for identify atoms in flames and hot gases. Although atomic emission continued to develop as an analytical technique, progress in atomic absorption languished for almost a century. Modern atomic absorption spectroscopy has its beginnings in 1955 as a result of the independent work of A. C. Walsh and C. T. J. Alkemade.¹³ Commercial instruments were in place by the early 1960s, and the importance of atomic absorption as an analytical technique was soon evident.

10.4.1 Instrumentation

Atomic absorption spectrophotometers use the same single-beam or double-beam optics described earlier for molecular absorption spectrophotometers (see Figure 10.26 and Figure 10.27). There is, however, an important additional need in atomic absorption spectroscopy—we must covert the analyte into free atoms. In most cases our analyte is in solution form. If our sample is a solid, then we must bring it into solution before the analysis. When analyzing a lake sediment for Cu, Zn, and Fe, for example, we bring the analytes into solution as Cu²⁺, Zn²⁺, and Fe³⁺ by extracting them with a suitable reagent. For this reason, only the introduction of solution samples is considered in this text.

Note

What reagent we choose to use depends on our research goals. If we need to know the total amount of metal in the sediment, then we might use a microwave digestion using a mixture of concentrated acids, such as HNO₃, HCl, and HF. This destroys the sediment’s matrix and brings everything into solution. On the other hand, if our interest is biologically available metals, we might extract the sample under milder conditions, such as a dilute solution of HCl or CH₃COOH at room temperature.

Atomization

The process of converting an analyte to a free gaseous atom is called atomization. Converting an aqueous analyte into a free atom requires that we strip away the solvent, volatilize the analytes, and, if necessary, dissociate the analyte into free atoms. Desolvating an aqueous solution of CuCl₂, for example, leaves us with solid particulates of CuCl₂. Converting the particulate CuCl₂ to gas phases atoms of Cu and Cl requires thermal energy.

\[\ce{CuCl}_{2(aq)} \rightarrow \ce{CuCl}_{2(s)} \rightarrow \ce{Cu}_{(g)} + \ce{2Cl}_{(g)}\]

There are two common atomization methods: flame atomization and electrothermal atomization, although a few elements are atomized using other methods.

Flame Atomizer

Figure 10.42 shows a typical flame atomization assembly with close-up views of several key components. In the unit shown here, the aqueous sample is drawn into the assembly by passing a high-pressure stream of compressed air past the end of a capillary tube immersed in the sample. When the sample exits the nebulizer it strikes a glass impact bead, converting it into a fine aerosol mist within the spray chamber. The aerosol mist is swept through the spray chamber by the combustion gases—compressed air and acetylene in this case—to the burner head where the flame’s thermal energy desolvates the aerosol mist to a dry aerosol of small, solid particles. The flame’s thermal energy then volatilizes the particles, producing a vapor consisting of molecular species, ionic species, and free atoms.

Note

Compressed air is one of the two gases whose combustion produces the flame.

Figure 10.42 Flame atomization assembly with expanded views of (a) the burner head showing the burner slot where the flame is located; (b) the nebulizer’s impact bead; and (c) the interior of the spray chamber. Although the unit shown here is from an older instrument, the basic components of a modern flame AA spectrometer are the same.

Burner. The slot burner in Figure 10.42a provides a long optical pathlength and a stable flame. Because absorbance increases linearly with the path length, a long path length provides greater sensitivity. A stable flame minimizes uncertainty due to fluctuations in the flame.

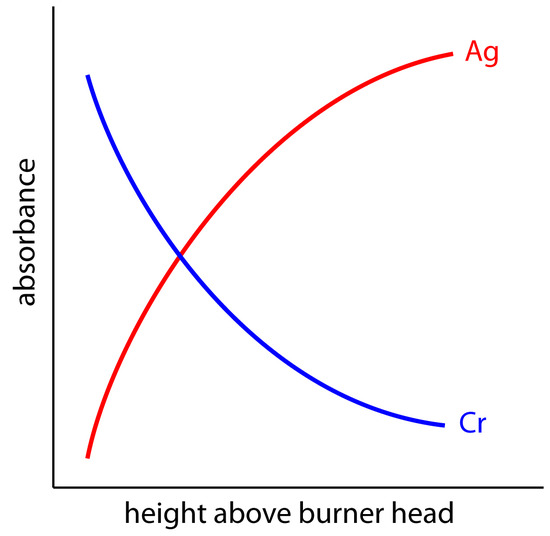
The burner is mounted on an adjustable stage that allows the entire assembly to move horizontally and vertically. Horizontal adjustments ensure that the flame is aligned with the instrument’s optical path. Vertical adjustments adjust the height within the flame from which absorbance is monitored. This is important because two competing processes affect the concentration of free atoms in the flame. The more time the analyte spends in the flame the greater the atomization efficiency; thus, the production of free atoms increases with height. On the other hand, a longer residence time allows more opportunity for the free atoms to combine with oxygen to form a molecular oxide. For an easily oxidized metal, such as Cr, the concentration of free atoms is greatest just above the burner head. For metals, such as Ag, which are difficult to oxidize, the concentration of free atoms increases steadily with height (Figure 10.43). Other atoms show concentration profiles that maximize at a characteristic height.

Figure 10.43 Absorbance versus height profiles for Ag and Cr in flame atomic absorption spectroscopy.

Flame. The flame’s temperature, which affects the efficiency of atomization, depends on the fuel–oxidant mixture, several examples of which are listed in Table 10.9. Of these, the air–acetylene and the nitrous oxide–acetylene flames are the most popular. Normally the fuel and oxidant are mixed in an approximately stoichiometric ratio; however, a fuel-rich mixture may be necessary for easily oxidized analytes.

Table 10.9 Fuels and Oxidants Used for Flame Combustion

fuel	oxidant	temperature range (^oC)
natural gas	air	1700–1900
hydrogen	air	2000–2100
acetylene	air	2100–2400
acetylene	nitrous oxide	2600–2800
acetylene	oxygen	3050–3150

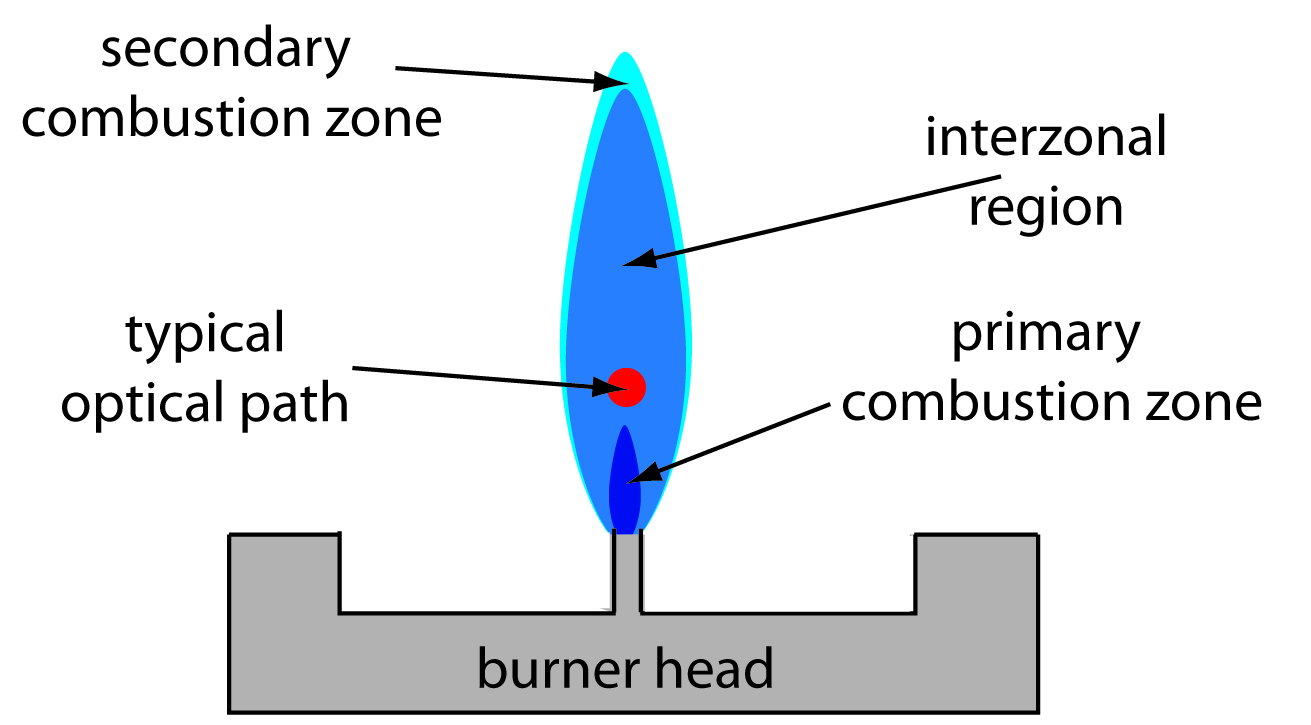
Figure 10.44 shows a cross-section through the flame, looking down the source radiation’s optical path. The primary combustion zone is usually rich in gas combustion products that emit radiation, limiting is usefulness for atomic absorption. The interzonal region generally is rich in free atoms and provides the best location for measuring atomic absorption. The hottest part of the flame is typically 2–3 cm above the primary combustion zone. As atoms approach the flame’s secondary combustion zone, the decrease in temperature allows for formation of stable molecular species.

Figure 10.44 Profile of typical flame using a slot burner. The relative size of each zone depends on many factors, including the choice of fuel and oxidant, and their relative proportions.

Sample Introduction. The most common means for introducing samples into a flame atomizer is a continuous aspiration in which the sample flows through the burner while we monitor the absorbance. Continuous aspiration is sample intensive, typically requiring from 2–5 mL of sample.

Flame microsampling allows us to introduce a discrete sample of fixed volume, and is useful when we have a limited amount of sample or when the sample’s matrix is incompatible with the flame atomizer. For example, continuously aspirating a sample that has a high concentration of dissolved solids—sea water, for example, comes to mind—may build-up a solid deposit on the burner head that obstructs the flame and that lowers the absorbance. Flame microsampling is accomplished using a micropipet to place 50–250 μL of sample in a Teflon funnel connected to the nebulizer, or by dipping the nebulizer tubing into the sample for a short time. Dip sampling is usually accomplished with an automatic sampler. The signal for flame microsampling is a transitory peak whose height or area is proportional to the amount of analyte that is injected.

Advantages and Disadvantages of Flame Atomization. The principal advantage of flame atomization is the reproducibility with which the sample is introduced into the spectrophotometer. A significant disadvantage to flame atomizers is that the efficiency of atomization may be quite poor. There are two reasons for poor atomization efficiency. First, the majority of the aerosol droplets produced during nebulization are too large to be carried to the flame by the combustion gases. Consequently, as much as 95% of the sample never reaches the flame. A second reason for poor atomization efficiency is that the large volume of combustion gases significantly dilutes the sample. Together, these contributions to the efficiency of atomization reduce sensitivity because the analyte’s concentration in the flame may be a factor of 2.5 × 10^–6 less than that in solution.¹⁴ This is the reason for the waste line shown at the bottom of the spray chamber in Figure 10.42.

Electrothermal Atomizers

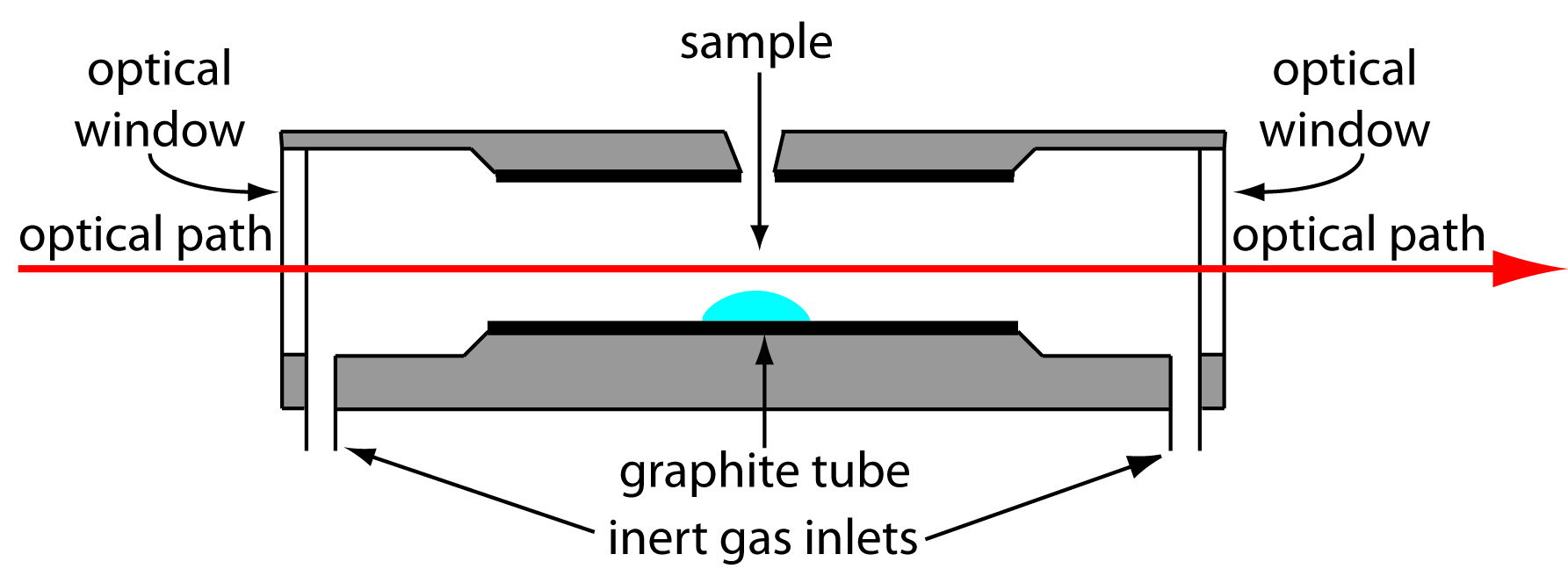
A significant improvement in sensitivity is achieved by using the resistive heating of a graphite tube in place of a flame. A typical electrothermal atomizer, also known as a graphite furnace, consists of a cylindrical graphite tube approximately 1–3 cm in length and 3–8 mm in diameter. As shown in Figure 10.45, the graphite tube is housed in an sealed assembly that has optically transparent windows at each end. A continuous stream of an inert gas is passed through the furnace, protecting the graphite tube from oxidation and removing the gaseous products produced during atomization. A power supply is used to pass a current through the graphite tube, resulting in resistive heating.

Figure 10.45: Diagram showing a cross-section of an electrothermal analyzer.

Samples of between 5–50 μL are injected into the graphite tube through a small hole at the top of the tube. Atomization is achieved in three stages. In the first stage the sample is dried to a solid residue using a current that raises the temperature of the graphite tube to about 110^oC. In the second stage, which is called ashing, the temperature is increased to between 350–1200^oC. At these temperatures any organic material in the sample is converted to CO₂ and H₂O, and volatile inorganic materials are vaporized. These gases are removed by the inert gas flow. In the final stage the sample is atomized by rapidly increasing the temperature to between 2000–3000^oC. The result is a transient absorbance peak whose height or area is proportional to the absolute amount of analyte injected into the graphite tube. Together, the three stages take approximately 45–90 s, with most of this time used for drying and ashing the sample.

Electrothermal atomization provides a significant improvement in sensitivity by trapping the gaseous analyte in the small volume within the graphite tube. The analyte’s concentration in the resulting vapor phase may be as much as 1000× greater than in a flame atomization.¹⁵ This improvement in sensitivity—and the resulting improvement in detection limits—is offset by a significant decrease in precision. Atomization efficiency is strongly influenced by the sample’s contact with the graphite tube, which is difficult to control reproducibly.

Miscellaneous Atomization Methods

A few elements may be atomized by a chemical reaction that produces a volatile product. Elements such as As, Se, Sb, Bi, Ge, Sn, Te, and Pb, for example, form volatile hydrides when reacted with NaBH₄ in acid. An inert gas carries the volatile hydrides to either a flame or to a heated quartz observation tube situated in the optical path. Mercury is determined by the cold-vapor method in which it is reduced to elemental mercury with SnCl₂. The volatile Hg is carried by an inert gas to an unheated observation tube situated in the instrument’s optical path.

10.4.2 Quantitative Applications

Atomic absorption is widely used for the analysis of trace metals in a variety of sample matrices. Using Zn as an example, atomic absorption methods have been developed for its determination in samples as diverse as water and wastewater, air, blood, urine, muscle tissue, hair, milk, breakfast cereals, shampoos, alloys, industrial plating baths, gasoline, oil, sediments, and rocks.

Developing a quantitative atomic absorption method requires several considerations, including choosing a method of atomization, selecting the wavelength and slit width, preparing the sample for analysis, minimizing spectral and chemical interferences, and selecting a method of standardization. Each of these topics is considered in this section.

Developing a Quantitative Method

Flame or Electrothermal Atomization? The most important factor in choosing a method of atomization is the analyte’s concentration. Because of its greater sensitivity, it takes less analyte to achieve a given absorbance when using electrothermal atomization. Table 10.10, which compares the amount of analyte needed to achieve an absorbance of 0.20 when using flame atomization and electrothermal atomization, is useful when selecting an atomization method. For example, flame atomization is the method of choice if our samples contain 1–10 mg Zn²⁺/L, but electrothermal atomization is the best choice for samples containing 1–10 μg Zn²⁺/L.

Table 10.10: Concentration of Analyte Yielding an Absorbance of 0.20

	Concentration (mg/L)^a
element	flame atomization	electrothermal atomization
Ag	1.5	0.0035
Al	40	0.015
As	40^b	0.050
Ca	0.8	0.003
Cd	0.6	0.001
Co	2.5	0.021
Cr	2.5	0.0075
Cu	1.5	0.012
Fe	2.5	0.006
Hg	70^b	0.52
Mg	0.15	0.00075
Mn	1	0.003
Na	0.3	0.00023
Ni	2	0.024
Pb	5	0.080
Pt	70	0.29
Sn	50^b	0.023
Zn	0.3	0.00071

^a Source: Varian Cookbook, SpectraAA Software Version 4.00 Pro.
^b As: 10 mg/L by hydride vaporization; Hg: 11.5 mg/L by cold-vapor; and Sn:18 mg/L by hydride vaporization

Selecting the Wavelength and Slit Width. The source for atomic absorption is a hollow cathode lamp consisting of a cathode and anode enclosed within a glass tube filled with a low pressure of Ne or Ar (Figure 10.46). Applying a potential across the electrodes ionizes the filler gas. The positively charged gas ions collide with the negatively charged cathode, sputtering atoms from the cathode’s surface. Some of the sputtered atoms are in the excited state and emit radiation characteristic of the metal(s) from which the cathode was manufactured. By fashioning the cathode from the metallic analyte, a hollow cathode lamp provides emission lines that correspond to the analyte’s absorption spectrum.

Note

Because atomic absorption lines are narrow, we need to use a line source instead of a continuum source (compare, for example, Figure 10.18 with Figure 10.20). The effective bandwidth when using a continuum source is roughly 1000× larger than an atomic absorption line; thus, P_T ≈ P₀, %T ≈ 100, and A ≈ 0. Because a hollow cathode lamp is a line source, P_T and P₀ have different values giving a %T < 100 and A > 0.

Figure 10.46: Photo of a typical multielemental hollow cathode lamp. The cathode in this lamp is fashioned from an alloy containing Co, Cr, Cu, Fe, Mn, and Ni, and is surrounded by a glass shield to isolate it from the anode. The lamp is filled with Ne gas. Also shown is the process leading to atomic emission. See the text for an explanation.

Each element in a hollow cathode lamp provides several atomic emission lines that we can use for atomic absorption. Usually the wavelength that provides the best sensitivity is the one we choose to use, although a less sensitive wavelength may be more appropriate for a larger concentration of analyte. For the Cr hollow cathode lamp in Table 10.11, for example, the best sensitivity is obtained using a wavelength of 357.9 nm.

Another consideration is the intensity of the emission line. If several emission lines meet our need for sensitivity, we may wish to use the emission line with the largest relative P₀ because there is less uncertainty in measuring P₀ and P_T. When analyzing samples containing ≈10 mg Cr/L, for example, the first three wavelengths in Table 10.11 provide an appropriate sensitivity. The wavelengths of 425.5 nm and 429.0 nm, however, have a greater P₀ and will provide less uncertainty in the measured absorbance.

Table 10.11 Atomic Emission Lines for a Cr Hollow Cathode Lamp

wavelength (nm)	slit width (nm)	mg Cr/L giving A = 0.20	P0 (relative)
357.9	0.2	2.5	40
425.4	0.2	12	85
429.0	0.5	20	100
520.5	0.2	1500	15
520.8	0.2	500	20

The emission spectrum from a hollow cathode lamp includes, besides emission lines for the analyte, additional emission lines for impurities present in the metallic cathode and from the filler gas. These additional lines are a source of stray radiation that leads to an instrumental deviation from Beer’s law. The monochromator’s slit width is set as wide as possible, improving the throughput of radiation, while, at the same time, being narrow enough to eliminate the stray radiation.

Preparing the Sample. Flame and electrothermal atomization require that the sample be in solution. Solid samples are brought into solution by dissolving in an appropriate solvent. If the sample is not soluble it may be digested, either on a hot-plate or by microwave, using HNO₃, H₂SO₄, or HClO₄. Alternatively, we can extract the analyte using a Soxhlet extractor. Liquid samples may be analyzed directly or extracted if the matrix is incompatible with the method of atomization. A serum sample, for instance, is difficult to aspirate when using flame atomization and may produce an unacceptably high background absorbance when using electrothermal atomization. A liquid–liquid extraction using an organic solvent and a chelating agent is frequently used to concentrate analytes. Dilute solutions of Cd²⁺, Co²⁺, Cu²⁺, Fe³⁺, Pb²⁺, Ni²⁺, and Zn²⁺, for example, can be concentrated by extracting with a solution of ammonium pyrrolidine dithiocarbamate in methyl isobutyl ketone.See Chapter 7 to review different methods for preparing samples for analysis.

Minimizing Spectral Interference. A spectral interference occurs when an analyte’s absorption line overlaps with an interferent’s absorption line or band. Because they are so narrow, the overlap of two atomic absorption lines is seldom a problem. On the other hand, a molecule’s broad absorption band or the scattering of source radiation is a potentially serious spectral interference.

An important consideration when using a flame as an atomization source is its effect on the measured absorbance. Among the products of combustion are molecular species that exhibit broad absorption bands and particulates that scatter radiation from the source. If we fail to compensate for these spectral interference, then the intensity of transmitted radiation decreases. The result is an apparent increase in the sample’s absorbance. Fortunately, absorption and scattering of radiation by the flame are corrected by analyzing a blank.

Spectral interferences also occur when components of the sample’s matrix other than the analyte react to form molecular species, such as oxides and hydroxides. The resulting absorption and scattering constitutes the sample’s background and may present a significant problem, particularly at wavelengths below 300 nm where the scattering of radiation becomes more important. If we know the composition of the sample’s matrix, then we can prepare our samples using an identical matrix. In this case the background absorption is the same for both the samples and standards. Alternatively, if the background is due to a known matrix component, then we can add that component in excess to all samples and standards so that the contribution of the naturally occurring interferent is insignificant. Finally, many interferences due to the sample’s matrix can be eliminated by increasing the atomization temperature. For example, by switching to a higher temperature flame it may be possible to prevent the formation of interfering oxides and hydroxides.

If the identity of the matrix interference is unknown, or if it is not possible to adjust the flame or furnace conditions to eliminate the interference, then we must find another method to compensate for the background interference. Several methods have been developed to compensate for matrix interferences, and most atomic absorption spectrophotometers include one or more of these methods.

One of the most common methods for background correction is to use a continuum source, such as a D₂ lamp. Because a D₂ lamp is a continuum source, absorbance of its radiation by the analyte’s narrow absorption line is negligible. Only the background, therefore, absorbs radiation from the D₂ lamp. Both the analyte and the background, on the other hand, absorb the hollow cathode’s radiation. Subtracting the absorbance for the D₂ lamp from that for the hollow cathode lamp gives a corrected absorbance that compensates for the background interference. Although this method of background correction may be quite effective, it does assume that the background absorbance is constant over the range of wavelengths passed by the monochromator. If this is not true, subtracting the two absorbances may underestimate or overestimate the background.

Note

Other methods of background correction have been developed, including Zeeman effect background correction and Smith–Hieftje background correction, both of which are included in some commercially available atomic absorption spectrophotometers. Consult the chapter’s additional resources for additional information.

Minimizing Chemical Interferences. The quantitative analysis of some elements is complicated by chemical interferences occurring during atomization. The two most common chemical interferences are the formation of nonvolatile compounds containing the analyte and ionization of the analyte.

One example of the formation of nonvolatile compounds is the effect of PO₄^3– or Al³⁺ on the flame atomic absorption analysis of Ca²⁺. In one study, for example, adding 100 ppm Al³⁺ to a solution of 5 ppm Ca²⁺ decreased the calcium ion’s absorbance from 0.50 to 0.14, while adding 500 ppm PO₄^3– to a similar solution of Ca²⁺ decreased the absorbance from 0.50 to 0.38. These interferences were attributed to the formation of nonvolatile particles of Ca₃(PO₄)₂ and an Al–Ca–O oxide.¹⁶

When using flame atomization, we can minimize the formation of nonvolatile compounds by increasing the flame’s temperature, either by changing the fuel-to-oxidant ratio or by switching to a different combination of fuel and oxidant. Another approach is to add a releasing agent or a protecting agent to the samples. A releasing agent is a species that reacts with the interferent, releasing the analyte during atomization. Adding Sr²⁺ or La³⁺ to solutions of Ca²⁺, for example, minimizes the effect of PO₄^3– and Al³⁺ by reacting in place of the analyte. Thus, adding 2000 ppm SrCl₂ to the Ca²⁺/PO₄^3– and Ca²⁺/Al³⁺ mixtures described in the previous paragraph increased the absorbance to 0.48. A protecting agent reacts with the analyte to form a stable volatile complex. Adding 1% w/w EDTA to the Ca²⁺/PO₄^3– solution described in the previous paragraph increased the absorbance to 0.52.

Ionization interferences occur when thermal energy from the flame or the electrothermal atomizer is sufficient to ionize the analyte

\[\ce{M}_{(g)} \overset{\Delta}{\rightleftharpoons} \ce{M}^+_{(g)} + e^− \tag{10.24}\]

where M is the analyte. Because the absorption spectra for M and M⁺ are different, the position of the equilibrium in reaction 10.24 affects absorbance at wavelengths where M absorbs. To limit ionization we add a high concentration of an ionization suppressor, which is simply a species that ionizes more easily than the analyte. If the concentration of the ionization suppressor is sufficient, then the increased concentration of electrons in the flame pushes reaction 10.24 to the left, preventing the analyte’s ionization. Potassium and cesium are frequently used as an ionization suppressor because of their low ionization energy.

Standardizing the Method. Because Beer’s law also applies to atomic absorption, we might expect atomic absorption calibration curves to be linear. In practice, however, most atomic absorption calibration curves are nonlinear, or linear for only a limited range of concentrations. Nonlinearity in atomic absorption is a consequence of instrumental limitations, including stray radiation from the hollow cathode lamp and the variation in molar absorptivity across the absorption line. Accurate quantitative work, therefore, often requires a suitable means for computing the calibration curve from a set of standards.

Note

Most instruments include several different algorithms for computing the calibration curve. The instrument in my lab, for example, includes five algorithms. Three of the algorithms fit absorbance data using linear, quadratic, or cubic polynomial functions of the analyte’s concentration. It also includes two algorithms that fit the concentrations of the standards to quadratic functions of the absorbance.

When possible, a quantitative analysis is best conducted using external standards. Unfortunately, matrix interferences are a frequent problem, particularly when using electrothermal atomization. For this reason the method of standard additions is often used. One limitation to this method of standardization, however, is the requirement that there be a linear relationship between absorbance and concentration.

Note

The best way to appreciate the theoretical and practical details discussed in this section is to carefully examine a typical analytical method. Although each method is unique, the following description of the determination of Cu and Zn in biological tissues provides an instructive example of a typical procedure. The description here is based on Bhattacharya, S. K.; Goodwin, T. G.; Crawford, A. J. Anal. Lett. 1984, 17, 1567–1593, and Crawford, A. J.; Bhattacharya, S. K. Varian Instruments at Work, Number AA–46, April 1985.

Representative Method 10.2

Determination of Cu and Zn in Tissue Samples

Description of Method

Copper and zinc are isolated from tissue samples by digesting the sample with HNO₃ after first removing any fatty tissue. The concentration of copper and zinc in the supernatant are determined by atomic absorption using an air-acetylene flame.

Procedure

Tissue samples are obtained by a muscle needle biopsy and dried for 24–30 h at 105^oC to remove all traces of moisture. The fatty tissue in the dried samples is removed by extracting overnight with anhydrous ether. After removing the ether, the sample is dried to obtain the fat-free dry tissue weight (FFDT). The sample is digested at 68^oC for 20–24 h using 3 mL of 0.75 M HNO₃. After centrifuging at 2500 rpm for 10 minutes, the supernatant is transferred to a 5-mL volumetric flask. The digestion is repeated two more times, for 2–4 hours each, using 0.9-mL aliquots of 0.75 M HNO₃. These supernatants are added to the 5-mL volumetric flask, which is diluted to volume with 0.75 M HNO₃. The concentrations of Cu and Zn in the diluted supernatant are determined by flame atomic absorption spectroscopy using an air-acetylene flame and external standards. Copper is analyzed at a wavelength of 324.8 nm with a slit width of 0.5 nm, and zinc is analyzed at 213.9 nm with a slit width of 1.0 nm. Background correction using a D₂ lamp is necessary for zinc. Results are reported as mg of Cu or Zn per gram of FFDT.

Questions

1. Describe the appropriate matrix for the external standards and for the blank?

The matrix for the standards and the blank should match the matrix of the samples; thus, an appropriate matrix is 0.75 M HNO₃. Any interferences from other components of the sample matrix are minimized by background correction.

2. Why is a background correction necessary for the analysis of Zn, but not for the analysis of Cu?

Background correction compensates for background absorption and scattering due to interferents in the sample. Such interferences are most severe when using a wavelength less than 300 nm. This is the case for Zn, but not for Cu.

3. A Cu hollow cathode lamp has several emission lines. Explain why this method uses the line at 324.8 nm.

wavelength (nm)	slit width (nm)	mg Cu/L for A = 0.20	P0 (relative)
217.9	0.2	15	3
218.2	0.2	15	3
222.6	0.2	60	5
244.2	0.2	400	15
249.2	0.5	200	24
324.8	0.5	1.5	100
327.4	0.5	3	87

With 1.5 mg Cu/L giving an absorbance of 0.20, the emission line at 324.8 nm has the best sensitivity. In addition, it is the most intense emission line, which decreases the uncertainty in the measured absorbance.

Example 10.10

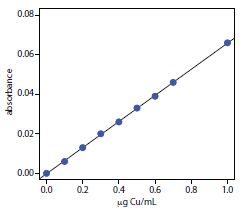
To evaluate the method described in Representative Method 10.2, a series of external standard is prepared and analyzed, providing the results shown here.¹⁷

μg Cu/mL	absorbance	μg Cu/mL	absorbance
0.000 0.100 0.200 0.300 0.400	0.000 0.006 0.013 0.020 0.026	0.500 0.600 0.700 1.000	0.033 0.039 0.046 0.066

A bovine liver standard reference material was used to evaluate the method’s accuracy. After drying and extracting the sample, a 11.23-mg FFDT tissue sample gives an absorbance of 0.023. Report the amount of copper in the sample as μg Cu/g FFDT.

Solution

Linear regression of absorbance versus the concentration of Cu in the standards gives a calibration curve with the following equation.

\[A = \mathrm{−0.0002 + 0.0661 × \dfrac{g\: Cu}{mL}}\]

Substituting the sample’s absorbance into the calibration equation gives the concentration of copper as 0.351 μg/mL. The concentration of copper in the tissue sample, therefore, is

\[\mathrm{\dfrac{\dfrac{0.351\: g\: Cu}{mL} × 5.000\: mL}{0.01123\: g\: sample} = 156\: g\: Cu/g\: FFDT}\]

10.4.3 - Evaluation of Atomic Absorption Spectroscopy

Scale of Operation

Atomic absorption spectroscopy is ideally suited for the analysis of trace and ultratrace analytes, particularly when using electrothermal atomization. For minor and major analyte, sample can be diluted before the analysis. Most analyses use a macro or a meso sample. The small volume requirement for electrothermal atomization or flame microsampling, however, makes practical the analysis micro and ultramicro samples.

Note

See Figure 3.5 to review the meaning of macro and meso for describing samples, and the meaning of major, minor, and ultratrace for describing analytes.

Accuracy

If spectral and chemical interferences are minimized, an accuracy of 0.5–5% is routinely attainable. When the calibration curve is nonlinear, accuracy may be improved by using a pair of standards whose absorbances closely bracket the sample’s absorbance and assuming that the change in absorbance is linear over this limited concentration range. Determinate errors for electrothermal atomization are often greater than that obtained with flame atomization due to more serious matrix interferences.

Precision

For absorbance values greater than 0.1–0.2, the relative standard deviation for atomic absorption is 0.3–1% for flame atomization and 1–5% for electrothermal atomization. The principle limitation is the variation in the concentration of free analyte atoms resulting from variations in the rate of aspiration, nebulization, and atomization when using a flame atomizer, and the consistency of injecting samples when using electrothermal atomization.

Sensitivity

The sensitivity of a flame atomic absorption analysis is influenced strongly by the flame’s composition and by the position in the flame from which we monitor the absorbance. Normally the sensitivity of an analysis is optimized by aspirating a standard solution of the analyte and adjusting operating conditions, such as the fuel-to-oxidant ratio, the nebulizer flow rate, and the height of the burner, to give the greatest absorbance. With electrothermal atomization, sensitivity is influenced by the drying and ashing stages that precede atomization. The temperature and time used for each stage must be optimized for each type of sample.

Note

See Chapter 14 for several strategies for optimizing experiments.

Sensitivity is also influenced by the sample’s matrix. We have already noted, for example, that sensitivity can be decreased by chemical interferences. An increase in sensitivity may be realized by adding a low molecular weight alcohol, ester, or ketone to the solution, or by using an organic solvent.

Selectivity

Due to the narrow width of absorption lines, atomic absorption provides excellent selectivity. Atomic absorption can be used for the analysis of over 60 elements at concentrations at or below the level of μg/L.

Time, Cost, and Equipment

The analysis time when using flame atomization is short, with sample throughputs of 250–350 determinations per hour when using a fully automated system. Electrothermal atomization requires substantially more time per analysis, with maximum sample throughputs of 20–30 determinations per hour. The cost of a new instrument ranges from between $10,000–$50,000 for flame atomization, and from $18,000–$70,000 for electrothermal atomization. The more expensive instruments in each price range include double-beam optics, automatic samplers, and can be programmed for multielemental analysis by allowing the wavelength and hollow cathode lamp to be changed automatically.

Contributors

David Harvey (DePauw University)