3.4: Selecting an Analytical Method
- Page ID
- 5764
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A method is the application of a technique to a specific analyte in a specific matrix. We can develop an analytical method for determining the concentration of lead in drinking water using any of the techniques mentioned in the previous section. A gravimetric method, for example, might precipitate the lead as \(\ce{PbSO_4}\) or \(\ce{PbCrO_4}\), and use the precipitate’s mass as the analytical signal. Lead forms several soluble complexes, which we can use to design a complexation titrimetric method. As shown in Figure 3.2.1, we can use graphite furnace atomic absorption spectroscopy to determine the concentration of lead in drinking water. Finally, the availability of multiple oxidation states (\(\ce{Pb^0}\), \(\ce{Pb^{2+}}\), \(\ce{Pb^{4+}}\)) makes electrochemical methods feasible.
The requirements of the analysis determine the best method. In choosing a method, consideration is given to some or all the following design criteria: accuracy, precision, sensitivity, selectivity, robustness, ruggedness, scale of operation, analysis time, availability of equipment, and cost.
Accuracy
Accuracy is how closely the result of an experiment agrees with the “true” or expected result. We can express accuracy as an absolute error, e
\[e = \mathrm{obtained\: result - expected\: result}\]
or as a percentage relative error, \(\%\ce{e_{r}}\)
\[\%e_\ce{r} = \mathrm{\dfrac{obtained\: result - expected\: result}{expected\: result} × 100}\]
A method’s accuracy depends on many things, including the signal’s source, the value of \(\ce{k_{A}}\) in Equation 3.3.1 or Equation 3.3.2, and the ease of handling samples without loss or contamination. In general, methods relying on total analysis techniques, such as gravimetry and titrimetry, produce results of higher accuracy because we can measure mass and volume with high accuracy, and because the value of \(\ce{k_{A}}\) is known exactly through stoichiometry.
Since it is unlikely that we know the true result, we use an expected or accepted result when evaluating accuracy. For example, we might use a reference standard, which has an accepted value, to establish an analytical method’s accuracy. You will find a more detailed treatment of accuracy in Chapter 4, including a discussion of sources of errors.
Precision
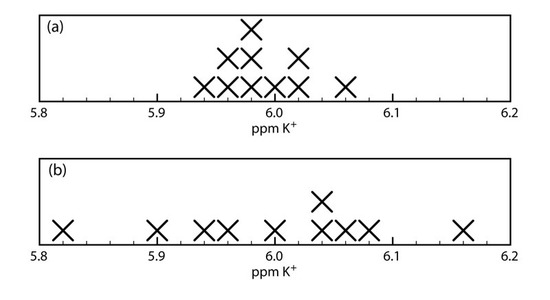
When a sample is analyzed several times, the individual results are rarely the same. Instead, the results are randomly scattered. Precision is a measure of this variability. The closer the agreement between individual analyses, the more precise the results. For example, in determining the concentration of \(\ce{K^+}\) in serum the results shown in Figure \(\PageIndex{1a}\) are more precise than those in Figure \(\PageIndex{1b}\). It is important to understand that precision does not imply accuracy. That the data in Figure \(\PageIndex{1a}\) are more precise does not mean that the first set of results is more accurate. In fact, neither set of results may be accurate.
Figure \(\PageIndex{1}\):Two determinations of the concentration of \(\ce{K^+}\) in serum, showing the effect of precision on the distribution of individual results. The data in (a) are less scattered and, therefore, more precise than the data in (b).
A method’s precision depends on several factors, including the uncertainty in measuring the signal and the ease of handling samples reproducibly. In most cases we can measure the signal for a total analysis method with a higher precision than the corresponding signal for a concentration method. Precision is covered in more detail in Chapter 4.
Confusing accuracy and precision is a common mistake. See Ryder, J.; Clark, A. U. Chem. Ed. 2002, 6, 1–3, and Tomlinson, J.; Dyson, P. J.; Garratt, J. U. Chem. Ed. 2001, 5, 16–23 for discussions of this and other common misconceptions about the meaning of error. You will find a more detailed treatment of precision in Chapter 4, including a discussion of sources of errors.
Sensitivity
The ability to demonstrate that two samples have different amounts of analyte is an essential part of many analyses. A method’s sensitivity is a measure of its ability to establish that such differences are significant. Sensitivity is often confused with a method’s detection limit, which is the smallest amount of analyte that we can determine with confidence.
Confidence, as we will see in Chapter 4, is a statistical concept that builds on the idea of a population of results. For this reason, we will postpone our discussion of detection limits to Chapter 4. For now, the definition of a detection limit given here is sufficient.
Sensitivity is equivalent to the proportionality constant, \(\ce{k_{A}}\), in Equations 3.3.1 and 3.3.2. If \(\ce{\Delta S_{A}}\) is the smallest difference that we can measure between two signals, then the smallest detectable difference in the absolute amount or relative amount of analyte is
\[\Delta n_\ce{A} = \dfrac{\Delta S_\ce{A}}{k_\ce{A}} \hspace{20px} \ce{or} \hspace{20px} \Delta C_\ce{A} = \dfrac{\Delta S_\ce{A}}{k_\ce{A}}\]
Suppose, for example, that our analytical signal is a measurement of mass using a balance whose smallest detectable increment is ±0.0001 g. If our method’s sensitivity is 0.200, then our method can conceivably detect a difference in mass of as little as
\[\mathrm{\Delta \mathit{n}_A = \dfrac{±0.0001\: g}{0.200} = ±0.0005\: g}\]
For two methods with the same \(\ce{∆S_{A}}\), the method with the greater sensitivity—the larger \(\ce{k_{A}}\)—is better able to discriminate between smaller amounts of analyte.
Specificity and Selectivity
An analytical method is specific if its signal depends only on the analyte. Although specificity is the ideal, few analytical methods are completely free from the influence of interfering species. When an interferent contributes to the signal, we expand Equations 3.3.1 and 3.3.2 to include its contribution to the sample’s signal, \(\ce{S_{samp}}\)
\[S_\ce{samp} = S_\ce{A} + S_\ce{I} = k_\ce{A}n_\ce{A} + k_\ce{I}n_\ce{I}\label{3.3}\]
\[S_\ce{samp} = S_\ce{A} + S_\ce{I} = k_\ce{A}C_\ce{A} + k_\ce{I}C_\ce{I}\label{3.4}\]
where \(\ce{S_{I}}\) is the interferent’s contribution to the signal, \(\ce{k_{I}}\) is the interferent’s sensitivity, and \(\ce{n_{I}}\) and \(\ce{C_{I}}\) are the moles (or grams) and concentration of the interferent in the sample.
Selectivity is a measure of a method’s freedom from interferences. The selectivity of a method for the interferent relative to the analyte is defined by a selectivity coefficient, \(\ce{K_{A,I}}\)
\[K_\textrm{A,I} = \dfrac{k_\ce{I}}{k_\ce{A}}\label{3.5}\]
which may be positive or negative depending on the sign of \(\ce{k_{I}}\) and \(\ce{k_{A}}\). The selectivity coefficient is greater than +1 or less than –1 when the method is more selective for the interferent than for the analyte.
Although \(\ce{k_{A}}\) and \(\ce{k_{I}}\) are usually positive, they also may be negative. For example, some analytical methods work by measuring the concentration of a species that reacts with the analyte. As the analyte’s concentration increases, the concentration of the species producing the signal decreases, and the signal becomes smaller. If the signal in the absence of analyte is assigned a value of zero, then the subsequent signals are negative.
Determining the selectivity coefficient’s value is easy if we already know the values for \(\ce{k_{A}}\) and \(\ce{k_{I}}\). As shown by Example \(\PageIndex{1}\), we also can determine \(\ce{K_{A,I}}\) by measuring Ssamp in the presence of and in the absence of the interferent.
Example \(\PageIndex{1}\)
A method for the analysis of \(\ce{Ca^{2+}}\) in water suffers from an interference in the presence of \(\ce{Zn^{2+}}\). When the concentration of \(\ce{Ca^{2+}}\) is 100 times greater than that of \(\ce{Zn^{2+}}\) the analysis for \(\ce{Ca^{2+}}\) gives a relative error of +0.5%. What is the selectivity coefficient for this method?
Solution
Since only relative concentrations are reported, we can arbitrarily assign absolute concentrations. To make the calculations easy, we will let \(\ce{C_{Ca} = 100}\) (arbitrary units) and \(\ce{C_{Zn} = 1}\). A relative error of +0.5% means that the signal in the presence of \(\ce{Zn^{2+}}\) is 0.5% greater than the signal in the absence of zinc. Again, we can assign values to make the calculation easier. If the signal in the absence of zinc is 100 (arbitrary units), then the signal in the presence of zinc is 100.5.
The value of \(\ce{k_{Ca}}\) is determined using Equation 3.3.2
\[k_\ce{Ca} = \dfrac{S_\ce{Ca}}{C_\ce{Ca}} = \dfrac{100}{100} = 1\]
In the presence of zinc the signal is given by Equation \(\ref{3.4}\); thus
\[S_\ce{samp} = 100.5 = k_\ce{Ca}C_\ce{Ca}+ k_\ce{Zn}C_\ce{Zn} = (1×100) + k_\ce{Zn}× 1\]
Solving for \(\ce{k_{Zn}}\) gives a value of 0.5. The selectivity coefficient is
\[K_\textrm{Ca,Zn} =\dfrac{k_\ce{Zn}}{k_\ce{Ca}} = \dfrac{0.5}{1} = 0.5\]
Exercise \(\PageIndex{1}\)
Wang and colleagues describe a fluorescence method for the analysis of \(\ce{Ag^+}\) in water. When analyzing a solution containing 1.0 × 10-9 M \(\ce{Ag^{+}}\) and 1.1× 10-7 M \(\ce{Ni^{2+}}\) the fluorescence intensity (the signal) was +4.9% greater than that obtained for a sample of 1.0 × 10-9 M \(\ce{Ag^{+}}\). What is \(\ce{K_{Ag,Ni}}\) for this analytical method? The full citation for the data in this exercise is Wang, L.; Liang, A. N.; Chen, H.; Liu, Y.; Qian, B.; Fu, J. Anal. Chim. Acta 2008, 616, 170-176.
Click here to review your answer to this exercise.
The selectivity coefficient provides us with a useful way to evaluate an interferent’s potential effect on an analysis. Solving Equation \(\ref{3.5}\) for \(\ce{k_{I}}\)
\[k_\ce{I}=K_\textrm{A,I}×k_\ce{A}\label{3.6}\]
substituting in Equation \(\ref{3.3}\) and Equation \(\ref{3.4}\), and simplifying gives
\[S_\ce{samp} = k_\ce{A} \left \{n_\ce{A} + K_\textrm{A,I} × n_\ce{I}\right \}\label{3.7}\]
\[S_\ce{samp} = k_\ce{A} \left\{C_\ce{A} + K_\textrm{A,I} × C_\ce{I}\right\}\label{3.8}\]
An interferent will not pose a problem as long as the term \(\ce{K_{A,I} × n_{I}}\) in Equation \(\ref{3.7}\) is significantly smaller than \(\ce{n_{A}}\), or if \(\ce{K_{A,I} × C_{I}}\) in Equation \(\ref{3.8}\) is significantly smaller than \(\ce{C_{A}}\).
Example \(\PageIndex{2}\)
Barnett and colleagues developed a method for determining the concentration of codeine in poppy plants. As part of their study they determined the method’s response to codeine in the presence of several interferents. For example, the authors found that the method’s signal for 6-methoxycodeine was 6 (arbitrary units) when that for an equimolar solution of codeine was 40.
Figure \(\PageIndex{2}\): Codein
- What is the value of the selectivity coefficient when 6-methoxycodeine is the interferent and codeine is the analyte.
- If the concentration of codeine must be known with an accuracy of ±0.50%, what is the maximum relative concentration of 6-methoxycodeine (i.e. [6-methoxycodeine]/[codeine]) that can be present?
Solution
- The signals due to the analyte, \(\ce{S_{A}}\), and the interferent, \(\ce{S_{I}}\), are
\[S_\ce{A} =k_\ce{A}C_\ce{A} \hspace{20px} S_\ce{I} =k_\ce{I}C_\ce{I}\]
Solving these equations for \(\ce{k_{A}}\) and \(\ce{k_{I}}\), and substituting into Equation \(\ref{3.6}\) gives
\[K_\textrm{A,I} = \dfrac{S_\ce{I} / C_\ce{I}}{S_\ce{A} / C_\ce{A}}\]
Since the concentrations of analyte and interferent are equimolar (\(\ce{C_{A} = C_{I}}\)), we have
\[K_\textrm{A,I} = \dfrac{S_\ce{I}}{S_\ce{A}} = \dfrac{6}{40} = 0.15\]
- To achieve an accuracy of better than ±0.50% the term \(\ce{K_{A,I} × C_{I}}\) in Equation \(\ref{3.8}\) must be less than 0.50% of \(\ce{C_{A}}\); thus
\[K_\textrm{A,I}×C_\ce{I} ≤ 0.0050 × C_\ce{A}\]
Solving this inequality for the ratio \(\ce{C_{I}/C_{A}}\) and substituting in the value for \(\ce{K_{A,I}}\) from part (a) gives
\[\dfrac{C_\ce{I}}{C_\ce{A}} ≤ \dfrac{0.0050}{K_\textrm{A,I}} = \dfrac{0.0050}{0.15} = 0.033\]
Therefore, the concentration of 6-methoxycodeine can not exceed 3.3% of codeine’s concentration.
Exercise \(\PageIndex{2}\)
Mercury (II) also is an interferent in the fluorescence method for \(\ce{Ag^+}\) developed by Wang and colleagues (see Exercise \(\PageIndex{1}\) for the citation). The selectivity coefficient, \(\ce{K_{Ag,Hg}}\) has a value of -1.0 × 10-3.
- What is the significance of the selectivity coefficient’s negative sign?
- Suppose you plan to use this method to analyze solutions with concentrations of \(\ce{Ag^+}\) that are no smaller than 1.0 nM. What is the maximum concentration of \(\ce{Hg^{2+}}\) you can tolerate to ensure that your percentage relative errors are less than ±1.0%?
Click here to review your answers to this exercise.
When a method’s signal is the result of a chemical reaction—for example, when the signal is the mass of a precipitate—there is a good chance that the method is not very selective and that it is susceptible to interferences. Problems with selectivity also are more likely when the analyte is present at a very low concentration.7
Look back at Figure 1.1.1, which shows Fresenius’ analytical method for the determination of nickel in ores. The reason there are so many steps in this procedure is that precipitation reactions generally are not very selective. The method in Figure 1.1.2 includes fewer steps because dimethylglyoxime is a more selective reagent. Even so, if an ore contains palladium, additional steps will be needed to prevent the palladium from interfering.
Robustness and Ruggedness
For a method to be useful it must provide reliable results. Unfortunately, methods are subject to a variety of chemical and physical interferences that contribute uncertainty to the analysis. When a method is relatively free from chemical interferences, we can use it on many analytes in a wide variety of sample matrices. Such methods are considered robust.
Random variations in experimental conditions also introduces uncertainty. If a method’s sensitivity, \(\ce{k}\), is too dependent on experimental conditions, such as temperature, acidity, or reaction time, then a slight change in any of these conditions may give a significantly different result. A rugged method is relatively insensitive to changes in experimental conditions.
Scale of Operation
Another way to narrow the choice of methods is to consider three potential limitations: the amount of sample available for the analysis, the expected concentration of analyte in the samples, and the minimum amount of analyte that produces a measurable signal. Collectively, these limitations define the analytical method’s scale of operations.
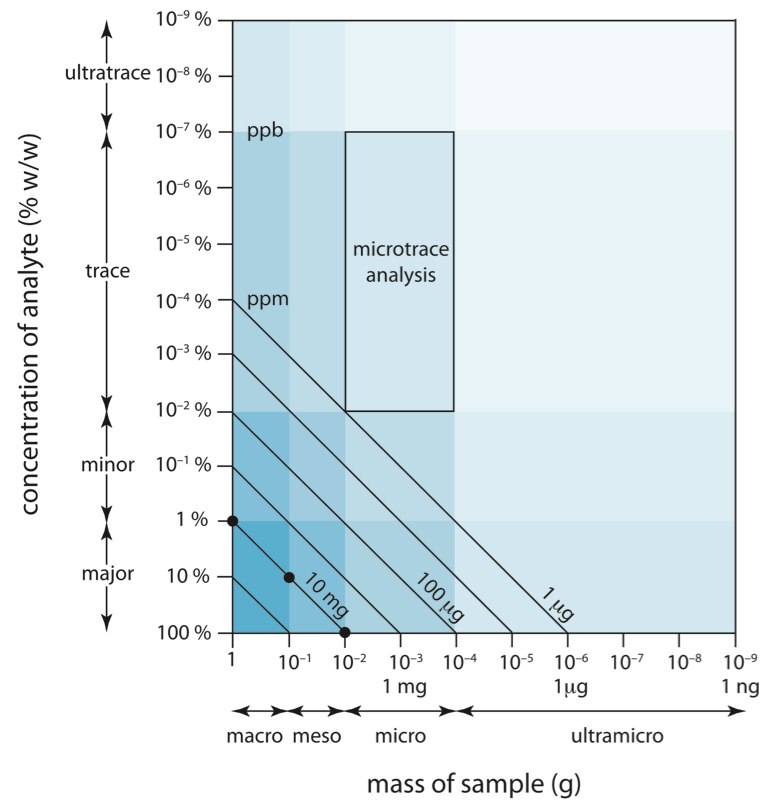
We can display the scale of operations graphically (Figure \(\PageIndex{3}\)) by plotting the sample’s size on the x-axis and the analyte’s concentration on the y-axis. For convenience, we divide samples into macro (>0.1 g), meso (10 mg–100 mg), micro (0.1 mg–10 mg), and ultramicro (<0.1 mg) sizes, and we divide analytes into major (>1% w/w), minor (0.01% w/w–1% w/w), trace (10-7% w/w–0.01% w/w), and ultratrace (<10‑7% w/w) components. The analyte’s concentration and the sample’s size provide a characteristic description for an analysis. For example, in a microtrace analysis the sample weighs between 0.1 mg–10 mg and contains a concentration of analyte between 10–2% w/w–10–7% w/w.
Diagonal lines connecting the axes show combinations of sample size and analyte concentration containing the same mass of analyte. As shown in Figure \(\PageIndex{3}\), for example, a 1-g sample that is 1% w/w analyte has the same amount of analyte (10 mg) as a 100-mg sample that is 10% w/w analyte, or a 10-mg sample that is 100% w/w analyte.
Figure \(\PageIndex{3}\): Scale of operations for analytical methods (adapted from references 8a and 8b). The shaded areas define different types of analyses. The boxed area, for example, represents a microtrace analysis. The diagonal lines show combinations of sample size and analyte concentration containing the same mass of analyte. The three filled circles (•), for example, indicate analyses using 10 mg of analyte.
We can use Figure \(\PageIndex{3}\) to establish limits for analytical methods. If a method’s minimum detectable signal is equivalent to 10 mg of analyte, then it is best suited to a major analyte in a macro or meso sample. Extending the method to an analyte with a concentration of 0.1% w/w requires a sample of 10 g, which is rarely practical due to the complications of carrying such a large amount of material through the analysis. On the other hand, small samples containing trace amounts of analyte place significant restrictions on an analysis. For example, 1-mg sample with an analyte present at 10–4% w/w contains just 1 ng of analyte. If we can isolate the analyte in 1 mL of solution, then we need an analytical method that can reliably detect it at a concentration of 1 ng/mL.
It should not surprise you to learn that total analysis methods typically require macro or meso samples containing major analytes. Concentration methods are particularly useful for minor, trace, and ultratrace analytes in macro, meso, and micro samples.
Equipment, Time, and Cost
Finally, we can compare analytical methods with respect to equipment needs, the time to complete an analysis, and the cost per sample. Methods relying on instrumentation are equipment-intensive and may require significant operator training. For example, the graphite furnace atomic absorption spectroscopic method for determining lead in water requires a significant capital investment in the instrument and an experienced operator to obtain reliable results. Other methods, such as titrimetry, require less expensive equipment and less training.
The time to complete an analysis for one sample is often fairly similar from method to method. This is somewhat misleading, however, because much of this time is spent preparing solutions and gathering together equipment. Once the solutions and equipment are in place, the sampling rate may differ substantially from method to method. Additionally, some methods are more easily automated. This is a significant factor in selecting a method for a laboratory that handles a high volume of samples.
The cost of an analysis depends on many factors, including the cost of equipment and reagents, the cost of hiring analysts, and the number of samples that can be processed per hour. In general, methods relying on instruments cost more per sample then other methods.
Making the Final Choice
Unfortunately, the design criteria discussed in this section are not mutually independent.9 Working with smaller samples or improving selectivity often comes at the expense of precision. Minimizing cost and analysis time may decrease accuracy. Selecting a method requires carefully balancing the design criteria. Usually, the most important design criterion is accuracy, and the best method is the one giving the most accurate result. When the need for results is urgent, as is often the case in clinical labs, analysis time may become the critical factor.
In some cases it is the sample’s properties that determine the best method. A sample with a complex matrix, for example, may require a method with excellent selectivity to avoid interferences. Samples in which the analyte is present at a trace or ultratrace concentration usually require a concentration method. If the quantity of sample is limited, then the method must not require a large amount of sample.
Determining the concentration of lead in drinking water requires a method that can detect lead at the parts per billion concentration level. Selectivity is important because other metal ions are present at significantly higher concentrations. A method using graphite furnace atomic absorption spectroscopy is a common choice for determining lead in drinking water because it meets these specifications. The same method is also useful for determining lead in blood where its ability to detect low concentrations of lead using a few microliters of sample are important considerations.