4.E: Exercises

14.1: Factors that Affect Reaction Rates

Q14.1.1

What information can you obtain by studying the chemical kinetics of a reaction? Does a balanced chemical equation provide the same information? Why or why not?

S14.1.1

Kinetics gives information on the reaction rate and reaction mechanism; the balanced chemical equation gives only the stoichiometry of the reaction.

Q14.1.2

If you were tasked with determining whether to proceed with a particular reaction in an industrial facility, why would studying the chemical kinetics of the reaction be important to you?

S14.1.2

Studying chemical kinetics determines whether to proceed with a reaction as it measures the rate of a reaction. Reactions conducted in an industrial facility mix compounds together, heating and stirring them for a while, before moving to the next process. When the compounds are then moved to the next phase of the process it is important to know how long to hold the reaction at one stage before continuing, to make sure a reaction has finished before starting the next one

Q14.1.3

What is the relationship between each of the following factors and the reaction rate: reactant concentration, temperature of the reaction, physical properties of the reactants, physical and chemical properties of the solvent, and the presence of a catalyst?

S14.1.3

Reactant concentration:

Reaction rate and the concentration of reactants have a direct relationship; as concentration goes up, so does reaction rate. This is because a higher concentration causes the reactants to have a higher probability to collide with a another reactant particle, possibly inducing the chemical reaction. This comes from the Collision theory.

Reaction temperature:

Reaction rate and the reaction temperature also have a direct relationship; as temperature goes up, so does reaction rate. A higher temperature makes the particles move at a faster speed so when two or more reactant particles collide, they collide with more energy and are more likely to reach the activation energy threshold, starting a chemical reaction.

Physical properties of the reactants:

If the reactants have the same physical properties, they are more likely to react, increasing the reaction rate, because the reactants mix and are more likely to collide another one of the reactants.

Physical and chemical properties of the solvent:

The properties of the solvent also affect the rates of a reaction. High viscosity means that particles more slowly than in low viscosity solvents, so reaction rates are slower in high viscosity solvents than in low viscosity solvents. This indicates an inverse relationship between viscosity and reaction rate.

Presence of a catalyst:

The chemical definition of a catalyst in a substance that increases the rate of a reaction without being used up in the reaction. Therefore, if a catalyst is present, reaction rate increases.

Q14.1.4

A slurry is a mixture of a finely divided solid with a liquid in which it is only sparingly soluble. As you prepare a reaction, you notice that one of your reactants forms a slurry with the solvent, rather than a solution. What effect will this have on the reaction rate? What steps can you take to try to solve the problem?

Q14.1.5

Why does the reaction rate of virtually all reactions increase with an increase in temperature? If you were to make a glass of sweetened iced tea the old-fashioned way, by adding sugar and ice cubes to a glass of hot tea, which would you add first?

S14.1.5

Increasing the temperature increases the average kinetic energy of molecules and ions, causing them to collide more frequently and with greater energy, which increases the reaction rate. First dissolve sugar in the hot tea, and then add the ice.

Q14.1.6

In a typical laboratory setting, a reaction is carried out in a ventilated hood with air circulation provided by outside air. A student noticed that a reaction that gave a high yield of a product in the winter gave a low yield of that same product in the summer, even though his technique did not change and the reagents and concentrations used were identical. What is a plausible explanation for the different yields?

Q14.1.7

A very active area of chemical research involves the development of solubilized catalysts that are not made inactive during the reaction process. Such catalysts are expected to increase reaction rates significantly relative to the same reaction run in the presence of a heterogeneous catalyst. What is the reason for anticipating that the relative rate will increase?

Q14.1.8

Water has a dielectric constant more than two times greater than that of methanol (80.1 for H₂O and 33.0 for CH₃OH). Which would be your solvent of choice for a substitution reaction between an ionic compound and a polar reagent, both of which are soluble in either methanol or water? Why?

14.2: Reaction Rates

Q14.2.1

Explain why the reaction rate is generally fastest at early time intervals. For the second-order A + B → C, what would the plot of the concentration of C versus time look like during the course of the reaction?

S14.2.1

Reactant concentrations are highest at the beginning of a reaction. The plot of [C] versus t is a curve with a slope that becomes steadily less positive.

Q14.2.2

Explain the differences between a differential rate law and an integrated rate law. What two components do they have in common? Which form is preferred for obtaining a reaction order and a rate constant? Why?

Q14.2.3

Diffusion-controlled reactions have rates that are determined only by the reaction rate at which two reactant molecules can diffuse together. These reactions are rapid, with second-order rate constants typically on the order of 10¹⁰ L/(mol·s). Are the reactions expected to be faster or slower in solvents that have a low viscosity? Why? Consider the reactions H₃O⁺ + OH⁻ → 2H₂O and H₃O⁺ + N(CH₃)₃ → H₂O + HN(CH₃)₃⁺ in aqueous solution. Which would have the higher rate constant? Why?

S14.2.3

Faster in a less viscous solvent because the rate of diffusion is higher; the H₃O⁺/OH⁻ reaction is faster due to the decreased relative size of reactants and the higher electrostatic attraction between the reactants.

Q14.2.4

What information can be obtained from the reaction order? What correlation does the reaction order have with the stoichiometry of the overall equation?

Q14.2.5

During the hydrolysis reaction A + H₂O → B + C, the concentration of A decreases much more rapidly in a polar solvent than in a nonpolar solvent. How would this effect be reflected in the overall reaction order?

Q14.2.6

The reaction rate of a particular reaction in which A and B react to make C is as follows:

\(\textrm{rate}=-\dfrac{\Delta[\textrm A]}{\Delta t}=\dfrac{1}{2}\left ( \dfrac{\Delta[\textrm C]}{\Delta t} \right )\)

Write a reaction equation that is consistent with this rate law. What is the rate expression with respect to time if 2A are converted to 3C?

Q14.2.7

While commuting to work, a person drove for 12 min at 35 mph, then stopped at an intersection for 2 min, continued the commute at 50 mph for 28 min, drove slowly through traffic at 38 mph for 18 min, and then spent 1 min pulling into a parking space at 3 mph. What was the average rate of the commute? What was the instantaneous rate at 13 min? at 28 min?

Q14.2.8

Why do most studies of chemical reactions use the initial rates of reaction to generate a rate law? How is this initial rate determined? Given the following data, what is the reaction order? Estimate.

Time (s)	[A] (M)
120	0.158
240	0.089
360	0.062

Q14.2.9

Predict how the reaction rate will be affected by doubling the concentration of the first species in each equation.

1. C₂H₅I → C₂H₄ + HI: rate = k[C₂H₅I]
2. SO + O₂ → SO₂ + O: rate = k[SO][O₂]
3. 2CH₃ → C₂H₆: rate = k[CH₃]²
4. ClOO → Cl + O₂: rate = k

Q14.2.10

Cleavage of C₂H₆ to produce two CH₃· radicals is a gas-phase reaction that occurs at 700°C. This reaction is first order, with k = 5.46 × 10⁻⁴ s⁻¹. How long will it take for the reaction to go to 15% completion? to 50% completion?

S14.2.10

298 s; 1270 s

Q14.2.11

Three chemical processes occur at an altitude of approximately 100 km in Earth’s atmosphere.

\[\mathrm{N_2^+}+\mathrm{O_2}\xrightarrow{k_1}\mathrm{N_2}+\mathrm{O_2^+}\]

\[\mathrm{O_2^+}+\mathrm{O}\xrightarrow{k_2}\mathrm{O_2}+\mathrm{O^+}\]

\[(\mathrm{O^+}+\mathrm{N_2}\xrightarrow{k_3}\mathrm{NO^+}+\mathrm{N}\]

Write a rate law for each elementary reaction. If the rate law for the overall reaction were found to be rate = k[N₂⁺][O₂], which one of the steps is rate limiting?

Q14.2.12

The oxidation of aqueous iodide by arsenic acid to give I₃⁻ and arsenous acid proceeds via the following reaction:

\(\mathrm{H_3AsO_4(aq)}+\mathrm{3I^-(aq)}+\mathrm{2H^+(aq)}\overset{k_{\textrm f}}{\underset{k_{\textrm r}}{\rightleftharpoons}}\mathrm{H_3AsO_3(aq)}+\mathrm{I_3^-(aq)}+\mathrm{H_2O(l)}\)

Write an expression for the initial rate of decrease of [I₃⁻], Δ[I₃⁻]/Δt. When the reaction rate of the forward reaction is equal to that of the reverse reaction: k_f/k_r = [H₃AsO₃][I₃⁻]/[H₃AsO₄][I⁻]³[H⁺]². Based on this information, what can you say about the nature of the rate-determining steps for the reverse and the forward reactions?

14.3: Concentration and Rate

14.4: The Change of Concentration with Time

Q14.4.1

What are the characteristics of a zeroth-order reaction? Experimentally, how would you determine whether a reaction is zeroth order?

Q14.4.2

Predict whether the following reactions are zeroth order and explain your reasoning.

1. a substitution reaction of an alcohol with HCl to form an alkyl halide and water
2. catalytic hydrogenation of an alkene
3. hydrolysis of an alkyl halide to an alcohol
4. enzymatic conversion of nitrate to nitrite in a soil bacterium

Q14.4.3

In a first-order reaction, what is the advantage of using the integrated rate law expressed in natural logarithms over the rate law expressed in exponential form?

Q14.4.4

If the reaction rate is directly proportional to the concentration of a reactant, what does this tell you about (a) the reaction order with respect to the reactant and (b) the overall reaction order?

Q14.4.5

The reaction of NO with O₂ is found to be second order with respect to NO and first order with respect to O₂. What is the overall reaction order? What is the effect of doubling the concentration of each reagent on the reaction rate?

Q14.4.6

Iodide reduces Fe(III) according to the following reaction:

\[2Fe^{3+}(soln) + 2I^−(soln) → 2Fe^{2+}(soln) + I_2(soln)\]

Experimentally, it was found that doubling the concentration of Fe(III) doubled the reaction rate, and doubling the iodide concentration increased the reaction rate by a factor of 4. What is the reaction order with respect to each species? What is the overall rate law? What is the overall reaction order?

S14.4.6

First order in Fe³⁺; second order in I⁻; third order overall; rate = k[Fe³⁺][I⁻]².

Q14.4.7

Benzoyl peroxide is a medication used to treat acne. Its rate of thermal decomposition at several concentrations was determined experimentally, and the data were tabulated as follows:

Experiment	[Benzoyl Peroxide]0 (M)	Initial Rate (M/s)
1	1.00	2.22 × 10^−4
2	0.70	1.64 × 10^−4
3	0.50	1.12 × 10^−4
4	0.25	0.59 × 10^−4

What is the reaction order with respect to benzoyl peroxide? What is the rate law for this reaction?

S14.4.7

The general rate law is: rate = k [Benzoyl Peroxide]^m. In order to find the reaction order with respect to benzoyl peroxide, divide two rate laws and solve for m:

\(\dfrac{rate_2}{rate_1}=\dfrac{k_2}{k_1} \left ( \dfrac{[Benzoyl Peroxide]_2}{[Benzoyl Peroxide]_1} \right )^m\)

\(\dfrac{1.64 × 10^-4 \dfrac{M}{s}}{2.22 × 10^-4 \dfrac{M}{s}}=( \dfrac{0.070 M}{1.00 M})^m\)

\(0.738=(0.7)^m\)

\(m=0.85\)

rate law: rate = k [Benzoyl Peroxide]^0.85

Q14.4.8

1-Bromopropane is a colorless liquid that reacts with S₂O₃²⁻ according to the following reaction:

\[C_3H_7Br + S_2O_3^{2−} → C_3H_7S_2O_3^− + Br^−\]

The reaction is first order in 1-bromopropane and first order in S₂O₃²⁻, with a rate constant of 8.05 × 10⁻⁴ M⁻¹·s⁻¹. If you began a reaction with 40 mmol/100 mL of C₃H₇Br and an equivalent concentration of S₂O₃²⁻, what would the initial reaction rate be? If you were to decrease the concentration of each reactant to 20 mmol/100 mL, what would the initial reaction rate be?

S14.4.8

1.29 × 10⁻⁴ M/s; 3.22 × 10⁻⁵ M/s

Q14.4.9

The experimental rate law for the reaction 3A + 2B → C + D was found to be Δ[C]/Δt = k[A]²[B] for an overall reaction that is third order. Because graphical analysis is difficult beyond second-order reactions, explain the procedure for determining the rate law experimentally.

14.5: Temperature and Rate

Q14.5.1

Although an increase in temperature results in an increase in kinetic energy, this increase in kinetic energy is not sufficient to explain the relationship between temperature and reaction rates. How does the activation energy relate to the chemical kinetics of a reaction? Why does an increase in temperature increase the reaction rate despite the fact that the average kinetic energy is still less than the activation energy?

S14.5.1

Activation energy is required for a collision between molecules to result in a chemical reaction, as well it is related to the rate due to the Arrhenius equation

Activation energy is the threshold of energy needed in order for a reaction to occur. Reactant particles must collide with enough energy to be able to break chemical bonds, that will then allow the creation of new bonds. If the particles do not have enough energy, when they collide they will simply bounce off one another.

k=Ae^(-Ea/RT). The increase in temperature increases the rate of reaction despite the fact the average kinetic is less than the activation energy since it increase the rate of collision between molecules.

With an increase in temperature, there is a greater distribution of kinetic energy among reactant particles. This increase of temperature allows the rate in which particles collide with one another to increase. Although the average kinetic energy is still lower than the activation energy, the increase of collisions among particles increases the chance of particles that contain enough energy to overcome the energy barrier to collide. Thus, the reaction rate increases due to this increased rate of collisions.

Additionally, there is a higher amount of molecules that have sufficient kinetic energy to overcome the energy barrier, despite the average energy of all these molecules still being lower than the activation energy.

Q14.5.2

For any given reaction, what is the relationship between the activation energy and each of the following?

1. electrostatic repulsions
2. bond formation in the activated complex
3. the nature of the activated complex

S14.5.2

1.) Electrostatic repulsion: Electrostatic repulsion is the unfavorable interaction between two species of like charge. Activation energy is the minimum amount of energy needed for a reaction to occur. Reacting molecules must have enough energy to overcome electrostatic repulsion, and a minimum amount of energy is required to break chemical bonds so that new ones may be formed.

2.) Bond formation in the activated complex: An activated complex is an intermediate state that is formed during the conversion of reactants into products. Bond breaking can increase activation energy as breaking bonds requires energy.

3.) Nature of the activated complex: The activation energy of a chemical reaction is the difference between the energy of the activated complex and the energy of the reactants. If the structure has a high steric hindrance the activation energy will be higher.

Q14.5.3

If you are concerned with whether a reaction will occur rapidly, why would you be more interested in knowing the magnitude of the activation energy than the change in potential energy for the reaction?

Q14.5.4

The product C in the reaction A + B → C + D can be separated easily from the reaction mixture. You have been given pure A and pure B and are told to determine the activation energy for this reaction to determine whether the reaction is suitable for the industrial synthesis of C. How would you do this? Why do you need to know the magnitude of the activation energy to make a decision about feasibility?

Q14.5.5

Above E_a, molecules collide with enough energy to overcome the energy barrier for a reaction. Is it possible for a reaction to occur at a temperature less than that needed to reach E_a? Explain your answer.

Q14.5.6

What is the relationship between A, E_a, and T? How does an increase in A affect the reaction rate?

Q14.5.7

Of two highly exothermic reactions with different values of E_a, which would need to be monitored more carefully: the one with the smaller value or the one with the higher value? Why?

Q14.5.8

What happens to the approximate rate of a reaction when the temperature of the reaction is increased from 20°C to 30°C? What happens to the reaction rate when the temperature is raised to 70°C? For a given reaction at room temperature (20°C), what is the shape of a plot of reaction rate versus temperature as the temperature is increased to 70°C?

S14.5.8

The reaction rate will approximately double: 20°C to 30°C, the reaction rate increases by about 2¹ = 2; 20°C to 70°C, the reaction rate increases by about 2⁵ = 32-fold. A plot of reaction rate versus temperature will give an exponential increase: rate ∝ 2^ΔT/10.

Q14.5.9

Acetaldehyde, used in silvering mirrors and some perfumes, undergoes a second-order decomposition between 700 and 840 K. From the data in the following table, would you say that acetaldehyde follows the general rule that each 10 K increase in temperature doubles the reaction rate?

T (K)	k (M^−1·s^−1)
720	0.024
740	0.051
760	0.105
800	0.519

Q14.5.10

Bromoethane reacts with hydroxide ion in water to produce ethanol. The activation energy for this reaction is 90 kJ/mol. If the reaction rate is 3.6 × 10⁻⁵ M/s at 25°C, what would the reaction rate be at the following temperatures?

1. 15°C
2. 30°C
3. 45°C

Q14.5.11

An enzyme-catalyzed reaction has an activation energy of 15 kcal/mol. How would the value of the rate constant differ between 20°C and 30°C? If the enzyme reduced the \(E_a\) from 25 kcal/mol to 15 kcal/mol, by what factor has the enzyme increased the reaction rate at each temperature?

S14.5.11

1. 1.0 × 10⁻⁵ M/s
2. 6.6 × 10⁻⁵ M/s
3. 3.5 × 10⁻⁴ M/s

Q14.5.12

The data in the following table are the rate constants as a function of temperature for the dimerization of 1,3-butadiene. What is the activation energy for this reaction?

T (K)	k (M^−1·min^−1)
529	1.4
560	3.7
600	25
645	82

S14.5.12

100 kJ/mol

Q14.5.13

The reaction rate at 25°C is 1.0 × 10⁻⁴ M/s. Increasing the temperature to 75°C causes the reaction rate to increase to 7.0 × 10⁻² M/s. Estimate \(E_a\) for this process. If \(E_a\) were 25 kJ/mol and the reaction rate at 25°C is 1.0 × 10⁻⁴ M/s, what would be the reaction rate at 75°C?

14.6: Reaction Mechanisms

Q14.6.1

How does the term molecularity relate to elementary reactions? How does it relate to the overall balanced chemical equation?

Q14.6.2

What is the relationship between the reaction order and the molecularity of a reaction? What is the relationship between the reaction order and the balanced chemical equation?

Q14.6.3

When you determine the rate law for a given reaction, why is it valid to assume that the concentration of an intermediate does not change with time during the course of the reaction?

Q14.6.3

If you know the rate law for an overall reaction, how would you determine which elementary reaction is rate determining? If an intermediate is contained in the rate-determining step, how can the experimentally determined rate law for the reaction be derived from this step?

Q14.6.4

Give the rate-determining step for each case.

1. Traffic is backed up on a highway because two lanes merge into one.
2. Gas flows from a pressurized cylinder fitted with a gas regulator and then is bubbled through a solution.
3. A document containing text and graphics is downloaded from the Internet.

Q14.6.5

Before being sent on an assignment, an aging James Bond was sent off to a health farm where part of the program’s focus was to purge his body of radicals. Why was this goal considered important to his health?

S14.6.5

Free radicals are uncharged molecules with an unpaired valence electron. The reason these are so dangerous is because they like to grab electrons from other atoms to fill their own outer shell. This allows them to impair protein function because free radicals readily oxidize proteins and cell membrane which could lead to a loss of function. It was important to purge James Bond of radicals because radicals set off chain reactions of continuously pulling electrons from molecules, which in turn, can damage cells in the body.

Q14.6.6

Cyclopropane, a mild anesthetic, rearranges to propylene via a collision that produces and destroys an energized species. The important steps in this rearrangement are as follows:

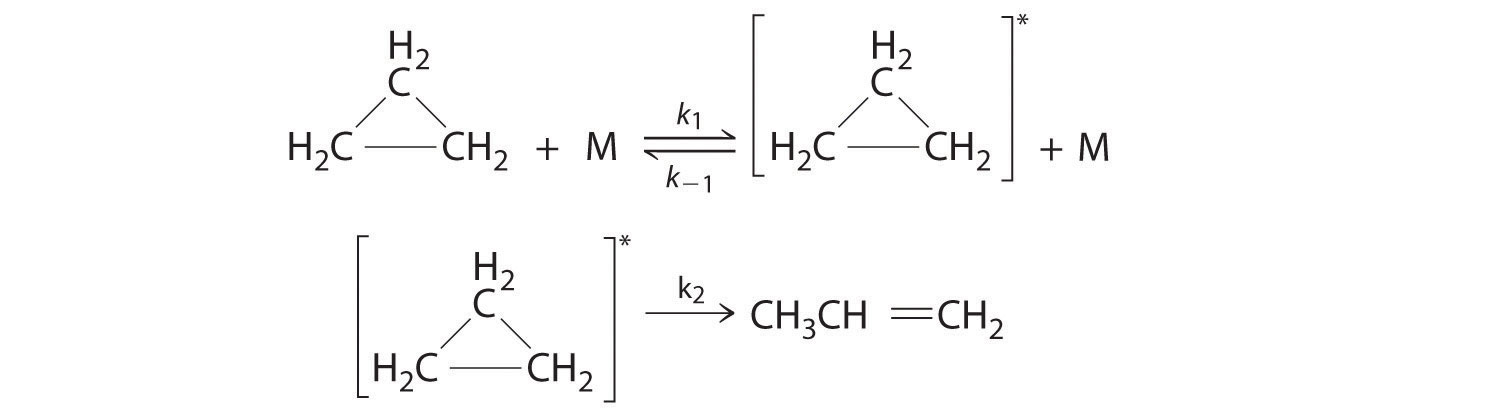
where M is any molecule, including cyclopropane. Only those cyclopropane molecules with sufficient energy (denoted with an asterisk) can rearrange to propylene. Which step determines the rate constant of the overall reaction?

S14.6.6

When we are trying to decide which step is a rate-determining step, you have to look at which step is the slowest of them all, since we have no knowledge of the time scale for either of these steps we have to look elsewhere to determine the rate-determining step.

In our specific problem, we do not know what exact molecules we have however we do see that the first step is an equilibrium since it has a double-headed arrow with two k values one that is the reciprocal of the other. Since it is an equilibrium we can reasonably assume that energized propane is rapidly created which would lead us to the conclusion that the second step is the slower of the two steps and is, therefore, the rate-determining step. So, the second step (with k₂) determines the rate constant of the overall reaction.

Q14.6.7

Above approximately 500 K, the reaction between NO₂ and CO to produce CO₂ and NO follows the second-order rate law Δ[CO₂]/Δt = k[NO₂][CO]. At lower temperatures, however, the rate law is Δ[CO₂]/Δt = k′[NO₂]², for which it is known that NO₃ is an intermediate in the mechanism. Propose a complete low-temperature mechanism for the reaction based on this rate law. Which step is the slowest?

S14.6.7

Given that NO₃ is an intermediate in the low temperature reaction mechanism, we automatically know two things: 1) NO₃ won't show up in the final overall reaction, and thus, 2) NO₃ will be in the products of the first reaction of the mechanism and in the reactants of the second reaction. We can also assume that since we're given an intermediate from the problem, this is the only intermediate (so we won't have to dream up any other compounds that might exist in the series of reactions.) These things being said, the lower temperature reaction mechanism will look like this:

\[2NO_2(g) \rightarrow NO_3(g) + NO(g) \tag{1}\]

\[CO(g) + NO_3(g) \rightarrow CO_2(g) + NO_2(g) \tag{2}\]

And the overall reaction will look like this (notice how NO₃ is not present):

\[CO(g) + NO_2(g) \rightarrow CO_2(g) + NO(g) \tag{overall reaction}\]

Now that we have the reaction mechanism written out, we can go about determining which step is the slowest. It would be pretty tricky to do this if we weren't given any further information, however, we know two more things: 1) the high-temperature mechanism's rate = k[NO₂][CO] meaning that it took place in one step (given that the overall reaction is also equal to this rate) and 2) the low-temperature mechanism's rate = k′[NO₂]². These two things being said, we've both confirmed that our proposed low-temperature reaction mechanism is in fact two steps, and that we have a means to find which step is slower.

By using the "guess-and-check" method we can label each step reaction one at a time as the "slow reaction" and see if the rate matches up with the rate given to us.

Let's first try the 2nd reaction. (see above)

By using rate laws we can determine that the rate of the reaction must be in terms of its reactants, which follows:

\[\textrm{k}\textrm{[CO][NO}_3\textrm{]}\]

... But wait! We can't have the overall reaction rate in terms of an intermediate.

By looking at the 1st reaction, we can determine that we can sub in "[NO₂] /[NO]" for "[NO₃]" since by writing the full reaction rate of the first step and solving for [NO₃] this is equivalent. So, we now have the overall rate of the mechanism as the following given the 2nd reaction is the "slow reaction:"

\[\textrm{k}\dfrac{\textrm{[CO][NO}_2\textrm{]}^2}{\textrm{[NO}\textrm{]}}\]

Note that NO₂ is raised to the second power to account for the stoichiometry of the balanced reaction.

So clearly the 2nd reaction isn't the slow reaction since the rate is not equivalent to what we were given!

Let's check the rate of the 1st reaction now...

\[\textrm{k}\textrm{[NO}_2\textrm{]}^2\]

What do you know... the rates are equal!

We have now confirmed that the 1st reaction is the slow reaction equation, since its rate is equivalent to the overall reaction rate.

Q14.6.8

Nitramide (O₂NNH₂) decomposes in aqueous solution to N₂O and H₂O. What is the experimental rate law (Δ[N₂O]/Δt) for the decomposition of nitramide if the mechanism for the decomposition is as follows?

\(\mathrm{O_2NNH_2}\overset{k_1}{\underset{k_{-1}}{\rightleftharpoons}}\mathrm{O_2NNH^-}+\mathrm{H^+}\)	\((\textrm{fast})\)
\(\mathrm{O_2NNH^-}\xrightarrow{k_2}\mathrm{N_2O}+\mathrm{OH^-}\)	\((\textrm{slow})\)
\(\mathrm{H^+}+\mathrm{OH^-}\xrightarrow{k_3}\mathrm{H_2O}\)	\((\textrm{fast})\)

Assume that the rates of the forward and reverse reactions in the first equation are equal.

S14.6.8

We know that the slowest step of the reaction is the rate determining step, since it usually has the highest activation energy requirement. As a result, the slowest step of the reaction is the experimental rate law we are looking for.

Note: since the slowest step is the rate determining step, that usually means there is some intermediate in between. Intermediates should NEVER be a part of the rate law mechanism.

$$rate = rate_2 = {k_2}{[O_2NNH^{-}]}$$

Since Nitramide is an intermediate, we must find some way to substitute it. To solve that problem, we look for where Nitramide is produced and consumed. We see that

\[rate_1 = {k_1}{[O_2NNH_2]}\]

\[rate_{-1} = {k_{-1}}{[O_2NNH^-]}{[H^+]}\]

Since these two rates produce and consume the same amount of \(O_2NNH^{-}\) over the same time period, we can set them equal to each other and solve for the intermediate

\[rate_1 = rate_{-1}\]

\[{k_1}{[O_2NNH_2]} = {k_{-1}}{[O_2NNH^-]}{[H^+]}\]

\[{[O_2NNH^-]} = \frac{k_1{[O_2NNH_2]}}{k_{-1}{[H^+]}}\]

Substituting this equation back into our original equation gives us

\[rate=rate_2=k_2\frac{k_1[O_2NNH_2]}{k_{-1}[H^+]}\]

With all of the rate constants (k), we can clean up our equation a little bit by saying

\[k = \frac{k_2{k_1}}{k_{-1}}\]

Leaving us with

\[rate = \frac{k[O_2NNH_2]}{[H^+]}\]

A14.6.8

\(\textrm{rate}=k_2\dfrac{k_1[\mathrm{O_2NNH_2}]}{k_{-1}[\mathrm{H^+}]}=k\dfrac{[\mathrm{O_2NNH_2}]}{[\mathrm{H^+}]}\)

Q14.6.9

The following reactions are given:

\[\mathrm{A+B}\overset{k_1}{\underset{k_{-1}}{\rightleftharpoons}}\mathrm{C+D}\]

\[\mathrm{D+E}\xrightarrow{k_2}\mathrm F\]

What is the relationship between the relative magnitudes of \(k_{−1}\) and \(k_2\) if these reactions have the following rate law?

\[\dfrac{Δ[F]}{Δt} = k\dfrac{[A][B][E]}{[C]}\]

How does the magnitude of \(k_1\) compare to that of \(k_2\)? Under what conditions would you expect the rate law to be

\[\dfrac{Δ[F]}{Δt} =k′[A][B]?\]

Assume that the rates of the forward and reverse reactions in the first equation are equal.

S14.6.9

First, because we have broken the equations down into elementary steps we can write the rate laws for each step.

Step1:

\[A+B\xrightarrow[]{k_{1}} C+D\]

\[rate=k_{1}[A][B]\]

Step 2:

\[C+D \xrightarrow[]{k_{-1}} A+B\]

\[rate=k_{-1}[C][D]\]

Step 3:

\[D+E \xrightarrow[]{k_{2}} F\]

\[rate=k_{2}[D][E]\]

If we add a these steps together we see that we get overall reaction

\[A+B+E \rightarrow C+F\]

we can see that [D] is an intermediate and \[k_{1}=k_{-1}\]_.

Since we are not told which steps are fast or slow we need to use Steady State Approximation.

If the second step is the slower step (k-₁>>k₂) then our rate determining step would be

\[rate=k_{2}[D][E]\]

Since we can only write rate laws in terms of products and reactants we have to rewrite this so that we are not including an intermediate.

Assume: rate of [D] formation = rate of its disappearance

\[k_{1}[A][B]=k_{-1}[C][D]+k_{2}[D][E]\]

\[k_{1}[A][B]=[D](k_{-1}[C]+k_{2}[E])\]

Solving for [D] we find that

\[[D]= \frac{k_{1}[A][B]}{(k_{-1}[C]+k_{2}[E])}\]

now we can use this to substitute the intermediate [D] in the rate law to get an appropriate rate law.

\[rate=\frac{k_{2} k_{1}[A][B][E]}{(k_{-1}[C]+k_{2}[E])}\]

because we had already established k-₁>>k₂ we can assume that

\[k_{-1}[C]+k_{2}[E]\approx k_{-1}[C]\]

this would give us the observed rate law

\[\frac{\Delta [F]}{\Delta t}=\frac{k_{2}k_{1}[A][B][E]}{k_{-1}[C]}\]

to make this clearer we can set

\[k=\frac{(k_{2})(k_{1})}{(k_{-1})}\]

and we can then simplify it down to

\[\dfrac{Δ[F]}{Δt} = k\dfrac{[A][B][E]}{[C]}\]

we can see that all of these rate constants are related by this ratio k₂k₁/k-_1. Since k₂ is our rate determining step k-₁>>k₂ and since k₁=k-₁ then we can see that k₁>>k_2.

We would expect the rate law to be

\[\dfrac{Δ[F]}{Δt} =k′[A][B]?\]

if the rate determining step aka the slowest step is that corresponding to (step 1) since the rate law for this step is k₁[A][B] and this is the exact the same as the rate law that we were given.

14.7: Catalysis

Q14.7.1

What effect does a catalyst have on the activation energy of a reaction? What effect does it have on the frequency factor (A)? What effect does it have on the change in potential energy for the reaction?

S14.7.1

A catalyst lowers the activation energy of a reaction. Some catalysts can also orient the reactants and thereby increase the frequency factor. Catalysts have no effect on the change in potential energy for a reaction.

Q14.7.2

How is it possible to affect the product distribution of a reaction by using a catalyst?

Q14.7.3

A heterogeneous catalyst works by interacting with a reactant in a process called adsorption. What occurs during this process? Explain how this can lower the activation energy.

S14.7.3

In adsorption, a reactant binds tightly to a surface. Because intermolecular interactions between the surface and the reactant weaken or break bonds in the reactant, its reactivity is increased, and the activation energy for a reaction is often decreased.

Q14.7.4

What effect does increasing the surface area of a heterogeneous catalyst have on a reaction? Does increasing the surface area affect the activation energy? Explain your answer.

Q14.7.5

Identify the differences between a heterogeneous catalyst and a homogeneous catalyst in terms of the following.

1. ease of recovery
2. collision frequency
3. temperature sensitivity
4. cost

S14.7.4

1. Heterogeneous catalysts are easier to recover.
2. Collision frequency is greater for homogeneous catalysts.
3. Homogeneous catalysts are often more sensitive to temperature.
4. Homogeneous catalysts are often more expensive.

Q14.7.6

An area of intensive chemical research involves the development of homogeneous catalysts, even though homogeneous catalysts generally have a number of operational difficulties. Propose one or two reasons why a homogenous catalyst may be preferred.

S14.7.6

Catalysts are compounds that, when added to chemical reactions, reduce the activation energy and increase the reaction rate. The amount of a catalyst does not change during a reaction, as it is not consumed as part of the reaction process. Catalysts lower the energy required to reach the transition state of the reaction, allowing more molecular interactions to achieve that state. However, catalysts do not affect the degree to which a reaction progresses. In other words, though catalysts affect reaction kinetics, the equilibrium state remains unaffected.

Catalysts can be classified into two types: homogenous and heterogeneous. Homogenous catalysts are those which exist in the same phase (gas or liquid) as the reactants, while heterogeneous catalysts are not in the same phase as the reactants. Typically, heterogeneous catalysis involves the use of solid catalysts placed in a liquid reaction mixture. For this question, we will be discussing homogenous catalysts.

Most of the times, homogeneous catalysis involves the introduction of an aqueous phase catalyst into an aqueous solution of reactants. One reason why homogeneous catalysts are preferred over heterogeneous catalysts because homogeneous catalysts mix well in chemical reactions in comparison to heterogeneous catalysts. However, homogeneous catalyst is often irrecoverable after the reaction has run to completion.

Q14.7.7

Consider the following reaction between cerium(IV) and thallium(I) ions:

\[\ce{2Ce^{4+} + Tl^+ → 2Ce^{3+} + Tl^{3+}}\]

This reaction is slow, but Mn²⁺ catalyzes it, as shown in the following mechanism:

\[\ce{Ce^{4+} + Mn^{2+} → Ce^{3+} + Mn^{3+}}\]

\[\ce{Ce^{4+} + Mn^{3+} → Ce^{3+} + Mn^{4+}}\]

\[\ce{Mn^{4+} + Tl^{+ }→ Tl^{3+} + Mn^{2+}}\]

In what way does \(Mn^{2+}\) increase the reaction rate?

S14.7.7

The Mn²⁺ ion donates two electrons to Ce⁴⁺, one at a time, and then accepts two electrons from Tl⁺. Because Mn can exist in three oxidation states separated by one electron, it is able to couple one-electron and two-electron transfer reactions.

Q14.7.8

The text identifies several factors that limit the industrial applications of enzymes. Still, there is keen interest in understanding how enzymes work for designing catalysts for industrial applications. Why?

S14.7.8

Enzymes are expensive to make, denature and fail at certain temperatures, are not that stable in a solution, and are very specific to the reaction it was made for. However, scientists can use the observations from enzymes to create catalysts that are more effective in aiding the reaction and cost less to produce. Overall, catalysts still play a large part in lowering the activation energy for reactions. Creating new catalysts can help in the improvement of areas such as medical, ecological, and even commercial products.

Q14.7.9

Most enzymes have an optimal pH range; however, care must be taken when determining pH effects on enzyme activity. A decrease in activity could be due to the effects of changes in pH on groups at the catalytic center or to the effects on groups located elsewhere in the enzyme. Both examples are observed in chymotrypsin, a digestive enzyme that is a protease that hydrolyzes polypeptide chains. Explain how a change in pH could affect the catalytic activity due to (a) effects at the catalytic center and (b) effects elsewhere in the enzyme. (Hint: remember that enzymes are composed of functional amino acids.)

Q14.7.10

At some point during an enzymatic reaction, the concentration of the activated complex, called an enzyme–substrate complex (\(ES\)), and other intermediates involved in the reaction is nearly constant. When a single substrate is involved, the reaction can be represented by the following sequence of equations:

\[\text {enzyme (E) + substrate (S)} \rightleftharpoons \text{enzyme-substrate complex (ES)} \rightleftharpoons \text{enzyme (E) + product (P)}\]

This can also be shown as follows:

\[E + S \underset{k_{-1}}{\stackrel{k_1}{\rightleftharpoons}} ES \underset{k_{-2}}{\stackrel{k_{2}}{\rightleftharpoons}} E+P\]

Using molar concentrations and rate constants, write an expression for the rate of disappearance of the enzyme–substrate complex. Typically, enzyme concentrations are small, and substrate concentrations are high. If you were determining the rate law by varying the substrate concentrations under these conditions, what would be your apparent reaction order?

S14.7.10

\(\dfrac{Δ[ES]}{Δt}=−(k_2+k_{−1})[ES]+k_1[E][S]+k_{−2}[E][P] \approx 0\); zeroth order in substrate.

Q14.7.11

A particular reaction was found to proceed via the following mechanism:

• \(A + B → C + D\) (slow)
• \(2C → E\) (fast)
• \(E + A → B + F\) (fast)

What is the overall reaction? Is this reaction catalytic, and if so, what species is the catalyst? Identify the intermediates

Q14.7.12

A particular reaction has two accessible pathways (A and B), each of which favors conversion of X to a different product (Y and Z, respectively). Under uncatalyzed conditions pathway A is favored, but in the presence of a catalyst pathway B is favored. Pathway B is reversible, whereas pathway A is not. Which product is favored in the presence of a catalyst? without a catalyst? Draw a diagram illustrating what is occurring with and without the catalyst.

S14.7.12

In both cases, the product of pathway A is favored. All of the Z produced in the catalyzed reversible pathway B will eventually be converted to X as X is converted irreversibly to Y by pathway A.

Q14.7.13

The kinetics of an enzyme-catalyzed reaction can be analyzed by plotting the reaction rate versus the substrate concentration. This type of analysis is referred to as a Michaelis–Menten treatment. At low substrate concentrations, the plot shows behavior characteristic of first-order kinetics, but at very high substrate concentrations, the behavior shows zeroth-order kinetics. Explain this phenomenon.