14.3: Concentration and Rates (Differential Rate Laws)
- Page ID
- 25177
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To understand the meaning of the rate law.
The factors that affect the reaction rate of a chemical reaction, which may determine whether a desired product is formed. In this section, we will show you how to quantitatively determine the reaction rate.
Rate Laws
Typically, reaction rates decrease with time because reactant concentrations decrease as reactants are converted to products. Reaction rates generally increase when reactant concentrations are increased. This section examines mathematical expressions called rate laws, which describe the relationships between reactant rates and reactant concentrations. Rate laws are mathematical descriptions of experimentally verifiable data.
Rate laws may be written from either of two different but related perspectives. A differential rate law expresses the reaction rate in terms of changes in the concentration of one or more reactants (Δ[R]) over a specific time interval (Δt). In contrast, an integrated rate law describes the reaction rate in terms of the initial concentration ([R]0) and the measured concentration of one or more reactants ([R]) after a given amount of time (t); integrated rate laws are discussed in more detail later. The integrated rate law is derived by using calculus to integrate the differential rate law. Whether using a differential rate law or integrated rate law, always make sure that the rate law gives the proper units for the reaction rate, usually moles per liter per second (M/s).
Reaction Orders
For a reaction with the general equation:
\[aA + bB \rightarrow cC + dD \label{14.3.1} \]
the experimentally determined rate law usually has the following form:
\[\text{rate} = k[A]^m[B]^n \label{14.3.2} \]
The proportionality constant (k) is called the rate constant, and its value is characteristic of the reaction and the reaction conditions. A given reaction has a particular rate constant value under a given set of conditions, such as temperature, pressure, and solvent; varying the temperature or the solvent usually changes the value of the rate constant. The numerical value of k, however, does not change as the reaction progresses under a given set of conditions.
Under a given set of conditions, the value of the rate constant does not change as the reaction progresses.
The reaction rate thus depends on the rate constant for the given set of reaction conditions and the concentration of A and B raised to the powers m and n, respectively. The values of m and n are derived from experimental measurements of the changes in reactant concentrations over time and indicate the reaction order, the degree to which the reaction rate depends on the concentration of each reactant; m and n need not be integers. For example, Equation \(\ref{14.3.2}\) tells us that Equation \(\ref{14.3.1}\) is mth order in reactant A and nth order in reactant B. It is important to remember that n and m are not related to the stoichiometric coefficients a and b in the balanced chemical equation and must be determined experimentally. The overall reaction order is the sum of all the exponents in the rate law: m + n.
The orders of the reactions (e.g. n and m) are not related to the stoichiometric coefficients in the balanced chemical (e.g., a and b).
To illustrate how chemists interpret a differential rate law, consider the experimentally derived rate law for the hydrolysis of t-butyl bromide in 70% aqueous acetone.
This reaction produces t-butanol according to the following equation:
\[(CH_3)_3CBr_{(soln)} + H_2O_{(soln)} \rightarrow (CH_3)_3COH_{(soln)} + HBr_{(soln)} \label{14.3.3} \]
Combining the rate expression in Equation \(\ref{14.3.2}\) with the definition of average reaction rate
\[\textrm{rate}=-\dfrac{\Delta[\textrm A]}{\Delta t} \nonumber \]
gives a general expression for the differential rate law:
\[\textrm{rate}=-\dfrac{\Delta[\textrm A]}{\Delta t}=k[\textrm A]^m[\textrm B]^n \label{14.3.4} \]
Inserting the identities of the reactants into Equation \(\ref{14.3.4}\) gives the following expression for the differential rate law for the reaction:
\[\textrm{rate}=-\dfrac{\Delta[\mathrm{(CH_3)_3CBr}]}{\Delta t}=k[\mathrm{(CH_3)_3CBr}]^m[\mathrm{H_2O}]^n \label{14.3.5} \]
Experiments to determine the rate law for the hydrolysis of t-butyl bromide show that the reaction rate is directly proportional to the concentration of (CH3)3CBr but is independent of the concentration of water. Therefore, m and n in Equation \(\ref{14.3.4}\) are 1 and 0, respectively, and,
\[\text{rate} = k[(CH_3)_3CBr]^1[H_2O]^0 = k[(CH_3)_3CBr] \label{14.3.6} \]
Because the exponent for the reactant is 1, the reaction is first order in (CH3)3CBr. It is zeroth order in water because the exponent for [H2O] is 0. (Recall that anything raised to the zeroth power equals 1.) Thus, the overall reaction order is 1 + 0 = 1. The reaction orders state in practical terms that doubling the concentration of (CH3)3CBr doubles the reaction rate of the hydrolysis reaction, halving the concentration of (CH3)3CBr halves the reaction rate, and so on. Conversely, increasing or decreasing the concentration of water has no effect on the reaction rate. (Again, when working with rate laws, there is no simple correlation between the stoichiometry of the reaction and the rate law. The values of k, m, and n in the rate law must be determined experimentally.) Experimental data show that k has the value 5.15 × 10−4 s−1 at 25°C. The rate constant has units of reciprocal seconds (s−1) because the reaction rate is defined in units of concentration per unit time (M/s). The units of a rate constant depend on the rate law for a particular reaction.
Under conditions identical to those for the t-butyl bromide reaction, the experimentally derived differential rate law for the hydrolysis of methyl bromide (CH3Br) is as follows:
\[\textrm{rate}=-\dfrac{\Delta[\mathrm{CH_3Br}]}{\Delta t}=k'[\mathrm{CH_3Br}] \label{14.3.7} \]
This reaction also has an overall reaction order of 1, but the rate constant in Equation \(\ref{14.3.7}\) is approximately 106 times smaller than that for t-butyl bromide. Thus, methyl bromide hydrolyzes about 1 million times more slowly than t-butyl bromide, and this information tells chemists how the reactions differ on a molecular level.
Frequently, changes in reaction conditions also produce changes in a rate law. In fact, chemists often alter reaction conditions to study the mechanics of a reaction. For example, when t-butyl bromide is hydrolyzed in an aqueous acetone solution containing OH− ions rather than in aqueous acetone alone, the differential rate law for the hydrolysis reaction does not change. In contrast, for methyl bromide, the differential rate law becomes
\[\text{rate} =k″[CH_3Br][OH^−] \nonumber \]
with an overall reaction order of 2. Although the two reactions proceed similarly in neutral solution, they proceed very differently in the presence of a base, providing clues as to how the reactions differ on a molecular level.
An experiment shows that the reaction of nitrogen dioxide with carbon monoxide:
is second order in NO2 and zero order in CO at 100 °C. What is the rate law for the reaction?
Solution
The reaction will have the form:
\[\ce{rate}=k[\ce{NO2}]^m[\ce{CO}]^n \nonumber \]
The reaction is second order in NO2; thus m = 2. The reaction is zero order in CO; thus n = 0. The rate law is:
\[\ce{rate}=k[\ce{NO2}]^2[\ce{CO}]^0=k[\ce{NO2}]^2 \nonumber \]
Remember that a number raised to the zero power is equal to 1, thus [CO]0 = 1, which is why we can simply drop the concentration of CO from the rate equation: the rate of reaction is solely dependent on the concentration of NO2. When we consider rate mechanisms later in this chapter, we will explain how a reactant’s concentration can have no effect on a reaction despite being involved in the reaction.
The rate law for the reaction:
\[\ce{H2}(g)+\ce{2NO}(g)⟶\ce{N2O}(g)+\ce{H2O}(g) \nonumber \]
has been experimentally determined to be \(rate = k[NO]^2[H_2]\). What are the orders with respect to each reactant, and what is the overall order of the reaction?
- Answer
-
- order in NO = 2
- order in H2 = 1
- overall order = 3
In a transesterification reaction, a triglyceride reacts with an alcohol to form an ester and glycerol. Many students learn about the reaction between methanol (CH3OH) and ethyl acetate (CH3CH2OCOCH3) as a sample reaction before studying the chemical reactions that produce biodiesel:
\[\ce{CH3OH + CH3CH2OCOCH3 ⟶ CH3OCOCH3 + CH3CH2OH} \nonumber \]
The rate law for the reaction between methanol and ethyl acetate is, under certain conditions, experimentally determined to be:
\[\ce{rate}=k[\ce{CH3OH}] \nonumber \]
What is the order of reaction with respect to methanol and ethyl acetate, and what is the overall order of reaction?
- Answer
-
- order in CH3OH = 1
- order in CH3CH2OCOCH3 = 0
- overall order = 1
Below are three reactions and their experimentally determined differential rate laws. For each reaction, give the units of the rate constant, give the reaction order with respect to each reactant, give the overall reaction order, and predict what happens to the reaction rate when the concentration of the first species in each chemical equation is doubled.
- \[\mathrm{2HI(g)}\xrightarrow{\textrm{Pt}}\mathrm{H_2(g)}+\mathrm{I_2(g)} \\ \textrm{rate}=-\frac{1}{2}\left (\frac{\Delta[\mathrm{HI}]}{\Delta t} \right )=k[\textrm{HI}]^2 \nonumber \]
- \[\mathrm{2N_2O(g)}\xrightarrow{\Delta}\mathrm{2N_2(g)}+\mathrm{O_2(g)} \\ \textrm{rate}=-\frac{1}{2}\left (\frac{\Delta[\mathrm{N_2O}]}{\Delta t} \right )=k \nonumber \]
- \[\mathrm{cyclopropane(g)}\rightarrow\mathrm{propane(g)} \\ \textrm{rate}=-\frac{\Delta[\mathrm{cyclopropane}]}{\Delta t}=k[\mathrm{cyclopropane}] \nonumber \]
Given: balanced chemical equations and differential rate laws
Asked for: units of rate constant, reaction orders, and effect of doubling reactant concentration
Strategy:
- Express the reaction rate as moles per liter per second [mol/(L·s), or M/s]. Then determine the units of each chemical species in the rate law. Divide the units for the reaction rate by the units for all species in the rate law to obtain the units for the rate constant.
- Identify the exponent of each species in the rate law to determine the reaction order with respect to that species. Add all exponents to obtain the overall reaction order.
- Use the mathematical relationships as expressed in the rate law to determine the effect of doubling the concentration of a single species on the reaction rate.
Solution
- A [HI]2 will give units of (moles per liter)2. For the reaction rate to have units of moles per liter per second, the rate constant must have reciprocal units [1/(M·s)]:
\[k\textrm M^2=\dfrac{\textrm M}{\textrm s}k=\dfrac{\textrm{M/s}}{\textrm M^2}=\dfrac{1}{\mathrm{M\cdot s}}=\mathrm{M^{-1}\cdot s^{-1}} \nonumber \]
B The exponent in the rate law is 2, so the reaction is second order in HI. Because HI is the only reactant and the only species that appears in the rate law, the reaction is also second order overall.
C If the concentration of HI is doubled, the reaction rate will increase from k[HI]02 to k(2[HI])02 = 4k[HI]02. The reaction rate will therefore quadruple.
- A Because no concentration term appears in the rate law, the rate constant must have M/s units for the reaction rate to have M/s units.
B The rate law tells us that the reaction rate is constant and independent of the N2O concentration. That is, the reaction is zeroth order in N2O and zeroth order overall.
C Because the reaction rate is independent of the N2O concentration, doubling the concentration will have no effect on the reaction rate.
- A The rate law contains only one concentration term raised to the first power. Hence the rate constant must have units of reciprocal seconds (s−1) to have units of moles per liter per second for the reaction rate: M·s−1 = M/s.
B The only concentration in the rate law is that of cyclopropane, and its exponent is 1. This means that the reaction is first order in cyclopropane. Cyclopropane is the only species that appears in the rate law, so the reaction is also first order overall.
C Doubling the initial cyclopropane concentration will increase the reaction rate from k[cyclopropane]0 to 2k[cyclopropane]0. This doubles the reaction rate.
Given the following two reactions and their experimentally determined differential rate laws: determine the units of the rate constant if time is in seconds, determine the reaction order with respect to each reactant, give the overall reaction order, and predict what will happen to the reaction rate when the concentration of the first species in each equation is doubled.
- \(\begin{align}\textrm{CH}_3\textrm N\textrm{=NCH}_3\textrm{(g)}\rightarrow\mathrm{C_2H_6(g)}+\mathrm{N_2(g)}\hspace{5mm}&\textrm{rate}=-\frac{\Delta[\textrm{CH}_3\textrm N\textrm{=NCH}_3]}{\Delta t}
\\&=k[\textrm{CH}_3\textrm N\textrm{=NCH}_3]\end{align}\) - \(\begin{align}\mathrm{2NO_2(g)}+\mathrm{F_2(g)}\rightarrow\mathrm{2NO_2F(g)}\hspace{5mm}&\textrm{rate}=-\frac{\Delta[\mathrm{F_2}]}{\Delta t}=-\frac{1}{2}\left ( \frac{\Delta[\mathrm{NO_2}]}{\Delta t} \right )
\\&=k[\mathrm{NO_2}][\mathrm{F_2}]\end{align}\)
- Answer a
-
s−1; first order in CH3N=NCH3; first order overall; doubling [CH3N=NCH3] will double the reaction rate.
- Answer b
-
M−1·s−1; first order in NO2, first order in F2; second order overall; doubling [NO2] will double the reaction rate.
Determining the Rate Law of a Reaction
The number of fundamentally different mechanisms (sets of steps in a reaction) is actually rather small compared to the large number of chemical reactions that can occur. Thus understanding reaction mechanisms can simplify what might seem to be a confusing variety of chemical reactions. The first step in discovering the reaction mechanism is to determine the reaction’s rate law. This can be done by designing experiments that measure the concentration(s) of one or more reactants or products as a function of time. For the reaction \(A + B \rightarrow products\), for example, we need to determine k and the exponents m and n in the following equation:
\[\text{rate} = k[A]^m[B]^n \label{14.4.11} \]
To do this, we might keep the initial concentration of B constant while varying the initial concentration of A and calculating the initial reaction rate. This information would permit us to deduce the reaction order with respect to A. Similarly, we could determine the reaction order with respect to B by studying the initial reaction rate when the initial concentration of A is kept constant while the initial concentration of B is varied. In earlier examples, we determined the reaction order with respect to a given reactant by comparing the different rates obtained when only the concentration of the reactant in question was changed. An alternative way of determining reaction orders is to set up a proportion using the rate laws for two different experiments. Rate data for a hypothetical reaction of the type \(A + B \rightarrow products\) are given in Table \(\PageIndex{1}\).
| Experiment | [A] (M) | [B] (M) | Initial Rate (M/min) |
|---|---|---|---|
| 1 | 0.50 | 0.50 | 8.5 × 10−3 |
| 2 | 0.75 | 0.50 | 19 × 10−3 |
| 3 | 1.00 | 0.50 | 34 × 10−3 |
| 4 | 0.50 | 0.75 | 8.5 × 10−3 |
| 5 | 0.50 | 1.00 | 8.5 × 10−3 |
The general rate law for the reaction is given in Equation \(\ref{14.4.11}\). We can obtain m or n directly by using a proportion of the rate laws for two experiments in which the concentration of one reactant is the same, such as Experiments 1 and 3 in Table \(\PageIndex{3}\).
\[\dfrac{\mathrm{rate_1}}{\mathrm{rate_3}}=\dfrac{k[\textrm A_1]^m[\textrm B_1]^n}{k[\textrm A_3]^m[\textrm B_3]^n} \nonumber \]
Inserting the appropriate values from Table \(\PageIndex{3}\),
\[\dfrac{8.5\times10^{-3}\textrm{ M/min}}{34\times10^{-3}\textrm{ M/min}}=\dfrac{k[\textrm{0.50 M}]^m[\textrm{0.50 M}]^n}{k[\textrm{1.00 M}]^m[\textrm{0.50 M}]^n} \nonumber \]
Because 1.00 to any power is 1, [1.00 M]m = 1.00 M. We can cancel like terms to give 0.25 = [0.50]m, which can also be written as 1/4 = [1/2]m. Thus we can conclude that m = 2 and that the reaction is second order in A. By selecting two experiments in which the concentration of B is the same, we were able to solve for m.
Conversely, by selecting two experiments in which the concentration of A is the same (e.g., Experiments 5 and 1), we can solve for n.
\(\dfrac{\mathrm{rate_1}}{\mathrm{rate_5}}=\dfrac{k[\mathrm{A_1}]^m[\mathrm{B_1}]^n}{k[\mathrm{A_5}]^m[\mathrm{B_5}]^n}\)
Substituting the appropriate values from Table \(\PageIndex{3}\),
\[\dfrac{8.5\times10^{-3}\textrm{ M/min}}{8.5\times10^{-3}\textrm{ M/min}}=\dfrac{k[\textrm{0.50 M}]^m[\textrm{0.50 M}]^n}{k[\textrm{0.50 M}]^m[\textrm{1.00 M}]^n} \nonumber \]
Canceling leaves 1.0 = [0.50]n, which gives \(n = 0\); that is, the reaction is zeroth order in \(B\). The experimentally determined rate law is therefore
rate = k[A]2[B]0 = k[A]2
We can now calculate the rate constant by inserting the data from any row of Table \(\PageIndex{3}\) into the experimentally determined rate law and solving for \(k\). Using Experiment 2, we obtain
19 × 10−3 M/min = k(0.75 M)2
3.4 × 10−2 M−1·min−1 = k
You should verify that using data from any other row of Table \(\PageIndex{1}\) gives the same rate constant. This must be true as long as the experimental conditions, such as temperature and solvent, are the same.
Nitric oxide is produced in the body by several different enzymes and acts as a signal that controls blood pressure, long-term memory, and other critical functions. The major route for removing NO from biological fluids is via reaction with \(O_2\) to give \(NO_2\), which then reacts rapidly with water to give nitrous acid and nitric acid:
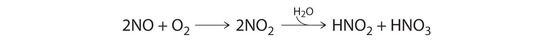
These reactions are important in maintaining steady levels of NO. The following table lists kinetics data for the reaction of NO with O2 at 25°C:
\[2NO(g) + O_2(g) \rightarrow 2NO_2(g) \nonumber \]
Determine the rate law for the reaction and calculate the rate constant.
| Experiment | [NO]0 (M) | [O2]0 (M) | Initial Rate (M/s) |
|---|---|---|---|
| 1 | 0.0235 | 0.0125 | 7.98 × 10−3 |
| 2 | 0.0235 | 0.0250 | 15.9 × 10−3 |
| 3 | 0.0470 | 0.0125 | 32.0 × 10−3 |
| 4 | 0.0470 | 0.0250 | 63.5 × 10−3 |
Given: balanced chemical equation, initial concentrations, and initial rates
Asked for: rate law and rate constant
Strategy:
- Compare the changes in initial concentrations with the corresponding changes in rates of reaction to determine the reaction order for each species. Write the rate law for the reaction.
- Using data from any experiment, substitute appropriate values into the rate law. Solve the rate equation for k.
Solution
A Comparing Experiments 1 and 2 shows that as [O2] is doubled at a constant value of [NO2], the reaction rate approximately doubles. Thus the reaction rate is proportional to [O2]1, so the reaction is first order in O2. Comparing Experiments 1 and 3 shows that the reaction rate essentially quadruples when [NO] is doubled and [O2] is held constant. That is, the reaction rate is proportional to [NO]2, which indicates that the reaction is second order in NO. Using these relationships, we can write the rate law for the reaction:
rate = k[NO]2[O2]
B The data in any row can be used to calculate the rate constant. Using Experiment 1, for example, gives
\[k=\dfrac{\textrm{rate}}{[\mathrm{NO}]^2[\mathrm{O_2}]}=\dfrac{7.98\times10^{-3}\textrm{ M/s}}{(0.0235\textrm{ M})^2(0.0125\textrm{ M})}=1.16\times10^3\;\mathrm{ M^{-2}\cdot s^{-1}} \nonumber \]
Alternatively, using Experiment 2 gives
\[k=\dfrac{\textrm{rate}}{[\mathrm{NO}]^2[\mathrm{O_2}]}=\dfrac{15.9\times10^{-3}\textrm{ M/s}}{(0.0235\textrm{ M})^2(0.0250\textrm{ M})}=1.15\times10^3\;\mathrm{ M^{-2}\cdot s^{-1}} \nonumber \]
The difference is minor and associated with significant digits and likely experimental error in making the table.
The overall reaction order \((m + n) = 3\), so this is a third-order reaction whose rate is determined by three reactants. The units of the rate constant become more complex as the overall reaction order increases.
The peroxydisulfate ion (S2O82−) is a potent oxidizing agent that reacts rapidly with iodide ion in water:
\[S_2O^{2−}_{8(aq)} + 3I^−_{(aq)} \rightarrow 2SO^{2−}_{4(aq)} + I^−_{3(aq)} \nonumber \]
The following table lists kinetics data for this reaction at 25°C. Determine the rate law and calculate the rate constant.
| Experiment | [S2O82−]0 (M) | [I−]0 (M) | Initial Rate (M/s) |
|---|---|---|---|
| 1 | 0.27 | 0.38 | 2.05 |
| 2 | 0.40 | 0.38 | 3.06 |
| 3 | 0.40 | 0.22 | 1.76 |
- Answer:
- rate = k[S2O82−][I−]; k = 20 M−1·s−1
A Video Discussing Initial Rates and Rate Law Expressions. Video Link: Initial Rates and Rate Law Expressions(opens in new window) [youtu.be]
Summary
The rate law for a reaction is a mathematical relationship between the reaction rate and the concentrations of species in solution. Rate laws can be expressed either as a differential rate law, describing the change in reactant or product concentrations as a function of time, or as an integrated rate law, describing the actual concentrations of reactants or products as a function of time. The rate constant (k) of a rate law is a constant of proportionality between the reaction rate and the reactant concentration. The exponent to which a concentration is raised in a rate law indicates the reaction order, the degree to which the reaction rate depends on the concentration of a particular reactant.

