9.6: Problems
- Last updated
- Save as PDF
- Page ID
- 401396
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Some of the problems that follow require one or more equilibrium constants or standard state potentials. For your convenience, here are hyperlinks to the appendices containing these constants:
Appendix 10: Solubility Products
Appendix 11: Acid Dissociation Constants
1. Calculate or sketch titration curves for the following acid–base titrations.
(a) 25.0 mL of 0.100 M NaOH with 0.0500 M HCl
(b) 50.0 mL of 0.0500 M HCOOH with 0.100 M NaOH
(c) 50.0 mL of 0.100 M NH3 with 0.100 M HCl
(d) 50.0 mL of 0.0500 M ethylenediamine with 0.100 M HCl
(e) 50.0 mL of 0.0400 M citric acid with 0.120 M NaOH
(f) 50.0 mL of 0.0400 M H3PO4 with 0.120 M NaOH
2. Locate the equivalence point(s) for each titration curve in problem 1 and, where feasible, calculate the pH at the equivalence point. What is the stoichiometric relationship between the moles of acid and the moles of base for each of these equivalence points?
3. Suggest an appropriate visual indicator for each of the titrations in problem 1.
4. To sketch the titration curve for a weak acid we approximate the pH at 10% of the equivalence point volume as pKa – 1, and the pH at 90% of the equivalence point volume as pKa + 1. Show that these assumptions are reasonable.
5. Tartaric acid, H2C4H4O6, is a diprotic weak acid with a pKa1 of 3.0 and a pKa2 of 4.4. Suppose you have a sample of impure tartaric acid (purity > 80%), and that you plan to determine its purity by titrating with a solution of 0.1 M NaOH using an indicator to signal the end point. Describe how you will carry out the analysis, paying particular attention to how much sample to use, the desired pH range for the indicator, and how you will calculate the %w/w tartaric acid. Assume your buret has a maximum capacity of 50 mL.
6. The following data for the titration of a monoprotic weak acid with a strong base were collected using an automatic titrator. Prepare normal, first derivative, second derivative, and Gran plot titration curves for this data, and locate the equivalence point for each.
| volume of NaOH (mL) | pH | volume of NaOH (mL) | pH |
|---|---|---|---|
|
0.25 |
3.0 | 49.95 | 7.8 |
|
0.86 |
3.2 | 49.97 | 8.0 |
|
1.63 |
3.4 | 49.98 | 8.2 |
|
2.72 |
3.6 | 49.99 | 8.4 |
|
4.29 |
3.8 | 50.00 | 8.7 |
|
6.54 |
4.0 | 50.01 | 9.1 |
|
9.67 |
4.2 | 50.02 | 9.4 |
| 13.79 | 4.4 | 50.04 | 9.6 |
| 18.83 | 4.6 | 50.06 | 9.8 |
| 24.47 | 4.8 | 50.10 | 10.0 |
| 30.15 | 5.0 | 50.16 | 10.2 |
| 35.33 | 5.2 | 50.25 | 10.4 |
| 39.62 | 5.4 | 50.40 | 10.6 |
| 42.91 | 5.6 | 50.63 | 10.8 |
| 45.28 | 5.8 | 51.01 | 11.0 |
| 46.91 | 6.0 | 51.61 | 11.2 |
| 48.01 | 6.2 | 52.58 | 11.4 |
| 48.72 | 6.4 | 54.15 | 11.6 |
| 49.19 | 6.6 | 56.73 | 11.8 |
| 49.48 | 6.8 | 61.11 | 12.0 |
| 49.67 | 7.0 | 68.83 | 12.2 |
| 49.79 | 7.2 | 83.54 | 12.4 |
| 49.87 | 7.4 | 116.14 | 12.6 |
| 49.92 | 7.6 |
7. Schwartz published the following simulated data for the titration of a \(1.02 \times 10^{-4}\) M solution of a monoprotic weak acid (pKa = 8.16) with \(1.004 \times 10^{-3}\) M NaOH [Schwartz, L. M. J. Chem. Educ. 1992, 69, 879–883]. The simulation assumes that a 50-mL pipet is used to transfer a portion of the weak acid solution to the titration vessel. A calibration of the pipet shows that it delivers a volume of only 49.94 mL. Prepare normal, first derivative, second derivative, and Gran plot titration curves for this data, and determine the equivalence point for each. How do these equivalence points compare to the expected equivalence point? Comment on the utility of each titration curve for the analysis of very dilute solutions of very weak acids.
| mL of NaOH | pH | mL of NaOH | pH |
|---|---|---|---|
|
0.03 |
6.212 |
4.79 |
8.858 |
|
0.09 |
6.504 | 4.99 | 8.926 |
|
0.29 |
6.936 | 5.21 |
8.994 |
|
0.72 |
7.367 | 5.41 | 9.056 |
| 1.06 | 7.567 | 5.61 | 9.118 |
| 1.32 | 7.685 | 5.85 | 9.180 |
| 1.53 | 7.776 | 6.05 | 9.231 |
| 1.76 | 7.863 | 6.28 | 9.283 |
| 1.97 | 7.938 | 6.47 | 9.327 |
| 2.18 | 8.009 | 6.71 | 9.374 |
| 2.38 | 8.077 | 6.92 | 9.414 |
| 2.60 | 8.146 | 7.15 | 9.451 |
| 2.79 | 8.208 | 7.36 | 9.484 |
| 3.01 | 8.273 | 7.56 | 9.514 |
| 3.19 | 8.332 | 7.79 | 9.545 |
| 3.41 | 8.398 | 7.99 | 9.572 |
| 3.60 | 8.458 | 8.21 | 9.599 |
| 3.80 | 8.521 | 8.44 | 9.624 |
| 3.99 | 8.584 | 8.64 | 9.645 |
| 4.18 | 8.650 | 8.84 | 9.666 |
| 4.40 | 8.720 | 9.07 | 9.688 |
| 4.57 | 8.784 | 9.27 | 9.706 |
8. Calculate or sketch the titration curve for a 50.0 mL solution of a 0.100 M monoprotic weak acid (pKa = 8.0) with 0.1 M strong base in a nonaqueous solvent with Ks = \(10^{-20}\). You may assume that the change in solvent does not affect the weak acid’s pKa. Compare your titration curve to the titration curve when water is the solvent.
9. The titration of a mixture of p-nitrophenol (pKa = 7.0) and m-nitrophenol (pKa = 8.3) is followed spectrophotometrically. Neither acid absorbs at a wavelength of 545 nm, but their respective conjugate bases do absorb at this wavelength. The m-nitrophenolate ion has a greater absorbance than an equimolar solution of the p-nitrophenolate ion. Sketch the spectrophotometric titration curve for a 50.00-mL mixture consisting of 0.0500 M p-nitrophenol and 0.0500 M m-nitrophenol with 0.100 M NaOH. Compare your result to the expected potentiometric titration curves.
10. A quantitative analysis for aniline (C6H5NH2, Kb = \(3.94 \times 10^{-10}\)) is carried out by an acid–base titration using glacial acetic acid as the solvent and HClO4 as the titrant. A known volume of sample that contains 3–4 mmol of aniline is transferred to a 250-mL Erlenmeyer flask and diluted to approximately 75 mL with glacial acetic acid. Two drops of a methyl violet indicator are added, and the solution is titrated with previously standardized 0.1000 M HClO4 (prepared in glacial acetic acid using anhydrous HClO4) until the end point is reached. Results are reported as parts per million aniline.
(a) Explain why this titration is conducted using glacial acetic acid as the solvent instead of using water.
(b) One problem with using glacial acetic acid as solvent is its relatively high coefficient of thermal expansion of 0.11%/oC. For example, 100.00 mL of glacial acetic acid at 25oC occupies 100.22 mL at 27oC. What is the effect on the reported concentration of aniline if the standardization of HClO4 is conducted at a temperature that is lower than that for the analysis of the unknown?
(c) The procedure calls for a sample that contains 3–4 mmoles of aniline. Why is this requirement necessary?
Some of the problems that follow require one or more equilibrium constants or standard state potentials. For your convenience, here are hyperlinks to the appendices containing these constants:
Appendix 10: Solubility Products
Appendix 11: Acid Dissociation Constants
11. Using a ladder diagram, explain why the presence of dissolved CO2 leads to a determinate error for the standardization of NaOH if the end point’s pH is between 6–10, but no determinate error if the end point’s pH is less than 6.
12. A water sample’s acidity is determined by titrating to fixed end point pHs of 3.7 and 8.3, with the former providing a measure of the concentration of strong acid and the later a measure of the combined concentrations of strong acid and weak acid. Sketch a titration curve for a mixture of 0.10 M HCl and 0.10 M H2CO3 with 0.20 M strong base, and use it to justify the choice of these end points.
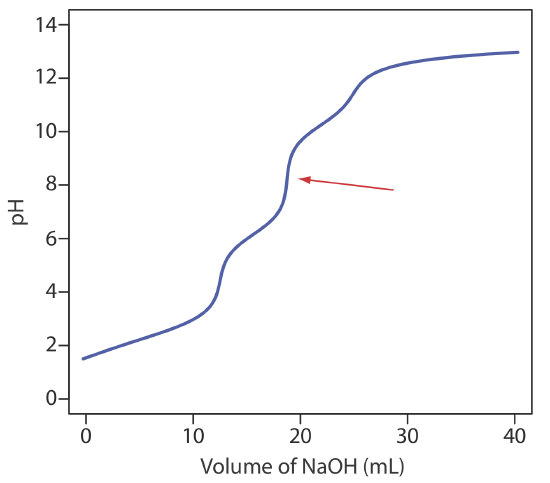
13. Ethylenediaminetetraacetic acid, H4Y, is a weak acid with successive acid dissociation constants of 0.010, \(2.19 \times 10^{-3}\), \(6.92 \times 10^{-7}\), and \(5.75 \times 10^{-11}\). The figure below shows a titration curve for H4Y with NaOH. What is the stoichiometric relationship between H4Y and NaOH at the equivalence point marked with the red arrow?
14. A Gran plot method has been described for the quantitative analysis of a mixture that consists of a strong acid and a monoprotic weak acid [(a) Boiani, J. A. J. Chem. Educ. 1986, 63, 724–726; (b) Castillo, C. A.; Jaramillo, A. J. Chem. Educ. 1989, 66, 341]. A 50.00-mL mixture of HCl and CH3COOH is transferred to an Erlenmeyer flask and titrated by using a digital pipet to add successive 1.00-mL aliquots of 0.09186 M NaOH. The progress of the titration is monitored by recording the pH after each addition of titrant. Using the two papers listed above as a reference, prepare a Gran plot for the following data and determine the concentrations of HCl and CH3COOH.
| mL of NaOH | pH | mL of NaOH | pH | mL of NaOH | pH |
|---|---|---|---|---|---|
|
1.00 |
1.83 |
24.00 |
4.45 |
47.00 |
12.14 |
|
2.00 |
1.86 |
25.00 |
4.53 |
48.00 |
12.17 |
|
3.00 |
1.89 |
26.00 |
4.61 |
49.00 |
12.20 |
|
4.00 |
1.92 |
27.00 |
4.69 |
50.00 |
12.23 |
|
5.00 |
1.95 |
28.00 |
4.76 |
51.00 |
12.26 |
|
6.00 |
1.99 |
29.00 |
4.84 |
52.00 |
12.28 |
|
7.00 |
2.03 |
30.00 |
4.93 |
53.00 |
12.30 |
|
8.00 |
2.10 |
31.00 |
5.02 |
54.00 |
12.32 |
|
9.00 |
2.18 |
32.00 |
5.13 |
55.00 |
12.34 |
|
10.00 |
2.31 | 33.00 |
5.23 |
56.00 |
12.36 |
| 11.00 | 2.51 | 34.00 |
5.37 |
57.00 |
12.38 |
| 12.00 | 2.81 | 35.00 |
5.52 |
58.00 |
12.39 |
| 13.00 | 3.16 | 36.00 |
5.75 |
59.00 |
12.40 |
| 14.00 | 3.36 | 37.00 |
6.14 |
60.00 |
12.42 |
| 15.00 | 3.54 | 38.00 |
10.30 |
61.00 | 12.43 |
| 16.00 | 3.69 | 39.00 | 11.31 | 62.00 | 12.44 |
| 17.00 | 3.81 | 40.00 | 11.58 | 63.00 | 12.45 |
| 18.00 | 3.93 | 41.00 | 11.74 | 64.00 | 12.47 |
| 19.00 | 4.02 | 42.00 | 11.85 | 65.00 | 12.48 |
| 20.00 | 4.14 | 43.00 | 11.93 | 66.00 | 12.49 |
| 21.00 | 4.22 | 44.00 | 12.00 | 67.00 | 12.50 |
| 22.00 | 4.30 | 45.00 | 12.05 | 68.00 | 12.51 |
| 23.00 | 4.38 | 46.00 | 12.10 | 69.00 | 12.52 |
15. Explain why it is not possible for a sample of water to simultaneously have OH– and \(\text{HCO}_3^-\) as sources of alkalinity.
16. For each of the samples a–e, determine the sources of alkalinity (OH–, \(\text{HCO}_3^-\), \(\text{CO}_3^{2-}\)) and their respective concentrations in parts per million In each case a 25.00-mL sample is titrated with 0.1198 M HCl to the bromocresol green and the phenolphthalein end points.
| sample | volume of HCl (mL) to phenolphthalein end point | volume of HCl (mL) to the bromocresol green end point |
|---|---|---|
| a | 21.36 | 21.38 |
| b | 5.67 | 21.13 |
| c | 0.00 | 14.28 |
| d | 17.12 | 34.26 |
| e | 21.36 | 25.69 |
17. A sample may contain any of the following: HCl, NaOH, H3PO4, \(\text{H}_2\text{PO}_4^-\), \(\text{HPO}_4^{2-}\), or \(\text{PO}_4^{3-}\). The composition of a sample is determined by titrating a 25.00-mL portion with 0.1198 M HCl or 0.1198 M NaOH to the phenolphthalein and to the methyl orange end points. For each of the following samples, determine which species are present and their respective molar concentrations.
| sample | titrant | volume (mL) to phenophthalein end point | volume (mL) to methyl orange end point |
|---|---|---|---|
| a | HCl | 11.54 | 35.29 |
| b | NaOH | 19.79 | 9.89 |
| c | HCl | 22.76 | 22.78 |
| d | NaOH | 39.42 | 17.48 |
18. The protein in a 1.2846-g sample of an oat cereal is determined by a Kjeldahl analysis. The sample is digested with H2SO4, the resulting solution made basic with NaOH, and the NH3 distilled into 50.00 mL of 0.09552 M HCl. The excess HCl is back titrated using 37.84 mL of 0.05992 M NaOH. Given that the proteins in grains average 17.54% w/w N, report the %w/w protein in the sample.
19. The concentration of SO2 in air is determined by bubbling a sample of air through a trap that contains H2O2. Oxidation of SO2 by H2O2 results in the formation of H2SO4, which is then determined by titrat-ing with NaOH. In a typical analysis, a sample of air is passed through the peroxide trap at a rate of 12.5 L/min for 60 min and required 10.08 mL of 0.0244 M NaOH to reach the phenolphthalein end point. Calculate the μL/L SO2 in the sample of air. The density of SO2 at the temperature of the air sample is 2.86 mg/mL.
20. The concentration of CO2 in air is determined by an indirect acid–base titration. A sample of air is bubbled through a solution that contains an excess of Ba(OH)2, precipitating BaCO3. The excess Ba(OH)2 is back titrated with HCl. In a typical analysis a 3.5-L sample of air is bubbled through 50.00 mL of 0.0200 M Ba(OH)2. Back titrating with 0.0316 M HCl requires 38.58 mL to reach the end point. Determine the ppm CO2 in the sample of air given that the density of CO2 at the temperature of the sample is 1.98 g/L.
Some of the problems that follow require one or more equilibrium constants or standard state potentials. For your convenience, here are hyperlinks to the appendices containing these constants:
Appendix 10: Solubility Products
Appendix 11: Acid Dissociation Constants
21. The purity of a synthetic preparation of methylethyl ketone, C4H8O, is determined by reacting it with hydroxylamine hydrochloride, liberating HCl (see reaction in Table 9.2.7). In a typical analysis a 3.00-mL sample is diluted to 50.00 mL and treated with an excess of hydroxylamine hydrochloride. The liberated HCl is titrated with 0.9989 M NaOH, requiring 32.68 mL to reach the end point. Report the percent purity of the sample given that the density of methylethyl ketone is 0.805 g/mL.
22. Animal fats and vegetable oils are triesters formed from the reaction between glycerol (1,2,3-propanetriol) and three long-chain fatty acids. One of the methods used to characterize a fat or an oil is a determination of its saponification number. When treated with boiling aqueous KOH, an ester saponifies into the parent alcohol and fatty acids (as carboxylate ions). The saponification number is the number of milligrams of KOH required to saponify 1.000 gram of the fat or the oil. In a typical analysis a 2.085-g sample of butter is added to 25.00 mL of 0.5131 M KOH. After saponification is complete the excess KOH is back titrated with 10.26 mL of 0.5000 M HCl. What is the saponification number for this sample of butter?
23. A 250.0-mg sample of an organic weak acid is dissolved in an appropriate solvent and titrated with 0.0556 M NaOH, requiring 32.58 mL to reach the end point. Determine the compound’s equivalent weight.
24. The figure below shows a potentiometric titration curve for a 0.4300-g sample of a purified amino acid that was dissolved in 50.00 mL of water and titrated with 0.1036 M NaOH. Identify the amino acid from the possibilities listed in the table.

| amino acid | formula weight (g/mol) | Ka |
|---|---|---|
| alanine | 89.1 | \(1.35 \times 10^{-10}\) |
| glycine | 75.1 | \(1.67 \times 10^{-10}\) |
| methionine | 149.2 | \(8.9 \times 10^{-10}\) |
| taurine | 125.2 | \(1.8 \times 10^{-9}\) |
| asparagine | 150 | \(1.9 \times 10^{-9}\) |
| leucine | 131.2 | \(1.79 \times 10^{-10}\) |
| phenylalanine | 166.2 | \(4.9 \times 10^{-10}\) |
| valine | 117.2 | \(1.91 \times 10^{-10}\) |
25. Using its titration curve, determine the acid dissociation constant for the weak acid in problem 9.6.
26. Where in the scale of operations do the microtitration techniques discussed in Chapter 9.7 belong?
27. An acid–base titration can be used to determine an analyte’s equivalent weight, but it can not be used to determine its formula weight. Explain why.
28. Commercial washing soda is approximately 30–40% w/w Na2CO3. One procedure for the quantitative analysis of washing soda contains the following instructions:
Transfer an approximately 4-g sample of the washing soda to a 250-mL volumetric flask. Dissolve the sample in about 100 mL of H2O and then dilute to the mark. Using a pipet, transfer a 25-mL aliquot of this solution to a 125-mL Erlenmeyer flask and add 25-mL of H2O and 2 drops of bromocresol green indicator. Titrate the sample with 0.1 M HCl to the indicator’s end point.
What modifications, if any, are necessary if you want to adapt this procedure to evaluate the purity of commercial Na2CO3 that is >98% pure?
29. A variety of systematic and random errors are possible when standardizing a solution of NaOH against the primary weak acid standard potassium hydrogen phthalate (KHP). Identify, with justification, whether the following are sources of systematic error or random error, or if they have no affect on the error. If the error is systematic, then indicate whether the experimentally determined molarity for NaOH is too high or too low. The standardization reaction is
\[\text{C}_8\text{H}_5\text{O}_4^-(aq) + \text{OH}^-(aq) \rightarrow \text{C}_8\text{H}_4\text{O}_4^-(aq) + \text{H}_2\text{O}(l) \nonumber\]
(a) The balance used to weigh KHP is not properly calibrated and always reads 0.15 g too low.
(b) The indicator for the titration changes color between a pH of 3–4.
(c) An air bubble, which is lodged in the buret’s tip at the beginning of the analysis, dislodges during the titration.
(d) Samples of KHP are weighed into separate Erlenmeyer flasks, but the balance is tarred only for the first flask.
(e) The KHP is not dried before it is used.
(f) The NaOH is not dried before it is used.
(g) The procedure states that the sample of KHP should be dissolved in 25 mL of water, but it is accidentally dissolved in 35 mL of water.
30. The concentration of o-phthalic acid in an organic solvent, such as n-butanol, is determined by an acid–base titration using aqueous NaOH as the titrant. As the titrant is added, the o-phthalic acid extracts into the aqueous solution where it reacts with the titrant. The titrant is added slowly to allow sufficient time for the extraction to take place.
(a) What type of error do you expect if the titration is carried out too quickly?
(b) Propose an alternative acid–base titrimetric method that allows for a more rapid determination of the concentration of o-phthalic acid in n-butanol.
Some of the problems that follow require one or more equilibrium constants or standard state potentials. For your convenience, here are hyperlinks to the appendices containing these constants:
Appendix 10: Solubility Products
Appendix 11: Acid Dissociation Constants
31. Calculate or sketch titration curves for 50.0 mL of 0.100 Mg2+ with 0.100 M EDTA at a pH of 7 and 10. Locate the equivalence point for each titration curve.
32. Calculate or sketch titration curves for 25.0 mL of 0.0500 M Cu2+ with 0.025 M EDTA at a pH of 10 and in the presence of 10–3 M and 10–1 M NH3. Locate the equivalence point for each titration curve.
33. Sketch the spectrophotometric titration curve for the titration of a mixture of \(5.00 \times 10^{-3}\) M Bi3+ and \(5.00 \times 10^{-3}\) M Cu2+ with 0.0100 M EDTA. Assume that only the Cu2+–EDTA complex absorbs at the selected wavelength.
34. The EDTA titration of mixtures of Ca2+ and Mg2+ can be followed thermometrically because the formation of the Ca2+–EDTA complex is exothermic and the formation of the Mg2+–EDTA complex is endothermic. Sketch the thermometric titration curve for a mixture of \(5.00 \times 10^{-3}\) M Ca2+ and \(5.00 \times 10^{-3}\) M Mg2+ using 0.0100 M EDTA as the titrant. The heats of formation for CaY2– and MgY2– are, respectively, –23.9 kJ/mole and 23.0 kJ/mole.
35. EDTA is one member of a class of aminocarboxylate ligands that form very stable 1:1 complexes with metal ions. The following table provides logKf values for the complexes of six such ligands with Ca2+ and Mg2+. Which ligand is the best choice for a direct titration of Ca2+ in the presence of Mg2+?
| ligand | Mg2+ | Ca2+ |
|---|---|---|
| EDTA: ethylenediaminetetraacetica acid | 8.7 | 10.7 |
| HEDTA: N-hydroxyethylenediametriacetic acid | 7.0 | 8.0 |
| EEDTA: ethyletherdiaminetetraacetic acid | 8.3 | 10.0 |
| EGTA: ethyleneglycol-bis(\(\beta\)-aminoethylether)-N,N'-tetraacetic acid | 5.4 | 10.9 |
| DTPA: diethylenetriaminpentaacetic acid | 9.0 | 107 |
| CyDTA: cycloheanediaminetetraacetic acid | 10.3 | 12.3 |
36. The amount of calcium in physiological fluids is determined by a complexometric titration with EDTA. In one such analysis a 0.100-mL sample of a blood serum is made basic by adding 2 drops of NaOH and titrated with 0.00119 M EDTA, requiring 0.268 mL to reach the end point. Report the concentration of calcium in the sample as milligrams Ca per 100 mL.
37. After removing the membranes from an eggshell, the shell is dried and its mass recorded as 5.613 g. The eggshell is transferred to a 250-mL beaker and dissolved in 25 mL of 6 M HCl. After filtering, the solution that contains the dissolved eggshell is diluted to 250 mL in a volumetric flask. A 10.00-mL aliquot is placed in a 125-mL Erlenmeyer flask and buffered to a pH of 10. Titrating with 0.04988 M EDTA requires 44.11 mL to reach the end point. Determine the amount of calcium in the eggshell as %w/w CaCO3.
38. The concentration of cyanide, CN–, in a copper electroplating bath is determined by a complexometric titration using Ag+ as the titrant, forming the soluble \(\text{Ag(CN)}_2^-\) complex. In a typical analysis a 5.00-mL sample from an electroplating bath is transferred to a 250-mL Erlenmeyer flask, and treated with 100 mL of H2O, 5 mL of 20% w/v NaOH and 5 mL of 10% w/v KI. The sample is titrated with 0.1012 M AgNO3, requiring 27.36 mL to reach the end point as signaled by the formation of a yellow precipitate of AgI. Report the concentration of cyanide as parts per million of NaCN.
39. Before the introduction of EDTA most complexation titrations used Ag+ or CN– as the titrant. The analysis for Cd2+, for example, was accomplished indirectly by adding an excess of KCN to form \(\text{Cd(CN)}_4^{2-}\), and back-titrating the excess CN– with Ag+, forming \(\text{Ag(CN)}_2^-\). In one such analysis a 0.3000-g sample of an ore is dissolved and treated with 20.00 mL of 0.5000 M KCN. The excess CN– requires 13.98 mL of 0.1518 M AgNO3 to reach the end point. Determine the %w/w Cd in the ore.
40. Solutions that contain both Fe3+ and Al3+ are selectively analyzed for Fe3+ by buffering to a pH of 2 and titrating with EDTA. The pH of the solution is then raised to 5 and an excess of EDTA added, resulting in the formation of the Al3+–EDTA complex. The excess EDTA is back-titrated using a standard solution of Fe3+, providing an indirect analysis for Al3+.
(a) At a pH of 2, verify that the formation of the Fe3+–EDTA complex is favorable, and that the formation of the Al3+–EDTA complex is not favorable.
(b) A 50.00-mL aliquot of a sample that contains Fe3+ and Al3+ is transferred to a 250-mL Erlenmeyer flask and buffered to a pH of 2. A small amount of salicylic acid is added, forming the soluble red-colored Fe3+–salicylic acid complex. The solution is titrated with 0.05002 M EDTA, requiring 24.82 mL to reach the end point as signaled by the disappearance of the Fe3+–salicylic acid complex’s red color. The solution is buffered to a pH of 5 and 50.00 mL of 0.05002 M EDTA is added. After ensuring that the formation of the Al3+–EDTA complex is complete, the excess EDTA is back titrated with 0.04109 M Fe3+, requiring 17.84 mL to reach the end point as signaled by the reappearance of the red-colored Fe3+–salicylic acid complex. Report the molar concentrations of Fe3+ and Al3+ in the sample.
Some of the problems that follow require one or more equilibrium constants or standard state potentials. For your convenience, here are hyperlinks to the appendices containing these constants:
Appendix 10: Solubility Products
Appendix 11: Acid Dissociation Constants
41. Prada and colleagues described an indirect method for determining sulfate in natural samples, such as seawater and industrial effluents [Prada, S.; Guekezian, M.; Suarez-Iha, M. E. V. Anal. Chim. Acta 1996, 329, 197–202]. The method consists of three steps: precipitating the sulfate as PbSO4; dissolving the PbSO4 in an ammonical solution of excess EDTA to form the soluble PbY2– complex; and titrating the excess EDTA with a standard solution of Mg2+. The following reactions and equilibrium constants are known
\[\text{PbSO}_4(s) \rightleftharpoons \text{Pb}^{2+}(aq) + \text{SO}_4^{2-}(aq) \quad K_\text{sp} = 1.6 \times 10^{-8} \nonumber\]
\[\text{Pb}^{2+}(aq) + \text{Y}^{4-}(aq) \rightleftharpoons \text{PbY}^{2-}(aq) \quad K_\text{f} = 1.1 \times 10^{18} \nonumber\]
\[\text{Mg}^{2+}(aq) + \text{Y}^{4-}(aq) \rightleftharpoons \text{MgY}^{2-}(aq) \quad K_\text{f} = 4.9 \times 10^{8} \nonumber\]
\[\text{Zn}^{2+}(aq) + \text{Y}^{4-}(aq) \rightleftharpoons \text{ZnY}^{2-}(aq) \quad K_\text{f} = 3.2 \times 10^{16} \nonumber\]
(a) Verify that a precipitate of PbSO4 will dissolve in a solution of Y4–.
(b) Sporek proposed a similar method using Zn2+ as a titrant and found that the accuracy frequently was poor [Sporek, K. F. Anal. Chem. 1958, 30, 1030–1032]. One explanation is that Zn2+ might react with the PbY2– complex, forming ZnY2–. Show that this might be a problem when using Zn2+ as a titrant, but that it is not a problem when using Mg2+ as a titrant. Would such a displacement of Pb2+ by Zn2+ lead to the reporting of too much or too little sulfate?
(c) In a typical analysis, a 25.00-mL sample of an industrial effluent is carried through the procedure using 50.00 mL of 0.05000 M EDTA. Titrating the excess EDTA requires 12.42 mL of 0.1000 M Mg2+. Report the molar concentration of \(\text{SO}_4^{2-}\) in the sample of effluent.
42. Table 9.3.1 provides values for the fraction of EDTA present as Y4–, \(\alpha_{\text{Y}^{4-}}\). Values of \(\alpha_{\text{Y}^{4-}}\) are calculated using the equation
\[\alpha_{\text{Y}^{4-}} = \frac{[\text{Y}^{4-}]}{C_\text{EDTA}} \nonumber\]
where [Y4-] is the concentration of the fully deprotonated EDTA and CEDTA is the total concentration of EDTA in all of its forms
\[C_\text{EDTA} = [\text{H}_6\text{Y}^{2+}]+[\text{H}_5\text{Y}^{+}]+[\text{H}_4\text{Y}]+ [\text{H}_3\text{Y}^{-}] + [\text{H}_2\text{Y}^{2-}] + [\text{H}_\text{Y}^{3-}] + [\text{Y}^{4-}] \nonumber\]
\[\text{H}_6\text{Y}^{2+} (aq) + \text{H}_2\text{O}(l) \rightleftharpoons \text{H}_3\text{O}^+(aq) + \text{H}_5\text{Y}^{+}(aq) \quad K_\text{a1} \nonumber\]
\[\text{H}_5\text{Y}^{+} (aq) + \text{H}_2\text{O}(l) \rightleftharpoons \text{H}_3\text{O}^+(aq) + \text{H}_4\text{Y}(aq) \quad K_\text{a2} \nonumber\]
\[\text{H}_4\text{Y} (aq) + \text{H}_2\text{O}(l) \rightleftharpoons \text{H}_3\text{O}^+(aq) + \text{H}_3\text{Y}^{-}(aq) \quad K_\text{a3} \nonumber\]
\[\text{H}_3\text{Y}^{-} (aq) + \text{H}_2\text{O}(l) \rightleftharpoons \text{H}_3\text{O}^+(aq) + \text{H}_2\text{Y}^{2-}(aq) \quad K_\text{a4} \nonumber\]
\[\text{H}_2\text{Y}^{2-} (aq) + \text{H}_2\text{O}(l) \rightleftharpoons \text{H}_3\text{O}^+(aq) + \text{H}\text{Y}^{3-}(aq) \quad K_\text{a5} \nonumber\]
\[\text{H}\text{Y}^{2-} (aq) + \text{H}_2\text{O}(l) \rightleftharpoons \text{H}_3\text{O}^+(aq) + \text{Y}^{4-}(aq) \quad K_\text{a6} \nonumber\]
to show that
\[\alpha_{\text{Y}^{4-}} = \frac{K_\text{a1}K_\text{a2}K_\text{a3}K_\text{a4}K_\text{a5}K_\text{a6}}{d} \nonumber\]
where
\[d = [\text{H}_3\text{O}^+]^6 + [\text{H}_3\text{O}^+]^5K_\text{a1} + [\text{H}_3\text{O}^+]^4K_\text{a1}K_\text{a2} + [\text{H}_3\text{O}^+]^3K_\text{a1}K_\text{a2}K_\text{a3} + [\text{H}_3\text{O}^+]^2K_\text{a1}K_\text{a2}K_\text{a3}K_\text{a4} + [\text{H}_3\text{O}^+]K_\text{a1}K_\text{a2}K_\text{a3}K_\text{a4}K_\text{a5} + K_\text{a1}K_\text{a2}K_\text{a3}K_\text{a4}K_\text{a5}K_\text{a6} \nonumber\]
43. Calculate or sketch titration curves for the following redox titration reactions at 25oC. Assume the analyte initially is present at a concentration of 0.0100 M and that a 25.0-mL sample is taken for analysis. The titrant, which is the bold species in each reaction, has a concentration of 0.0100 M.
(a) V2+(aq) + Ce4+(aq) \(\rightarrow\) V3+(aq) + Ce3+(aq)
(b) Sn2+(aq) + 2Ce4+(aq) \(\rightarrow\) Sn4+(aq) +2Ce3+(aq)
(c) 5Fe2+(aq) + \(\mathbf{MnO}_\mathbf{4}^\mathbf{-}\)(aq) + 8H+(aq) \(\rightarrow\) 5Fe3+(aq) + Mn2+(aq) +4H2O(l) at a pH of 1
44. What is the equivalence point for each titration in problem 43?
45. Suggest an appropriate indicator for each titration in problem 43.
46. The iron content of an ore is determined by a redox titration that uses K2Cr2O7 as the titrant. A sample of the ore is dissolved in concentrated HCl using Sn2+ to speed its dissolution by reducing Fe3+ to Fe2+. After the sample is dissolved, Fe2+ and any excess Sn2+ are oxidized to Fe3+ and Sn4+ using \(\text{MnO}_4^-\). The iron is then carefully reduced to Fe2+ by adding a 2–3 drop excess of Sn2+. A solution of HgCl2 is added and, if a white precipitate of Hg2Cl2 forms, the analysis is continued by titrating with K2Cr2O7. The sample is discarded without completing the analysis if a precipitate of Hg2Cl2 does not form or if a gray precipitate (due to Hg) forms.
(a) Explain why the sample is discarded if a white precipitate of Hg2Cl2 does not form or if a gray precipitate forms.
(b) Is a determinate error introduced if the analyst forgets to add Sn2+ in the step where the iron ore is dissolved?
(c) Is a determinate error introduced if the iron is not quantitatively oxidized back to Fe3+ by the \(\text{MnO}_4^-\)?
47. The amount of Cr3+ in an inorganic salt is determined by a redox titration. A portion of sample that contains approximately 0.25 g of Cr3+ is accurately weighed and dissolved in 50 mL of H2O. The Cr3+ is oxidized to \(\text{Cr}_2\text{O}_7^{2-}\) by adding 20 mL of 0.1 M AgNO3, which serves as a catalyst, and 50 mL of 10%w/v (NH4)2S2O8, which serves as the oxidizing agent. After the reaction is complete, the resulting solution is boiled for 20 minutes to destroy the excess \(\text{S}_2\text{O}_8^{2-}\), cooled to room temperature, and diluted to 250 mL in a volumetric flask. A 50-mL portion of the resulting solution is transferred to an Erlenmeyer flask, treated with 50 mL of a standard solution of Fe2+, and acidified with 200 mL of 1 M H2SO4, reducing the \(\text{Cr}_2\text{O}_7^{2-}\) to Cr3+. The excess Fe2+ is then determined by a back titration with a standard solution of K2Cr2O7 using an appropriate indicator. The results are reported as %w/w Cr3+.
(a) There are several places in the procedure where a reagent’s volume is specified (see italicized text). Which of these measurements must be made using a volumetric pipet.
(b) Excess peroxydisulfate, \(\text{S}_2\text{O}_8^{2-}\) is destroyed by boiling the solution. What is the effect on the reported %w/w Cr3+ if some of the \(\text{S}_2\text{O}_8^{2-}\) is not destroyed during this step?
(c) Solutions of Fe2+ undergo slow air oxidation to Fe3+. What is the effect on the reported %w/w Cr3+ if the standard solution of Fe2+ is inadvertently allowed to be partially oxidized?
48. The exact concentration of H2O2 in a solution that is nominally 6% w/v H2O2 is determined by a redox titration using \(\text{MnO}_4^-\) as the titrant. A 25-mL aliquot of the sample is transferred to a 250-mL volumetric flask and diluted to volume with distilled water. A 25-mL aliquot of the diluted sample is added to an Erlenmeyer flask, diluted with 200 mL of distilled water, and acidified with 20 mL of 25% v/v H2SO4. The resulting solution is titrated with a standard solution of KMnO4 until a faint pink color persists for 30 s. The results are reported as %w/v H2O2.
(a) Many commercially available solutions of H2O2 contain an inorganic or an organic stabilizer to prevent the autodecomposition of the peroxide to H2O and O2. What effect does the presence of this stabilizer have on the reported %w/v H2O2 if it also reacts with \(\text{MnO}_4^-\)?
(b) Laboratory distilled water often contains traces of dissolved organic material that may react with \(\text{MnO}_4^-\). Describe a simple method to correct for this potential interference.
(c) What modifications to the procedure, if any, are needed if the sample has a nominal concentration of 30% w/v H2O2.
49. The amount of iron in a meteorite is determined by a redox titration using KMnO4 as the titrant. A 0.4185-g sample is dissolved in acid and the liberated Fe3+ quantitatively reduced to Fe2+ using a Walden reductor. Titrating with 0.02500 M KMnO4 requires 41.27 mL to reach the end point. Determine the %w/w Fe2O3 in the sample of meteorite.
50. Under basic conditions, \(\text{MnO}_4^-\) is used as a titrant for the analysis of Mn2+, with both the analyte and the titrant forming MnO2. In the analysis of a mineral sample for manganese, a 0.5165-g sample is dissolved and the manganese reduced to Mn2+. The solution is made basic and titrated with 0.03358 M KMnO4, requiring 34.88 mL to reach the end point. Calculate the %w/w Mn in the mineral sample.
Some of the problems that follow require one or more equilibrium constants or standard state potentials. For your convenience, here are hyperlinks to the appendices containing these constants:
Appendix 10: Solubility Products
Appendix 11: Acid Dissociation Constants
51. The amount of uranium in an ore is determined by an indirect redox titration. The analysis is accomplished by dissolving the ore in sulfuric acid and reducing \(\text{UO}_2^+\) to U4+ with a Walden reductor. The solution is treated with an excess of Fe3+, forming Fe2+ and U6+. The Fe2+ is titrated with a standard solution of K2Cr2O7. In a typical analysis a 0.315-g sample of ore is passed through the Walden reductor and treated with 50.00 mL of 0.0125 M Fe3+. Back titrating with 0.00987 M K2Cr2O7 requires 10.52 mL. What is the %w/w U in the sample?
52. The thickness of the chromium plate on an auto fender is determined by dissolving a 30.0-cm2 section in acid and oxidizing Cr3+ to \(\text{Cr}_2\text{O}_7^{2-}\) with peroxydisulfate. After removing excess peroxydisulfate by boiling, 500.0 mg of Fe(NH4)2(SO4)2•6H2O is added, reducing the \(\text{Cr}_2\text{O}_7^{2-}\) to Cr3+. The excess Fe2+ is back titrated, requiring 18.29 mL of 0.00389 M K2Cr2O7 to reach the end point. Determine the average thickness of the chromium plate given that the density of Cr is 7.20 g/cm3.
53. The concentration of CO in air is determined by passing a known volume of air through a tube that contains I2O5, forming CO2 and I2. The I2 is removed from the tube by distilling it into a solution that contains an excess of KI, producing \(\text{I}_3^-\). The \(\text{I}_3^-\) is titrated with a standard solution of Na2S2O3. In a typical analysis a 4.79-L sample of air is sampled as described here, requiring 7.17 mL of 0.00329 M Na2S2O3 to reach the end point. If the air has a density of \(1.23 \times 10^{-3}\) g/mL, determine the parts per million CO in the air.
54. The level of dissolved oxygen in a water sample is determined by the Winkler method. In a typical analysis a 100.0-mL sample is made basic and treated with a solution of MnSO4, resulting in the formation of MnO2. An excess of KI is added and the solution is acidified, resulting in the formation of Mn2+ and I2. The liberated I2 is titrated with a solution of 0.00870 M Na2S2O3, requiring 8.90 mL to reach the starch indicator end point. Calculate the concentration of dissolved oxygen as parts per million O2.
55. Calculate or sketch the titration curve for the titration of 50.0 mL of 0.0250 M KI with 0.0500 M AgNO3. Prepare separate titration curves using pAg and pI on the y-axis.
56. Calculate or sketch the titration curve for the titration of a 25.0 mL mixture of 0.0500 M KI and 0.0500 M KSCN using 0.0500 M AgNO3 as the titrant.
57. The analysis for Cl– using the Volhard method requires a back titration. A known amount of AgNO3 is added, precipitating AgCl. The unreacted Ag+ is determined by back titrating with KSCN. There is a complication, however, because AgCl is more soluble than AgSCN.
(a) Why do the relative solubilities of AgCl and AgSCN lead to a titration error?
(b) Is the resulting titration error a positive or a negative determinate error?
(c) How might you modify the procedure to eliminate this source of determinate error?
(d) Is this source of determinate error of concern when using the Volhard method to determine Br–?
58. Voncina and co-workers suggest that a precipitation titration can be monitored by measuring pH as a function of the volume of titrant if the titrant is a weak base [VonČina, D. B.; DobČnik, D.; GomiŠČek, S. Anal. Chim. Acta 1992, 263, 147–153]. For example, when titrating Pb2+ with K2CrO4 the solution that contains the analyte initially is acidified to a pH of 3.50 using HNO3. Before the equivalence point the concentration of \(\text{CrO}_4^{2-}\) is controlled by the solubility product of PbCrO4. After the equivalence point the concentration of \(\text{CrO}_4^{2-}\) is determined by the amount of excess titrant. Considering the reactions that control the concentration of \(\text{CrO}_4^{2-}\), sketch the expected titration curve of pH versus volume of titrant.
59. A 0.5131-g sample that contains KBr is dissolved in 50 mL of distilled water. Titrating with 0.04614 M AgNO3 requires 25.13 mL to reach the Mohr end point. A blank titration requires 0.65 mL to reach the same end point. Report the %w/w KBr in the sample.
60. A 0.1093-g sample of impure Na2CO3 is analyzed by the Volhard method. After adding 50.00 mL of 0.06911 M AgNO3, the sample is back titrated with 0.05781 M KSCN, requiring 27.36 mL to reach the end point. Report the purity of the Na2CO3 sample.
61. A 0.1036-g sample that contains only BaCl2 and NaCl is dissolved in 50 mL of distilled water. Titrating with 0.07916 M AgNO3 requires 19.46 mL to reach the Fajans end point. Report the %w/w BaCl2 in the sample.
Some of the problems that follow require one or more equilibrium constants or standard state potentials. For your convenience, here are hyperlinks to the appendices containing these constants:
Appendix 10: Solubility Products
Appendix 11: Acid Dissociation Constants


