11.1: Internal Energy
- Page ID
- 238253
The internal energy of a system is identified with the random, disordered motion of molecules; the total (internal) energy in a system includes potential and kinetic energy. This is contrast to external energy which is a function of the sample with respect to the outside environment (e.g. kinetic energy if the sample is moving or potential energy if the sample is at a height from the ground etc). The symbol for Internal Energy Change is \( ΔU\).
Energy on a smaller scale
- Internal energy includes energy on a microscopic scale
- It is the sum of all the microscopic energies such as:
- translational kinetic energy
- vibrational and rotational kinetic energy
- potential energy from intermolecular forces
| Example |
|---|
|
One gram of water at zero °Celsius compared with one gram of copper at zero °Celsius do NOT have the same internal energy because even though their kinetic energies are equal, water has a much higher potential energy causing its internal energy to be much greater than the copper's internal energy. |
Internal Energy Change Equations
The first law of thermodynamics states:
\[dU=dq+dw\]
where \(dq\) is heat and \(dw\) is work.
An isolated system cannot exchange heat or work with its surroundings making the change in internal energy equal to zero:
\[dU_{\text {isolated system}} = 0\]
Therefore, in an isolated system:
\[dq=-dw\]
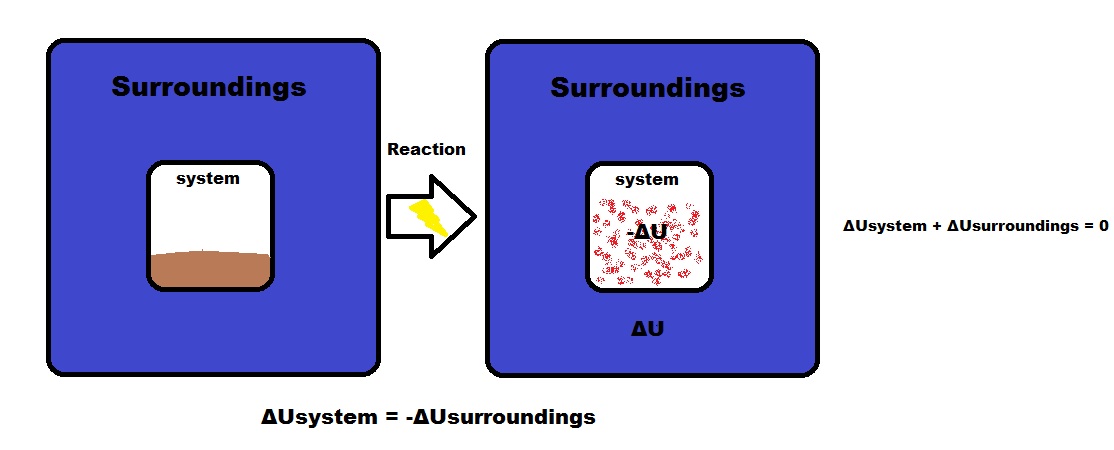
Energy is Conserved
\[dU_{\text {isolated system}} = dU_{\text {system}} + dU_{\text {surroundings}}\]
\[dU_{\text {system}}= -dU_{\text {surroundings}}\]
The signs of internal energy
- Energy entering the system is POSITIVE (+), meaning heat is absorbed, q>0. Work is thus done on the system, w>0
- Energy leaving the system is NEGATIVE (-), meaning heat is given off by the system, q<0 and work is done by the system, w<0
Quick Notes
- A system contains ONLY Internal Energy
- A system does NOT contain energy in the form of heat or work
- Heat and work only exist during a change in the system; they are path functions
- Internal energy is a state function
Outside Links
- Levine, Ira N. "Thermodynamic internal energy of an ideal gas of rigid rotors." J. Chem. Educ. 1985: 62, 53.
Contributors
- Lorraine Alborzfar (UCD)