Skip to main content
Chemistry LibreTexts

4.10: Mole Road Map

  1. Last updated
  2. Save as PDF
  • Page ID
    367775

    • Anonymous
    • LibreTexts
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    If you want to visit the town of Manteo, North Carolina, out on the coast, you need a map to get there. You may have a printed map or may download directions from the internet, but need something to steer you in the right direction. Chemistry road maps serve the same purpose. How do you handle a certain type of calculation? There is a process and a set of directions to help.

    Mole Road Map

    The mole concept is central to any chemistry calculation based on experimental results. The mole is how we relate the unbelievably small atoms and molecules that make something up to the measurable properties such as mass which we may observe in a laboratory setting. In this chapter, we have limited our discussion on the mole concept to the measurable property of masses of pure substances. However, this is not the only type of matter that exists. In later chapters, we will need to consider how to find the moles of a portion of matter which may not be a pure substance, or may be difficult to mass. Or we may need to find how the amount of substance changes as a result of a chemical change. Having a way to map conversion factors between moles and various properties becomes important as we introduce these other ways of measuring matter.

    The following diagram shows a mole map which includes one additional measurable property (the volume of the gas at STP). You do not need to understand the meaning of STP at the moment, and we will explore gas properties in more detail in a later chapter. However, you should be able to look at the diagram and see how the mole concept is central. As additional conversions between moles and measurable properties are introduced in later chapters, please take a moment to create your own mole map showing how those properties relate to the mole concept via a conversion factor.

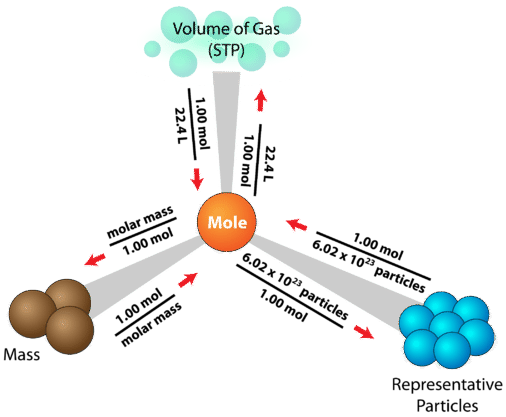
    CK12 Screenshot 10-9-1.png
    Figure \(\PageIndex{1}\): The mole road map shows the conversion factors needed to interconvert mass, number of particles, and volume of a gas.

    The mole is at the center of any calculation involving amount of a substance. The sample problem below is one of many different problems that can be solved using the mole road map.

    Example \(\PageIndex{1}\)

    What is the volume of \(79.3 \: \text{g}\) of neon gas at STP?

    Solution

    Step 1: List the known quantities and plan the problem.

    Known

    • \(\ce{Ne} = 20.18 \: \text{g/mol}\)
    • \(1 \: \text{mol} = 22.4 \: \text{L}\)

    Unknown

    The conversion factors will be grams \(\rightarrow\) moles \(\rightarrow\) gas volume.

    Step 2: Calculate.

    \[79.3 \: \text{g} \: \ce{Ne} \times \frac{1 \: \text{mol} \: \ce{Ne}}{20.18 \: \text{g} \: \ce{Ne}} \times \frac{22.4 \: \text{L} \: \ce{Ne}}{1 \: \text{mol} \: \ce{Ne}} = 88.0 \: \text{L} \: \ce{Ne}\]

    Step 3: Think about your result.

    The given mass of neon is equal to about 4 moles, resulting in a volume that is about 4 times larger than molar volume.

    Summary

    This page titled 4.10: Mole Road Map is shared under a mixed license and was authored, remixed, and/or curated by Anonymous via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.