14.5: Nuclear Equations

Learning Objectives

• Write and balance nuclear equations.

A balanced chemical reaction equation reflects the fact that during a chemical reaction, bonds break and form, and atoms are rearranged, but the total numbers of atoms of each element are conserved and do not change. A balanced nuclear reaction equation indicates that there is a rearrangement during a nuclear reaction, but of subatomic particles rather than atoms. Nuclear reactions also follow conservation laws, and they are balanced in two ways:

1. The sum of the mass numbers of the reactants equals the sum of the mass numbers of the products.
2. The sum of the charges of the reactants equals the sum of the charges of the products.

If the atomic number and the mass number of all but one of the particles in a nuclear reaction are known, we can identify the particle by balancing the reaction. For instance, we could determine that \(\ce{^{17}_8O}\) is a product of the nuclear reaction of \(\ce{^{14}_7N}\) and \(\ce{^4_2He}\) if we knew that a proton, \(\ce{^1_1H}\), was one of the two products. Example \(\PageIndex{1}\) shows how we can identify a nuclide by balancing the nuclear reaction.

Example \(\PageIndex{1}\): Balancing Equations for Nuclear Reactions

The reaction of an α particle with magnesium-25 \( (\ce{^{25}_{12}Mg})\) produces a proton and a nuclide of another element. Identify the new nuclide produced.

Solution

The nuclear reaction can be written as:

\[\ce{^{25}_{12}Mg + ^4_2He \rightarrow ^1_1H + ^{A}_{Z}X} \nonumber \]

where

• \(\ce A\) is the mass number and
• \(\ce Z\) is the atomic number of the new nuclide, \(\ce X\).

Because the sum of the mass numbers of the reactants must equal the sum of the mass numbers of the products:

\[\mathrm{25+4=A+1} \nonumber \]

so

\[ \mathrm{A=28} \nonumber \]

Similarly, the charges must balance, so:

\[\mathrm{12+2=Z+1} \nonumber \]

so

\[\mathrm{Z=13} \nonumber \]

Check the periodic table: The element with nuclear charge = +13 is aluminum. Thus, the product is \(\ce{^{28}_{13}Al}\).

Exercise \(\PageIndex{1}\)

The nuclide \(\ce{^{125}_{53}I}\) combines with an electron and produces a new nucleus and no other massive particles. What is the equation for this reaction?

Answer

\[\ce{^{125}_{53}I + ^0_{−1}e \rightarrow ^{125}_{52}Te} \nonumber \]

The two general kinds of nuclear reactions are nuclear decay reactions and nuclear transmutation reactions. In a nuclear decay reaction, also called radioactive decay, an unstable nucleus emits radiation and is transformed into the nucleus of one or more other elements. The resulting daughter nuclei have a lower mass and are lower in energy (more stable) than the parent nucleus that decayed. In contrast, in a nuclear transmutation reaction, a nucleus reacts with a subatomic particle or another nucleus to form a product nucleus that is more massive than the starting material. As we shall see, nuclear decay reactions occur spontaneously under all conditions, but nuclear transmutation reactions occur only under very special conditions, such as the collision of a beam of highly energetic particles with a target nucleus or in the interior of stars. We begin this section by considering the different classes of radioactive nuclei, along with their characteristic nuclear decay reactions and the radiation they emit.

Nuclear decay reactions occur spontaneously under all conditions, whereas nuclear transmutation reactions are induced.

Nuclear Decay Reactions

Just as we use the number and type of atoms present to balance a chemical equation, we can use the number and type of nucleons present to write a balanced nuclear equation for a nuclear decay reaction. This procedure also allows us to predict the identity of either the parent or the daughter nucleus if the identity of only one is known. Regardless of the mode of decay, the total number of nucleons is conserved in all nuclear reactions.

To describe nuclear decay reactions, chemists have extended the \(^A _Z \textrm{X}\) notation for nuclides to include radioactive emissions. Table \(\PageIndex{1}\) lists the name and symbol for each type of emitted radiation. The most notable addition is the positron, a particle that has the same mass as an electron but a positive charge rather than a negative charge.

Table \(\PageIndex{1}\): Nuclear Decay Emissions and Their Symbols

Identity	Symbol	Charge	Mass (amu)
helium nucleus	\(^4_2\alpha\)	+2	4.001506
electron	\(^0_{-1}\beta\) or \(\beta ^-\)	−1	0.000549
photon	\(_0^0\gamma\)	—	—
neutron	\(^1_0\textrm n\)	0	1.008665
proton	\(^1_1\textrm p \)	+1	1.007276
positron	\(^0_{+1}\beta\) or \(\beta ^+\)	+1	0.000549

Like the notation used to indicate isotopes, the upper left superscript in the symbol for a particle gives the mass number, which is the total number of protons and neutrons. For a proton or a neutron, A = 1. Because neither an electron nor a positron contains protons or neutrons, its mass number is 0. The numbers should not be taken literally, however, as meaning that these particles have zero mass; ejection of a beta particle (an electron) simply has a negligible effect on the mass of a nucleus.

Similarly, the lower left subscript gives the charge of the particle. Because protons carry a positive charge, Z = +1 for a proton. In contrast, a neutron contains no protons and is electrically neutral, so Z = 0. In the case of an electron, Z = −1, and for a positron, Z = +1. Because γ rays are high-energy photons, both A and Z are 0. In some cases, two different symbols are used for particles that are identical but produced in different ways. For example, the symbol \(^0_{-1}\textrm e\), which is usually simplified to e⁻, represents a free electron or an electron associated with an atom, whereas the symbol \(^0_{-1}\beta\), which is often simplified to β⁻, denotes an electron that originates from within the nucleus, which is a β particle. Similarly, \(^4_{2}\textrm{He}^{2+}\) refers to the nucleus of a helium atom, and \(^4_{2}\alpha\) denotes an identical particle that has been ejected from a heavier nucleus.

There are six fundamentally different kinds of nuclear decay reactions, and each releases a different kind of particle or energy. The essential features of each reaction are shown in Figure \(\PageIndex{1}\). The most common are alpha and beta decay and gamma emission, but the others are essential to an understanding of nuclear decay reactions.

Figure \(\PageIndex{1}\): Common Modes of Nuclear Decay

The different types of decay are alpha, beta, positron emission, electron capture, gamma emission, and spontaneous fission.

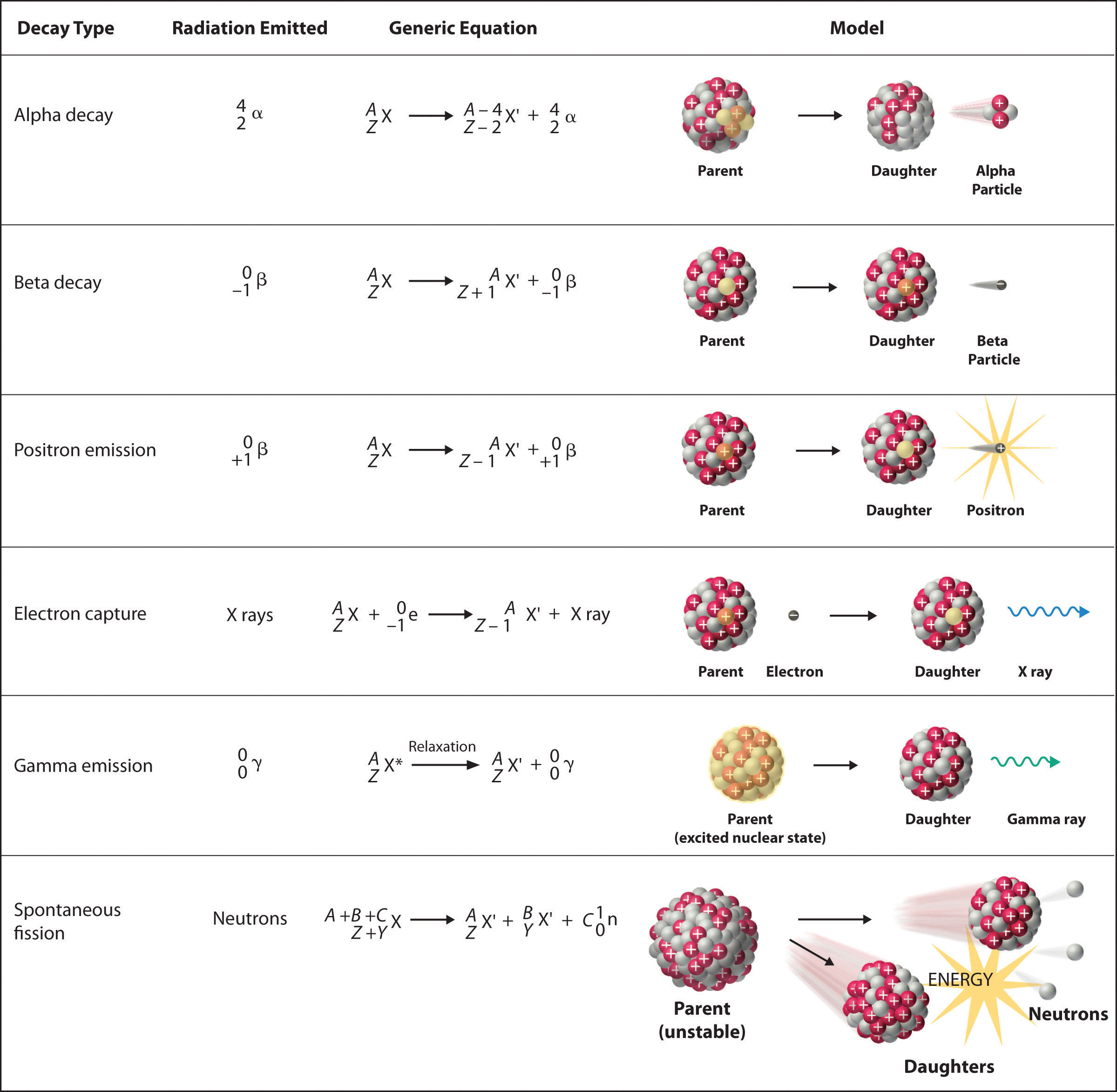
Alpha \(\alpha\) Decay

Many nuclei with mass numbers greater than 200 undergo alpha (α) decay, which results in the emission of a helium-4 nucleus as an alpha (α) particle, \(^4_{2}\alpha\). The general reaction is as follows:

\[\underset{\textrm{parent}}{^A_Z \textrm X}\rightarrow \underset{\textrm{daughter}}{^{A-4}_{Z-2} \textrm X'}+\underset{\textrm{alpha}\\ \textrm{particle}}{^4_2 \alpha}\label{Eq1} \]

The daughter nuclide contains two fewer protons and two fewer neutrons than the parent. Thus, α-particle emission produces a daughter nucleus with a mass number A − 4 and a nuclear charge Z − 2 compared to the parent nucleus. Radium-226, for example, undergoes alpha decay to form radon-222:

\[^{226}_{88}\textrm{Ra}\rightarrow ^{222}_{86}\textrm{Rn}+^{4}_{2}\alpha\label{Eq2} \]

Because nucleons are conserved in this and all other nuclear reactions, the sum of the mass numbers of the products, 222 + 4 = 226, equals the mass number of the parent. Similarly, the sum of the atomic numbers of the products, 86 + 2 = 88, equals the atomic number of the parent. Thus, the nuclear equation is balanced.

Just as the total number of atoms is conserved in a chemical reaction, the total number of nucleons is conserved in a nuclear reaction.

Beta \(\beta^-\) Decay

Nuclei that contain too many neutrons often undergo beta (β) decay, in which a neutron is converted to a proton and a high-energy electron that is ejected from the nucleus as a β particle:

\[\underset{\textrm{unstable} \\ \textrm{neutron in} \\ \textrm{nucleus}}{^1_0 \textrm n}\rightarrow \underset{\textrm{proton} \\ \textrm{retained} \\ \textrm{by nucleus}}{^{1}_{1} \textrm p}+\underset{\textrm{beta particle} \\ \textrm{emitted by} \\ \textrm{nucleus}}{^0_{-1} \beta}\label{Eq3} \]

The general reaction for beta decay is therefore

\[\underset{\textrm{parent}}{^A_Z \textrm X}\rightarrow \underset{\textrm{daughter}}{^{A}_{Z+1} \textrm X'}+\underset{\textrm{beta particle}}{^0_{-1} \beta}\label{Eq4} \]

Although beta decay does not change the mass number of the nucleus, it does result in an increase of +1 in the atomic number because of the addition of a proton in the daughter nucleus. Thus, beta decay decreases the neutron-to-proton ratio, moving the nucleus toward the band of stable nuclei. For example, carbon-14 undergoes beta decay to form nitrogen-14:

\[^{14}_{6}\textrm{C}\rightarrow ^{14}_{7}\textrm{N}+\,^{0}_{-1}\beta \nonumber \]

Once again, the number of nucleons is conserved, and the charges are balanced. The parent and the daughter nuclei have the same mass number, 14, and the sum of the atomic numbers of the products is 6, which is the same as the atomic number of the carbon-14 parent.

Positron \(\beta^+\) Emission

Because a positron has the same mass as an electron but opposite charge, positron emission is the opposite of beta decay. Thus positron emission is characteristic of neutron-poor nuclei, which decay by transforming a proton to a neutron and emitting a high-energy positron:

\[^{1}_{1}\textrm{p}^+\rightarrow ^{1}_{0}\textrm{n}+\,^{0}_{+1}\beta^+\label{Eq6} \]

The general reaction for positron emission is therefore

\[\underset{\textrm{parent}}{^A_Z \textrm X}\rightarrow \underset{\textrm{daughter}}{^{A}_{Z-1} \textrm X'}+\underset{\textrm{positron}}{^0_{+1} \beta^+} \nonumber \]

Like beta decay, positron emission does not change the mass number of the nucleus. In this case, however, the atomic number of the daughter nucleus is lower by 1 than that of the parent. Thus, the neutron-to-proton ratio has increased, again moving the nucleus closer to the band of stable nuclei. For example, carbon-11 undergoes positron emission to form boron-11:

\[^{11}_{6}\textrm{C}\rightarrow ^{11}_{5}\textrm{B}+\,^{0}_{+1}\beta^+ \nonumber \]

Nucleons are conserved, and the charges balance. The mass number, 11, does not change, and the sum of the atomic numbers of the products is 6, the same as the atomic number of the parent carbon-11 nuclide.

Electron Capture

A neutron-poor nucleus can decay by either positron emission or electron capture (EC), in which an electron in an inner shell reacts with a proton to produce a neutron:

\[^{1}_{1}\textrm{p} +\; ^{0}_{-1}\textrm{e}\rightarrow \, ^{1}_{0}\textrm n\label{Eq9} \]

When a second electron moves from an outer shell to take the place of the lower-energy electron that was absorbed by the nucleus, an x-ray is emitted. The overall reaction for electron capture is thus

\[\underset{\textrm{parent}}{^A_Z \textrm X}+\underset{\textrm{electron}}{^0_{-1} \textrm e}\rightarrow \underset{\textrm{daughter}}{^{A}_{Z-1} \textrm X'}+\textrm{x-ray} \nonumber \]

Electron capture does not change the mass number of the nucleus because both the proton that is lost and the neutron that is formed have a mass number of 1. As with positron emission, however, the atomic number of the daughter nucleus is lower by 1 than that of the parent. Once again, the neutron-to-proton ratio has increased, moving the nucleus toward the band of stable nuclei. For example, iron-55 decays by electron capture to form manganese-55, which is often written as follows:

\[^{55}_{26}\textrm{Fe}\overset{\textrm{EC}}{\rightarrow}\, ^{55}_{25}\textrm{Mn}+\textrm{x-ray} \nonumber \]

The atomic numbers of the parent and daughter nuclides differ in Equation 20.2.11, although the mass numbers are the same. To write a balanced nuclear equation for this reaction, we must explicitly include the captured electron in the equation:

\[^{55}_{26}\textrm{Fe}+\,^{0}_{-1}\textrm{e}\rightarrow \, ^{55}_{25}\textrm{Mn}+\textrm{x-ray} \nonumber \]

Both positron emission and electron capture are usually observed for nuclides with low neutron-to-proton ratios, but the decay rates for the two processes can be very different.

Gamma \(\gamma\) Emission

Many nuclear decay reactions produce daughter nuclei that are in a nuclear excited state, which is similar to an atom in which an electron has been excited to a higher-energy orbital to give an electronic excited state. Just as an electron in an electronic excited state emits energy in the form of a photon when it returns to the ground state, a nucleus in an excited state releases energy in the form of a photon when it returns to the ground state. These high-energy photons are γ rays. Gamma (\(\gamma\)) emission can occur virtually instantaneously, as it does in the alpha decay of uranium-238 to thorium-234, where the asterisk denotes an excited state:

\[^{238}_{92}\textrm{U}\rightarrow \, \underset{\textrm{excited} \\ \textrm{nuclear} \\ \textrm{state}}{^{234}_{90}\textrm{Th*}} + ^{4}_{2}\alpha\xrightarrow {\textrm{relaxation}\,}\,^{234}_{90}\textrm{Th} + \ce{^0_0\gamma} \nonumber \]

If we disregard the decay event that created the excited nucleus, then

\[^{234}_{88}\textrm{Th*} \rightarrow\, ^{234}_{88}\textrm{Th} + ^{0}_{0}\gamma \nonumber \]

or more generally,

\[^{A}_{Z}\textrm{X*} \rightarrow\, ^{A}_{Z}\textrm{X} + ^{0}_{0}\gamma \nonumber \]

Gamma emission can also occur after a significant delay. For example, technetium-99m has a half-life of about 6 hours before emitting a \(γ\) ray to form technetium-99 (the m is for metastable). Because γ rays are energy, their emission does not affect either the mass number or the atomic number of the daughter nuclide. Gamma-ray emission is therefore the only kind of radiation that does not necessarily involve the conversion of one element to another, although it is almost always observed in conjunction with some other nuclear decay reaction.

Example \(\PageIndex{2}\)

Write a balanced nuclear equation to describe each reaction.

1. the beta decay of \(^{35}_{16}\textrm{S}\)
2. the decay of \(^{201}_{80}\textrm{Hg}\) by electron capture
3. the decay of \(^{30}_{15}\textrm{P}\) by positron emission

Given: radioactive nuclide and mode of decay

Asked for: balanced nuclear equation

Strategy:

A Identify the reactants and the products from the information given.

B Use the values of A and Z to identify any missing components needed to balance the equation.

Solution

a.

A We know the identities of the reactant and one of the products (a β particle). We can therefore begin by writing an equation that shows the reactant and one of the products and indicates the unknown product as \(^{A}_{Z}\textrm{X}\): \[^{35}_{16}\textrm{S}\rightarrow\,^{A}_{Z}\textrm{X}+\,^{0}_{-1}\beta \nonumber \]

B Because both protons and neutrons must be conserved in a nuclear reaction, the unknown product must have a mass number of A = 35 − 0 = 35 and an atomic number of Z = 16 − (−1) = 17. The element with Z = 17 is chlorine, so the balanced nuclear equation is as follows: \[^{35}_{16}\textrm{S}\rightarrow\,^{35}_{17}\textrm{Cl}+\,^{0}_{-1}\beta \nonumber \]

b.

A We know the identities of both reactants: \(^{201}_{80}\textrm{Hg}\) and an inner electron, \(^{0}_{-1}\textrm{e}\). The reaction is as follows: \[^{201}_{80}\textrm{Hg}+\,^{0}_{-1}\textrm e\rightarrow\,^{A}_{Z}\textrm{X} \nonumber \]

B Both protons and neutrons are conserved, so the mass number of the product must be A = 201 + 0 = 201, and the atomic number of the product must be Z = 80 + (−1) = 79, which corresponds to the element gold. The balanced nuclear equation is thus \[^{201}_{80}\textrm{Hg}+\,^{0}_{-1}\textrm e\rightarrow\,^{201}_{79}\textrm{Au} \nonumber \]

c.

A As in part (a), we are given the identities of the reactant and one of the products—in this case, a positron. The unbalanced nuclear equation is therefore \[^{30}_{15}\textrm{P}\rightarrow\,^{A}_{Z}\textrm{X}+\,^{0}_{+1}\beta \nonumber \]

B The mass number of the second product is A = 30 − 0 = 30, and its atomic number is Z = 15 − 1 = 14, which corresponds to silicon. The balanced nuclear equation for the reaction is as follows: \[^{30}_{15}\textrm{P}\rightarrow\,^{30}_{14}\textrm{Si}+\,^{0}_{+1}\beta \nonumber \]

Exercise \(\PageIndex{2}\)

Write a balanced nuclear equation to describe each reaction.

1. \(^{11}_{6}\textrm{C}\) by positron emission
2. the beta decay of molybdenum-99
3. the emission of an α particle followed by gamma emission from \(^{185}_{74}\textrm{W}\)

Answer a

\(^{11}_{6}\textrm{C}\rightarrow\,^{11}_{5}\textrm{B}+\,^{0}_{+1}\beta\)

Answer d

\(^{99}_{42}\textrm{Mo}\rightarrow\,^{99m}_{43}\textrm{Tc}+\,^{0}_{-1}\beta\)

Answer c

\(^{185}_{74}\textrm{W}\rightarrow\,^{181}_{72}\textrm{Hf}+\,^{4}_{2}\alpha +\,^{0}_{0}\gamma\)

Radioactive Decay Series

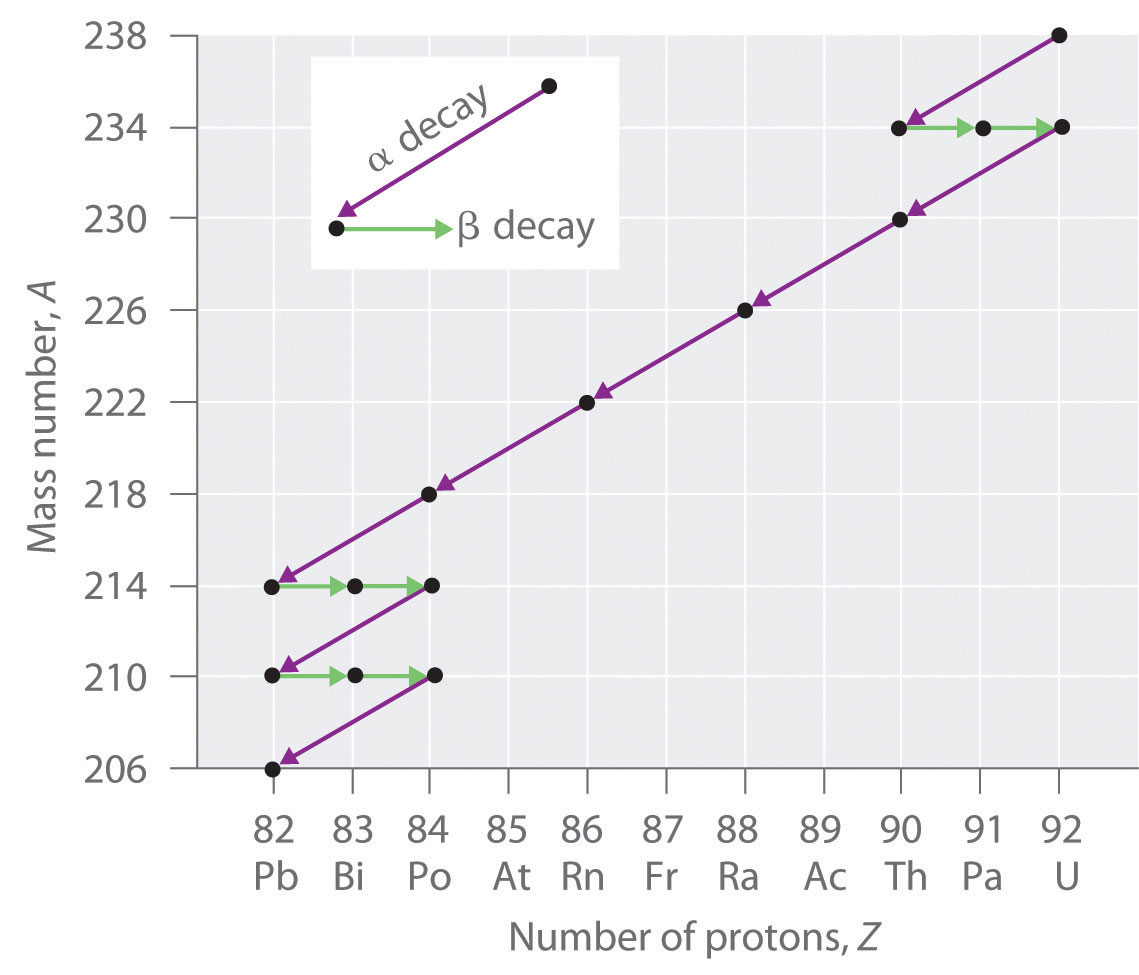
The nuclei of all elements with atomic numbers greater than 83 are unstable. Thus, all isotopes of all elements beyond bismuth in the periodic table are radioactive. Because alpha decay decreases Z by only 2, and positron emission or electron capture decreases Z by only 1, it is impossible for any nuclide with Z > 85 to decay to a stable daughter nuclide in a single step, except via nuclear fission. Consequently, radioactive isotopes with Z > 85 usually decay to a daughter nucleus that is radiaoctive, which in turn decays to a second radioactive daughter nucleus, and so forth, until a stable nucleus finally results. This series of sequential alpha- and beta-decay reactions is called a radioactive decay series. We will discuss some of the implications of the naturally occuring decay series later in this chapter as we address half-life.

Figure \(\PageIndex{2}\) A Radioactive Decay Series. Three naturally occurring radioactive decay series are known to occur currently: the uranium-238 decay series, the decay of uranium-235 to lead-207, and the decay of thorium-232 to lead-208.

Graph of mass number against number of protons. The purple lines are alpha decay which are linear while the green lines are beta decay and are horizontal and parallel to the x axis.

Nuclear Transmutation Reactions

The same process of balancing the masses in nuclear decay reactions can also be effective in balancing more complicated nuclear reactions. These include induced nuclear transmutations as well as some naturally occurring processes. Induced nuclear transmutations are necessary for the synthesis of elements with more protons than uranium (92), and are referred to as transuranium elements. We will explore two additional types of nuclear transmutation later in this chapter: fission, and fusion. Both of these can be either induced or naturally occurring.

Section Summary

• Nuclear equations are balanced by making sure the number of protons and neutrons remain the same on both sides of the reaction.
• Nuclear reactions might be either naturally occurring or induced.

Glossary

nuclear decay reaction (radioactive decay)

An unstable nucleus spontaneously emits radiation and is transformed into the nucleus of one or more other elements.

nuclear transmutation reaction

a nucleus reacts with a subatomic particle or another nucleus to form a product nucleus that is more massive than the starting material.

radioactive decay series

series of sequential alpha- and beta-decay reactions that eventually results in a non-radioactive element.