12.9: Concentrations of Solutions
- Page ID
- 476622
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Calculate the concentration of a solution in either percent concentration or molarity.
Mixtures, including solutions, have variable compositions from one sample to another. Because of this variability, it becomes important in some cases to specify the amount of each substance present in a particular sample of a solution. We will explore some methods of keeping track of the amount of a substance present in a solution in this section.
Saturated and Unsaturated Solutions
Table salt \(\left( \ce{NaCl} \right)\) readily dissolves in water. Suppose that you have a beaker of water to which you add some salt, stirring until it dissolves. You add more and that dissolves. You keep adding more and more salt, eventually reaching a point at which no more of the salt will dissolve—no matter how long or how vigorously you stir it. Why? On the molecular level, we know that action of the water causes the individual ions to break apart from the salt crystal and enter the solution, where they remain hydrated by water molecules. What also happens is that some of the dissolved ions collide back again with the crystal and remain there. Recrystallization is the process of dissolved solute returning to the solid state. At some point, the rate at which the solid salt is dissolving becomes equal to the rate at which the dissolved solute is recrystallizing. When that point is reached, the total amount of dissolved salt remains unchanged. Solution equilibrium is the physical state described by the opposing processes of dissolution and recrystallization occurring at the same rate. The solution equilibrium for the dissolution of sodium chloride can be represented by one of two equations:
\[\ce{NaCl} \left( s \right) \rightleftharpoons \ce{NaCl} \left( aq \right)\nonumber \]
While the above equation shows the change of state back and forth between solid and aqueous solution, the preferred equation also shows the dissociation that occurs as an ionic solid dissolves:
\[\ce{NaCl} \left( s \right) \rightleftharpoons \ce{Na^+} \left( aq \right) + \ce{Cl^-} \left( aq \right)\nonumber \]
When the solution equilibrium point is reached and no more solute will dissolve, the solution is said to be saturated. A saturated solution is a solution that contains the maximum amount of solute that is capable of dissolving. At \(20^\text{o} \text{C}\), the maximum amount of \(\ce{NaCl}\) that will dissolve in \(100. \: \text{g}\) of water is \(36.0 \: \text{g}\). If any more \(\ce{NaCl}\) is added past this point, it will not dissolve, because the solution is saturated. What if more water is added to the solution instead? In that case, more \(\ce{NaCl}\) would be capable of dissolving in the additional solvent. An unsaturated solution is a solution that contains less than the maximum amount of solute that is capable of being dissolved. The figure below illustrates the above process and shows the distinction between unsaturated and saturated.
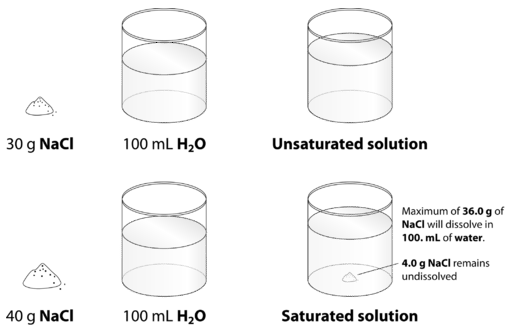
How can you tell if a solution is saturated or unsaturated? If more solute is added and it does not dissolve, then the original solution was saturated. If the added solute dissolves, then the original solution was unsaturated. A solution that has been allowed to reach equilibrium, but which has extra undissolved solute at the bottom of the container, must be saturated.
For solutions that are saturated, the amount of a substance present in it can be obtained from tabulated data for that substance at the given pressure and temperature. But most of the time we are not dealing with a saturated solution, so we want to be able to express this more generally.
Percent Solutions
One way to describe the concentration of a solution is by the percent of a solute in the solvent. The percent can further be determined in one of two ways: (1) the ratio of the mass of the solute divided by the mass of the solution or (2) the ratio of the volume of the solute divided by the volume of the solution.
Mass Percent
When the solute in a solution is a solid, a convenient way to express the concentration is by mass percent \(\left( \frac{\text{mass}}{\text{mass}} \right)\), which is the grams of solute per \(100 \: \text{g}\) of solution.
\[\text{Percent by mass} = \frac{\text{mass of solute}}{\text{mass of solution}} \times 100\%\nonumber \]
Suppose that a solution was prepared by dissolving \(25.0 \: \text{g}\) of sugar into \(100 \: \text{g}\) of water. The percent by mass would be calculated by:
\[\text{Percent by mass} = \frac{25 \: \text{g sugar}}{125 \: \text{g solution}} \times 100\% = 20\% \: \text{sugar}\nonumber \]
Sometimes you may want to make up a particular mass of solution of a given percent by mass, and need to calculate what mass of the solvent to use. For example, you need to make \(3000 \: \text{g}\) of a \(5\%\) solution of sodium chloride. You can rearrange and solve for the mass of solute:
\[\text{mass of solute} = \frac{\text{percent by mass}}{100\%} \times \text{mass of solution} = \frac{5\%}{100\%} \times 3000 \: \text{g} = 150 \: \text{g} \: \ce{NaCl}\nonumber \]
You would need to weigh out \(150 \: \text{g}\) of \(\ce{NaCl}\) and add it to \(2850 \: \text{g}\) of water. Notice that it was necessary to subtract the mass of the \(\ce{NaCl}\) \(\left( 150 \: \text{g} \right)\) from the mass of solution \(\left( 3000 \: \text{g} \right)\) to calculate the mass of the water that would need to be added.
Volume Percent
The percentage of solute in a solution can more easily be determined by volume when the solute and solvent are both liquids. The volume of the solute divided by the volume of the solution, expressed as a percent, yields the percent by volume \(\left( \frac{\text{volume}}{\text{volume}} \right)\) of the solution. If a solution is made by adding \(40 \: \text{mL}\) of ethanol to \(200 \: \text{mL}\) of water, the percent by volume is:
\[\begin{align*} \text{Percent by volume} &= \frac{\text{volume of solute}}{\text{volume of solution}} \times 100\% \\[8px] &= \frac{40 \: \text{mL ethanol}}{240 \: \text{mL solution}} \times 100\% \\[8px] &= 16.7\% \: \text{ethanol} \end{align*}\nonumber \]
Frequently, ingredient labels on food products and medicines have amounts listed as percentages (see figure below).

Molarity
Chemists primarily need the concentration of solutions to be expressed in a way that accounts for the number of particles that react according to a particular chemical equation. Since percentage measurements are based on either mass or volume, they are generally not useful for chemical reactions. A concentration unit based on moles is preferable. The molarity \(\left( \text{M} \right)\) of a solution is the number of moles of solute dissolved in one liter of solution. To calculate the molarity of a solution, divide the moles of solute by the volume of the solution expressed in liters:
\[\text{Molarity} \left( \text{M} \right) = \frac{\text{moles of solute}}{\text{liters of solution}} = \frac{\text{mol}}{\text{L}}\nonumber \]
Note that the volume is in liters of solution and not liters of solvent. When a molarity is reported, the unit is the symbol \(\text{M}\) and is read as "molar". For example a solution labeled as \(1.5 \: \text{M} \: \ce{NH_3}\) is read as "1.5 molar ammonia solution".
Example \(\PageIndex{1}\)
A solution is prepared by dissolving \(42.23 \: \text{g}\) of \(\ce{NH_4Cl}\) into enough water to make \(500.0 \: \text{mL}\) of solution. Calculate its molarity.
Solution
Step 1: List the known quantities and plan the problem.
Known
- Mass \(= 42.23 \: \text{g} \: \ce{NH_4Cl}\)
- Molar mass \(\ce{NH_4Cl} = 53.50 \: \text{g/mol}\)
- Volume solution \(= 500.0 \: \text{mL} = 0.5000 \: \text{L}\)
Unknown
The mass of the ammonium chloride is first converted to moles. Then the molarity is calculated by dividing by liters. Note that the given volume has been converted to liters.
Step 2: Solve.
\[\begin{align*} 42.23 \ \text{g} \: \ce{NH_4Cl} \times \frac{1 \: \text{mol} \: \ce{NH_4Cl}}{53.50 \: \text{g} \: \ce{NH_4Cl}} &= 0.7893 \: \text{mol} \: \ce{NH_4Cl} \\ \frac{0.7893 \: \text{mol} \: \ce{NH_4Cl}}{0.5000 \: \text{L}} &= 1.579 \: \text{M} \end{align*}\nonumber \]
Step 3: Think about your result.
The molarity is \(1.579 \: \text{M}\), meaning that a liter of the solution would contain \(1.579 \: \text{mol} \: \ce{NH_4Cl}\).
In a laboratory situation, a chemist must frequently prepare a given volume of solutions of a known molarity. The task is to calculate the mass of the solute that is necessary. The molarity equation can be rearranged to solve for moles, which can then be converted to grams.
Example \(\PageIndex{2}\)
A chemist needs to prepare \(3.00 \: \text{L}\) of a \(0.250 \: \text{M}\) solution of potassium permanganate \(\left( \ce{KMnO_4} \right)\). What mass of \(\ce{KMnO_4}\) does she need to make the solution?
Solution
Step 1: List the known quantities and plan the problem.
Known
- Molarity \(= 0.250 \: \text{M}\)
- Volume \(= 3.00 \: \text{L}\)
- Molar mass \(\ce{KMnO_4} = 158.04 \: \text{g/mol}\)
Unknown
Moles of solute is calculated by multiplying molarity by liters. Then, moles is converted to grams.
Step 2: Solve.
\[\begin{align*} \text{mol} \: \ce{KMnO_4} = 0.250 \: \text{M} \: \ce{KMnO_4} \times 3.00 \: \text{L} &= 0.750 \: \text{mol} \: \ce{KMnO_4} \\ 0.750 \: \text{mol} \: \ce{KMnO_4} \times \frac{158.04 \: \text{g} \: \ce{KMnO_4}}{1 \: \text{mol} \: \ce{KMnO_4}} &= 119 \: \text{g} \: \ce{KMnO_4} \end{align*}\nonumber \]
Step 3: Think about your result.
When \(119 \: \text{g}\) of potassium permanganate is dissolved into water to make \(3.00 \: \text{L}\) of solution, the molarity is \(0.250 \: \text{M}\).
Section Summary
- Techniques for calculation of percent mass and percent volume solution concentrations are described.
- The molarity \(\left( \text{M} \right)\) of a solution is the number of moles of solute dissolved in one liter of solution.
- Calculations using the concept of molarity are described.
Glossary
- recrystallization
- The process of dissolved solute returning to the solid state.
- solution equilibrium
- The physical state described by the opposing processes of dissolution and recrystallization occurring at the same rate.
- saturated solution
- A solution that contains the maximum amount of solute that is capable of dissolving.
- unsaturated solution
- A solution that contains less than the maximum amount of solute that is capable of being dissolved.
- concentration
- Measure of the amount of solute that has been dissolved in a given amount of solvent or solution.


