1.3: Molecular Orbitals and Covalent Bonds
- Page ID
- 58727
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To use molecular orbital theory to predict bond order
None of the approaches we have described so far can adequately explain why some compounds are colored and others are not, why some substances with unpaired electrons are stable, and why others are effective semiconductors. These approaches also cannot describe the nature of resonance. Such limitations led to the development of a new approach to bonding in which electrons are not viewed as being localized between the nuclei of bonded atoms but are instead delocalized throughout the entire molecule. Just as with the valence bond theory, the approach we are about to discuss is based on a quantum mechanical model.
Previously, we described the electrons in isolated atoms as having certain spatial distributions, called orbitals, each with a particular orbital energy. Just as the positions and energies of electrons in atoms can be described in terms of atomic orbitals (AOs), the positions and energies of electrons in molecules can be described in terms of molecular orbitals (MOs) A particular spatial distribution of electrons in a molecule that is associated with a particular orbital energy.—a spatial distribution of electrons in a molecule that is associated with a particular orbital energy. As the name suggests, molecular orbitals are not localized on a single atom but extend over the entire molecule. Consequently, the molecular orbital approach, called molecular orbital theory is a delocalized approach to bonding.
Molecular Orbital Theory: A Delocalized Bonding Approach
Although the molecular orbital theory is computationally demanding, the principles on which it is based are similar to those we used to determine electron configurations for atoms. The key difference is that in molecular orbitals, the electrons are allowed to interact with more than one atomic nucleus at a time. Just as with atomic orbitals, we create an energy-level diagram by listing the molecular orbitals in order of increasing energy. We then fill the orbitals with the required number of valence electrons according to the Pauli principle. This means that each molecular orbital can accommodate a maximum of two electrons with opposite spins.
Molecular Orbitals Involving Only ns Atomic Orbitals
We begin our discussion of molecular orbitals with the simplest molecule, H2, formed from two isolated hydrogen atoms, each with a 1s1 electron configuration. As we explained in Chapter 9, electrons can behave like waves. In the molecular orbital approach, the overlapping atomic orbitals are described by mathematical equations called wave functions. The 1s atomic orbitals on the two hydrogen atoms interact to form two new molecular orbitals, one produced by taking the sum of the two H 1s wave functions, and the other produced by taking their difference:
\[ \begin{matrix}
MO(1)= & AO(atom\; A) & +& AO(atomB) \\
MO(1)= & AO(atom\; A) & -&AO(atomB)
\end{matrix} \label{9.7.1} \]
The molecular orbitals created from Equation \(\ref{9.7.1}\) are called linear combinations of atomic orbitals (LCAOs) Molecular orbitals created from the sum and the difference of two wave functions (atomic orbitals). A molecule must have as many molecular orbitals as there are atomic orbitals.
A molecule must have as many molecular orbitals as there are atomic orbitals.
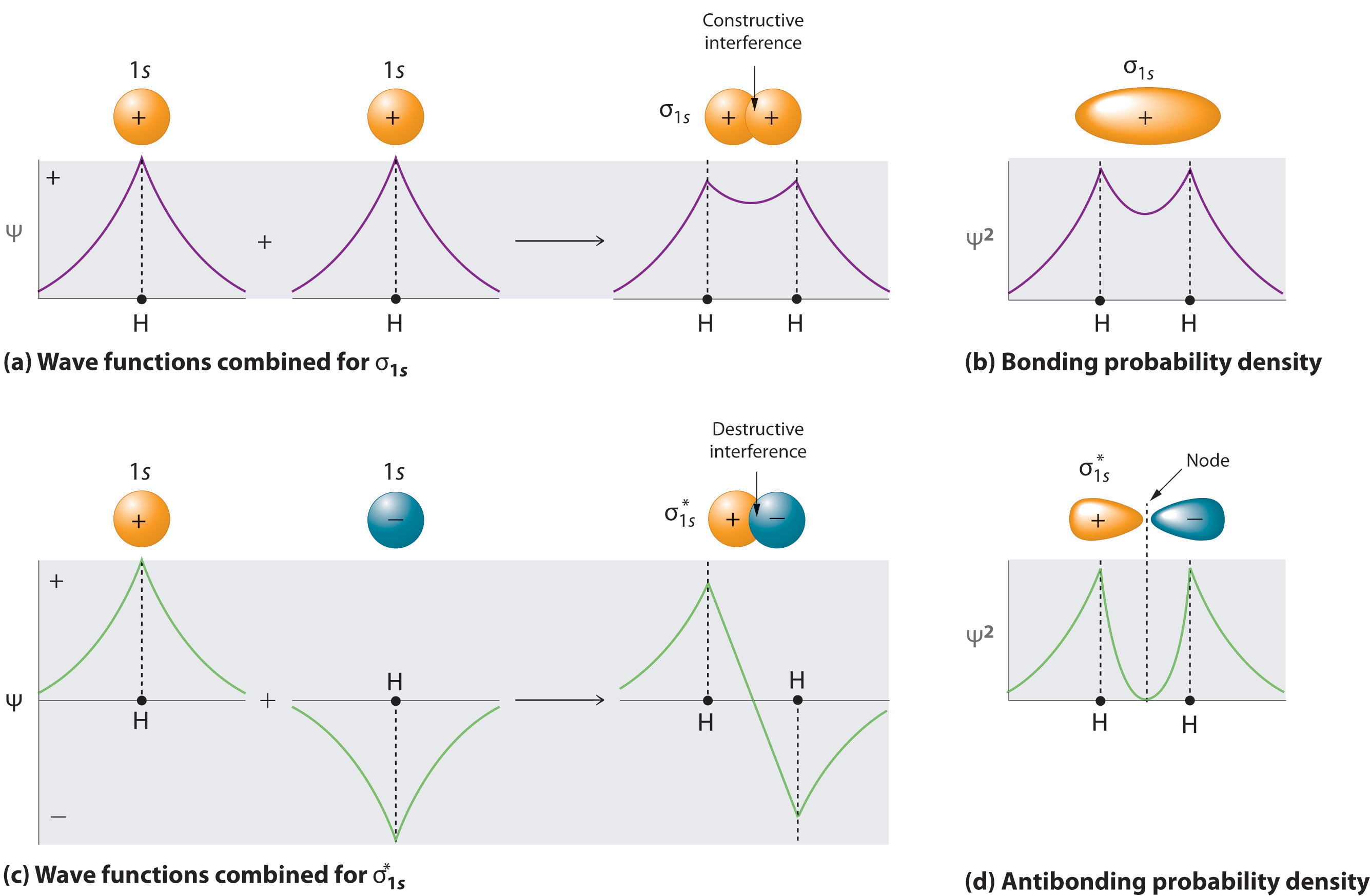
Adding two atomic orbitals corresponds to constructive interference between two waves, thus reinforcing their intensity; the internuclear electron probability density is increased. The molecular orbital corresponding to the sum of the two H 1s orbitals is called a σ1s combination (pronounced “sigma one ess”) (part (a) and part (b) in Figure \(\PageIndex{1}\)). In a sigma (σ) orbital, (i.e., a bonding molecular orbital in which the electron density along the internuclear axis and between the nuclei has cylindrical symmetry), the electron density along the internuclear axis and between the nuclei has cylindrical symmetry; that is, all cross-sections perpendicular to the internuclear axis are circles. The subscript 1s denotes the atomic orbitals from which the molecular orbital was derived: The ≈ sign is used rather than an = sign because we are ignoring certain constants that are not important to our argument.
\[ \sigma _{1s} \approx 1s\left ( A \right ) + 1s\left ( B \right ) \label{9.7.2} \]
Conversely, subtracting one atomic orbital from another corresponds to destructive interference between two waves, which reduces their intensity and causes a decrease in the internuclear electron probability density (part (c) and part (d) in Figure \(\PageIndex{1}\)). The resulting pattern contains a node where the electron density is zero. The molecular orbital corresponding to the difference is called \( \sigma _{1s}^{*} \) (“sigma one ess star”). In a sigma star (σ*) orbital An antibonding molecular orbital in which there is a region of zero electron probability (a nodal plane) perpendicular to the internuclear axis., there is a region of zero electron probability, a nodal plane, perpendicular to the internuclear axis:
\[ \sigma _{1s}^{\star } \approx 1s\left ( A \right ) - 1s\left ( B \right ) \label{9.7.3} \]
The electron density in the σ1s molecular orbital is greatest between the two positively charged nuclei, and the resulting electron–nucleus electrostatic attractions reduce repulsions between the nuclei. Thus the σ1s orbital represents a bonding molecular orbital. A molecular orbital that forms when atomic orbitals or orbital lobes with the same sign interact to give increased electron probability between the nuclei due to constructive reinforcement of the wave functions. In contrast, electrons in the \( \sigma _{1s}^{\star } \) orbital are generally found in the space outside the internuclear region. Because this allows the positively charged nuclei to repel one another, the \( \sigma _{1s}^{\star } \) orbital is an antibonding molecular orbital (a molecular orbital that forms when atomic orbitals or orbital lobes of opposite sign interact to give decreased electron probability between the nuclei due to destructive reinforcement of the wave functions).
Antibonding orbitals contain a node perpendicular to the internuclear axis; bonding orbitals do not.
Energy-Level Diagrams
Because electrons in the σ1s orbital interact simultaneously with both nuclei, they have a lower energy than electrons that interact with only one nucleus. This means that the σ1s molecular orbital has a lower energy than either of the hydrogen 1s atomic orbitals. Conversely, electrons in the \( \sigma _{1s}^{\star } \) orbital interact with only one hydrogen nucleus at a time. In addition, they are farther away from the nucleus than they were in the parent hydrogen 1s atomic orbitals. Consequently, the \( \sigma _{1s}^{\star } \) molecular orbital has a higher energy than either of the hydrogen 1s atomic orbitals. The σ1s (bonding) molecular orbital is stabilized relative to the 1s atomic orbitals, and the \( \sigma _{1s}^{\star } \) (antibonding) molecular orbital is destabilized. The relative energy levels of these orbitals are shown in the energy-level diagram (a schematic drawing that compares the energies of the molecular orbitals (bonding, antibonding, and nonbonding) with the energies of the parent atomic orbitals) in Figure \(\PageIndex{2}\)
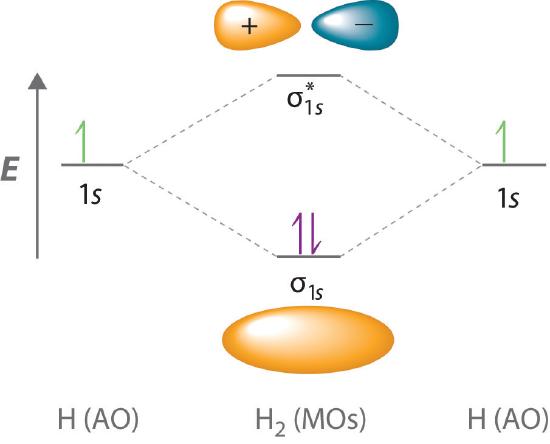
A bonding molecular orbital is always lower in energy (more stable) than the component atomic orbitals, whereas an antibonding molecular orbital is always higher in energy (less stable).
To describe the bonding in a homonuclear diatomic molecule (a molecule that consists of two atoms of the same element) such as H2, we use molecular orbitals; that is, for a molecule in which two identical atoms interact, we insert the total number of valence electrons into the energy-level diagram (Figure \(\PageIndex{2}\)). We fill the orbitals according to the Pauli principle and Hund’s rule: each orbital can accommodate a maximum of two electrons with opposite spins, and the orbitals are filled in order of increasing energy. Because each H atom contributes one valence electron, the resulting two electrons are exactly enough to fill the σ1s bonding molecular orbital. The two electrons enter an orbital whose energy is lower than that of the parent atomic orbitals, so the H2 molecule is more stable than the two isolated hydrogen atoms. Thus molecular orbital theory correctly predicts that H2 is a stable molecule. Because bonds form when electrons are concentrated in the space between nuclei, this approach is also consistent with our earlier discussion of electron-pair bonds.
Bond Order in Molecular Orbital Theory
In the Lewis electron structures, the number of electron pairs holding two atoms together was called the bond order. In the molecular orbital approach, bond order One-half the net number of bonding electrons in a molecule. is defined as one-half the net number of bonding electrons:
\[ bond\; order=\dfrac{number\; of \; bonding\; electrons-number\; of \; antibonding\; electrons}{2} \label{9.7.4} \]
To calculate the bond order of H2, we see from Figure \(\PageIndex{2}\) that the σ1s (bonding) molecular orbital contains two electrons, while the \( \sigma _{1s}^{\star } \) (antibonding) molecular orbital is empty. The bond order of H2 is therefore
\[ \dfrac{2-0}{2}=1 \label{9.7.5} \]
This result corresponds to the single covalent bond predicted by Lewis dot symbols. Thus molecular orbital theory and the Lewis electron-pair approach agree that a single bond containing two electrons has a bond order of 1. Double and triple bonds contain four or six electrons, respectively, and correspond to bond orders of 2 and 3. We can use energy-level diagrams such as the one in Figure \(\PageIndex{2}\) to describe the bonding in other pairs of atoms and ions where n = 1, such as the H2+ ion, the He2+ ion, and the He2 molecule. Again, we fill the lowest-energy molecular orbitals first while being sure not to violate the Pauli principle or Hund’s rule.

Figure \(\PageIndex{3a}\) shows the energy-level diagram for the H2+ ion, which contains two protons and only one electron. The single electron occupies the σ1s bonding molecular orbital, giving a (σ1s)1 electron configuration. The number of electrons in an orbital is indicated by a superscript. In this case, the bond order is
\[\dfrac{1-0}{2}=1/2 \nonumber \]
Because the bond order is greater than zero, the H2+ ion should be more stable than an isolated H atom and a proton. We can therefore use a molecular orbital energy-level diagram and the calculated bond order to predict the relative stability of species such as H2+. With a bond order of only 1/2 the bond in H2+ should be weaker than in the H2 molecule, and the H–H bond should be longer. As shown in Table \(\PageIndex{1}\), these predictions agree with the experimental data.
Figure \(\PageIndex{3b}\) is the molecular orbital energy-level diagram for He2+. This ion has a total of three valence electrons. Because the first two electrons completely fill the σ1s molecular orbital, the Pauli principle states that the third electron must be in the \( \sigma _{1s}^{\star} \) antibonding orbital, giving a \( \left (\sigma _{1s} \right )^{2}\left (\sigma _{1s}^{\star } \right )^{1} \) electron configuration. This electron configuration gives a bond order of
\[\dfrac{2-1}{2}=1/2 \nonumber \]
As with H2+, the He2+ ion should be stable, but the He–He bond should be weaker and longer than in H2. In fact, the He2+ ion can be prepared, and its properties are consistent with our predictions (Table \(\PageIndex{1}\)).
| Molecule or Ion | Electron Configuration | Bond Order | Bond Length (pm) | Bond Energy (kJ/mol) |
|---|---|---|---|---|
| H2+ | (σ1s)1 | 1/2 | 106 | 269 |
| H2 | (σ1s)2 | 1 | 74 | 436 |
| He2+ | \( \left (\sigma _{1s} \right )^{2}\left (\sigma _{1s}^{\star } \right )^{1} \) | 1/2 | 108 | 251 |
| He2 | \( \left (\sigma _{1s} \right )^{2}\left (\sigma _{1s}^{\star } \right )^{2} \) | 0 | not observed | not observed |
Finally, we examine the He2 molecule, formed from two He atoms with 1s2 electron configurations. Figure \(\PageIndex{3c}\) is the molecular orbital energy-level diagram for He2. With a total of four valence electrons, both the σ1s bonding and \( \sigma _{1s}^{\star } \) antibonding orbitals must contain two electrons. This gives a \( \left (\sigma _{1s} \right )^{2}\left (\sigma _{1s}^{\star } \right )^{2} \) electron configuration, with a predicted bond order of (2 − 2) ÷ 2 = 0, which indicates that the He2 molecule has no net bond and is not a stable species. Experiments show that the He2 molecule is actually less stable than two isolated He atoms due to unfavorable electron–electron and nucleus–nucleus interactions.
In molecular orbital theory, electrons in antibonding orbitals effectively cancel the stabilization resulting from electrons in bonding orbitals. Consequently, any system that has equal numbers of bonding and antibonding electrons will have a bond order of 0, and it is predicted to be unstable and therefore not to exist in nature. In contrast to Lewis electron structures and the valence bond approach, molecular orbital theory is able to accommodate systems with an odd number of electrons, such as the H2+ ion.
In contrast to Lewis electron structures and the valence bond approach, molecular orbital theory can accommodate systems with an odd number of electrons.
Use a molecular orbital energy-level diagram, such as those in Figure \(\PageIndex{2}\), to predict the bond order in the He22+ ion. Is this a stable species?
Given: chemical species
Asked for: molecular orbital energy-level diagram, bond order, and stability
Strategy:
- Combine the two He valence atomic orbitals to produce bonding and antibonding molecular orbital
- s. Draw the molecular orbital energy-level diagram for the system.
- Determine the total number of valence electrons in the He22+ ion. Fill the molecular orbitals in the energy-level diagram beginning with the orbital with the lowest energy. Be sure to obey the Pauli principle and Hund’s rule while doing so.
- Calculate the bond order and predict whether the species is stable.
Solution:
A Two He 1s atomic orbitals combine to give two molecular orbitals: a σ1s bonding orbital at lower energy than the atomic orbitals and a \( \sigma _{1s}^{\star } \) antibonding orbital at higher energy. The bonding in any diatomic molecule with two He atoms can be described using the following molecular orbital diagram:
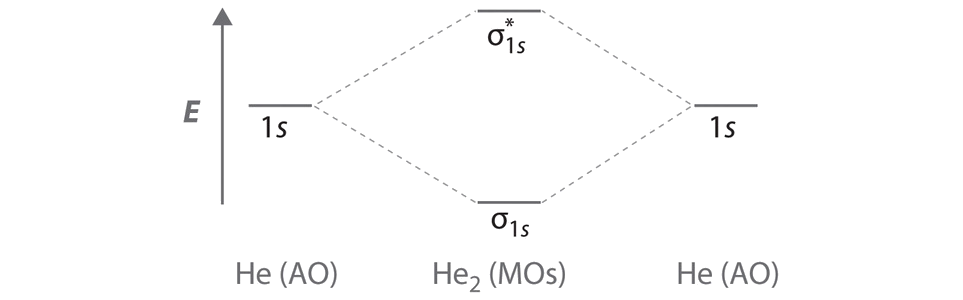
B The He22+ ion has only two valence electrons (two from each He atom minus two for the +2 charge). We can also view He22+ as being formed from two He+ ions, each of which has a single valence electron in the 1s atomic orbital. We can now fill the molecular orbital diagram:
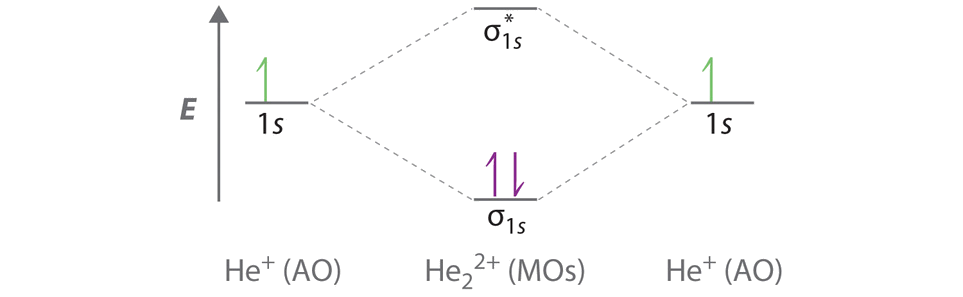
The two electrons occupy the lowest-energy molecular orbital, which is the bonding (σ1s) orbital, giving a (σ1s)2 electron configuration. To avoid violating the Pauli principle, the electron spins must be paired. C So the bond order is
\[ \dfrac{2-0}{2} =1 \nonumber \]
He22+ is therefore predicted to contain a single He–He bond. Thus it should be a stable species.
Use a molecular orbital energy-level diagram to predict the valence-electron configuration and bond order of the H22− ion. Is this a stable species?
- Answer
-
H22− has a valence electron configuration of \( \left (\sigma _{1s} \right )^{2}\left (\sigma _{1s}^{\star } \right )^{2} \) with a bond order of 0. It is therefore predicted to be unstable.
So far, our discussion of molecular orbitals has been confined to the interaction of valence orbitals, which tend to lie farthest from the nucleus. When two atoms are close enough for their valence orbitals to overlap significantly, the filled inner electron shells are largely unperturbed; hence they do not need to be considered in a molecular orbital scheme. Also, when the inner orbitals are completely filled, they contain exactly enough electrons to completely fill both the bonding and antibonding molecular orbitals that arise from their interaction. Thus the interaction of filled shells always gives a bond order of 0, so filled shells are not a factor when predicting the stability of a species. This means that we can focus our attention on the molecular orbitals derived from valence atomic orbitals.
A molecular orbital diagram that can be applied to any homonuclear diatomic molecule with two identical alkali metal atoms (Li2 and Cs2, for example) is shown in part (a) in Figure \(\PageIndex{4}\), where M represents the metal atom. Only two energy levels are important for describing the valence electron molecular orbitals of these species: a σns bonding molecular orbital and a σ*ns antibonding molecular orbital. Because each alkali metal (M) has an ns1 valence electron configuration, the M2 molecule has two valence electrons that fill the σns bonding orbital. As a result, a bond order of 1 is predicted for all homonuclear diatomic species formed from the alkali metals (Li2, Na2, K2, Rb2, and Cs2). The general features of these M2 diagrams are identical to the diagram for the H2 molecule in Figure \(\PageIndex{4}\). Experimentally, all are found to be stable in the gas phase, and some are even stable in solution.
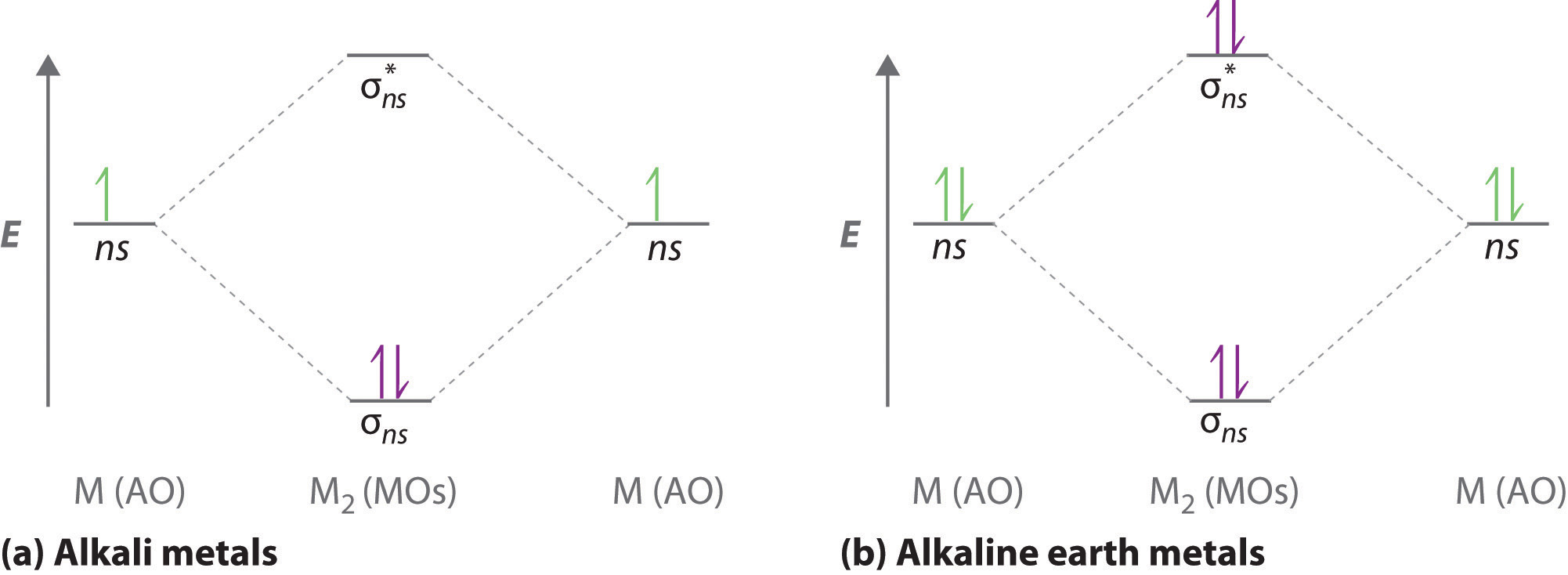
Similarly, the molecular orbital diagrams for homonuclear diatomic compounds of the alkaline earth metals (such as Be2), in which each metal atom has an ns2 valence electron configuration, resemble the diagram for the He2 molecule in part (c) in Figure \(\PageIndex{2}\). As shown in part (b) in Figure \(\PageIndex{4}\), this is indeed the case. All the homonuclear alkaline earth diatomic molecules have four valence electrons, which fill both the σns bonding orbital and the σns* antibonding orbital and give a bond order of 0. Thus Be2, Mg2, Ca2, Sr2, and Ba2 are all expected to be unstable, in agreement with experimental data.In the solid state, however, all the alkali metals and the alkaline earth metals exist as extended lattices held together by metallic bonding. At low temperatures, \(Be_2\) is stable.
Use a qualitative molecular orbital energy-level diagram to predict the valence electron configuration, bond order, and likely existence of the Na2− ion.
Given: chemical species
Asked for: molecular orbital energy-level diagram, valence electron configuration, bond order, and stability
Strategy:
- Combine the two sodium valence atomic orbitals to produce bonding and antibonding molecular orbitals. Draw the molecular orbital energy-level diagram for this system.
- Determine the total number of valence electrons in the Na2− ion. Fill the molecular orbitals in the energy-level diagram beginning with the orbital with the lowest energy. Be sure to obey the Pauli principle and Hund’s rule while doing so.
- Calculate the bond order and predict whether the species is stable.
Solution:
A Because sodium has a [Ne]3s1 electron configuration, the molecular orbital energy-level diagram is qualitatively identical to the diagram for the interaction of two 1s atomic orbitals. B The Na2− ion has a total of three valence electrons (one from each Na atom and one for the negative charge), resulting in a filled σ3s molecular orbital, a half-filled σ3s* and a \( \left ( \sigma _{3s} \right )^{2}\left ( \sigma _{3s}^{\star } \right )^{1} \) electron configuration.
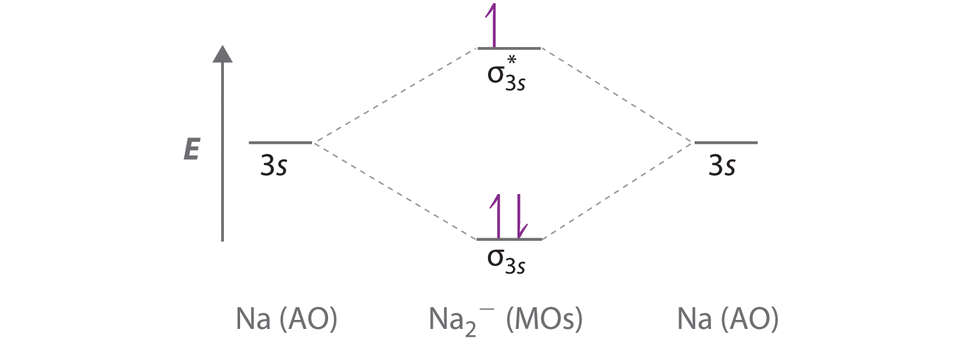
C The bond order is (2-1)÷2=1/2 With a fractional bond order, we predict that the Na2− ion exists but is highly reactive.
Use a qualitative molecular orbital energy-level diagram to predict the valence electron configuration, bond order, and likely existence of the Ca2+ ion.
- Answer
-
Ca2+ has a \( \left ( \sigma _{4s} \right )^{2}\left ( \sigma _{4s}^{\star } \right )^{1} \) electron configurations and a bond order of 1/2 and should exist.
Molecular Orbitals Formed from ns and np Atomic Orbitals
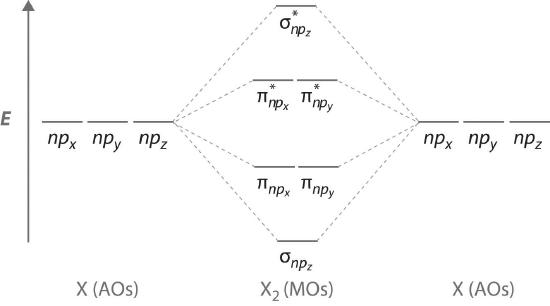
Atomic orbitals other than ns orbitals can also interact to form molecular orbitals. Because individual p, d, and f orbitals are not spherically symmetrical, however, we need to define a coordinate system so we know which lobes are interacting in three-dimensional space. Recall that for each np subshell, for example, there are npx, npy, and npz orbitals. All have the same energy and are therefore degenerate, but they have different spatial orientations.
\[ \sigma _{np_{z}}=np_{z}\left ( A \right )-np_{z}\left ( B \right ) \label{9.7.6} \]
Just as with ns orbitals, we can form molecular orbitals from np orbitals by taking their mathematical sum and difference. When two positive lobes with the appropriate spatial orientation overlap, as illustrated for two npz atomic orbitals in part (a) in Figure \(\PageIndex{5}\), it is the mathematical difference of their wave functions that results in constructive interference, which in turn increases the electron probability density between the two atoms. The difference therefore corresponds to a molecular orbital called a \( \sigma _{np_{z}} \) bonding molecular orbital because, just as with the σ orbitals discussed previously, it is symmetrical about the internuclear axis (in this case, the z-axis):
\[ \sigma _{np_{z}}=np_{z}\left ( A \right )-np_{z}\left ( B \right ) \label{9.7.7A} \]
The other possible combination of the two npz orbitals is the mathematical sum:
\[ \sigma _{np_{z}}=np_{z}\left ( A \right )+np_{z}\left ( B \right ) \label{9.7.7} \]
In this combination, shown in part (b) in Figure \(\PageIndex{5}\), the positive lobe of one npz atomic orbital overlaps the negative lobe of the other, leading to destructive interference of the two waves and creating a node between the two atoms. Hence this is an antibonding molecular orbital. Because it, too, is symmetrical about the internuclear axis, this molecular orbital is called a \( \sigma _{np_{z}}=np_{z}\left ( A \right )-np_{z}\left ( B \right ) \) antibonding molecular orbital. Whenever orbitals combine, the bonding combination is always lower in energy (more stable) than the atomic orbitals from which it was derived, and the antibonding combination is higher in energy (less stable).
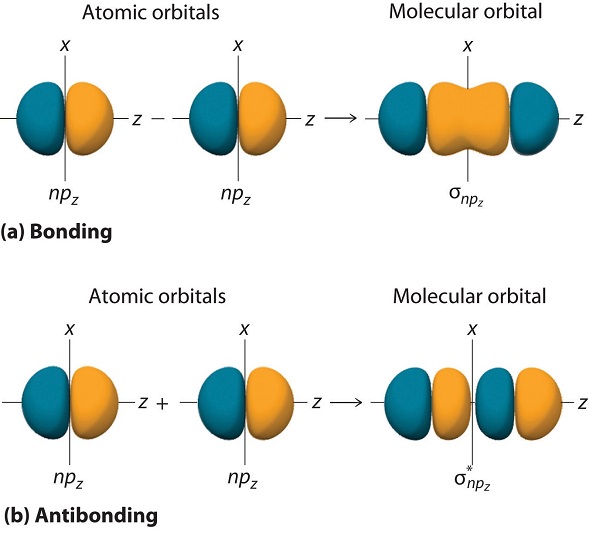
Overlap of atomic orbital lobes with the same sign produces a bonding molecular orbital, regardless of whether it corresponds to the sum or the difference of the atomic orbitals.
The remaining p orbitals on each of the two atoms, npx and npy, do not point directly toward each other. Instead, they are perpendicular to the internuclear axis. If we arbitrarily label the axes as shown in Figure \(\PageIndex{6}\), we see that we have two pairs of np orbitals: the two npx orbitals lying in the plane of the page, and two npy orbitals perpendicular to the plane. Although these two pairs are equivalent in energy, the npx orbital on one atom can interact with only the npx orbital on the other, and the npy orbital on one atom can interact with only the npy on the other. These interactions are side-to-side rather than the head-to-head interactions characteristic of σ orbitals. Each pair of overlapping atomic orbitals again forms two molecular orbitals: one corresponds to the arithmetic sum of the two atomic orbitals and one to the difference. The sum of these side-to-side interactions increases the electron probability in the region above and below a line connecting the nuclei, so it is a bonding molecular orbital that is called a pi (π) orbital (a bonding molecular orbital formed from the side-to-side interactions of two or more parallel np atomic orbitals). The difference results in the overlap of orbital lobes with opposite signs, which produces a nodal plane perpendicular to the internuclear axis; hence it is an antibonding molecular orbital, called a pi star (π*) orbital An antibonding molecular orbital formed from the difference of the side-to-side interactions of two or more parallel np atomic orbitals, creating a nodal plane perpendicular to the internuclear axis..
\[ \pi _{np_{x}}=np_{x}\left ( A \right )+np_{x}\left ( B \right ) \label{9.7.8} \]
\[ \pi ^{\star }_{np_{x}}=np_{x}\left ( A \right )-np_{x}\left ( B \right ) \label{9.7.9} \]
The two npy orbitals can also combine using side-to-side interactions to produce a bonding \( \pi _{np_{y}} \) molecular orbital and an antibonding \( \pi _{np_{y}}^{\star } \) molecular orbital. Because the npx and npy atomic orbitals interact in the same way (side-to-side) and have the same energy, the \( \pi _{np_{x}} \) and \( \pi _{np_{y}} \)molecular orbitals are a degenerate pair, as are the \( \pi _{np_{x}}^{\star } \) and \( \pi _{np_{y}}^{\star } \) molecular orbitals.
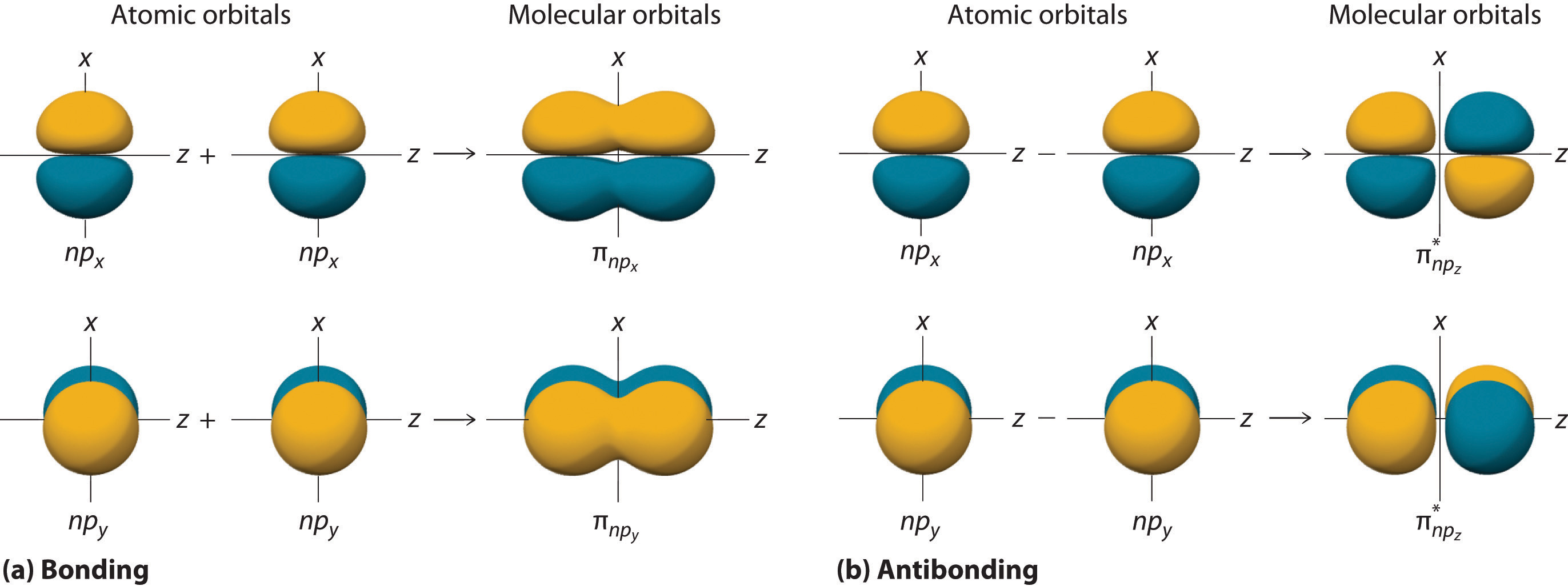
Figure \(\PageIndex{7}\) is an energy-level diagram that can be applied to two identical interacting atoms that have three np atomic orbitals each. There are six degenerate p atomic orbitals (three from each atom) that combine to form six molecular orbitals, three bonding and three antibonding. The bonding molecular orbitals are lower in energy than the atomic orbitals because of the increased stability associated with the formation of a bond. Conversely, the antibonding molecular orbitals are higher in energy, as shown. The energy difference between the σ and σ* molecular orbitals is significantly greater than the difference between the two π and π* sets. The reason for this is that the atomic orbital overlap and thus the strength of the interaction are greater for a σ bond than a π bond, which means that the σ molecular orbital is more stable (lower in energy) than the π molecular orbitals.
Although many combinations of atomic orbitals form molecular orbitals, we will discuss only one other interaction: an ns atomic orbital on one atom with an npz atomic orbital on another. As shown in Figure \(\PageIndex{8}\), the sum of the two atomic wave functions (ns + npz) produces a σ bonding molecular orbital. Their difference (ns − npz) produces a σ* antibonding molecular orbital, which has a nodal plane of zero probability density perpendicular to the internuclear axis.

Summary
Molecular orbital theory, a delocalized approach to bonding, can often explain a compound’s color, why a compound with unpaired electrons is stable, semiconductor behavior, and resonance, none of which can be explained using a localized approach. A molecular orbital (MO) is an allowed spatial distribution of electrons in a molecule that is associated with a particular orbital energy. Unlike an atomic orbital (AO), which is centered on a single atom, a molecular orbital extends over all the atoms in a molecule or ion. Hence the molecular orbital theory of bonding is a delocalized approach. Molecular orbitals are constructed using linear combinations of atomic orbitals (LCAOs), which are usually the mathematical sums and differences of wave functions that describe overlapping atomic orbitals. Atomic orbitals interact to form three types of molecular orbitals.
A completely bonding molecular orbital contains no nodes (regions of zero electron probability) perpendicular to the internuclear axis, whereas a completely antibonding molecular orbital contains at least one node perpendicular to the internuclear axis. A sigma (σ) orbital (bonding) or a sigma star (σ*) orbital (antibonding) is symmetrical about the internuclear axis. Hence all cross-sections perpendicular to that axis are circular. Both a pi (π) orbital (bonding) and a pi star (π*) orbital (antibonding) possess a nodal plane that contains the nuclei, with electron density localized on both sides of the plane.
The energies of the molecular orbitals versus those of the parent atomic orbitals can be shown schematically in an energy-level diagram. The electron configuration of a molecule is shown by placing the correct number of electrons in the appropriate energy-level diagram, starting with the lowest-energy orbital and obeying the Pauli principle; that is, placing only two electrons with opposite spin in each orbital. From the completed energy-level diagram, we can calculate the bond order, defined as one-half the net number of bonding electrons. In bond orders, electrons in antibonding molecular orbitals cancel electrons in bonding molecular orbitals, while electrons in nonbonding orbitals have no effect and are not counted. Bond orders of 1, 2, and 3 correspond to single, double, and triple bonds, respectively. Molecules with predicted bond orders of 0 are generally less stable than the isolated atoms and do not normally exist.
Contributors and Attributions
Modified by Joshua Halpern (Howard University)
- Orbitals or orbital lobes with the same sign interact to give increased electron probability along the plane of the internuclear axis because of constructive reinforcement of the wave functions. Consequently, electrons in such molecular orbitals help to hold the positively charged nuclei together. Such orbitals are bonding molecular orbitals, and they are always lower in energy than the parent atomic orbitals.
- Orbitals or orbital lobes with opposite signs interact to give decreased electron probability density between the nuclei because of destructive interference of the wave functions. Consequently, electrons in such molecular orbitals are primarily located outside the internuclear region, leading to increased repulsions between the positively charged nuclei. These orbitals are called antibonding molecular orbitals, and they are always higher in energy than the parent atomic orbitals.
- Some atomic orbitals interact only very weakly, and the resulting molecular orbitals give essentially no change in the electron probability density between the nuclei. Hence electrons in such orbitals have no effect on the bonding in a molecule or ion. These orbitals are nonbonding molecular orbitals, and they have approximately the same energy as the parent atomic orbitals.

