Chapter 7.4: Stoichiometry
- Page ID
- 18857
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
Learning Objectives
- To calculate the quantities of compounds produced or consumed in a chemical reaction.
A balanced chemical equation gives the identity of the reactants and the products as well as the accurate number of molecules or moles of each that are consumed or produced. Stoichiometry is a collective term for the quantitative relationships between the masses, the numbers of moles, and the numbers of particles (atoms, molecules, and ions) of the reactants and the products in a balanced chemical equation. A stoichiometric quantity is the amount of product or reactant specified by the coefficients in a balanced chemical equation. In Section 7.3 , for example, you learned how to express the stoichiometry of the reaction for the ammonium dichromate volcano in terms of the atoms, ions, or molecules involved and the numbers of moles, grams, and formula units of each (recognizing, for instance, that 1 mol of ammonium dichromate produces 4 mol of water). This section describes how to use the stoichiometry of a reaction to answer questions like the following: How much oxygen is needed to ensure complete combustion of a given amount of isooctane? (This information is crucial to the design of nonpolluting and efficient automobile engines.) How many grams of pure gold can be obtained from a ton of low-grade gold ore? (The answer determines whether the ore deposit is worth mining.) If an industrial plant must produce a certain number of tons of sulfuric acid per week, how much elemental sulfur must arrive by rail each week?
All these questions can be answered using the concepts of the mole and molar and formula masses, along with the coefficients in the appropriate balanced chemical equation.
Stoichiometry Problems
When we carry out a reaction in either an industrial setting or a laboratory, it is easier to work with masses of substances than with the numbers of molecules or moles. The general method for converting from the mass of any reactant or product to the mass of any other reactant or product using a balanced chemical equation is outlined in Figure 7.4.1 and described in the following text.
Steps in Converting between Masses of Reactant and Product
- Convert the mass of one substance (substance A) to the corresponding number of moles using its molar mass.
- From the balanced chemical equation, obtain the number of moles of another substance (B) from the number of moles of substance A using the appropriate mole ratio (the ratio of their coefficients).
- Convert the number of moles of substance B to mass using its molar mass. It is important to remember that some species are in excess by virtue of the reaction conditions. For example, if a substance reacts with the oxygen in air, then oxygen is in obvious (but unstated) excess.
Converting amounts of substances to moles—and vice versa—is the key to all stoichiometry problems, whether the amounts are given in units of mass (grams or kilograms), weight (pounds or tons), or volume (liters or gallons).
Figure 7.4.1 A Flowchart for Stoichiometric Calculations Involving Pure Substances

The molar masses of the reactants and the products are used as conversion factors so that you can calculate the mass of product from the mass of reactant and vice versa.
To illustrate this procedure, let’s return to the combustion of glucose. We saw earlier that glucose reacts with oxygen to produce carbon dioxide and water:
\[{C_6}{H_{12}}{O_6}\left( s \right) + 6{O_2}\left( g \right){\text{ }} \to 6C{O_2}\left( g \right) + 6{H_2}O\left( l \right) \tag{7.4.1} \]
Just before a chemistry exam, suppose a friend reminds you that glucose is the major fuel used by the human brain. You therefore decide to eat a candy bar to make sure that your brain doesn’t run out of energy during the exam (even though there is no direct evidence that consumption of candy bars improves performance on chemistry exams). If a typical 2 oz candy bar contains the equivalent of 45.3 g of glucose and the glucose is completely converted to carbon dioxide during the exam, how many grams of carbon dioxide will you produce and exhale into the exam room?
The initial step in solving a problem of this type must be to write the balanced chemical equation for the reaction. Inspection of Equation 7.4.1 shows that it is balanced as written, so we can proceed to the strategy outlined in Figure 7.4.1, adapting it as follows:
-
Use the molar mass of glucose (to one decimal place, 180.2 g/mol) to determine the number of moles of glucose in the candy bar:
\( moles\; glucose=45.3\cancel{g\; glucose}\times \dfrac{1\; mol\; glucose}{180.2\; \cancel{g\; glucose}}=0.251\; mol\; glucose \) -
According to the balanced chemical equation, 6 mol of CO2 is produced per mole of glucose; the mole ratio of CO2 to glucose is therefore 6:1. If we divide the number of moles of CO2 by its stoichiometric coefficient 6 and the number of moles of glucose by its stoichiometric coefficient of one the ratios, which can be called the reaction equivalents, are equal. (Step 2a) We will use this below in demonstrating another method of solving stoichiometric problems of all types
\( \dfrac{moles\; CO_{2}}{6\; mol\; CO_{2}} =\dfrac{moles\; glucose}{1\; mol\; glucose} \)
The number of moles of CO2 produced is thus
\( \begin{matrix}
moles CO_{2} & = & mol\; glucose\; \times \dfrac{6\; mol\; CO_{2}}{1\; mol\; glucose}\\
& & \\
& = & 0.251\; \cancel{mol\; glucose} \times \dfrac{6\; mol\; CO_{2}}{1\; \cancel{mol\; glucose}}\\
& & \\
& = & 1.51\; mol\; CO_{2}
\end{matrix} \)
3. Use the molar mass of CO2 (44.010 g/mol) to calculate the mass of CO2 corresponding to 1.51 mol of CO2:
\( mass\; of\; CO_{2}=1.51\; \cancel{mol\; CO_{2}}\times \dfrac{44.010\; g\; CO_{2}}{1\; \cancel{mol\; CO_{2}}}=66.5\; g\; CO_{2} \)
4 We can summarize these operations as follows:
\( \begin{matrix}
45.3\; g\; glucose & \times \dfrac{1\; mol\; glucose}{180.2\; g\; glucose} & \times \dfrac{6\; mol\; CO_{2}}{1\; mol\; glucose} & \times \dfrac{44.010\; g\; CO_{2}}{1\; mol\; CO_{2}} &=66.4\; g\; CO_{2} \\
& step\; 1 & step\; 2 & step\; 3 &
\end{matrix} \)
Discrepancies between the two values are attributed to rounding errors resulting from using stepwise calculations in steps 1–3. (For more information about rounding and significant digits. (See Essential Skills 1 in Section 1.8 ) In Chapter 9, you will discover that this amount of gaseous carbon dioxide occupies an enormous volume—more than 33 L. We could use similar methods to calculate the amount of oxygen consumed or the amount of water produced.
We just used the balanced chemical equation to calculate the mass of product that is formed from a certain amount of reactant. We can also use the balanced chemical equation to determine the masses of reactants that are necessary to form a certain amount of product or, as shown in Example 11, the mass of one reactant that is required to consume a given mass of another reactant.
There is another way of dealing with such problems which is easier to carry out. It starts by writing the balanced chemical equation and then drawing a table with five rows and as many columns as there are reactants and products and writing in the Mass of the given reactant
| C6H12O6(s) | + 6O2(g) | → 6CO2(g) | + 6H2O(l) | |
| Mass (g) | 45.3 | |||
| Molecular Weight (g/mol) | ||||
| Moles | ||||
| Stoichiometric Coefficients | ||||
| Stoichiometric Equivalents |
We then simply fill in the stoichiometric coefficients and the molecular weights of the reactants and the products that we are concerned with
| C6H12O6(s) | + 6O2(g) | → 6CO2(g) | + 6H2O(l) | |
| Mass (g) | 45.3 | |||
| Molecular Weight (g/mol) | 180.2 | |||
| Moles | ||||
| Stoichiometric Coefficients |
1 | 6 | ||
| Stoichiometric Equivalents |
Then divide the mass of the glucose by the molecular weight to find the number of moles of glucose. In the next step divide the number of moles by the stoichiometric coefficient to find the stoichiometric equivalents (this is the same as step 2a above. The rule is to divide going down the table. You divide the Mass by the Molecular Weight to find the number of Moles, you divide the number of Moles by the Stoichiometric Coefficients to find the number of Stoichiometric Equivalents
| C6H12O6(s) | + 6O2(g) | → 6CO2(g) | + 6H2O(l) | |
| Mass (g) | 45.3 | |||
| Molecular Weight (g/mol) | 180.2 | |||
| Moles | 0.251 | |||
| Stoichiometric Coefficients |
1 | 6 | ||
| Stoichiometric Equivalents |
0.251 |
For each of the products and reactants, the Stoichiometric Equivalents will be the same (they are equivalent, simply copy across).
| C6H12O6(s) | + 6O2(g) | → 6CO2(g) | + 6H2O(l) | |
| Mass (g) | 45.3 | 66.4 | ||
| Molecular Weight (g/mol) | 180.2 | 44.01 | ||
| Moles | 0.251 | 1.51 | ||
| Stoichiometric Coefficients |
1 | 6 | ||
| Stoichiometric Equivalents |
0.251 | 0.251 |
Now multiply going up. Multiply the Stoichiometric Equivalents by the Stoichiometric Coefficient to find the number of Moles of CO2 then multiply the number of Moles of CO2 by the Molecular Weight of CO2 to find the Mass of CO2 produced in the reaction. Close inspection of both methods will show that they are equivalent. The table has the advantage that it is a "fill in the spaces" exercise, and practically automatic. In fact you could easily write an Excel spreadsheet to do it. The table method has advantages if we want to answer question such as how much water will be produced or how much oxygen will be consumed. It also is simpler for more complicated limiting reagent problems.
As an example, we can now figure out how much oxygen is used up and how much water will be produced by this reaction. Simply use the same method as for the CO2.
| C6H12O6(s) | + 6O2(g) | → 6CO2(g) | + 6H2O(l) | |
| Mass (g) | 45.3 | 48.32 | 66.4 | 27.2 |
| Molecular Weight (g/mol) | 180.2 | 32.00 | 44.01 | 18.02 |
| Moles | 0.251 | 1.51 | 1.51 | 1.51 |
| Stoichiometric Coefficients |
1 | 6 | 6 | 6 |
| Stoichiometric Equivalents |
0.251 | 0.251 | 0.251 | 0.251 |
Notice that all of the Stoichiometric Equivalents are the same and that we multiply the Stoichiometric Equivalents by the Stoichiometric Coefficients to find the number of Moles, and the number of Moles by the Molecular Weight to find the Mass.
Example 11
The combustion of hydrogen with oxygen to produce gaseous water is extremely vigorous, producing one of the hottest flames known. Because so much energy is released for a given mass of hydrogen or oxygen, this reaction was used to fuel the NASA (National Aeronautics and Space Administration) space shuttles, which have recently been retired from service. NASA engineers calculated the exact amount of each reactant needed for the flight to make sure that the shuttles did not carry excess fuel into orbit. Calculate how many tons of hydrogen a space shuttle needed to carry for each 1.00 tn of oxygen (1 tn = 2000 lb).

The US space shuttle Discovery during liftoff. The large cylinder in the middle contains the oxygen and hydrogen that fueled the shuttle’s main engine.
Given: reactants, products, and mass of one reactant
Asked for: mass of other reactant
Strategy:
A Write the balanced chemical equation for the reaction.
B Convert mass of oxygen to moles. From the mole ratio in the balanced chemical equation, determine the number of moles of hydrogen required. Then convert the moles of hydrogen to the equivalent mass in tons.
Solution:
We use the same general strategy for solving stoichiometric calculations as in the preceding example. Because the amount of oxygen is given in tons rather than grams, however, we also need to convert tons to units of mass in grams. Another conversion is needed at the end to report the final answer in tons.
A We first use the information given to write a balanced chemical equation. Because we know the identity of both the reactants and the product, we can write the reaction as follows:
\[{H_2}\left( g \right) + {O_2}\left( g \right){\text{ }} \to {H_2}O\left( g \right) \notag \]
This equation is not balanced because there are two oxygen atoms on the left side and only one on the right. Assigning a coefficient of 2 to both H2O and H2 gives the balanced chemical equation:
\[2{H_2}\left( g \right) + {O_2}\left( g \right){\text{ }} \to 2{H_2}O\left( g \right) \notag \]
Thus 2 mol of H2 react with 1 mol of O2 to produce 2 mol of H2O.
B To convert tons of oxygen to units of mass in grams, we multiply by the appropriate conversion factors:
\( mass\; of\; O_{2}=1.0\; \cancel{tn} \times \dfrac{2000\; \cancel{lb}}{\cancel{tn}}\times \dfrac{4453.6\; g}{\cancel{lb}}= 9.07\times 10^{5}\; g\; O_{2} \notag \)
Using the molar mass of O2 (32.00 g/mol to four significant figures) we can calculate the number of moles of O2 contained in this mass of O2
\( mol\; O_{2}=9.07\times 10^{5}\; \cancel{g\; O_{2}} \times \dfrac{1\; mol\; O_{2}}{32.00\; \cancel{g\; O_{2}}}= 2.83\times 10^{4}\; mol\; O_{2} \notag \)
-
Now use the coefficients in the balanced chemical equation to obtain the number of moles of H2 needed to react with this number of moles of O2:
-
The molar mass of H2 (2.016 g/mol) allows us to calculate the corresponding mass of H2:
Finally, convert the mass of H2 to the desired units (tons) by using the appropriate conversion factors:
The space shuttle had to be designed to carry 0.126 tn of H2 for each 1.00 tn of O2. Even though 2 mol of H2 are needed to react with each mole of O2, the molar mass of H2 is so much smaller than that of O2 that only a relatively small mass of H2 is needed compared to the mass of O2.
Exercise
Alchemists produced elemental mercury by roasting the mercury-containing ore cinnabar (HgS) in air:
\[HgS\left( s \right) + {O_2}\left( g \right){\text{ }} \to {\text{ }}Hg\left( l \right) + S{O_2}\left( g \right) \notag \]
The volatility and toxicity of mercury make this a hazardous procedure, which likely shortened the life span of many alchemists. Given 100 g of cinnabar, how much elemental mercury can be produced from this reaction?
Answer: 86.2 g
Limiting Reactants
In all the examples discussed thus far, the reactants were assumed to be present in stoichiometric quantities. Consequently, none of the reactants was left over at the end of the reaction. This is often desirable, as in the case of a space shuttle, where excess oxygen or hydrogen was not only extra freight to be hauled into orbit but also an explosion hazard. More often, however, reactants are present in mole ratios that are not the same as the ratio of the coefficients in the balanced chemical equation. As a result, one or more of them will not be used up completely but will be left over when the reaction is completed. In this situation, the amount of product that can be obtained is limited by the amount of only one of the reactants. The reactant that restricts the amount of product obtained is called the limiting reactant. The reactant that remains after a reaction has gone to completion is in excess.
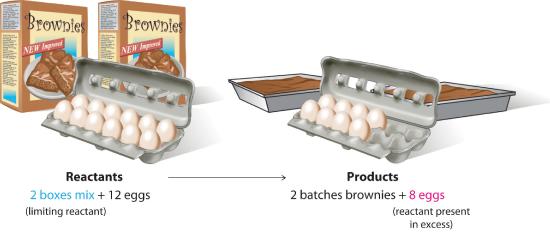
To be certain you understand these concepts, let’s first consider a nonchemical example. Assume you have invited some friends for dinner and want to bake brownies for dessert. You find two boxes of brownie mix in your pantry and see that each package requires two eggs. The balanced equation for brownie preparation is thus
\[1{\text{ }}box{\text{ }}mix + 2{\text{ }}eggs{\text{ }} \to {\text{ }}1{\text{ }}batch{\text{ }}brownies \tag{7.4.2}\]
If you have a dozen eggs, which ingredient will determine the number of batches of brownies that you can prepare? Because each box of brownie mix requires two eggs and you have two boxes, you need four eggs. Twelve eggs is eight more eggs than you need. Although the ratio of eggs to boxes in Equation 7.4.2 is 2:1, the ratio in your possession is 6:1. Hence the eggs are the ingredient (reactant) present in excess, and the brownie mix is the limiting reactant (Figure 7.4.2). Even if you had a refrigerator full of eggs, you could make only two batches of brownies.
Figure 7.4.2 The Concept of a Limiting Reactant in the Preparation of Brownies
Let’s now turn to a chemical example of a limiting reactant: the production of pure titanium. This metal is fairly light (45% lighter than steel and only 60% heavier than aluminum) and has great mechanical strength (as strong as steel and twice as strong as aluminum). Because it is also highly resistant to corrosion and can withstand extreme temperatures, titanium has many applications in the aerospace industry. Titanium is also used in medical implants and portable computer housings because it is light and resistant to corrosion. Although titanium is the ninth most common element in Earth’s crust, it is relatively difficult to extract from its ores. In the first step of the extraction process, titanium-containing oxide minerals react with solid carbon and chlorine gas to form titanium tetrachloride (TiCl4) and carbon dioxide. Titanium tetrachloride is then converted to metallic titanium by reaction with magnesium metal at high temperature:
\[TiC{l_4}\left( g \right) + 2Mg\left( l \right){\text{ }} \to {\text{ }}Ti\left( s \right) + 2MgC{l_2}\left( l \right) \tag{7.4.3}\]
Because titanium ores, carbon, and chlorine are all rather inexpensive, the high price of titanium (about $100 per kilogram) is largely due to the high cost of magnesium metal. Under these circumstances economically one would want to maximize the use of magnesium making sure that none was left during the production of titanium metal. If a little bit of the titanium (IV) chloride were left over that would not be so concerning.

Medical use of titanium. Here is an example of its successful use in joint replacement implants.
Suppose you have 1.00 kg of titanium tetrachloride and 200 g of magnesium metal. How much titanium metal can you produce according to Equation 7.4.3? Solving this type of problem requires that you carry out the following steps:
- Determine the number of moles of each reactant.
- Compare the mole ratio of the reactants with the ratio in the balanced chemical equation to determine which reactant is limiting.
- Calculate the number of moles of product that can be obtained from the limiting reactant.
- Convert the number of moles of product to mass of product.
-
To determine the number of moles of reactants present, you must calculate or look up their molar masses: 189.679 g/mol for titanium tetrachloride and 24.305 g/mol for magnesium. The number of moles of each is calculated as follows:
\[ \begin{matrix}
moles TiCl_{4} &=\dfrac{mass\; TiCl_{4}}{molar\; mass\; TiCl_{4}} \\
& \\
&=1000\; \cancel{g\; TiCl_{4}}\times \dfrac{1\; mol\; TiCl_{4}}{189.679\; \cancel{g\; TiCl_{4}}}=5.272\; mol\; TiCl_{4} \\
& \\
moles Mg &=\dfrac{mass\; Mg}{molar\; mass\; Mg} \\
& \\
&=200\;\cancel{g\;Mg} \times \dfrac{1\; mol\; Mg}{24.305\; \cancel{g\; Mg}}=8.23\; mol\; Mg
\end{matrix} \notag \] -
You have more moles of magnesium than of titanium tetrachloride, but the ratio is only
\[\dfrac{mol\; Mg}{mol\; TiCl_{4}} = \dfrac{8.23\; mol}{5.272\; mol} = 1.56 \notag \]Because the ratio of the coefficients in the balanced chemical equation is
\[\dfrac{2\; mol\; Mg}{1 mol\; TiCl_{4}} = 2 \notag \]you do not have enough magnesium to react with all the titanium tetrachloride. If this point is not clear from the mole ratio, you should calculate the number of moles of one reactant that is required for complete reaction of the other reactant. For example, you have 8.23 mol of Mg, so you need (8.23 ÷ 2) = 4.12 mol of TiCl4 for complete reaction. Because you have 5.272 mol of TiCl4, titanium tetrachloride is present in excess. Conversely, 5.272 mol of TiCl4 requires 2 × 5.272 = 10.54 mol of Mg, but you have only 8.23 mol. So magnesium is the limiting reactant.
-
Because magnesium is the limiting reactant, the number of moles of magnesium determines the number of moles of titanium that can be formed:
\( moles\; Ti = 8.23\; \cancel{mol\; Mg}\times \dfrac{1\; mol Ti}{2\; \cancel{mol\; Mg}}=4.12\; mol\; Ti \notag \)Thus only 4.12 mol of Ti can be formed.
-
To calculate the mass of titanium metal that you can obtain, multiply the number of moles of titanium by the molar mass of titanium (47.867 g/mol):
\[ moles\; Ti=mass\; Ti\times molar\; mass\; Ti=4.12\; \cancel{mol\; Ti}\times \dfrac{47.867\; g\; Ti}{1\; mol\; Ti}=197\; g\; Ti \notag \]
Here is a simple and reliable way to identify the limiting reactant in any problem of this sort:
- Calculate the number of moles of each reactant present: 5.272 mol of TiCl4 and 8.23 mol of Mg.
-
Divide the actual number of moles of each reactant by its stoichiometric coefficient in the balanced chemical equation:
\[ \begin{matrix}
TiCl_{4}:\dfrac{5.272\; mol\left ( actual \right )}{1\; mol\;\left ( stoich \right )}=5.272 & Mg:\dfrac{8.23\; mol\left ( actual \right )}{2\; mol\;\left ( stoich \right )}=4.12
\end{matrix} \notag \] - The reactant with the smallest mole ratio is limiting. Magnesium, with a calculated stoichiometric mole ratio of 4.12, is the limiting reactant.
| TiCl4(s) | + 2Mg(s) | → 2MgCl2(s) | + Ti(s) | |
| Mass (g) | 1000 | 200 | ||
| Molecular Weight (g/mol) | 189.67 | 24.31 | ||
| Moles | 5.27 | 8.23 | ||
| Stoichiometric Coefficients |
1 | 2 | ||
| Stoichiometric Equivalents |
5.27 | 4.11 |
Because the number of Stoichiometric Equivalents for the Mg is smaller, it is the limiting reagent. We now simply carry out the Table calculation for Ti(s) to find the mass of Ti produced. Similarly we could calculate the mass of MgCl2(s) produced or even the amount of TiCl4(s) that was consumed in the reaction. Remember we divide going down the table and multiply going up.
| TiCl4(s) | + 2Mg(s) | → 2MgCl2(s) | + Ti(s) | |
| Mass (g) | 1000 | 200 | 196.9 | |
| Molecular Weight (g/mol) | 189.67 | 24.31 | 47.87 | |
| Moles | 5.27 | 8.23 | 4.11 | |
| Stoichiometric Coefficients |
1 | 2 | 1 | |
| Stoichiometric Equivalents |
5.27 | 4.11 | 4.11 |
As you learned in Chapter 1 , density is the mass per unit volume of a substance. If we are given the density of a substance, we can use it in stoichiometric calculations involving liquid reactants and/or products, as Example 12 demonstrates.
Example 12
Ethyl acetate (CH3CO2C2H5) is the solvent in many fingernail polish removers and is used to decaffeinate coffee beans and tea leaves. It is prepared by reacting ethanol (C2H5OH) with acetic acid (CH3CO2H); the other product is water. A small amount of sulfuric acid is used to accelerate the reaction, but the sulfuric acid is not consumed and does not appear in the balanced chemical equation. Given 10.0 mL each of acetic acid and ethanol, how many grams of ethyl acetate can be prepared from this reaction? The densities of acetic acid and ethanol are 1.0492 g/mL and 0.7893 g/mL, respectively.

Given: reactants, products, and volumes and densities of reactants
Asked for: mass of product
Strategy:
A Balance the chemical equation for the reaction.
B Use the given densities to convert from volume to mass. Then use each molar mass to convert from mass to moles.
C Using mole ratios, determine which substance is the limiting reactant. After identifying the limiting reactant, use mole ratios based on the number of moles of limiting reactant to determine the number of moles of product.
D Convert from moles of product to mass of product.
Solution:
A We always begin by writing the balanced chemical equation for the reaction:
\[{C_2}{H_5}OH\left( l \right) + C{H_3}C{O_2}H(aq){\text{ }} \to C{H_3}C{O_2}{C_2}{H_5}(aq) + {H_2}O\left( l \right) \notag \]
B We need to calculate the number of moles of ethanol and acetic acid that are present in 10.0 mL of each. Recall from Chapter 1 " that the density of a substance is the mass divided by the volume:
\[ density=\dfrac{mass}{volume} \notag \]
Rearranging this expression gives mass = (density)(volume). We can replace mass by the product of the density and the volume to calculate the number of moles of each substance in 10.0 mL (remember, 1 mL = 1 cm3):
\( \begin{matrix}
moles\; C_{2}H_{5}OH &= &\dfrac{mass\; C_{2}H_{5}OH}{molar\; mass\; C_{2}H_{5}OH} \\
& \\
&=& \dfrac{volume\; C_{2}H_{5}OH \times density\; C_{2}H_{5}OH}{molar\; mass\; C_{2}H_{5}OH} \\
& \\
&=&100.0\; \cancel{mL\; C_{2}H_{5}OH}\times \dfrac{0.789\; \cancel{g\; C_{2}H_{5}OH}}{1\; \cancel{mL\; C_{2}H_{5}OH}}\dfrac{1\; mol\; mL\; C_{2}H_{5}OH}{46.07\; \cancel{g\; C_{2}H_{5}OH}}\\
& \\
&=& 0.171\;mol\; C_{2}H_{5}OH
\end{matrix} \notag \)
and
\[ \begin{matrix}
moles\; CH_{3}CO_{2}H &= &\dfrac{mass\; CH_{3}CO_{2}H}{molar\; mass\; CH_{3}CO_{2}H} \\
& \\
&=& \dfrac{volume\; CH_{3}CO_{2}H \times density\; CH_{3}CO_{2}H}{molar\; mass\; CH_{3}CO_{2}H} \\
& \\
&=&10.0\; \cancel{mL\; CH_{3}CO_{2}H}\times \dfrac{1.0492\; \cancel{g\; CH_{3}CO_{2}H}}{1\; \cancel{mL\; CH_{3}CO_{2}H}}\dfrac{1\; mol\; mL\; CH_{3}CO_{2}H}{60.05\; \cancel{g\; CH_{3}CO_{2}H}}\\
& \\
&=& 0.175\;mol\; CH_{3}CO_{2}H
\end{matrix} \notag \]
C The number of moles of acetic acid exceeds the number of moles of ethanol. Because the reactants both have coefficients of 1 in the balanced chemical equation, the mole ratio is 1:1. We have 0.171 mol of ethanol and 0.175 mol of acetic acid, so ethanol is the limiting reactant and acetic acid is in excess. The coefficient in the balanced chemical equation for the product (ethyl acetate) is also 1, so the mole ratio of ethanol and ethyl acetate is also 1:1. This means that given 0.171 mol of ethanol, the amount of ethyl acetate produced must also be 0.171 mol:
\[ \begin{matrix}
moles\; ethyl\; acetate &= &mol\; ethanol\times \dfrac{1\; mol\; ethyl\; acetate}{1\; mol\; ethanol} \\
& \\
&=& 0.171\; \cancel{mol\; ethanol} \times \dfrac{1\; mol\; ethyl\; acetate}{1\; \cancel{mol\; ethanol}} \\
& \\
&=& 0.171\;mol\; CH_{3}CO_{2}C_{2}H_{5}
\end{matrix} \notag \]
D The final step is to determine the mass of ethyl acetate that can be formed, which we do by multiplying the number of moles by the molar mass:
\[ \begin{matrix}
mass\; of\; ethyl\; acetate &= &mol\; ethyl\; acetate\times molar\; mass\; ethyl\; acetate \\
& \\
&=& 0.171\; \cancel{mol\; CH_{3}CO_{2}C_{2}H_{5}} \times \dfrac{88.1\; g\; CH_{3}CO_{2}C_{2}H_{5}} {1\; \cancel{mol\; CH_{3}CO_{2}C_{2}H_{5}}} \\
& \\
&=& 15.1\; g\; CH_{3}CO_{2}C_{2}H_{5}
\end{matrix} \notag \]
Thus 15.1 g of ethyl acetate can be prepared in this reaction. If necessary, you could use the density of ethyl acetate (0.9003 g/cm3) to determine the volume of ethyl acetate that could be produced:
\[ \begin{matrix}
volume\; of\; ethyl\; acetate &= & 15.1\; g\; CH_{3}CO_{2}C_{2}H_{5}\times \dfrac{1\; mL CH_{3}CO_{2}C_{2}H_{5}}{0.9003\; \cancel{g\; CH_{3}CO_{2}C_{2}H_{5}}} \\
& & \\
&=& 16.8\;mL\; CH_{3}CO_{2}C_{2}H_{5}
\end{matrix} \notag \]
Exercise
Under appropriate conditions, the reaction of elemental phosphorus and elemental sulfur produces the compound P4S10. How much P4S10 can be prepared starting with 10.0 g of P4 and 30.0 g of S8?
Answer: 35.9 g
Percent Yield
You have learned that when reactants are not present in stoichiometric quantities, the limiting reactant determines the maximum amount of product that can be formed from the reactants. The amount of product calculated in this way is the theoretical yield, which is the maximum amount of product that can be formed from the reactants in a chemical reaction, which theoretically is the amount of product that would be obtained if the reaction occurred perfectly and the method of purifying the product were 100% efficient. The amount you would obtain if the reaction occurred perfectly and your method of purifying the product were 100% efficient.
In reality, you almost always obtain less product than is theoretically possible because of mechanical losses (such as spilling), separation procedures that are not 100% efficient, competing reactions that form undesired products, and reactions that simply do not go all the way to completion, thus resulting in a mixture of products and reactants. This last possibility is a common occurrence, which we call a chemical equilibrium. This is not a static equilibrium where two people are standing holding three balls, but a situation where the rate of forward reaction is balanced by the rate of reverse reaction. You could think of this as jugglers tossing the balls back and forth. So the actual yield (the measured mass of products actually obtained from a reaction). The actual yield is nearly always less than the theoretical yield., the measured mass of products obtained from a reaction, is almost always less than the theoretical yield (often much less). The percent yield (the ratio of the actual yield of a reaction to the theoretical yield multiplied by 100 to give a percentage) of a reaction is the ratio of the actual yield to the theoretical yield, multiplied by 100 to give a percentage:
\[ percent\; yield=\dfrac{actual yield\left ( g \right )}{theoretical\; yield\left ( g \right )} \times 100\]
The method used to calculate the percent yield of a reaction is illustrated in Example 13.
Example 13
Procaine is a key component of Novocain, an injectable local anesthetic used in dental work and minor surgery. Procaine can be prepared in the presence of H2SO4 (indicated above the arrow) by the reaction
\[ \begin{matrix}
C_{7}H_{7}NO_{2} &+C_{6}H_{15}NO & \xrightarrow{H_{2}SO_{4}} & C_{13}H_{20}N_{2}O_{2} & +H_{2}O\\
^{p-aminobenzonic\; acid}& ^{2-diethylaminoethanol} & & ^{procaine} &
\end{matrix} \notag \]
If we carried out this reaction using 10.0 g of p-aminobenzoic acid and 10.0 g of 2-diethylaminoethanol, and we isolated 15.7 g of procaine, what was the percent yield?
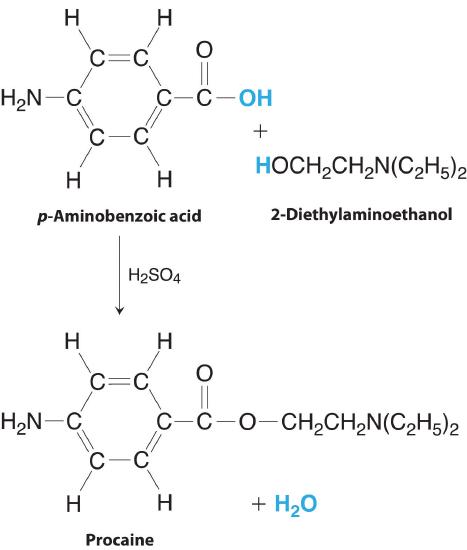
The preparation of procaine. A reaction of p-aminobenzoic acid with 2-diethylaminoethanol yields procaine and water.
Given: masses of reactants and product
Asked for: percent yield
Strategy:
A Write the balanced chemical equation.
B Convert from mass of reactants and product to moles using molar masses and then use mole ratios to determine which is the limiting reactant. Based on the number of moles of the limiting reactant, use mole ratios to determine the theoretical yield.
C Calculate the percent yield by dividing the actual yield by the theoretical yield and multiplying by 100.
Solution:
A From the formulas given for the reactants and the products, we see that the chemical equation is balanced as written. According to the equation, 1 mol of each reactant combines to give 1 mol of product plus 1 mol of water.
B To determine which reactant is limiting, we need to know their molar masses, which are calculated from their structural formulas: p-aminobenzoic acid (C7H7NO2), 137.14 g/mol; 2-diethylaminoethanol (C6H15NO), 117.19 g/mol. Thus the reaction used the following numbers of moles of reactants:
\[ \begin{matrix}
moles\; p-aminobenzoic\; acid & = & 10.0\; \cancel{g}\dfrac{1\; mol}{137.14\; \cancel{g}} & = & 0.0729\; mol\; p-ABA\\
& & & & \\
moles\; 2-diethylaminoethanol & = & 10.0\; \cancel{g}\dfrac{1\; mol}{117.19\; \cancel{g}} & = & 0.0853\; mol\; 2-dAE
\end{matrix} \notag \]
The reaction requires a 1:1 mole ratio of the two reactants, so p-aminobenzoic acid is the limiting reactant. Based on the coefficients in the balanced chemical equation, 1 mol of p-aminobenzoic acid yields 1 mol of procaine. We can therefore obtain only a maximum of 0.0729 mol of procaine. To calculate the corresponding mass of procaine, we use its structural formula (C13H20N2O2) to calculate its molar mass, which is 236.31 g/mol.
\[ theoretical\; yield\; of\; procaine= 0.0729\; \cancel{mol}\times \dfrac{236.31\; g}{1\; \cancel{mol}}=17.2\; g \notag \]
C The actual yield was only 15.7 g of procaine, so the percent yield was
\[ percent\; yield= \dfrac{15.7\; g}{17.2\; g}\times 100=91.3\% \notag \]
(If the product were pure and dry, this yield would indicate that we have very good lab technique!)
Exercise
Lead was one of the earliest metals to be isolated in pure form. It occurs as concentrated deposits of a distinctive ore called galena (PbS), which is easily converted to lead oxide (PbO) in 100% yield by roasting in air via the following reaction:
\[2PbS\left( s \right) + 3{O_2}\left( g \right){\text{ }} \to 2PbO\left( s \right) + 2S{O_2}\left( g \right) \notag \]
The resulting PbO is then converted to the pure metal by reaction with charcoal. Because lead has such a low melting point (327°C), it runs out of the ore-charcoal mixture as a liquid that is easily collected. The reaction for the conversion of lead oxide to pure lead is as follows:
\[PbO\left( s \right) + C\left( s \right){\text{ }} \to Pb\left( l \right) + CO\left( g \right) \notag \]
If 93.3 kg of PbO is heated with excess charcoal and 77.3 kg of pure lead is obtained, what is the percent yield?
Crystalline galena (a) and a sample of lead (b). Pure lead is soft enough to be shaped easily with a hammer, unlike the brittle mineral galena, the main ore of lead.
Answer: 89.2%
Percent yield can range from 0% to 100%.In the laboratory, a student will occasionally obtain a yield that appears to be greater than 100%. This usually happens when the product is impure or is wet with a solvent such as water. If this is not the case, then the student must have made an error in weighing either the reactants or the products. The law of conservation of mass applies even to undergraduate chemistry laboratory experiments! A 100% yield means that everything worked perfectly, and you obtained all the product that could have been produced. Anyone who has tried to do something as simple as fill a salt shaker or add oil to a car’s engine without spilling knows how unlikely a 100% yield is. At the other extreme, a yield of 0% means that no product was obtained. A percent yield of 80%–90% is usually considered good to excellent; a yield of 50% is only fair. In part because of the problems and costs of waste disposal, industrial production facilities face considerable pressures to optimize the yields of products and make them as close to 100% as possible.
Summary
The stoichiometry of a reaction describes the relative amounts of reactants and products in a balanced chemical equation. A stoichiometric quantity of a reactant is the amount necessary to react completely with the other reactant(s). If a quantity of a reactant remains unconsumed after complete reaction has occurred, it is in excess. The reactant that is consumed first and limits the amount of product(s) that can be obtained is the limiting reactant. To identify the limiting reactant, calculate the number of moles of each reactant present and compare this ratio to the mole ratio of the reactants in the balanced chemical equation. The maximum amount of product(s) that can be obtained in a reaction from a given amount of reactant(s) is the theoretical yield of the reaction. The actual yield is the amount of product(s) actually obtained in the reaction; it cannot exceed the theoretical yield. The percent yield of a reaction is the ratio of the actual yield to the theoretical yield, expressed as a percentage.
Key Takeaway
- The stoichiometry of a balanced chemical equation identifies the maximum amount of product that can be obtained.
Conceptual Problems
-
Engineers use conservation of mass, called a “mass balance,” to determine the amount of product that can be obtained from a chemical reaction. Mass balance assumes that the total mass of reactants is equal to the total mass of products. Is this a chemically valid practice? Explain your answer.
-
Given the equation 2H2(g) + O2(g) → 2H2O(g), is it correct to say that 10 g of hydrogen will react with 10 g of oxygen to produce 20 g of water vapor?
-
What does it mean to say that a reaction is stoichiometric?
-
When sulfur is burned in air to produce sulfur dioxide, what is the limiting reactant? Explain your answer.
-
Is it possible for the percent yield to be greater than the theoretical yield? Justify your answer.
Numerical Problems
Please be sure you are familiar with the topics discussed in Essential Skills 2 (Section 7.7 "Essential Skills 2") before proceeding to the Numerical Problems.
-
What is the formula mass of each species?
- ammonium chloride
- sodium cyanide
- magnesium hydroxide
- calcium phosphate
- lithium carbonate
- hydrogen sulfite ion
-
What is the molecular or formula mass of each compound?
- potassium permanganate
- sodium sulfate
- hydrogen cyanide
- potassium thiocyanate
- ammonium oxalate
- lithium acetate
-
How many moles are in each of the following?
- 10.76 g of Si
- 8.6 g of Pb
- 2.49 g of Mg
- 0.94 g of La
- 2.68 g of chlorine gas
- 0.089 g of As
-
How many moles are in each of the following?
- 8.6 g of CO2
- 2.7 g of CaO
- 0.89 g of KCl
- 4.3 g of SrBr2
- 2.5 g of NaOH
- 1.87 g of Ca(OH)2
-
Convert the following to moles and millimoles.
- 1.68 g of Ba(OH)2
- 0.792 g of H3PO4
- 3.21 g of K2S
- 0.8692 g of Cu(NO3)2
- 10.648 g of Ba3(PO4)2
- 5.79 g of (NH4)2SO4
- 1.32 g of Pb(C2H3O2)2
- 4.29 g of CaCl2·6H2O
-
Convert the following to moles and millimoles.
- 0.089 g of silver nitrate
- 1.62 g of aluminum chloride
- 2.37 g of calcium carbonate
- 1.004 g of iron(II) sulfide
- 2.12 g of dinitrogen pentoxide
- 2.68 g of lead(II) nitrate
- 3.02 g of ammonium phosphate
- 5.852 g of sulfuric acid
- 4.735 g of potassium dichromate
-
What is the mass of each substance in grams and milligrams?
- 5.68 mol of Ag
- 2.49 mol of Sn
- 0.0873 mol of Os
- 1.74 mol of Si
- 0.379 mol of H2
- 1.009 mol of Zr
-
What is the mass of each substance in grams and milligrams?
- 2.080 mol of CH3OH
- 0.288 mol of P4
- 3.89 mol of ZnCl2
- 1.800 mol of Fe(CO)5
- 0.798 mol of S8
- 4.01 mol of NaOH
-
What is the mass of each compound in kilograms?
- 6.38 mol of P4O10
- 2.26 mol of Ba(OH)2
- 4.35 mol of K3PO4
- 2.03 mol of Ni(ClO3)2
- 1.47 mol of NH4NO3
- 0.445 mol of Co(NO3)3
-
How many atoms are contained in each?
- 2.32 mol of Bi
- 0.066 mol of V
- 0.267 mol of Ru
- 4.87 mol of C
- 2.74 g of I2
- 1.96 g of Cs
- 7.78 g of O2
-
Convert each number of atoms to milligrams.
- 5.89 × 1022 Pt atoms
- 2.899 × 1021 Hg atoms
- 4.826 × 1022 atoms of chlorine
-
Write a balanced chemical equation for each reaction and then determine which reactant is in excess.
- 2.46 g barium(s) plus 3.89 g bromine(l) in water to give barium bromide
- 1.44 g bromine(l) plus 2.42 g potassium iodide(s) in water to give potassium bromide and iodine
- 1.852 g of Zn metal plus 3.62 g of sulfuric acid in water to give zinc sulfate and hydrogen gas
- 0.147 g of iron metal reacts with 0.924 g of silver acetate in water to give iron(II) acetate and silver metal
- 3.142 g of ammonium phosphate reacts with 1.648 g of barium hydroxide in water to give ammonium hydroxide and barium phosphate
-
Under the proper conditions, ammonia and oxygen will react to form dinitrogen monoxide (nitrous oxide, also called laughing gas) and water. Write a balanced chemical equation for this reaction. Determine which reactant is in excess for each combination of reactants.
- 24.6 g of ammonia and 21.4 g of oxygen
- 3.8 mol of ammonia and 84.2 g of oxygen
- 3.6 × 1024 molecules of ammonia and 318 g of oxygen
- 2.1 mol of ammonia and 36.4 g of oxygen
-
When a piece of zinc metal is placed in aqueous hydrochloric acid, zinc chloride is produced, and hydrogen gas is evolved. Write a balanced chemical equation for this reaction. Determine which reactant is in excess for each combination of reactants.
- 12.5 g of HCl and 7.3 g of Zn
- 6.2 mol of HCl and 100 g of Zn
- 2.1 × 1023 molecules of Zn and 26.0 g of HCl
- 3.1 mol of Zn and 97.4 g of HCl
-
Determine the mass of each reactant needed to give the indicated amount of product. Be sure that the chemical equations are balanced.
- NaI(aq) + Cl2(g) → NaCl(aq) + I2(s); 1.0 mol of NaCl
- NaCl(aq) + H2SO4(aq) → HCl(g) + Na2SO4(aq); 0.50 mol of HCl
- NO2(g) + H2O(l) → HNO2(aq) + HNO3(aq); 1.5 mol of HNO3
-
Determine the mass of each reactant needed to give the indicated amount of product. Be sure that the chemical equations are balanced.
- AgNO3(aq) + CaCl2(s) → AgCl(s) + Ca(NO3)2(aq); 1.25 mol of AgCl
- Pb(s) + PbO2(s) + H2SO4(aq) → PbSO4(s) + H2O(l); 3.8 g of PbSO4
- H3PO4(aq) + MgCO3(s) → Mg3(PO4)2(s) + CO2(g) + H2O(l); 6.41 g of Mg3(PO4)2
-
Determine the percent yield of each reaction. Be sure that the chemical equations are balanced. Assume that any reactants for which amounts are not given are in excess. (The symbol Δ indicates that the reactants are heated.)
- For KClO3 (s) → KCl(s) + O2(g) ,2.14 g of KClO3 produces 0.67 g of O2
- Cu(s) + H2SO4(aq) → CuSO4(aq) + SO2(g) + H2O(l); 4.00 g of copper gives 1.2 g of sulfur dioxide
- AgC2H3O2(aq) + Na3PO4(aq) → Ag3PO4(s) + NaC2H3O2(aq); 5.298 g of silver acetate produces 1.583 g of silver phosphate
-
Each step of a four-step reaction has a yield of 95%. What is the percent yield for the overall reaction?
-
A three-step reaction yields of 87% for the first step, 94% for the second, and 55% for the third. What is the percent yield of the overall reaction?
-
Give a general expression relating the theoretical yield (in grams) of product that can be obtained from x grams of B, assuming neither A nor B is limiting.
\[A + 3B \to 2C \notag \]
-
Under certain conditions, the reaction of hydrogen with carbon monoxide can produce methanol.
- Write a balanced chemical equation for this reaction.
- Calculate the percent yield if exactly 200 g of methanol is produced from exactly 300 g of carbon monoxide.
-
Chlorine dioxide is a bleaching agent used in the paper industry. It can be prepared by the following reaction:
\[NaCl{O_2}\left( s \right) + C{l_2}\left( g \right){\text{ }} \to Cl{O_2}(aq) + NaCl(aq) \notag \]
- What mass of chlorine is needed for the complete reaction of 30.5 g of NaClO2?
- Give a general equation for the conversion of x grams of sodium chlorite to chlorine dioxide.
-
The reaction of propane gas (CH3CH2CH3) with chlorine gas (Cl2) produces two monochloride products: CH3CH2CH2Cl and CH3CHClCH3. The first is obtained in a 43% yield and the second in a 57% yield.
- If you use 2.78 g of propane gas, how much chlorine gas would you need for the reaction to go to completion?
- How many grams of each product could theoretically be obtained from the reaction starting with 2.78 g of propane?
- Use the actual percent yield to calculate how many grams of each product would actually be obtained.
-
Protactinium (Pa), a highly toxic metal, is one of the rarest and most expensive elements. The following reaction is one method for preparing protactinium metal under relatively extreme conditions:
\[ 2PaI_{5}\left ( s \right )\overset{\Delta }{\rightarrow}2Pa\left ( s \right )+5I_{2}\left ( s \right ) \notag \]
- Given 15.8 mg of reactant, how many milligrams of protactinium could be synthesized?
- If 3.4 mg of Pa was obtained, what was the percent yield of this reaction?
- If you obtained 3.4 mg of Pa and the percent yield was 78.6%, how many grams of PaI5 were used in the preparation?
-
Aniline (C6H5NH2) can be produced from chlorobenzene (C6H5Cl) via the following reaction:
\[{C_6}{H_5}Cl\left( l \right) + 2N{H_3}\left( g \right){\text{ }} \to {C_6}{H_5}N{H_2}\left( l \right) + N{H_4}Cl\left( s \right) \notag \]
Assume that 20.0 g of chlorobenzene at 92% purity is mixed with 8.30 g of ammonia.
- Which is the limiting reactant?
- Which reactant is present in excess?
- What is the theoretical yield of ammonium chloride in grams?
- If 4.78 g of NH4Cl was recovered, what was the percent yield?
- Derive a general expression for the theoretical yield of ammonium chloride in terms of grams of chlorobenzene reactant, if ammonia is present in excess.
-
A stoichiometric quantity of chlorine gas is added to an aqueous solution of NaBr to produce an aqueous solution of sodium chloride and liquid bromine. Write the chemical equation for this reaction. Then assume an 89% yield and calculate the mass of chlorine given the following:
- 9.36 × 1024 formula units of NaCl
- 8.5 × 104 mol of Br2
- 3.7 × 108 g of NaCl
Answers
-
- 53.941 amu
- 49.0072 amu
- 58.3197 amu
- 310.177 amu
- 73.891 amu
- 81.071 amu
-
- 0.3831 mol Si
- 4.2 × 10−2 mol Pb
- 0.102 mol Mg
- 6.8 × 10−3 mol La
- 3.78 × 10−2 mol Cl2
- 1.2 × 10−3 mol As
-
- 9.80 × 10−3 mol or 9.80 mmole Ba(OH)2
- 8.08 × 10−3 mol or 8.08 mmole H3PO4
- 2.91 × 10−2 mol or 29.1 mmole K2S
- 4.634 × 10−3 mol or 4.634 mmole Cu(NO3)2
- 1.769 × 10−2 mol 17.69 mmole Ba3(PO4)2
- 4.38 × 10−2 mol or 43.8 mmole (NH4)2SO4
- 4.06 × 10−3 mol or 4.06 mmole Pb(C2H3O2)2
- 1.96 × 10−2 mol or 19.6 mmole CaCl2· 6H2O
-
- 613 g or 6.13 × 105 mg Ag
- 296 g or 2.96 × 105 mg Sn
- 16.6 g or 1.66 × 104 mg Os
- 48.9 g or 4.89 × 104 mg Si
- 0.764 g or 764 mg H2
- 92.05 g or 9.205 × 104 mg Zr
-
- 1.81 kg P4O10
- 0.387 kg Ba(OH)2
- 0.923 kg K3PO4
- 0.458 kg Ni(ClO3)2
- 0.118 kg (NH4)NO3
- 0.109 kg Co(NO3)3
-
- 1.91 × 104 mg Pt
- 965.6 mg Hg
- 2841 mg Cl
-
The balanced chemical equation for this reaction is
2NH3 + 2O2 → N2O + 3H2O- NH3
- NH3
- O2
- NH3
-
- 150 g NaI and 35 g Cl2
- 29 g NaCl and 25 g H2SO4
- 140 g NO2 and 27 g H2O
-
- 80%
- 30%
- 35.7%
-
45%.
-
- CO + 2H2 → CH3OH
- 58.28%
-
- 2.24 g Cl2
- 4.95 g
- 2.13 g CH3CH2CH2Cl plus 2.82 g CH3CHClCH3
-
- chlorobenzene
- ammonia
- 8.74 g ammonium chloride.
- 55%



