Chapter 7.3: Chemical Equations
- Page ID
- 18856
Learning Objectives
- To describe a chemical reaction.
- To calculate the quantities of compounds produced or consumed in a chemical reaction.
As shown in Figure 7.3.1, applying a small amount of heat to a pile of orange ammonium dichromate powder results in a vigorous reaction known as the ammonium dichromate volcano. Heat, light, and gas are produced as a large pile of fluffy green chromium(III) oxide forms. We can describe this reaction with a chemical equationAn expression that gives the identities and quantities of the substances in a chemical reaction. Chemical formulas are used to indicate the reactants on the left and the products on the right. An arrow points from reactants to products., an expression that gives the identities and quantities of the substances in a chemical reaction. Chemical formulas and other symbols are used to indicate the starting material(s), or reactant(s)The starting material(s) in a chemical reaction., which by convention are written on the left side of the equation, and the final compound(s), or product(s)The final compound(s) produced in a chemical reaction., which are written on the right. An arrow points from the reactant to the products:
Figure 7.3.1 An Ammonium Dichromate Volcano: Change during a Chemical Reaction
The starting material (left) is solid ammonium dichromate. A chemical reaction (right) transforms it to solid chromium(III) oxide, depicted showing a portion of its chained structure, nitrogen gas, and water vapor. (In addition, energy in the form of heat and light is released.) During the reaction, the distribution of atoms changes, but the number of atoms of each element does not change. Because the numbers of each type of atom are the same in the reactants and the products, the chemical equation is balanced.
\( \begin{matrix}
\left ( NH_{4} \right )_{2}Cr_{2}O_{7} &\rightarrow Cr_{2}O_{3}+N^{_{2}}+4H_{2}) \\
reactant & products
\end{matrix} \tag{7.3.1} \)
The arrow is read as “yields” or “reacts to form.” So Equation 7.3.1 tells us that ammonium dichromate (the reactant) yields chromium(III) oxide, nitrogen, and water (the products).
The equation for this reaction is even more informative when written as
Equation 7.3.2 is identical to Equation 7.3.1 except for the addition of abbreviations in parentheses to indicate the physical state of each species. The abbreviations are (s) for solid, (l) for liquid, (g) for gas, and (aq) for an aqueous solution, a solution of the substance in water.
Consistent with the law of conservation of mass, the numbers of each type of atom are the same on both sides of Equation 7.3.1 and Equation 7.3.2. (For more information on the law of conservation of mass, see Section 1.4) As illustrated in Figure 7.3.1 , each side has two chromium atoms, seven oxygen atoms, two nitrogen atoms, and eight hydrogen atoms. In a balanced chemical equation, both the numbers of each type of atom and the total charge are the same on both sides. Equation 7.3.1 and Equation 7.3.2 are balanced chemical equations. What is different on each side of the equation is how the atoms are arranged to make molecules or ions. A chemical reaction represents a change in the distribution of atoms but not in the number of atoms. In this reaction, and in most chemical reactions, bonds are broken in the reactants (here, Cr–O and N–H bonds), and new bonds are formed to create the products (here, O–H and N≡N bonds). If the numbers of each type of atom are different on the two sides of a chemical equation, then the equation is unbalanced, and it cannot correctly describe what happens during the reaction. To proceed, the equation must first be balanced.
Note the Pattern
A chemical reaction changes only the distribution of atoms, not the number of atoms.
Interpreting Chemical Equations
In addition to providing qualitative information about the identities and physical states of the reactants and products, a balanced chemical equation provides quantitative information. Specifically, it tells the relative amounts of reactants and products consumed or produced in a reaction. The number of atoms, molecules, or formula units of a reactant or a product in a balanced chemical equation is the coefficientA number greater than 1 preceding a formula in a balanced chemical equation and indicating the number of atoms, molecules, or formula units of a reactant or a product. of that species (e.g., the 4 preceding H2O in Equation 7.3.2). When no coefficient is written in front of a species, the coefficient is assumed to be 1. As illustrated in Figure 7.3.2, the coefficients allow us to interpret Equation 7.3.1 in any of the following ways:
- Two NH4+ ions and one Cr2O72− ion yield 1 formula unit of Cr2O3, 1 N2 molecule, and 4 H2O molecules.
- One mole of (NH4)2Cr2O7 yields 1 mol of Cr2O3, 1 mol of N2, and 4 mol of H2O.
- A mass of 252 g of (NH4)2Cr2O7 yields 152 g of Cr2O3, 28 g of N2, and 72 g of H2O.
- A total of 6.022 × 1023 formula units of (NH4)2Cr2O7 yields 6.022 × 1023 formula units of Cr2O3, 6.022 × 1023 molecules of N2, and 24.09 × 1023 molecules of H2O.
Figure 7.3.2 The Relationships among Moles, Masses, and Formula Units of Compounds in the Balanced Chemical Reaction for the Ammonium Dichromate Volcano
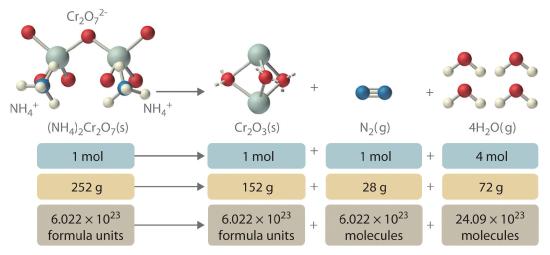
These are all chemically equivalent ways of stating the information given in the balanced chemical equation, using the concepts of the mole, molar or formula mass, and Avogadro’s number. The ratio of the number of moles of one substance to the number of moles of another is called the mole ratioThe ratio of the number of moles of one substance to the number of moles of another, as depicted by a balanced chemical equation.. For example, the mole ratio of H2O to N2 in Equation 7.3.1 is 4:1. The total mass of reactants equals the total mass of products, as predicted by Dalton’s law of conservation of mass: 252 g of (NH4)2Cr2O7 yields 152 + 28 + 72 = 252 g of products. The chemical equation does not, however, show the rate of the reaction (rapidly, slowly, or not at all) or whether energy in the form of heat or light is given off. We will consider these issues in more detail in the second semester.
An important chemical reaction was analyzed by Antoine Lavoisier, an 18th-century French chemist, who was interested in the chemistry of living organisms as well as simple chemical systems. In a classic series of experiments, he measured the carbon dioxide and heat produced by a guinea pig during respiration, in which organic compounds are used as fuel to produce energy, carbon dioxide, and water. Lavoisier found that the ratio of heat produced to carbon dioxide exhaled was similar to the ratio observed for the reaction of charcoal with oxygen in the air to produce carbon dioxide—a process chemists call combustion. Based on these experiments, he proposed that “Respiration is a combustion, slow it is true, but otherwise perfectly similar to that of charcoal.” Lavoisier was correct, although the organic compounds consumed in respiration are substantially different from those found in charcoal. One of the most important fuels in the human body is glucose (C6H12O6), which is virtually the only fuel used in the brain. Thus combustion and respiration are examples of chemical reactions.
Example 9
The balanced chemical equation for the combustion of glucose in the laboratory (or in the brain) is as follows:
\[{C_6}{H_{12}}{O_6}\left( s \right) + 6{O_2}\left( g \right){\text{ }} \to {\text{ }}6C{O_2}\left( g \right) + 6{H_2}O\left( l \right) \notag \]
Construct a table showing how to interpret the information in this equation in terms of
- a single molecule of glucose.
- moles of reactants and products.
- grams of reactants and products represented by 1 mol of glucose.
- numbers of molecules of reactants and products represented by 1 mol of glucose.
Given: balanced chemical equation
Asked for: molecule, mole, and mass relationships
Strategy:
A Use the coefficients from the balanced chemical equation to determine both the molecular and mole ratios.
B Use the molar masses of the reactants and products to convert from moles to grams.
C Use Avogadro’s number to convert from moles to the number of molecules.
Solution:
This equation is balanced as written: each side has 6 carbon atoms, 18 oxygen atoms, and 12 hydrogen atoms. We can therefore use the coefficients directly to obtain the desired information.
A One molecule of glucose reacts with 6 molecules of O2 to yield 6 molecules of CO2 and 6 molecules of H2O.
B One mole of glucose reacts with 6 mol of O2 to yield 6 mol of CO2 and 6 mol of H2O.
C To interpret the equation in terms of masses of reactants and products, we need their molar masses and the mole ratios from part b. The molar masses in grams per mole are as follows: glucose, 180.16; O2, 31.9988; CO2, 44.010; and H2O, 18.015.
\( \begin{matrix}
mass\; of\; reactants &=& mass\; of\; products \\
& \\
g\; glucose &=& g\; CO_{2}+ g\; H_{2}O \\
& \\
1 \cancel{mol\; glucose}\left ( \dfrac{180.16\; g}{1\; \cancel{mol\; glucose}} \right )+6 \cancel{mol\; O_{2}}\left ( \dfrac{31.9988\; g}{1\; \cancel{mol\; O_{2}}} \right ) &=& 6 \cancel{mol\; CO_{2}}\left ( \dfrac{44.010\; g}{1\; \cancel{mol\; CO_{2}}} \right )+6 \cancel{mol\; H_{2}O}\left ( \dfrac{18.0158\; g}{1\; \cancel{mol\; H_{2}O}} \right )\\
& \\
372.15\; g &=& 372.15\; g
\end{matrix} \notag \)
-
C One mole of glucose contains Avogadro’s number (6.022 × 1023) of glucose molecules. Thus 6.022 × 1023 glucose molecules react with (6 × 6.022 × 1023) = 3.613 × 1024 oxygen molecules to yield (6 × 6.022 × 1023) = 3.613 × 1024 molecules each of CO2 and H2O.
In tabular form:
C6H12O6(s) + 6O2(g) → 6CO2(g) + 6H2O(l) a. 1 molecule 6 molecules 6 molecules 6 molecules b. 1 mol 6 mol 6 mol 6 mol c. 180.16 g 191.9928 g 264.06 g 108.09 g d. 6.022 × 1023 molecules 3.613 × 1024 molecules 3.613 × 1024 molecules 3.613 × 1024 molecules
Exercise
Ammonium nitrate is a common fertilizer, but under the wrong conditions it can be hazardous. In 1947, a ship loaded with ammonium nitrate caught fire during unloading and exploded, destroying the town of Texas City, Texas. The explosion resulted from the following reaction:
\[2N{H_4}N{O_3}\left( s \right){\text{ }} \to {\text{ }}2{N_2}\left( g \right) + 4{H_2}O\left( g \right) + {O_2}\left( g \right) \notag \]
Construct a table showing how to interpret the information in the equation in terms of
- individual molecules and ions.
- moles of reactants and products.
- grams of reactants and products given 2 mol of ammonium nitrate.
- numbers of molecules or formula units of reactants and products given 2 mol of ammonium nitrate.
Answer:
| 2NH4NO3(s) | → | 2N2(g) | + | 4H2O(g) | + | O2(g) | |
|---|---|---|---|---|---|---|---|
| a. | 2NH4+ ions and 2NO3− ions | 2 molecules | 4 molecules | 1 molecule | |||
| b. | 2 mol | 2 mol | 4 mol | 1 mol | |||
| c. | 160.0864 g | 56.0268 g | 72.0608 g | 31.9988 g | |||
| d. | 1.204 × 1024 formula units | 1.204 × 1024 molecules | 2.409 × 1024 molecules | 6.022 × 1023 molecules |

Ammonium nitrate can be hazardous. This aerial photograph of Texas City, Texas, shows the devastation caused by the explosion of a shipload of ammonium nitrate on April 16, 1947.
Balancing Simple Chemical Equations
When a chemist encounters a new reaction, it does not usually come with a label that shows the balanced chemical equation. Instead, the chemist must identify the reactants and products and then write them in the form of a chemical equation that may or may not be balanced as first written. Consider, for example, the combustion of n-heptane (C7H16), an important component of gasoline:
The complete combustion of any hydrocarbon with sufficient oxygen always yields carbon dioxide and water (Figure 7.3.3).
Figure 7.3.3 An Example of a Combustion Reaction
The wax in a candle is a high-molecular-mass hydrocarbon, which produces gaseous carbon dioxide and water vapor in a combustion reaction. When the candle is allowed to burn inside a flask, drops of water, one of the products of combustion, form which we can verify using cobalt chloride test paper. We can demonstrate that carbon dioxide is a product by precipitating calcium carbonate from limewater..
Equation 7.3.3 is not balanced: the numbers of each type of atom on the reactant side of the equation (7 carbon atoms, 16 hydrogen atoms, and 2 oxygen atoms) is not the same as the numbers of each type of atom on the product side (1 carbon atom, 2 hydrogen atoms, and 3 oxygen atoms). Consequently, we must adjust the coefficients of the reactants and products to give the same numbers of atoms of each type on both sides of the equation. Because the identities of the reactants and products are fixed, we cannot balance the equation by changing the subscripts of the reactants or the products. To do so would change the chemical identity of the species being described, as illustrated in Figure 7.3.4.
Figure 7.3.4 Balancing Equations
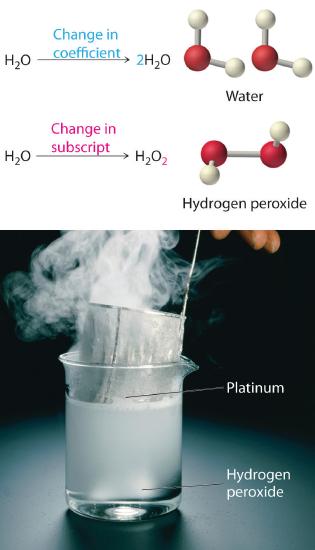
You cannot change subscripts in a chemical formula to balance a chemical equation; you can change only the coefficients. Changing subscripts changes the ratios of atoms in the molecule and the resulting chemical properties. For example, water (H2O) and hydrogen peroxide (H2O2) are chemically distinct substances. H2O2 decomposes to H2O and O2 gas when it comes in contact with the metal platinum, whereas no such reaction occurs between water and platinum.
The simplest and most generally useful method for balancing chemical equations is “inspection,” better known as trial and error. We present an efficient approach to balancing a chemical equation using this method.
Steps in Balancing a Chemical Equation
- Identify the most complex substance.
- Beginning with that substance, choose an element that appears in only one reactant and one product, if possible. Adjust the coefficients to obtain the same number of atoms of this element on both sides.
- Balance polyatomic ions (if present) as a unit.
- Balance the remaining atoms, usually ending with the least complex substance and using fractional coefficients if necessary. If a fractional coefficient has been used, multiply both sides of the equation by the denominator to obtain whole numbers for the coefficients.
- Count the numbers of atoms of each kind on both sides of the equation to be sure that the chemical equation is balanced.
To demonstrate this approach, let’s use the combustion of n-heptane (Equation 7.3.3) as an example.
- Identify the most complex substance. The most complex substance is the one with the largest number of different atoms, which is C7H16. We will assume initially that the final balanced chemical equation contains 1 molecule or formula unit of this substance.
-
Adjust the coefficients. Try to adjust the coefficients of the molecules on the other side of the equation to obtain the same numbers of atoms on both sides. Because one molecule of n-heptane contains 7 carbon atoms, we need 7 CO2 molecules, each of which contains 1 carbon atom, on the right side:
\[{C_7}{H_{16}} + {O_2} \to 7C{O_2} + {H_2}O \tag{7.3.4}\] -
Balance polyatomic ions as a unit. There are no polyatomic ions to be considered in this reaction.
-
Balance the remaining atoms. Because one molecule of n-heptane contains 16 hydrogen atoms, we need 8 H2O molecules, each of which contains 2 hydrogen atoms, on the right side:
\[{C_7}{H_{16}} + {O_2} \to {\text{ }}7C{O_2} + 8{H_2}O \tag{7.3.5}\] -
The carbon and hydrogen atoms are now balanced, but we have 22 oxygen atoms on the right side and only 2 oxygen atoms on the left. We can balance the oxygen atoms by adjusting the coefficient in front of the least complex substance, O2, on the reactant side:
\[{C_7}{H_{16}} + 11{O_2} \to {\text{ }}7C{O_2} + 8{H_2}O \tag{7.3.6}\] - Check your work. The equation is now balanced, and there are no fractional coefficients: there are 7 carbon atoms, 16 hydrogen atoms, and 22 oxygen atoms on each side. Always check to be sure that a chemical equation is balanced.
The assumption that the final balanced chemical equation contains only one molecule or formula unit of the most complex substance is not always valid, but it is a good place to start. Consider, for example, a similar reaction, the combustion of isooctane (C8H18). Because the combustion of any hydrocarbon with oxygen produces carbon dioxide and water, the unbalanced chemical equation is as follows:
- Identify the most complex substance. Begin the balancing process by assuming that the final balanced chemical equation contains a single molecule of isooctane.
-
Adjust the coefficients. The first element that appears only once in the reactants is carbon: 8 carbon atoms in isooctane means that there must be 8 CO2 molecules in the products:
\[{C_8}{H_{18}}\left( l \right) + {O_2}\left( g \right){\text{ }} \to {\text{ 8}}C{O_2}\left( g \right) + {H_2}O\left( g \right) \tag{7.3.8}\] - Balance polyatomic ions as a unit. This step does not apply to this equation.
-
Balance the remaining atoms. Eighteen hydrogen atoms in isooctane means that there must be 9 H2O molecules in the products:
\[{C_8}{H_{18}}\left( l \right) + {O_2}\left( g \right){\text{ }} \to {\text{ 8}}C{O_2}\left( g \right) + 9{H_2}O\left( g \right) \tag{7.3.9}\]The carbon and hydrogen atoms are now balanced, but we have 25 oxygen atoms on the right side and only 2 oxygen atoms on the left. We can balance the least complex substance, O2, but because there are 2 oxygen atoms per O2 molecule, we must use a fractional coefficient (25/2) to balance the oxygen atoms:
\[{C_8}{H_{18}}\left( l \right) + 25/2{O_2}\left( g \right){\text{ }} \to {\text{ 8}}C{O_2}\left( g \right) + 9{H_2}O\left( g \right) \tag{7.3.10}\]Equation 7.3.10 is now balanced, but we usually write equations with whole-number coefficients. We can eliminate the fractional coefficient by multiplying all coefficients on both sides of the chemical equation by 2:
\[2{C_8}{H_{18}}\left( l \right) + 25{O_2}\left( g \right){\text{ }} \to {\text{ 16}}C{O_2}\left( g \right) + 18{H_2}O\left( g \right) \tag{7.3.11}\] - Check your work. The balanced chemical equation has 16 carbon atoms, 36 hydrogen atoms, and 50 oxygen atoms on each side.
Balancing equations requires some practice on your part as well as some common sense. If you find yourself using very large coefficients or if you have spent several minutes without success, go back and make sure that you have written the formulas of the reactants and products correctly.
Example 10
The reaction of the mineral hydroxyapatite [Ca5(PO4)3(OH)] with phosphoric acid and water gives Ca(H2PO4)2·H2O (calcium dihydrogen phosphate monohydrate). Write and balance the equation for this reaction.
Given: reactants and product
Asked for: balanced chemical equation
Strategy:
A Identify the product and the reactants and then write the unbalanced chemical equation.
B Follow the steps for balancing a chemical equation.
Solution:
We must first identify the product and reactants and write an equation for the reaction. The formulas for hydroxyapatite and calcium dihydrogen phosphate monohydrate are given in the problem. Recall that phosphoric acid is H3PO4. The initial (unbalanced) equation is as follows:
\[C{a_5}{(P{O_4})_3}\left( {OH} \right)\left( s \right) + {H_3}P{O_4}\left( {aq} \right) + {H_2}O\left( l \right){\text{ }} \to {\text{ }}Ca{({H_2}P{O_4})_2}\cdot{H_2}O\left( s \right) \notag \]
- Identify the most complex substance. We start by assuming that only one molecule or formula unit of the most complex substance, Ca5(PO4)3(OH), appears in the balanced chemical equation.
-
Adjust the coefficients. Because calcium is present in only one reactant and one product, we begin with it. One formula unit of Ca5(PO4)3(OH) contains 5 calcium atoms, so we need 5 Ca(H2PO4)2·H2O on the right side:
\[C{a_5}{(P{O_4})_3}\left( {OH} \right) + {H_3}P{O_4} + {H_2}O{\text{ }} \to {\text{ }}5Ca{({H_2}P{O_4})_2}\cdot{H_2}O \notag \] -
Balance polyatomic ions as a unit. It is usually easier to balance an equation if we recognize that certain combinations of atoms occur on both sides. In this equation, the polyatomic phosphate ion (PO43−), shows up in three places.In H3PO4, the phosphate ion is combined with three H+ ions to make phosphoric acid (H3PO4), whereas in Ca(H2PO4)2·H2O it is combined with two H+ ions to give the dihydrogen phosphate ion. Thus it is easier to balance PO4 as a unit rather than counting individual phosphorus and oxygen atoms. There are 10 PO4 units on the right side but only 4 on the left. The simplest way to balance the PO4 units is to place a coefficient of 7 in front of H3PO4:
\[C{a_5}{(P{O_4})_3}\left( {OH} \right) + 7{H_3}P{O_4} + {H_2}O{\text{ }} \to {\text{ }}5Ca{({H_2}P{O_4})_2}\cdot{H_2}O \notag \]Although OH− is also a polyatomic ion, it does not appear on both sides of the equation. So oxygen and hydrogen must be balanced separately.
-
Balance the remaining atoms. We now have 30 hydrogen atoms on the right side but only 24 on the left. We can balance the hydrogen atoms using the least complex substance, H2O, by placing a coefficient of 4 in front of H2O on the left side, giving a total of 4 H2O molecules:
\[C{a_5}{(P{O_4})_3}\left( {OH} \right)\left( s \right) + 7{H_3}P{O_4}\left( {aq} \right) + 4{H_2}O\left( l \right){\text{ }} \to {\text{ }}5Ca{({H_2}P{O_4})_2}\cdot{H_2}O\left( s \right) \notag \]The equation is now balanced. Even though we have not explicitly balanced the oxygen atoms, there are 45 oxygen atoms on each side.
- Check your work. Both sides of the equation contain 5 calcium atoms, 7 phosphorus atoms, 30 hydrogen atoms, and 45 oxygen atoms.
Exercise
Fermentation is a biochemical process that enables yeast cells to live in the absence of oxygen. Humans have exploited it for centuries to produce wine and beer and make bread rise. In fermentation, sugars such as glucose are converted to ethanol and carbon dioxide. Write a balanced chemical reaction for the fermentation of glucose.

Commercial use of fermentation. (a) Microbrewery vats are used to prepare beer. (b) The fermentation of glucose by yeast cells is the reaction that makes beer production possible.
Answer: \( {C_6}{H_{12}}{O_6}\left( s \right){\text{ }} \to {\text{ }}2{C_2}{H_5}OH\left( l \right) + 2C{O_2}\left( g \right) \notag \)
Summary
In a chemical reaction, one or more substances are transformed to new substances. A chemical reaction is described by a chemical equation, an expression that gives the identities and quantities of the substances involved in a reaction. A chemical equation shows the starting compound(s)—the reactants—on the left and the final compound(s)—the products—on the right, separated by an arrow. In a balanced chemical equation, the numbers of atoms of each element and the total charge are the same on both sides of the equation. The number of atoms, molecules, or formula units of a reactant or product in a balanced chemical equation is the coefficient of that species. The mole ratio of two substances in a chemical reaction is the ratio of their coefficients in the balanced chemical equation.
Key Takeaway
- A chemical reaction is described by a chemical equation that gives the identities and quantities of the reactants and the products.
Conceptual Problems
-
How does a balanced chemical equation agree with the law of definite proportions?
-
What is the difference between S8 and 8S? Use this example to explain why subscripts in a formula must not be changed.
-
What factors determine whether a chemical equation is balanced?
-
What information can be obtained from a balanced chemical equation? Does a balanced chemical equation give information about the rate of a reaction?
Numerical Problems
-
Balance each chemical equation.
- KI(aq) + Br2(l) → KBr(aq) + I2(s)
- MnO2(s) + HCl(aq) → MnCl2(aq) + Cl2(g) + H2O(l)
- Na2O(s) + H2O(l) → NaOH(aq)
- Cu(s) + AgNO3(aq) → Cu(NO3)2(aq) + Ag(s)
- SO2(g) + H2O(l) → H2SO3(aq)
- S2Cl2(l) + NH3(l) → S4N4(s) + S8(s) + NH4Cl(s)
-
Balance each chemical equation.
- Be(s) + O2(g) → BeO(s)
- N2O3(g) + H2O(l) → HNO2(aq)
- Na(s) + H2O(l) → NaOH(aq) + H2(g)
- CaO(s) + HCl(aq) → CaCl2(aq) + H2O(l)
- CH3NH2(g) + O2(g) → H2O(g) + CO2(g) + N2(g)
- Fe(s) + H2SO4(aq) → FeSO4(aq) + H2(g)
-
Balance each chemical equation.
- N2O5(g) → NO2(g) + O2(g)
- NaNO3(s) → NaNO2(s) + O2(g)
- Al(s) + NH4NO3(s) → N2(g) + H2O(l) + Al2O3(s)
- C3H5N3O9(l) → CO2(g) + N2(g) + H2O(g) + O2(g)
- reaction of butane with excess oxygen
- IO2F(s) + BrF3(l) → IF5(l) + Br2(l) + O2(g)
-
Balance each chemical equation.
- H2S(g) + O2(g) → H2O(l) + S8(s)
- KCl(aq) + HNO3(aq) + O2(g) → KNO3(aq) + Cl2(g) + H2O(l)
- NH3(g) + O2(g) → NO(g) + H2O(g)
- CH4(g) + O2(g) → CO(g) + H2(g)
- NaF(aq) + Th(NO3)4(aq) → NaNO3(aq) + ThF4(s)
- Ca5(PO4)3F(s) + H2SO4(aq) + H2O(l) → H3PO4(aq) + CaSO4·2H2O(s) + HF(aq)
-
Balance each chemical equation.
- NaCl(aq) + H2SO4(aq) → Na2SO4(aq) + HCl(g)
- K(s) + H2O(l) → KOH(aq) + H2(g)
- reaction of octane with excess oxygen
- S8(s) + Cl2(g) → S2Cl2(l)
- CH3OH(l) + I2(s) + P4(s) → CH3I(l) + H3PO4(aq) + H2O(l)
- (CH3)3Al(s) + H2O(l) → CH4(g) + Al(OH)3(s)
-
Write a balanced chemical equation for each reaction.
- Aluminum reacts with bromine.
- Sodium reacts with chlorine.
- Aluminum hydroxide and acetic acid react to produce aluminum acetate and water.
- Ammonia and oxygen react to produce nitrogen monoxide and water.
- Nitrogen and hydrogen react at elevated temperature and pressure to produce ammonia.
- An aqueous solution of barium chloride reacts with a solution of sodium sulfate.
-
Write a balanced chemical equation for each reaction.
- Magnesium burns in oxygen.
- Carbon dioxide and sodium oxide react to produce sodium carbonate.
- Aluminum reacts with hydrochloric acid.
- An aqueous solution of silver nitrate reacts with a solution of potassium chloride.
- Methane burns in oxygen.
- Sodium nitrate and sulfuric acid react to produce sodium sulfate and nitric acid.
Contributors
- Anonymous
Modified by Joshua Halpern



