4.8: Molecular Weight: Mass Contribution Pattern
- Page ID
- 216939
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Use information in a given phrase or word problem to calculate the elemental mass contributions for a compound.
Molecular weight, which is often abbreviated MW, is unique among the molar standards, in that its corresponding equality pattern cannot be immediately developed from readily-available information. Instead, a pattern must be utilized to calculate the mass contribution of each element that is found within the compound that is being considered. The compound's molecular weight, which is determined by adding the mass contributions of each of that compound's constituent elements, can then be rewritten as an equality, formatted as a conversion factor, or represented as a "hidden" conversion factor.
Mass Contribution Pattern
As stated above, molecular weight is differentiated from the previously-discussed molar standards, Avogadro's number, "component within," and atomic weight, in that its value must be calculated prior to the development of its corresponding molar equality or conversion factors. As stated in Section 2.1, a compound must contain two or more elements that are combined in a specific ratio. Therefore, because molecular weight is a molar quantity that relates to the mass of a compound, its value must correspond to the sum of the mass contributions of each of that compound's constituent elements. Furthermore, in order to calculate the mass contribution of a particular element, the individual mass of that element must be multiplied by the quantity of that element that is present within the compound. Note that both of these components are directly associated with a previously-discussed molar standard. The subscript found on an elemental symbol within a compound's chemical formula indicates how many atoms of that element are present within the compound. These subscript values were utilized in the development of "component within" equalities, and the mass of an element corresponds to that element's atomic weight. As a result, the "component within" and atomic weight molar standards must both be applied, as shown in the following mass contribution pattern, in order to correctly calculate the mass contribution of a single element that is found within the compound that is being considered.
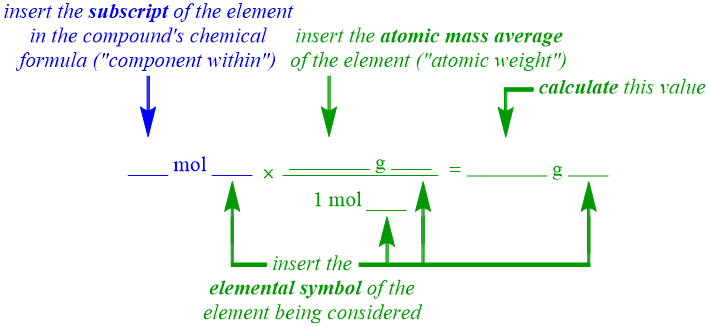
As has been the case for each of the equalities developed in this chapter, all numerical values within a mass contribution calculation must be associated with two units. The primary unit for each component in this mass contribution pattern matches the unit utilized in the corresponding molar standard. The secondary unit for each portion of this pattern should be the chemical formula of the specific element that is being considered in the calculation. As stated in Section 4.3, a chemical name should not be used in this, or any, molar equality or calculation.
Because a molecular weight is a molar standard, its value is calculated for one mole of a compound, by definition. As a result, the left portion of the "component within" equality pattern, which explicitly states a connection to one mole of a compound, is omitted, as its inclusion in the calculation shown above is considered redundant. Therefore, only the right side of the "component within" equality pattern is incorporated into the mass contribution pattern. As stated in Section 4.5, because a "component within" equality establishes the relative quantity of an element that is present within a compound, the subscript for the particular element being considered should occupy the numerical position of the portion of the "component within" equality that is included in the mass contribution pattern, as shown above.
Both components of the atomic weight equality pattern are included, in the form of a conversion factor, in a mass contribution pattern. In particular, the left side of the atomic weight equality pattern, which contains a mole-based unit, must be written in the denominator of this conversion factor, in order to completely cancel the unit found within the "component within" portion of this calculation pattern. While the "component within" portion of this calculation pattern represents the quantity of the element that is present within the compound, an atomic weight always corresponds to one mole of that element. Therefore, while the numerical value of the "component within" portion in a mass contribution calculation can vary, the denominator within the atomic weight conversion always has a numerical value of 1. The remaining portion of the atomic weight equality pattern, which includes the atomic mass average for the element that is being considered, becomes in the numerator in the resultant conversion factor. Recall that an atomic mass average, which is a weighted average of the mass numbers for all of the possible isotopes of an element, is found underneath the elemental symbol for an element on the periodic table. Furthermore, in order to standardize atomic weight calculations, atomic mass averages should be recorded to the hundredths place in an atomic weight equality or conversion factor.
The unit that results upon this cancelation is "g ____," where the "blank" is occupied by the chemical formula of the specific element that is that is being considered in the calculation. Because the pattern shown above is intended to calculate the mass contribution of a single element that is found within the compound that is being considered, "g ____" is an acceptable unit of measurement for this desired quantity. The numerical solution is calculated by multiplying the subscript value found in the "component within" portion of this calculation pattern by the atomic mass average found in the atomic weight conversion factor, and then dividing by the molar quantity in the denominator of the atomic weight conversion factor. Recall that, when using a calculator, the conversion factor should be entered in parentheses, or the "=" key should be used after each division. Finally, in order to standardize mass contribution calculations, each calculated value should be recorded to the hundredths place.
For example, consider the phrase "grams of ZnBr2."
The reference to a mass unit, "grams," in the given phrase, coupled with the knowledge that ZnBr2, zinc bromide, is a compound, indicates that a mass-based molecular weight equality should be developed. The information that is found in a molecular weight equality is determined by utilizing the mass contribution pattern that is shown above to calculate the mass contribution of each element that is found within the corresponding compound. Because ZnBr2, zinc bromide, contains two elements, the pattern that is shown above is applied once for Zn, zinc, and once for Br, bromine. In each mass contribution calculation,
- the chemical formula of the element that is being considered is written as the secondary unit in all portions of this pattern, as chemical names should not be used in this, or any, molar equality or calculation;
- the subscript for the element that is being considered, as found in the compound's chemical formula, is inserted into the "component within" portion of the mass contribution pattern;
- the atomic mass average of the element that is being considered is recorded to the hundredths place in the numerator of the atomic weight conversion factor; and
- the resultant calculated value is reported to the hundredths place.
The mass contribution calculations for ZnBr2, zinc bromide, are shown below.
\( {\text {1}}\) \({\cancel{\rm{mol} \; \rm{Zn}}}\) × \( \dfrac{65.39 \; \rm{g} \; \rm{Zn}}{1\; \cancel{\rm{mol} \; \rm{Zn}}}\) = \( {\text {65.39}}\) \({\rm{g} \; \rm{Zn}}\)
\( {\text {2}}\) \({\cancel{\rm{mol} \; \rm{Br}}}\) × \( \dfrac{79.90 \; \rm{g} \; \rm{Br}}{1\; \cancel{\rm{mol} \; \rm{Br}}}\) = \( {\text {159.80}}\) \({\rm{g} \; \rm{Br}}\)
Calculate all mass contributions that are relevant to the phrase "milligrams of copper (I) sulfite."
Solution
The reference to a mass unit, "milligrams," in the given phrase, coupled with the knowledge that copper (I) sulfite, Cu2SO3, is a compound, indicates that a mass-based molecular weight equality should be developed. The information that is found in a molecular weight equality is determined by calculating the mass contribution of each element that is found within the corresponding compound. The chemical formula for copper (I) sulfite, "Cu2SO3," is derived by applying the Chapter 3 rules for determining ionic chemical formulas. Because copper (I) sulfite, Cu2SO3, contains three elements, the pattern that is shown above is applied once for copper, Cu, once for sulfur, S, and once for oxygen, O. In each mass contribution calculation,
- the chemical formula of the element that is being considered is written as the secondary unit in all portions of this pattern, as chemical names should not be used in this, or any, molar equality or calculation;
- the subscript for the element that is being considered, as found in the compound's chemical formula, is inserted into the "component within" portion of the mass contribution pattern;
- the atomic mass average of the element that is being considered is recorded to the hundredths place in the numerator of the atomic weight conversion factor; and
- the resultant calculated value is reported to the hundredths place.
The mass contribution calculations for copper (I) sulfite, Cu2SO3, are shown below.
\( {\text {2}}\) \({\cancel{\rm{mol} \; \rm{Cu}}}\) × \( \dfrac{63.55 \; \rm{g} \; \rm{Cu}}{1\; \cancel{\rm{mol} \; \rm{Cu}}}\) = \( {\text {127.10}}\) \({\rm{g} \; \rm{Cu}}\)
\( {\text {1}}\) \({\cancel{\rm{mol} \; \rm{S}}}\) × \( \dfrac{32.07 \; \rm{g} \; \rm{S}}{1\; \cancel{\rm{mol} \; \rm{S}}}\) = \( {\text {32.07}}\) \({\rm{g} \; \rm{S}}\)
\( {\text {3}}\) \({\cancel{\rm{mol} \; \rm{O}}}\) × \( \dfrac{16.00 \; \rm{g} \; \rm{O}}{1\; \cancel{\rm{mol} \; \rm{O}}}\) = \( {\text {48.00}}\) \({\rm{g} \; \rm{O}}\)
Calculate all mass contributions that are relevant to the phrase "grams of molecular nitrogen."
- Answer
- The reference to a mass unit, "grams," in the given phrase, coupled with the knowledge that molecular nitrogen, N2, is a compound, indicates that a mass-based molecular weight equality should be developed. The information that is found in a molecular weight equality is determined by calculating the mass contribution of each element that is found within the corresponding compound. The chemical formula for molecular nitrogen, N2, is derived by applying the Chapter 3 rules for determining diatomic covalent chemical formulas. Because molecular nitrogen, N2, contains one element, the pattern that is shown above is applied once for nitrogen, N. In the mass contribution calculation,
- the chemical formula of the element that is being considered is written as the secondary unit in all portions of this pattern, as chemical names should not be used in this, or any, molar equality or calculation;
- the subscript for the element that is being considered, as found in the compound's chemical formula, is inserted into the "component within" portion of the mass contribution pattern;
- the atomic mass average of the element that is being considered is recorded to the hundredths place in the numerator of the atomic weight conversion factor; and
- the resultant calculated value is reported to the hundredths place.
\( {\text {2}}\) \({\cancel{\rm{mol} \; \rm{N}}}\) × \( \dfrac{14.01 \; \rm{g} \; \rm{N}}{1\; \cancel{\rm{mol} \; \rm{N}}}\) = \( {\text {28.02}}\) \({\rm{g} \; \rm{N}}\)

