4.9: Molecular Weight: Calculations, Equality Pattern, and Conversion Factor Representations
- Page ID
- 217209
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Calculate the molecular weight of a compound.
- Represent a molecular weight as a molar equality, a conversion factor, and a "hidden" conversion factor.
As stated in the previous section, molecular weight, which is often abbreviated MW, is unique among the molar standards, in that its equality pattern cannot be immediately developed from readily-available information. Instead, the mass contribution pattern that was discussed in the previous section must be utilized to calculate the mass contribution of each element that is found within the compound that is being considered. The compound's molecular weight, which is determined by adding the mass contributions of each of that compound's constituent elements, can then be rewritten as an equality, formatted as a conversion factor, or represented as a "hidden" conversion factor.
Calculating and Expressing Molecular Weights
As stated above, the numerical value of a molecular weight corresponds to the sum of the mass contributions of all of that compound's constituent elements. As has been the case for all previously-discussed atomic weight and molecular weight calculations, the resultant numerical value should be recorded to the hundredths place. Once calculated, a molecular weight can be rewritten as an equality, formatted as a conversion factor, or represented as a "hidden" conversion factor.
Molecular Weight Equality Pattern
Because a molecular weight is a molar standard, its value is calculated for one mole of a compound, by definition. Therefore, the numerical value of the molecular weight of a compound, which is calculated by adding the mass contributions of all of that compound's constituent elements, can be equated to one mole of that compound. This relationship can be represented in an equality pattern, as shown below.

The secondary unit positions, which are indicated as "blanks" in the equality pattern shown above, should be occupied by units that are relevant to the identity of the specific chemical that is referenced in a given problem. In a molecular weight equality, the chemical formula of the entire compound that is being considered should be inserted into both of these positions. As stated above, the numerical value of the molecular weight of a compound is calculated by adding the mass contributions of all of a compound's constituent elements. Therefore, all of that compound's elements should also be indicated by the unit that is associated with this numerical value. As a result, the chemical formula of the entire compound, which represents the relative ratios of all of the elements that are present within a compound, is inserted into a molecular weight equality. As was the case in an atomic weight equality, the relative order of the two units on the right side of a molecular weight equality should not be interchanged.
Molecular Weight Conversion Factors
All equalities can be re-written as conversion factors. To create a conversion factor from the equality pattern shown above, the quantity on the left side of the equal sign becomes the numerator of a fraction, and the other quantity is written in the denominator. A second conversion factor can be developed by interchanging where each quantity is written, relative to the fraction bar. Both of the resultant conversion factors are shown below.
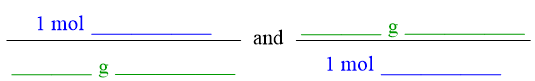
Recall that numerical values of "1" are often unwritten in chemistry. Therefore, the "1"s can be removed from each of these conversion factors, as shown below.
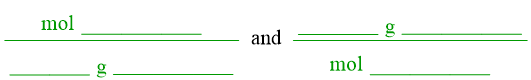
Molecular Weight as a "Hidden" Conversion Factor
The orientation of the conversion factor that is shown on the right is analogous to the formatting utilized in "hidden" conversion factors, which were discussed in Section 1.11. These rates were labeled as "hidden," because the information that they contained were presented in a verbal format, such as "45 miles per hour," within the context of a word problem. Based on the conversion factor that is shown on the right, a molecular weight can be condensed into a "hidden" conversion factor format, as shown below.
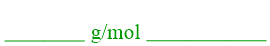
As there is no longer an explicitly-written numerical value in the denominator of the associated conversion factor, the value in the numerator, which corresponds to the calculated molecular weight of the compound that is being considered, is directly inserted as the numerical value in the molecular weight representation shown above. The primary unit that is shown above, "g/mol," results because the units that are found in the numerator and the denominator in the associated conversion factor do not match. Therefore, unit cancelation cannot occur, and the unit for molecular weight, when represented as a "hidden" conversion factor, must contain both "g" and "mol," related to one another in a fractional format. Finally, the remaining unit position should be occupied by the chemical formula of the compound that is being considered. While this chemical formula appears in both the numerator and the denominator in the conversion factor that is shown above and, therefore, should cancel, all numerical values that have been discussed in this chapter must be associated with two units. As a result, this chemical formula must be included as the secondary unit in a "hidden" conversion factor representation of molecular weight.
For example, consider the phrase "grams of ZnBr2."
The reference to a mass unit, "grams," in the given phrase, coupled with the knowledge that ZnBr2, zinc bromide, is a compound, indicates that a mass-based molecular weight equality should be developed. The information that is found in a molecular weight equality is determined by calculating the mass contribution of each element that is found within the corresponding compound. The mass contributions for ZnBr2, zinc bromide, as calculated in Section 4.8, are replicated below.
\( {\text {1}}\) \({\cancel{\rm{mol} \; \rm{Zn}}}\) × \( \dfrac{65.39 \; \rm{g} \; \rm{Zn}}{1\; \cancel{\rm{mol} \; \rm{Zn}}}\) = \( {\text {65.39}}\) \({\rm{g} \; \rm{Zn}}\)
\( {\text {2}}\) \({\cancel{\rm{mol} \; \rm{Br}}}\) × \( \dfrac{79.90 \; \rm{g} \; \rm{Br}}{1\; \cancel{\rm{mol} \; \rm{Br}}}\) = \( {\text {159.80}}\) \({\rm{g} \; \rm{Br}}\)
The numerical value of the molecular weight for ZnBr2, zinc bromide, 225.19, is found by adding these mass contributions. This information can be rewritten as an equality, formatted as a conversion factor, or represented as a "hidden" conversion factor.
In order to develop a molar equality based on the molecular weight of ZnBr2, zinc bromide, the calculated molecular weight is inserted into the equality pattern that is shown above. Because the numerical value of a compound's molecular weight is calculated by adding the mass contributions of all of a compound's constituent elements, all of those elements must be indicated by the unit that is associated with this numerical value. Therefore, the chemical formula of the entire compound is inserted into a molecular weight equality. As was the case in an atomic weight equality, chemical names should not be used, and the relative order of the two units on the right side of a molecular weight equality should not be interchanged.
The molecular weight equality of ZnBr2, zinc bromide, is shown below.
1 mol ZnBr2 = 225.19 g ZnBr2
This equality can be re-written in a conversion factor format. To create a conversion factor from the equality pattern that is shown above, the quantity on the left side of the equal sign becomes the numerator of a fraction, and the other quantity is written in the denominator. A second conversion factor can be developed by interchanging where each quantity is written, relative to the fraction bar. Because numerical values of "1" are often unwritten in chemistry, the "1"s can be removed from each of the resultant conversion factors, as shown below.
\( \dfrac{\text{ mol } \ce{ZnBr_2}}{225.19 {\text{ g }} \ce{ZnBr_2}} \) and \( \dfrac{225.19 {\text{ g }} \ce{ZnBr_2}}{\text{ mol } \ce{ZnBr_2}} \)
Finally, based on the conversion factor that is shown on the right, this molecular weight can be condensed into a "hidden" conversion factor format. Since as there is no longer an explicitly-written numerical value in the denominator of the associated conversion factor, the value in the numerator becomes the numerical value in the "hidden" conversion factor that is shown below. The primary unit, "g/mol," results because the units that are found in the numerator and the denominator in the associated conversion factor do not match. Therefore, unit cancelation cannot occur, and the unit for molecular weight, when represented as a "hidden" conversion factor, must contain both "g" and "mol," related to one another in a fractional format. Finally, the remaining unit position should be occupied by the chemical formula of the compound that is being considered. While this chemical formula appears in both the numerator and the denominator in the conversion factor that is shown above and, therefore, should cancel, all numerical values discussed in this chapter must be associated with two units. As a result, this chemical formula must be included as the secondary unit in a "hidden" conversion factor representation of molecular weight, as shown below.
225.19 g/mol ZnBr2
Calculate the molecular weight of copper (I) sulfite, and represent the resultant solution as a molar equality, a conversion factor, and a hidden conversion factor. The mass contributions for copper (I) sulfite, Cu2SO3, as calculated in Example 4.8.1, are replicated below.
\( {\text {2}}\) \({\cancel{\rm{mol} \; \rm{Cu}}}\) × \( \dfrac{63.55 \; \rm{g} \; \rm{Cu}}{1\; \cancel{\rm{mol} \; \rm{Cu}}}\) = \( {\text {127.10}}\) \({\rm{g} \; \rm{Cu}}\)
\( {\text {1}}\) \({\cancel{\rm{mol} \; \rm{S}}}\) × \( \dfrac{32.07 \; \rm{g} \; \rm{S}}{1\; \cancel{\rm{mol} \; \rm{S}}}\) = \( {\text {32.07}}\) \({\rm{g} \; \rm{S}}\)
\( {\text {3}}\) \({\cancel{\rm{mol} \; \rm{O}}}\) × \( \dfrac{16.00 \; \rm{g} \; \rm{O}}{1\; \cancel{\rm{mol} \; \rm{O}}}\) = \( {\text {48.00}}\) \({\rm{g} \; \rm{O}}\)
Solution
The numerical value of the molecular weight of copper (I) sulfite, Cu2SO3, 207.17, is determined by adding the mass contributions that are shown above.
In order to develop a molar equality based on the molecular weight of copper (I) sulfite, Cu2SO3, the calculated molecular weight is inserted into the equality pattern that is shown above. Because the numerical value of a compound's molecular weight is calculated by adding the mass contributions of all of a compound's constituent elements, all of those elements must be indicated by the unit that is associated with this numerical value. Therefore, the chemical formula of the entire compound is inserted into a molecular weight equality. As was the case in an atomic weight equality, chemical names should not be used, and the relative order of the two units on the right side of a molecular weight equality should not be interchanged.
The molecular weight equality for copper (I) sulfite, Cu2SO3, is shown below.
1 mol Cu2SO3 = 207.17 g Cu2SO3
This equality can be re-written in a conversion factor format. To create a conversion factor from the equality pattern that is shown above, the quantity on the left side of the equal sign becomes the numerator of a fraction, and the other quantity is written in the denominator. A second conversion factor can be developed by interchanging where each quantity is written, relative to the fraction bar. Because numerical values of "1" are often unwritten in chemistry, the "1"s can be removed from each of the resultant conversion factors, as shown below.
\( \dfrac{\text{ mol } \ce{Cu_2SO_3}}{207.17 {\text{ g }} \ce{Cu_2SO_3}} \) and \( \dfrac{207.17 {\text{ g }} \ce{Cu_2SO_3}}{\text{ mol } \ce{Cu_2SO_3}} \)
Finally, based on the conversion factor that is shown on the right, this molecular weight can be condensed into a "hidden" conversion factor format. Since as there is no longer an explicitly-written numerical value in the denominator of the associated conversion factor, the value in the numerator becomes the numerical value in the "hidden" conversion factor that is shown below. The primary unit, "g/mol," results because the units that are found in the numerator and the denominator in the associated conversion factor do not match, and, therefore, cannot cancel. Finally, the remaining unit position is occupied by the chemical formula of the compound that is being considered, in order to have a second unit associated with the molecular weight for this compound, as shown below.
207.17 g/mol Cu2SO3
Calculate the molecular weight of molecular nitrogen, and represent the resultant solution as a molar equality, a conversion factor, and a hidden conversion factor. The mass contribution for molecular nitrogen, N2, as calculated in Exercise 4.8.1, is replicated below.
\( {\text {2}}\) \({\cancel{\rm{mol} \; \rm{N}}}\) × \( \dfrac{14.01 \; \rm{g} \; \rm{N}}{1\; \cancel{\rm{mol} \; \rm{N}}}\) = \( {\text {28.02}}\) \({\rm{g} \; \rm{N}}\)
- Answer
- As only a single mass contribution calculation was necessary for this compound, the resultant numerical solution, 28.02, corresponds to the molecular weight of molecular nitrogen, N2.
In order to develop a molar equality based on the molecular weight of molecular nitrogen, N2, the molecular weight for this compound is inserted into the equality pattern that is shown above, and the chemical formula of the entire compound is utilized as the secondary unit in the resultant equality. As was the case in an atomic weight equality, chemical names should not be used, and the relative order of the two units on the right side of a molecular weight equality should not be interchanged. The molecular weight equality for molecular nitrogen, N2, is shown below.1 mol N2 = 28.02 g N2
This equality can be re-written in a conversion factor format, using the methods that have been described previously. Because numerical values of "1" are often unwritten in chemistry, the "1"s can be removed from each of the resultant conversion factors, as shown below.\( \dfrac{\text{ mol } \ce{N_2}}{28.02 {\text{ g }} \ce{N_2}} \) and \( \dfrac{28.02 {\text{ g }} \ce{N_2}}{\text{ mol } \ce{N_2}} \)
Finally, based on the conversion factor that is shown on the right, this molecular weight can be condensed into a "hidden" conversion factor format. The value in the numerator of this conversion factor becomes the numerical value in the "hidden" conversion factor that is shown below. The primary unit, "g/mol," results because the units that are found in the numerator and the denominator in the associated conversion factor do not match, and, therefore, cannot cancel. Finally, the remaining unit position is occupied by the chemical formula of the compound that is being considered.28.02 g/mol N2

