4.7: Atomic Weight: Equality Pattern and Conversions
- Page ID
- 216938
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Use information in a given phrase or word problem to write atomic weight equalities.
- Apply an atomic weight conversion factor to convert between a molar quantity and an elemental mass.
- Apply multiple conversion factors to convert between an elemental mass and a particle count.
Upon establishing that an atomic weight molar relationship is required to solve a problem, a corresponding atomic weight equality must be developed. Then, using dimensional analysis, the resultant equality can be applied as a conversion factor, in order to bring about a desired unit transformation.
Atomic Weight Equality Pattern
As stated in Section 4.1, an equality pattern contains one number and two units on both sides of an equal sign. On the left side of the atomic weight equality pattern shown below, one of these units, "mol," is defined. The first unit on the right side of this equality pattern is "g." While "grams," "kilograms," and "milligrams" are all indicator words associated with developing an atomic weight equality, "grams" is the most common of these units and, therefore, is used in the atomic weight equality pattern. The secondary unit positions, which are indicated as "blanks" in the equality pattern shown below, should be occupied by units that are relevant to the identity of the specific chemical that is referenced in a given problem. In particular, the elemental symbol of the element that is being considered should be inserted into both of these positions. Therefore, as is the case in an Avogadro's number equality, the chemical formulas written on both sides of an atomic weight equality should match. As stated in Section 4.3, a chemical name should not be used in this, or any, equality. Finally, the relative order of the two units on the right side of an atomic weight equality should not be interchanged.
In accordance with both of the previously-developed patterns, a numerical value of "1" is specified on the left side of an atomic weight equality. Recall that Avogadro's number, 6.02 × 1023, occupies the numerical position on the right side of an Avogadro's number equality. However, as is the case in the "component within" pattern, a "blank" is present in this position in the atomic weight equality pattern that is shown below. As a "component within" equality establishes the relative ratios of the elements that are present within a compound, the subscript for the particular element being considered is inserted into this position in the corresponding equality. However, an atomic weight equality relates to the mass of an element. Therefore, the atomic mass average of the element that is mentioned in the problem should occupy the numerical position on the right side of an atomic weight equality.
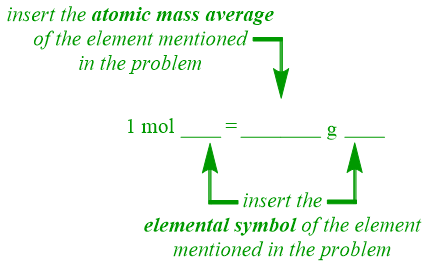
An atomic mass average is a weighted average of the mass numbers for all of the possible isotopes of an element. Recall that the number of neutrons contained in an element can vary from atom to atom, and that changing the number of neutrons present will, in turn, cause these individual atoms to have different calculated mass numbers. These individual atomic "versions" of an element are isotopes, which are defined to have the same atomic numbers (and, therefore, contain the same number of protons) but different mass numbers (and, consequently, possess differing numbers of neutrons). For spatial reasons, listing the mass numbers for all of an element's isotopes within a single box on the periodic table is impractical. Instead, a weighted average, called an atomic mass average, is calculated. A weighted average takes into account not only the mass number of each isotope, but also how prevalent, or common, that isotope is in nature, relative to each of that element's other isotopes. Therefore, an atomic mass average is a quantity that truly represents all isotopes of a given element, making it appropriate for inclusion on the periodic table. The atomic mass average of an element is recorded underneath the elemental symbol for that element on the periodic table. As some elements have been studied more thoroughly than others, atomic mass averages are known to varying degrees of accuracy and, consequently, are not recorded to a consistent decimal place across the periodic table. Therefore, to standardize atomic weight calculations, atomic mass averages should be recorded to the hundredths place in an atomic weight equality.
For example, consider the phrase "grams of Xe."
The reference to a mass unit, "grams," in the given phrase, coupled with the knowledge that Xe, xenon, is an element, indicates that a mass-based atomic weight equality should be developed. Since an elemental symbol was provided in the given phrase, the symbol "Xe" is directly incorporated into the secondary unit positions on both sides of the equality that is being developed. Finally, the atomic mass average of xenon, Xe, the element that is referenced in the given phrase, is 131.29, based on the numerical value that is written underneath its elemental symbol on the periodic table. As this value is already recorded to the hundredths place, it can be directly inserted into the numerical position on the right side of this atomic weight equality, as shown below.
1 mol Xe = 131.29 g Xe
Write an equality appropriate to the phrase "kilograms of lead."
Solution
The reference to a mass unit, "kilograms," in the given phrase, coupled with the knowledge that lead, Pb, is an element, indicates that a mass-based atomic weight equality should be developed. While "kilograms" is the specific indicator word that is present in the given phrase, "grams" is the most common mass unit and, therefore, is used as the first unit on the right side of an atomic weight equality. The chemical name that is referenced in the given statement, "lead," should not be used in this, or any, equality. Instead, the corresponding elemental symbol, "Pb," is incorporated into the remaining unit positions in the equality that is being developed. Finally, the atomic mass average of lead, Pb, is 207.2, based on the numerical value that is written underneath its elemental symbol on the periodic table. However, this value is only recorded to the tenths place, which does not meet the decimal place standard that was defined above. Therefore, when this value is inserted into the numerical position on the right side of an atomic weight equality, it must be recorded with a zero in the hundredths place, as shown below.
1 mol Pb = 207.20 g Pb
Applying Atomic Weight Equalities as Conversion Factors
Once an appropriate atomic weight equality has been developed, the information that it contains can be re-written in the form of a conversion factor, which can then be applied to bring about a desired unit transformation. As stated previously, the quantity containing the unit being canceled must be written in the denominator of a conversion factor. This will cause the given unit, which appears in a numerator, to be divided by itself, since the same unit appears in the denominator of the conversion factor. Since any quantity that is divided by itself "cancels," orienting the conversation factor in this way results in the elimination of the undesirable unit. However, remember that both components of the equalities that are developed in this chapter contain two units. Therefore, in order to achieve complete unit cancelation, a conversion factor that results in the simultaneous elimination of both units must be applied.
For example, use a conversion factor based on the equality developed above for Xe to calculate how many grams of Xe are present in 8.0 moles of Xe.
As stated above, the reference to a mass unit, "grams," in the given problem, coupled with the knowledge that Xe, xenon, is an element, indicates that a mass-based atomic weight equality should be developed and applied to solve this problem. The equality that was generated to correspond with the phrase "grams of Xe" is replicated below.
1 mol Xe = 131.29 g Xe
To create a conversion factor from this equality, the quantity on the left side of the equal sign is written in the numerator of a fraction, and the other quantity is written in the denominator. A second conversion factor can be developed by interchanging where each quantity is written, relative to the fraction bar. Both of the resultant conversion factors are shown below.
\( \dfrac{1 \text{ mol Xe} }{131.29 {\text{ g Xe}}} \) and \( \dfrac{131.29 {\text{ g Xe}}}{1 \text{ mol Xe }} \)
However, only one of these conversion factors will allow for the complete cancelation of the given unit, "moles of Xe," since both of the units that are being canceled must be written in the denominator of the conversion factor that should be applied to solve the given problem. Since the intent of this problem is to eliminate the unit "moles of Xe," the conversion factor on the right must be used. Therefore,
\( {8.0 \; \cancel{\rm{mol} \; \rm{Xe}}} \times\) \( \dfrac{131.29 \; \rm{g} \; \rm{Xe}}{1 \; \cancel{\rm{mol} \; \rm{Xe}}}\)
The solution is calculated by multiplying the given number by the value in each numerator, and then dividing by the quantity in each denominator. Recall that, when using a calculator, each conversion factor should be entered in parentheses, or the "=" key should be used after each division. In this case,
8.0 × (131.29 g Xe ÷ 1) = 1,050.32 g Xe ≈ 1,100 g Xe
Finally, remember that the correct number of significant figures should be applied to any calculated quantity. Since the math involved in dimensional analysis is multiplication and division, the number of significant figures in each number being multiplied or divided must be counted, and the answer must be limited to the lesser count of significant figures. Neither the given number nor the atomic mass average that was utilized above are exact numbers. As the given number contains fewer significant figures, the final answer should be rounded to two significant digits, as shown above.
Use a conversion factor based on the equality developed in Example \(\PageIndex{1}\) to calculate how many moles of lead contain 0.98 kilograms of lead.
Solution
The reference to a mass unit, "kilograms," in the given problem, coupled with the knowledge that lead, Pb, is an element, indicates that a mass-based atomic weight equality should be developed and applied to solve this problem. The equality that was generated to correspond with the phrase "kilograms of lead" is replicated below.
1 mol Pb = 207.20 g Pb
However, this equality cannot be used to completely eliminate the unit "kilograms of lead," as the mass unit that is referenced in the problem, "kilograms," and the mass unit included in the atomic weight equality, "grams," do not match. Therefore, a prefix modifier equality that relates these two units must first be developed and applied. As discussed in Section 1.8, a unit that contains a prefix modifier, such as "kilograms," can be related back to its base unit, "grams," by replacing the prefix modifier, "kilo" (k), with its meaning, "103". The base unit, gram (g), is written with both the prefix modifier and its meaning. Finally, since their base units (grams) match, and the prefix modifier and its meaning are equivalent, these two quantities can be equated to one another, as shown below.
kg = 103 g
While not absolutely necessary, a prefix modifier equality can be simplified by rewriting the numerical value in decimal format, as follows.
kg = 1,000 g
Before applying one of these relationships to cancel the given unit, the chemical formula for lead, Pb, must be added as a secondary unit on each side of the equal sign, as all equalities in this chapter must contain two units. After incorporating this elemental symbol, either equality can be applied to completely cancel the given unit, "kilograms of lead." Regardless of which equality is selected, the quantity on the left side of the equal sign becomes the denominator in the first conversion factor that is applied to solve the given problem. The remaining portion of the equality is written in the numerator in the resultant conversion factor.
The unit that results upon the cancelation of "kilograms of lead" is "g Pb," which is not the desired final unit. As a result, the atomic weight equality must be applied as a second conversion factor. In order to completely eliminate the unit "g Pb," the quantity on the right side of the atomic weight equality becomes the denominator in the second conversion factor that is applied to solve the given problem. The remaining portion of this equality is written in the numerator in the resultant conversion factor, as shown below.
\( {\text {0.98}}\) \({\cancel{\rm{kg} \; \rm{Pb}}} \times\) \( \dfrac{1,000\; \bcancel{\rm{g} \; \rm{Pb}}}{ \; \cancel{\rm{kg} \; \rm{Pb}}}\) × \( \dfrac{1 \; \rm{mol} \; \rm{Pb}}{207.20\; \bcancel{\rm{g} \; \rm{Pb}}}\) = \( {\text {4.7297297297...}}\) \({\rm{mol} \; \rm{Pb}}\) ≈ \( {\text {4.7}}\) \({\rm{mol} \; \rm{Pb}}\)
The solution is calculated by multiplying the given number by the value in each numerator, and then dividing by the quantity in each denominator. When using a calculator, each conversion factor should be entered in parentheses, or the "=" key should be used after each division. Applying the correct number of significant figures to the calculated quantity results in the final answer that is shown above.
Consider a problem that requires a calculation of the mass of chromium that contains 4.14 × 1026 atoms of chromium.
- Identify the indicator information in the given problem, and state which molar standard is associated with each indicator.
- Write an equality pattern that corresponds to each of the indicators identified in Part (a).
- Using dimensional analysis, apply the equalities that were developed in Part (b) as conversion factors, in order to bring about the desired unit transformation and solve the given problem.
- Answer
- Indicator Information
The word "mass," coupled with the knowledge that chromium, Cr, is an element, indicates that a mass-based atomic weight equality should be developed and applied to solve this problem.
Additionally, the word "atoms" indicates that an Avogadro's number equality should be developed and applied to solve this problem.
Equality Patterns
Atomic Weight Equality Pattern
The word "mass," coupled with the knowledge that chromium, Cr, is an element, indicates that a mass-based atomic weight equality should be developed. Regardless of the specific indicator word that is present in the given problem, "grams" is used as the first unit on the right side of this type of equality. The chemical name that is referenced in the given statement, "chromium," should not be used in this, or any, equality. Instead, the corresponding elemental symbol, "Cr," is incorporated into the remaining unit positions in the equality that is being developed. Finally, the atomic mass average of chromium, Cr, is 51.966, based on the numerical value that is written underneath its elemental symbol on the periodic table. However, this value is recorded to the thousandths place, which exceeds the decimal place standard that was defined above. Therefore, when this value is inserted into the numerical position on the right side of an atomic weight equality, it must be rounded to the hundredths place, as shown below.1 mol Cr = 51.97 g Cr
Avogadro's Number Equality Pattern
The word "atoms" indicates that an Avogadro's number equality should also be developed. Furthermore, since "atoms" is an indicator word, this word is inserted as the second unit on the right side of this type of equality. As stated above, the chemical name that is referenced in the given statement, "chromium," should not be used in this, or any, equality. Instead, the corresponding elemental symbol, "Cr," is incorporated into both of the secondary unit positions in the equality that is being developed. The resultant Avogadro's number equality is shown below.1 mol Cr = 6.02 × 1023 Cr atoms
Because the given chemical information is an elemental name, the indicator word "atoms" appropriately corresponds to the chemical formula that is applied in this equality.
Dimensional Analysis
In order to completely eliminate the given unit, "atoms of chromium," a conversion factor based on the Avogadro's number equality must be applied first. Specifically, the quantity on the right side of this equality becomes the denominator in the first conversion factor that is applied to solve the given problem. While reversing the order of the two units on the right side of an Avogadro's number equality is not absolutely necessary, doing so more clearly illustrates the desired unit cancelation for this particular problem. The remaining portion of the equality is written in the numerator in the resultant conversion factor.
However, the unit that results upon the cancelation of "atoms of chromium" is "mol Cr," which is not the desired final unit. Therefore, the atomic weight equality must be applied as a second conversion factor. In order to completely cancel the intermediate unit of "mol Cr," the quantity on the left side of the atomic weight equality becomes the denominator in the second conversion factor that is applied to solve the given problem. The remaining portion of the equality is written in the numerator in the resultant conversion factor, as shown below.\( {4.14 \times 10^{26} \; \cancel{\rm{atoms} \; \rm{Cr}}} \times\) \( \dfrac{1 \; \bcancel{\rm{mol} \; \rm{Cr}}}{6.02 \times 10^{23} \; \cancel{\rm{atoms} \; \rm{Cr}}}\) × \( \dfrac{51.97 \; \rm{g} \; \rm{Cr}}{1 \; \bcancel{\rm{mol} \; \rm{Cr}}}\) = \( {\text {35,740.1661...}}\) \({\rm{g} \; \rm{Cr}}\) ≈ \( {\text {35,700}}\) \({\rm{g} \; \rm{Cr}}\)
The solution is calculated by multiplying the given number by the value in each numerator, and then dividing by the quantity in each denominator. When using a calculator, each conversion factor should be entered in parentheses, or the "=" key should be used after each division, and any quantity that is expressed in scientific notation should be offset by an additional set of parentheses. Applying the correct number of significant figures to the calculated quantity results in the final answer that is shown above.
Finally, note that this problem simply required a calculation of a "mass of chromium," and no particular unit was specified. Therefore, expressing the final answer in grams, as shown above, is acceptable. However, due to the large value of the calculated mass, reporting the solution as "35.7 kg Cr" would also be reasonable.

