1.6: Significant Figures in Calculations

Last updated
Save as PDF

Page ID: 213135

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Learning Objectives

Use significant figures correctly in mathematical operations.

It is important to be aware of significant figures when performing mathematical operations. For example, dividing 125 by 307 on a calculator gives 0.4071661238… to an infinite number of digits. However, not all of the digits in this answer have a practical meaning. Remember that calculators do not understand significant figures, and the person who is performing the calculation must apply the rules of significant figures to a result obtained from using a calculator.

When performing mathematical operations, there are two rules for limiting the number of significant figures in an answer, based on the operation being performed: One rule is applied for multiplication and division, and a different rule is applied for addition and subtraction.

In operations involving significant figures, the answer is reported in such a way that it reflects the reliability of the lowest quality value involved in the operation. In other words, an answer can be no more precise than the least precise number used to get that answer.

Multiplication and Division

For multiplication and division, the number of significant figures in each number being multiplied or divided must be counted, and the answer must be limited to the lesser count of significant figures. When comparing the number of digits that the answer should have to the number of digits that it actually has, three possible scenarios could arise. Specifically, if

the number of digits that the answer actually has is exactly equal to the number of digits that it should have, no adjustments need to be made, and the calculated answer is the final answer.
the number of digits that the answer actually has is less than the number of digits that it should have, significant zeroes must be added to the calculated answer, until it contains the correct number of significant figures.
the number of digits that the answer actually has is more than the number of digits that it should have, the calculated answer must be rounded.

Rounding

To round a number, the number of significant figures that the number should have must be known and are selected starting from the left-most digit in the calculated number. If the number immediately to the right of the last significant digit is less than 5, the value of the last significant digit remains the same and all subsequent digits are dropped. This is called rounding down. If the number immediately to the right of the last significant digit is greater than or equal to 5, the last significant digit is increased by 1 and all subsequent digits are again dropped. This is called rounding up. Regardless of whether a number is rounded up or down, the value of the final must remain approximately equal to that of the original, calculated number.

For example, consider the number "207.518". Right now, the measurement contains six significant figures. How would this number be rounded to have five significant figures? Four significant figures? Two significant figures? The answers, as well as the reasoning behind them, is outlined in Table \(\PageIndex{1}\).

Table \(\PageIndex{1}\): Rounding examples
Number of Significant Figures	Rounded Value	Reasoning
5	207.52	The left-most five digits are selected, and the last selected digit (1) is rounded up to a 2, since the next digit (8) is greater than 5.
4	207.5	The left-most four digits are selected, and the last selected digit (5) is rounded down to remain a 5, since the next digit (1) is less than 5.
2	210	The left-most two digits are selected, and the last selected digit (0) is rounded up to a 1, since the next digit (7) is greater than 5. However, the resultant value of "21" is not similar to "207.518". A non-significant ("placeholder") zero is added, as "210" is approximately equal to "207.518".

Scientific Notation

Remember that scientific notation provides a way of communicating significant figures without ambiguity, since all significant figures can simply be included in the coefficient. For example, the number 450 has two significant figures and would be written in scientific notation as 4.5 × 10², whereas 450.0 has four significant figures and would be written as 4.500 × 10². In scientific notation, all significant figures are listed explicitly.

A full multiplication example is shown below.

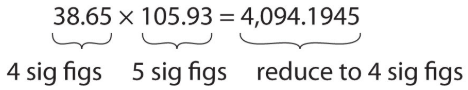
The first number involved in the calculation contains 4 significant figures, and the second number contains 5 significant figures. Therefore, final answer must be limited to 4 significant figures, and the digits "4,094" are selected to keep. Since the next digit (1) is less than 5, the number is rounded down and remains "4,094".

Addition and Subtraction

For addition and subtraction, the right-most significant digit in each number being added or subtracted must be selected, and the answer must be limited to the left-most of those options. When comparing the number of digits that the answer should have to the number of digits that it actually has, the same three scenarios that were considered for multiplication and division could arise.

For example, consider adding 1.2 and 4.41. The right-most significant digit in "1.2" is the "2", located in the tenths column, while the right-most significant digit in "4.41" is the "1" in the hundredths column. The answer would be limited to the tenths column, since the tenths column is further to the left, relative to the hundredths column. Since the next digit in the calculated answer (1) is less than 5, the last selected digit (6) is rounded down to remain a 6.

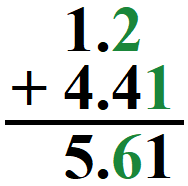
Addition SigFigs.png

Exercise \(\PageIndex{1}\)

Perform the following mathematical operations, expressing each answer with the appropriate number of significant figures.

217 ÷ 903.0 =
13.77 + 908.226 + 515 =

Answer a: Calculated answer: 0.240310075...
Correct answer: 0.240
Rationale: The operation being performed is division, so the number of significant digits in each given number must be counted. The first number involved in the calculation contains 3 significant figures, and the second number contains 4 significant figures. Therefore, the answer must be limited to 3 significant figures, and the digits "0.240" are selected to keep. (Note that the first zero is not significant, as it is before the first non-zero digit, so does not count toward the total number of selected digits.) Since the next digit (3) is less than 5, the number is rounded down and remains "0.240".
Answer b: Calculated answer: 1,436.996
Correct answer: 1,437
Rationale: The operation being performed is addition, so the right-most significant digit in each number being added must be selected. The right-most significant digit in the first number involved in the calculation is the final 7, in the hundredths place. The right-most significant digit in the second number involved in the calculation is the 6, in the thousandths place. The right-most significant digit in the third number involved in the calculation is the final 5, in the ones place. Therefore, the answer must be limited to the ones place, since the ones place is the furthest to the left of the relevant options. Since the next digit in the calculated answer (9) is greater than 5, the number is rounded up to become "1,437".

Calculations Involving Multiplication/Division and Addition/Subtraction

When performing calculations that involve either a multiplication or a division and an addition or a subtraction, the correct order of operations must be applied. Any operation written in parentheses must be performed first, followed by any multiplication and division. Addition and subtraction is performed last. Ideally, the significance of each intermediate answer would be mentally-determined, but ultimately only applied after performing the final calculation, because successive rounding can compound inaccuracies. When working on paper, however, it is often desirable to minimize the number of digits that must be written out. Therefore, in the worked examples in this text, the results of intermediate steps in a calculation will be shown to the correct number of significant figures allowed for that step, effectively treating each step as a separate calculation. This procedure is intended to reinforce the rules for determining the number of significant figures, but in some cases it may give a final answer that differs in the last digit from that obtained using a calculator, where all digits are carried through to the last step.