1.7: Temperature Units and Conversions
- Page ID
- 213153
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Identify the different scales used for measuring temperature.
- Apply equations to convert temperature units from one scale to another.
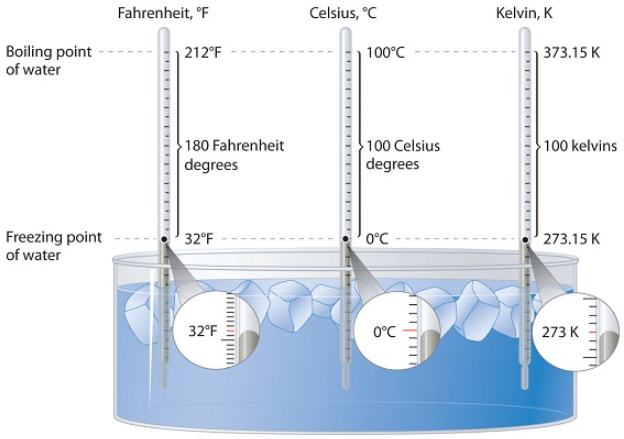
As defined previously, temperature (T) is a measure of how hot an object is. Three different scales are commonly used to measure temperature, degrees Fahrenheit, which is abbreviated as °F, degrees Celsius, °C, and Kelvin, K. Thermometers measure temperature by using materials that expand or contract when heated or cooled. Mercury or alcohol thermometers, for example, have a reservoir of liquid that expands when heated and contracts when cooled, so the liquid column lengthens or shortens as the temperature of the liquid changes.
The Fahrenheit Scale
The first thermometers were glass and contained alcohol, which expanded and contracted as the temperature changed. The Fahrenheit scale, used in the U.S. system of measurement, was first developed in 1724 by German scientist, Daniel Gabriel Fahrenheit, who used mercury in his thermometer tube. The main problem with this scale is the arbitrary definitions of temperature: The freezing point of water was defined as 32 °F and the boiling point as 212 °F. The Fahrenheit scale is typically not used for scientific purposes.
The Celsius Scale
The Celsius scale, used in the metric system of measurement, is named after Swedish astronomer Anders Celsius. The Celsius scale sets the freezing point and boiling point of water at 0 °C and 100 °C, respectively. The distance between those two points is divided into 100 equal intervals, each of which is one degree. Another term sometimes used for the Celsius scale is "centigrade" because there are 100 degrees between the freezing and boiling points of water on this scale. However, the preferred term is "Celsius".
The Kelvin Scale
The Kelvin scale, used in the SI system of measurement, is named after Scottish physicist and mathematician Lord Kelvin. It is based on molecular motion, with the temperature of 0 K, also known as absolute zero, being the temperature at which all molecular motion ceases. The freezing point of water on the Kelvin scale is 273.15 K, while its boiling point is 373.15 K. Notice that there is no "degree" used in a Kelvin temperature designation. Unlike the Fahrenheit and Celsius scales, in which temperatures are referred to as "degrees Fahrenheit" or "degrees Celsius", temperatures in the Kelvin scale are simply designated as "kelvins."
Converting between Temperature Scales
Temperatures are converted using equations, which must contain both an equal sign and a variable. When performing temperature conversions, using appropriately-formatted variables is important. The quantity that is being measured should be written as the primary variable, and any qualifiers or information about that quantity should be written as a subscript. For example, the phrase "temperature in degrees Celsius" should be written as "TC". A capital "T" should be used, as a lower-case "t" represents time. Simply using a capital "C" is not appropriate, as "C" does not refer to temperature at all, but rather to a quantity called "heat capacity."
Since the magnitude of one degree on the Kelvin scale is the same size as one degree on the Celsius scale, these measurements can be converted from one to the other using the equation that is shown below.
TK = TC + 273.15
The appropriate number of significant digits must be applied to the answer using addition and subtraction rules.
Degrees on the Fahrenheit scale, however, are based on an English tradition of using 12 divisions, just as 1 foot is divided into 12 inches. The following equation relates degrees Fahrenheit and degrees Celsius.
TF = 1.8TC + 32
Note that "1.8" and "32" are exact numbers and, therefore, do not impact the significance of the final answer. However, since multiple mathematical operations are involved in this equation, both multiplication and division rules and addition and subtraction rules must be applied, in order to report a scientifically-correct final answer.
When using these equations, the given value, which includes the number and its associated unit, replaces the relevant variable in the equation.
A student with a fever has a temperature of 103.5 °F. Express this temperature in degrees Celsius and Kelvin.
Solution
In order to convert from degrees Fahrenheit to degrees Celsius, the given information must be incorporated into the second equation that is shown above, as follows.
103.5 °F = 1.8TC + 32
Order of operations dictates that subtraction must occur first, followed by division, and the final answer is rounded to three significant figures.
TC = 39.7 °C
This answer can then be converted to Kelvin by inserting the calculated value into the first equation, as shown below. The final answer is rounded to the tenths place.
TK = 39.7 °C + 273.15
TK = 312.9 K
Convert the boiling point of gold, 3080. K, to degrees Celsius and degrees Fahrenheit.
- Answer
- In order to convert from Kelvin to degrees Celsius, the given information must be incorporated into the first equation that is shown above, as follows. The final answer is rounded to the ones place.
3080 K = TC + 273.15
This answer can then be converted to degrees Fahrenheit by inserting the calculated value into the second equation, as shown below.
TC = 2807 °CTF = 1.8(2807 °C) + 32
Order of operations dictates that multiplication must occur first, followed by addition, and the final answer is rounded to four significant figures.TF = 5,084 °F


