1.5: Significant Figures and the Quality of Measurements
- Page ID
- 213134
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Identify the number of significant figures in a reported value.
Taking Scientific Measurements
The significant figures in a measurement consist of all the certain digits in that measurement plus one uncertain or estimated digit. Certain digits are based on the specific graduations, or markings, that are visible on the tool being used to take the measurement. A tool with more graduations will result in a measurement with more significant figures. An uncertain digit is a guess, or estimate, of where the object falls between the nearest graduations. Therefore, in a correctly-reported measurement, the final digit is significant but not certain.
Using either ruler in illustration below, it is clear that the length of the object is between 2 and 3. The bottom ruler contains only whole-number markings. With that ruler, the tenths digit can be estimated and the length of the object may be reported as 2.5. However, another person may judge that the measurement is 2.4 or perhaps 2.6. Therefore, while the 2 is known for certain, the value of the tenths digit is uncertain. The measurement taken with the bottom ruler contains 2 significant figures, because the visible graduations allow for only a single certain digit , the 2, to be known, and one uncertain, or guessed, digit.
The top ruler contains marks that allow for certainty to the tenths place. Now the same object may be measured as 2.55. The measurer is capable of estimating the hundredths digit, because he can be certain that the tenths digit is a 5. Again, another measurer may report the length of the object to be 2.54 or 2.56. In this case, there are two certain digits, the 2 and the 5, with the hundredths digit being uncertain. The measurement taken with the top ruler contains 3 significant figures, because the visible graduations allow for a second certain digit to be known, and one uncertain digit must again be recorded. Because the top ruler allows for a measurement with an additional significant figure, the top ruler is a superior ruler for measuring lengths, relative to the bottom ruler.
With either ruler, it would not be possible to report the length at 2.553, as only one uncertain digit can be recorded for any measurement.

Use each diagram to report a measurement to the proper number of significant figures.
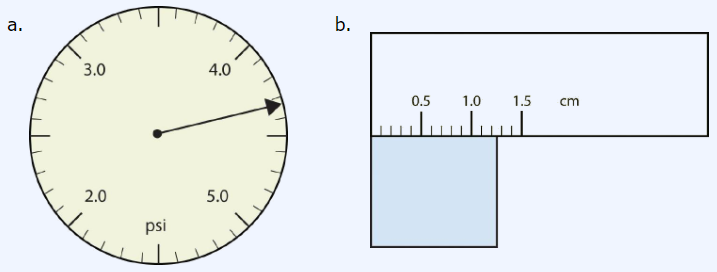
Solutions
Answer a: 4.33 psi
Explanation: The arrow is between 4.3 and 4.4, so the measurement must include "4.3" as certain digits. The next digit must be estimated. The arrow looks like about one-third of the way across the space, so the hundredths place can be estimated as a "3". Therefore, the measurement is reported to three significant figures. Finally, the unit on the tool is "psi," which is the abbreviation for "pounds per square inch" (a pressure unit).
Answer b: 1.25 cm
Explanation: The rectangle is between 1.2 and 1.3, so the measurement must include "1.2" as certain digits. The next digit must be estimated. The rectangle looks like about halfway across the space, so the hundredths place can be estimated as a "5". Therefore, this measurement is also reported to three significant figures. Finally, the unit on the tool is "cm."
Counting Significant Figures
When interpreting a reported measurement, it is necessary to be able to count the number of significant figures that it contains, without being able to view the tool that was used to take the measurement. The table below details the rules for determining the number of significant figures in a reported measurement.
| Rule | Examples |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
Give the number of significant figures in each, and identify the rule used for each conclusion.
- 5.87
- 0.031
- 52.90
- 0.2001
- 500
- 5.00 x 102
Solutions
Answer a: 3
Explanation: All three digits are significant, as they are all non-zero digits (Rule #1).
Answer b: 2
Explanation: The 3 and the 1 are significant (Rule #1). The leading zeros (written before the 3) are not significant (Rule #5).
Answer c: 4
Explanation: The 5, the 2, and the 9 are significant (Rule #1). The zero written after the 9 is also significant, because the number contains a written decimal point (Rule #4).
Answer d: 4
Explanation: The 2 and the 1 are significant (Rule #1). The leading zero (written before the 2) is not significant (Rule #5). The zeroes written between the 2 and the 1 are significant (Rule #3).
Answer e: 1
Explanation: The 5 is significant (Rule #1). The zeroes written after the 5 are not significant, because the number does not contain a written decimal point (Rule #6).
Answer f: 3
Explanation: This number is written in scientific notation. All of the digits in the coefficient (5, 0, and 0) are significant, but the numbers in the base ("x 10") and the power (2) are not.
Give the number of significant figures in each.
- 36.7 m
- 0.006140 s
- 804 kg
- 3,800 g
- Answer a
- Answer: 3
Explanation: All three digits are significant, as they are all non-zero digits (Rule #1). - Answer b
- Answer: 4
Explanation: The 6, the 1, and the 4 are significant (Rule #1). The leading zeroes (written before the 6) are not significant (Rule #5). The zero written after the 4 is significant, because the number contains a written decimal point (Rule #4). - Answer c
- Answer: 3
Explanation: The 8 and the 4 are significant (Rule #1). The zero written between the 8 and the 4 is also significant (Rule #3). - Answer d
- Answer: 2
Explanation: The 3 and the 8 are significant (Rule #1). The zeroes written after the 8 are not significant, because the number does not contain a written decimal point (Rule #6).
Exact Numbers
Integers obtained either by counting objects or from definitions are exact numbers, which are considered to have infinitely-many significant figures. If we have counted four objects, for example, then the number 4 has an infinite number of significant figures (i.e., it represents 4.000…). Similarly, 1 foot (ft) is defined to contain 12 inches (in), so both the "1" and the "12" would contain infinitely-many significant figures.

