6.5: Reactions of Monosaccharides
- Page ID
- 341508
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Distinguish between the oxidation and reduction of monosaccharides.
- Define what is meant by anomers.
- Predict the product of the ring formation of a monosaccharide.
Monosaccharide Redox Reactions
The chemical reactions of carbohydrates are largely that of the hydroxyl and carbonyl groups. The aldehyde and ketone groups in sugars undergo redox reactions to produce new substances. Recall, redox (reduction-oxidation) reactions involve a transfer of electrons. The substance losing electrons is said to undergo oxidation, while the substance gaining electrons is said to undergo reduction. In the case of organic molecules, this process is often distinguished based on the change in hydrogen and/or oxygen atoms. An increase in O and/or decrease in H represents oxidation. While a decrease in O and/or increase in H represents reduction. These processes result in a change in the carbonyl functional group present in the molecule Figure \(\PageIndex{1}\).
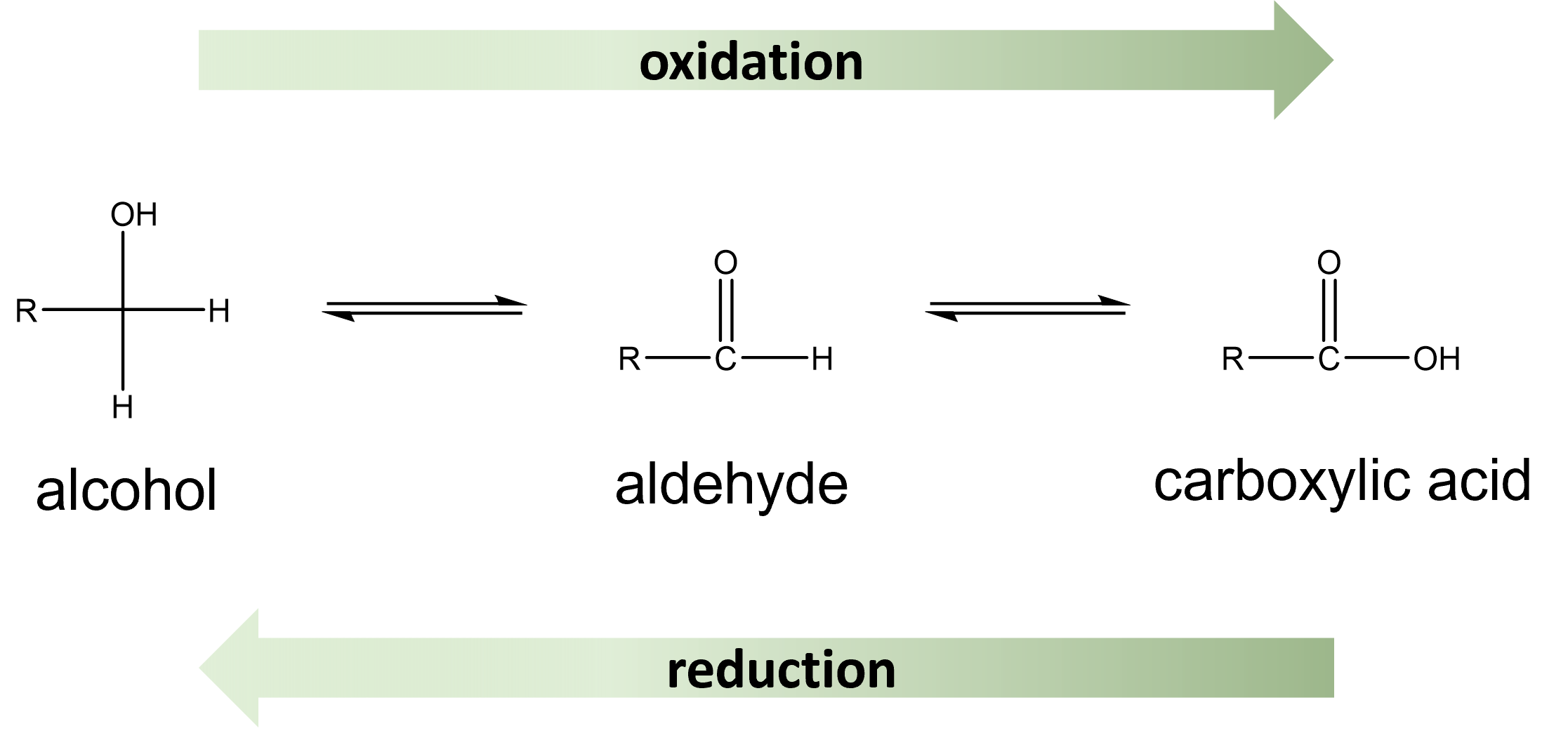
The oxidation of monosaccharides, results in the aldehyde functional group being converted into a carboxylic acid. This compound is then referred to as a sugar acid. The same process will occur if the monosaccharide is a ketose. In the presence of an oxidizing agent, the ketose can rearrange to an aldose and then undergo oxidation to form the sugar acid. Carbohydrates that are able to undergo oxidation are referred to as reducing sugars (sugars that are reducing agents). The Benedict's test is a useful test to determine the presence of reducing sugars. In the reaction between a reducing sugar and Benedict's reagent, copper (II) ion is reduced to copper (I) by the aldehyde functional group Figure \(\PageIndex{2}\):.

Figure \(\PageIndex{2}\): Chemical reaction for the reduction of Cu (II) by glucose. Note the oxidation of the aldehyde to a carboxylic acid.
The reduction of monosaccharides can also occur. This reaction results in the aldehyde functional group being converted to an alcohol, in a compound referred to as a sugar alcohol.

Monosaccharide Ring Formation
So far we have represented monosaccharides as linear molecules, but many of them also adopt cyclic structures. This conversion occurs because of the ability of aldehydes and ketones to react with alcohols. When the alcohol and aldehyde combine, a hemiacetal is formed. When an alcohol and ketone combine, a hemiketal is formed.
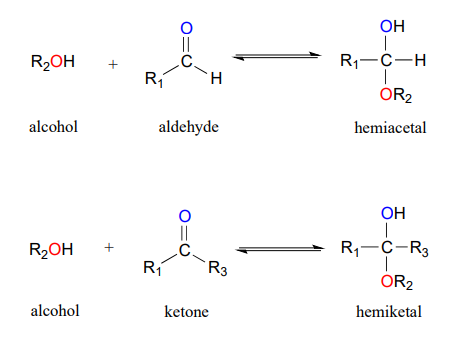
Figure \(\PageIndex{4}\): Formation of a hemiacetal and hemiketal. " Hemiacetals, Hemiketals, and Hydrates" by Tim Soderberg, LibreTexts is licensed under CC BY-NC-SA .
You might wonder why the aldehyde reacts with the OH group on the fifth carbon atom rather than the OH group on the second carbon atom next to it. Recall that cyclic alkanes containing five or six carbon atoms in the ring are the most stable. The same is true for monosaccharides that form cyclic structures: rings consisting of five or six carbon atoms are the most stable.
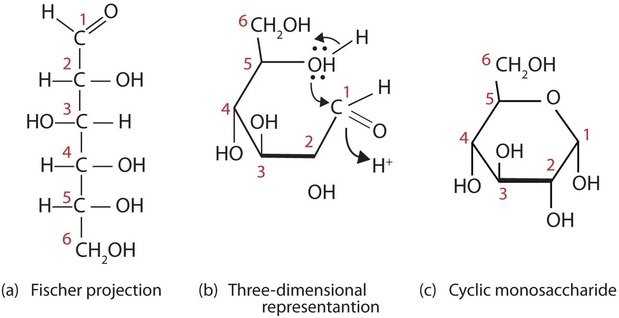
Figure \(\PageIndex{5}\): Ring formation of D-glucose. D-Glucose can be represented with a Fischer projection (a) or three dimensionally (b). By reacting the OH group on the fifth carbon atom with the aldehyde group, the cyclic monosaccharide (c) is produced.
When a straight-chain monosaccharide forms a cyclic structure, the carbonyl oxygen atom may be pushed either up or down, giving rise to two anomers. Anomers are a type of diastereomer (technically epimer) that differ only around the anomeric carbon. The anomeric carbon is the carbonyl carbon that reacts to form the cyclic structure. The two possible arrangements, termed anomers, are referred to as the alpha (α) and beta (β) anomers. The a anomer is formed when the hydroxyl group bonded to the anomeric carbon is trans (opposite side) to the carbon outside the ring (carbon 6). The β anomer is formed when the hydroxyl group bonded to the anomeric carbon is cis (same side) to the carbon outside the ring. Note that this hydroxyl group on the anomeric carbon is formed during the hemiacetal/hemiketal reaction.
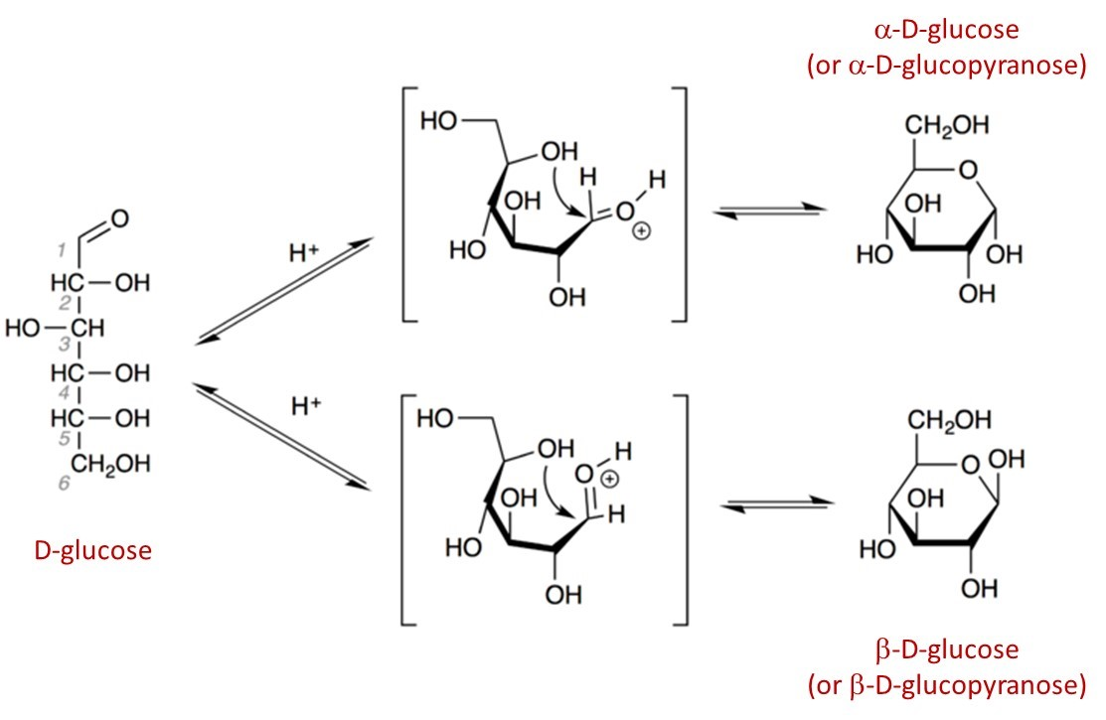
Figure \(\PageIndex{6}\): . Ring formation in D–glucose (left) to form α–D–glucose (top) and β–D–glucose (bottom). Steff-X, CC BY-SA 4.0 <https://creativecommons.org/licenses/by-sa/4.0>, via Wikimedia Commons (changes made to include molecule names).
It is possible to obtain a sample of crystalline glucose in which all the molecules have the α structure or all have the β structure. The α form melts at 146°C and has a specific rotation of +112°, while the β form melts at 150°C and has a specific rotation of +18.7°. When the sample is dissolved in water, however, a mixture is soon produced containing both anomers as well as the straight-chain form, in dynamic equilibrium (part (a) of Figure \(\PageIndex{7}\)). You can start with a pure crystalline sample of glucose consisting entirely of either anomer, but as soon as the molecules dissolve in water, they open to form the carbonyl group and then reclose to form either the α or the β anomer. The opening and closing repeats continuously in an ongoing interconversion between anomeric forms and is referred to as mutarotation (Latin mutare, meaning “to change”). At equilibrium, the mixture consists of about 36% α-D-glucose, 64% β-D-glucose, and less than 0.02% of the open-chain aldehyde form. The observed rotation of this solution is +52.7°.
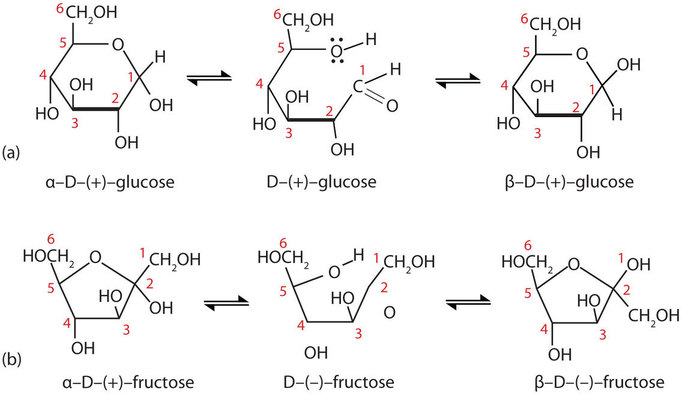
Figure \(\PageIndex{7}\): Monosaccharides. In an aqueous solution, monosaccharides exist as an equilibrium mixture of three forms. The interconversion between the forms is known as mutarotation, which is shown for D-glucose (a) and D-fructose (b).
Even though only a small percentage of the molecules are in the open-chain aldehyde form at any time, the solution will nevertheless exhibit the characteristic reactions of an aldehyde. As the small amount of free aldehyde is used up in a reaction, there is a shift in the equilibrium to yield more aldehyde. Thus, all the molecules may eventually react, even though very little free aldehyde is present at a time.
Drawing Cyclic Structures of Monosaccharides
The cyclic forms of sugars are commonly depicted as Haworth projections. This convention, first suggested by the Englis chemist Walter N. Haworth, shows molecules drawn as planar rings with darkened edges representing the side facing toward the viewer. The structure is simplified to show only the functional groups attached to the carbon atoms. Any group written to the right in a Fischer projection appears below (bottom face) the plane of the ring in a Haworth projection, and any group written to the left in a Fischer projection appears above (top face) the plane in a Haworth projection.

Figure \(\PageIndex{8}\): Conversion of the Fischer projection of D-glucose to the Haworth projection of ß-D-glucose.
- When converting a Fischer projection (line) to a Haworth projection, you must first identify the type of monosaccharide involved. If the carbohydrate represents an aldohexose, the pyranose ring is typically used. A pyranose is a cyclic structure that contains five carbon atoms and an oxygen. If the carbohydrate represents a ketohexose, the furanose ring is typically used. The furanose ring contains four carbon atoms and an oxygen.
.png?revision=1&size=bestfit&width=412&height=201)
Figure \(\PageIndex{9}\): Haworth projections of a pyranose and furanose ring.
- Indicate the arrangement of the hydroxyl group attached to the anomeric carbon to identify the sugar as an alpha or beta anomer. The α and β anomers are determined with respect to carbon 6. If the molecule represents a D-sugar, carbon 6 will be above the plane of the ring (top face) and forn an L-sugar, carbon 6 will be below the plane of the ring (ring). The α anomer occurs when the OH on the anomeric carbon is trans to carbon 6 and the β anomer occurs when the OH on the anomeric carbon is cis to carbon 6. If the cyclic structure contains a furanose, since carbon 1 is not included within the ring, that carbon group would be arranged in the opposite direction of the OH group (Figure \(\PageIndex{10}\)).
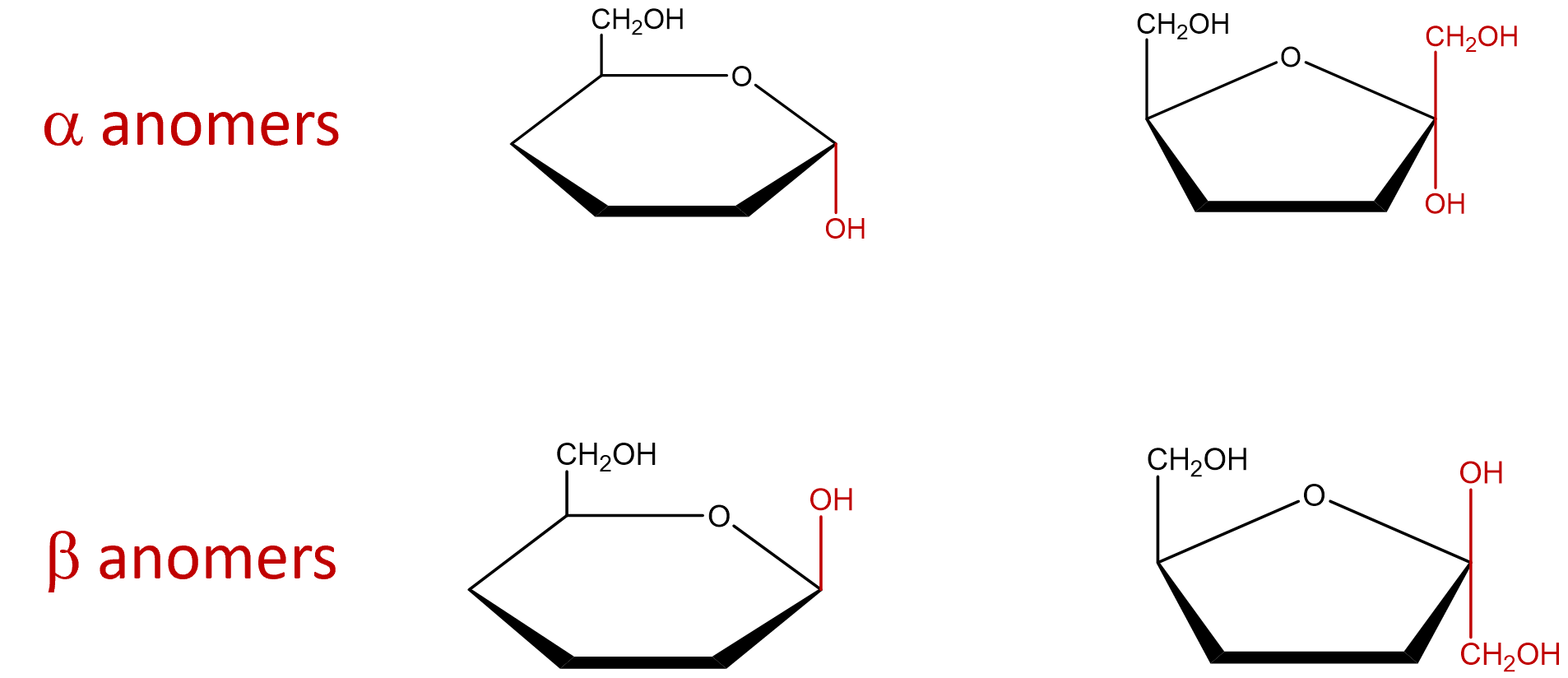
Figure \(\PageIndex{10}\): Arrangement of groups around the anomeric carbon to designate the molecule as an alpha or beta anomer.
-
The remaining chiral centers (carbons 2, 3 and 4 of the pyranose or carbons 3 and 4 of the furanose) are arranged based on the directions of the hydroxyl from the Fischer projection structures. Groups to the left of the Fischer projection would point up (top face), while groups to the right would point down (bottom face).
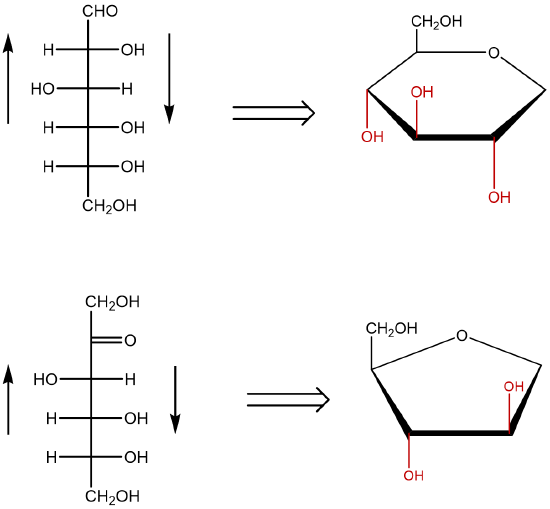
Figure \(\PageIndex{11}\): Fischer projections (left) and incomplete Haworth projections (right) of D-glucose (top) and D-fructose (bottom).
Since the Fischer Projection of any given carbohydrate is always the same, the Haworth Projection is essentially always the same. The only differences between the Haworth Projection of the alpha or beta form of a single carbohydrate, is how the OH (and carbon 1 if a furanose ring) is arranged around the anomeric carbon to determine whether the molecule is alpha or beta.
.png?revision=1&size=bestfit&width=480&height=461)
Figure \(\PageIndex{12}\): Haworth projections of D-glucose (top) and D-fructose (bottom).
The difference between the α and the β forms of sugars may seem trivial, but such structural differences are often crucial in biochemical reactions. This explains why we can get energy from the starch in potatoes and other plants but not from cellulose, even though both starch and cellulose are polysaccharides composed of glucose molecules linked together.
Example \(\PageIndex{1}\)
Draw the cyclic structure for β-D-galactose. Identify the anomeric carbon.
Solution
.png?revision=1&size=bestfit&width=212&height=120)
To identify the structure, we should first start with the Fischer projection of D-galactose. Since it is an aldohexose, we will start with the pyranose ring. The beta anomer was requested, so the OH on the anomeric carbon (C1) is cis to C6. Since C6 is top face (pointing up), the OH will be top face. Carbons 2, 3, and 4 are then arranged based on the Fischer projection arrangement at those carbons (C2 right, C3 left, and C4 left).
Exercise \(\PageIndex{1}\)
Draw the cyclic structure for α-D-galactose. Identify the anomeric carbon
Summary
-
Monosaccharides can be oxidized to produce sugar acids or reduced to form sugar alcohols.
-
Monosaccharides commonly exist in the cyclic form and are shown as Haworth projections.
-
Two cyclic stereoisomers can form from each straight-chain monosaccharide; these are known as anomers. The alpha (α) anomer is trans to carbon 6 and the beta (ß) anomer is cis to carbon 6.

