5.2: Energetics of Ionic Solids- Lattice Energy
- Page ID
- 326186
Lattice Energy
Many ionic compounds have simple structures. Because the forces holding the atoms together are primarily electrostatic, we can calculate the cohesive energy of the crystal lattice with good accuracy. Interesting questions to ask about these lattice energy calculations are:
- How accurate are lattice energy calculations?
- What do they teach us about the chemical bonds in ionic crystals?
- Can we use lattice energies to predict properties such as solubility, stability, and reactivity?
- Can we use lattice energies to predict the crystal structures of ionic compounds?
Let's start by looking at the forces that hold ionic lattices together. There are mainly two kinds of force that determine the energy of an ionic bond.
Electrostatic force
Electrostatic force is the attraction and repulsion between ions described by Coulomb's Law. Two ions with charges z+ and z-, separated by a distance r, experience a force F:
\[\mathbf{F} = -\frac{e^{2}}{4\pi \varepsilon_{0}} \frac{z_{+}z_{-}}{r^{2}}\]
where
e = 1.6022×10−19 C
4 π ε0 = 1.112×10−10 C²/(J m)
This force is attractive for ions of opposite charge and repulsive for ions of the same charge.
Closed-shell repulsion
When electrons in the core shells of one ion overlap with those of another ion, there is a repulsive force due to the Pauli exclusion principle. A third electron cannot enter an orbital that already contains two electrons. This force is short range, and is typically modeled as falling off exponentially or with a high power of the distance r between atoms. For example, in the Born approximation, B is a constant and ρ is a number with units of length, which is usually empirically determined from compressibility data. A typical value of ρ is 0.345 Å.
\[\mathbf{E}_{repulsion} = Bexp(\frac{-r}{\rho})\]
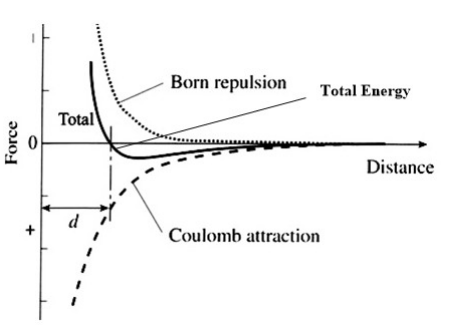
The energy of the ionic bond between two atoms is then calculated as the combination of net electrostatic and the closed-shell repulsion energies, as shown in Figure \(\PageIndex{2}\). Note that for the moment we are ignoring the attractive van der Waals forces between ions. For a pair of ions, the equilibrium distance between ions is determined by the minimum in the total energy curve.
Madelung Constant
We can use the above equations to calculate the lattice energy of a crystal by summing up the interactions between all pairs of ions. Because the closed-shell repulsion force is short range, this term is typically calculated only for interactions between neighboring ions. However, the Coulomb force is long range, and must be calculated over the entire crystal. This problem was first solved in 1918 by Erwin Madelung, a German physicist.
Figure \(\PageIndex{3}\): The Madelung constant is calculated by summing up electrostatic interactions with ion labeled 0 in the expanding spheres method. Each number designates the order in which it is summed. For example, ions labeled 1 represent the six nearest neighbors (attractive interaction), ions labeled 2 are the 12 next nearest neighbors (repulsive interaction) and so on.Consider an ion in the NaCl structure labeled "0" in Figure \(\PageIndex{3}\). We can see that the nearest neighbor interactions (+ -) with ions labeled "1" are attractive, the next nearest neighbor interactions (- - and + +) are repulsive, and so on. In the NaCl structure, counting from the ion in the center of the unit cell, there are 6 nearest neighbors (on the faces of the cube), 12 next nearest neighbors (on the edges of the cube), 8 in the next shell (at the vertices of the cube), and so on. Their distances from ion "0" increase progressively: ro, √2 ro, √3 ro, and so on, where ro is the nearest neighbor distance.
We can now write the electrostatic energy at ion "0" as:
\[\mathbf{E}_{elec} = -6\frac{e^{2}}{4\pi \varepsilon_{0}} \frac{z_{+}z_{-}}{r_{o}} + 12 \frac{e^{2}}{4 \pi \varepsilon_{0}} \frac{z_{+}z_{-}}{\sqrt{2}r_{o}} -8 \frac{e^{2}}{4 \pi \varepsilon_{0}} \frac{z_{+}z_{-}}{\sqrt{3}r_{o}} + \dots \]
Factoring out constants and the nearest-neighbor bond distance ro we obtain:
\[\mathbf{E}_{elec} = \frac{e^{2}}{4 \pi \varepsilon_{0}} \frac{z_{+}z_{-}}{r_{o}}(6 - \frac{12}{\sqrt{2}} + \frac{8}{\sqrt{3}} - \frac{6}{\sqrt{4}} + \dots) \]
Where the sum in parentheses, which is unitless, slowly converges to a value of A = 1.74756. Generalizing this formula for any three-dimensional ionic crystal we get a function:
\[\mathbf{E}_{elec} = \frac{e^{2}}{4 \pi \varepsilon_{0}} \frac{z_{+}z_{-}}{r_{o}} NA\]
where N is Avogadro's number (because we are calculating energy per mole of ions) and A is called the Madelung constant. The Madelung constant depends only on the geometrical arrangement of the ions and so it varies between different types of crystal structures, but within a given structure type it does not change. Thus MgO and NaCl have the same Madelung constant because they both have the NaCl structure.
|
|
|
|
A : C | Type |
|---|---|---|---|---|
| NaCl | NaCl | 1.74756 | 6 : 6 | Rock salt |
| CsCl | CsCl | 1.76267 | 6 : 6 | CsCl type |
| CaF2 | Cubic | 2.51939 | 8 : 4 | Fluorite |
| CdCl2 | Hexagonal | 2.244 | 6 : 3 | |
| MgF2 | Tetragonal | 2.381 | ||
| ZnS (wurtzite) | Hexagonal | 1.64132 | 4 : 4 | Wurtzite |
| TiO2 (rutile) | Tetragonal | 2.408 | 6 : 3 | Rutile |
| bSiO2 | Hexagonal | 2.2197 | ||
| Al2O3 | Rhombohedral | 4.1719 | 6 : 4 | Corundum |
|
A is the number of anions coordinated to cation and C is the numbers of cations coordinated to anion. |
||||
Born–Landé Equation
There are other factors to consider for the evaluation of lattice energy and the treatment by Max Born and Alfred Lande led to the formula for the evaluation of lattice energy for a mole of crystalline solid. The Born–Landé equation (Equation \(\ref{21.5.6}\)) is a means of calculating the lattice energy of a crystalline ionic compound and derived from the electrostatic potential of the ionic lattice and a repulsive potential energy term
\[ U= \dfrac{N_A M Z^2e^2}{4\pi \epsilon_o r} \left( 1 - \dfrac{1}{n} \right) \label{21.5.6}\]
where
- \(N_A\) is Avogadro constant;
- \(M\) is the Madelung constant for the lattice
- \(z^+\) is the charge number of cation
- \(z^−\) is the charge number of anion
- \(e\) is elementary charge, 1.6022×10−19 C
- \(ε_0\) is the permittivity of free space
- \(r_0\) is the distance to closest ion
- \(n\) is the Born exponent that is typically between 5 and 12 and is determined experimentally. \(n\) is a number related to the electronic configurations of the ions involved (Table \(\PageIndex{3}\)).
| Atom/Molecule | n |
|---|---|
| He | 5 |
| Ne | 7 |
| Ar | 9 |
| Kr | 10 |
| Xe | 12 |
| LiF | 5.9 |
| LiCl | 8.0 |
| LiBr | 8.7 |
| NaCl | 9.1 |
| NaBr | 9.5 |
Example \(\PageIndex{1}\): \(\ce{NaCl}\)
Estimate the lattice energy for \(\ce{NaCl}\).
Solution
Using the values giving in the discussion above, the estimation is given by
\[\begin{align*} U_{NaCl} &= \dfrac{(6.022 \times 10^{23} /mol) (1.74756 ) (1.6022 \times 10 ^{-19})^2 (1.747558)}{ 4\pi \, (8.854 \times 10^{-12} C^2/m ) (282 \times 10^{-12}\; m)} \left( 1 - \dfrac{1}{9.1} \right) \nonumber \\[4pt] &= - 756 \,kJ/mol\nonumber \end{align*} \nonumber\]
Much more should be considered in order to evaluate the lattice energy accurately, but the above calculation leads you to a good start. When methods to evaluate the energy of crystallization or lattice energy lead to reliable values, these values can be used in the Born-Hable cycle to evaluate other chemical properties, for example the electron affinity, which is really difficult to determine directly by experiment.
