13.5: Vibrational Overtones
- Page ID
- 63744
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Although the harmonic oscillator proves useful at lower energy levels, like \(v=1\), it fails at higher numbers of \(v\), failing not only to properly model atomic bonds and dissociations, but also unable to match spectra showing additional lines than is accounted for in the harmonic oscillator model.
Anharmonicity
Until this point, we have been using the harmonic oscillator to describe the internuclear potential energy of the vibrational motion. Fundamental vibrational frequencies of a molecule corresponds to transition from \(\Delta v= \pm 1\). While this is a decent approximation, bonds do not behave like they do in the Harmonic Oscillator approximation (Figure 13.5.1 ). For exaple, unlike the parabola given in the Harmonic Oscillator approximation, atoms that are too far apart will dissociate.
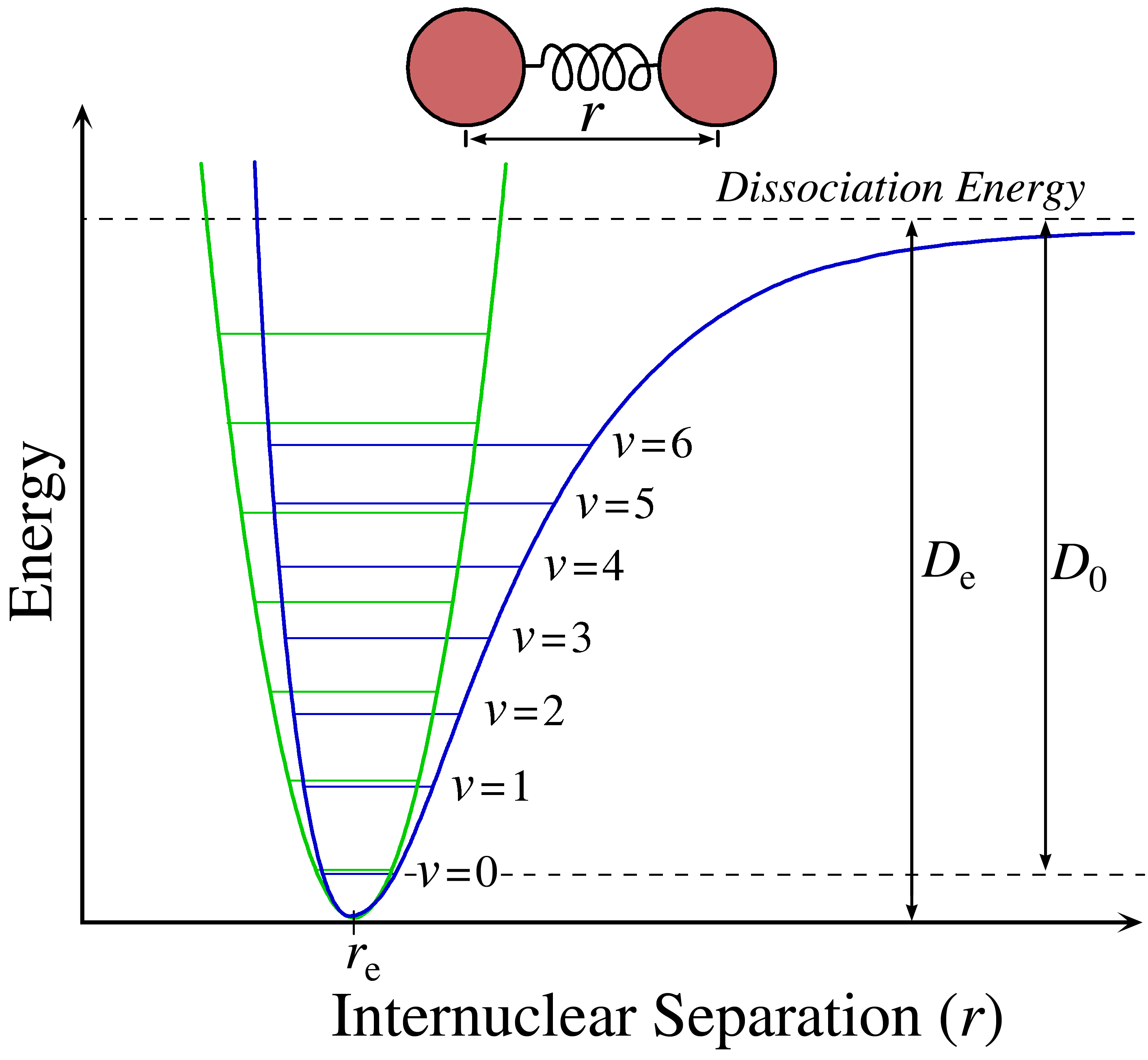
As you can see in Figure 13.5.1 , the harmonic oscillator potential (in green) well only roughly fits over the more accurate anharmonic oscillator well (in blue). The solid line accounts for dissociation at large R values, which the dotted lines does not even remotely cover. However, this is just one important difference between the harmonic and anharmonic (real) oscillators.
The real potential energy can be expanded in the Taylor series.
\[ V(R) = V(R_e) + \dfrac{1}{2!}\left(\dfrac{d^2V}{dR^2}\right)_{R=R_e} (R-R_e)^2 + \dfrac{1}{3!}\left(\dfrac{d^3V}{dR^3}\right)_{R=R_e} (R-R_e)^3 + \dfrac{1}{4!}\left(\dfrac{d^4V}{dR^4}\right)_{R=R_e} (R-R_e)^4 + ... \label{taylor} \]
This expansion was discussed in detail previously. The first term in the expansion is ignored since the derivative of the potential at \(R_e\) is zero (i.e., at the bottom of the well). The Harmonic Oscillator approximation only uses the next term, the quadratic term, in the series
\[V_{HO}(R) \approx V(R_e) + \dfrac{1}{2!}\left(\dfrac{d^2V}{dR^2}\right)_{R=R_e} (R-R_e)^2 \nonumber \]
or in terms of a spring constant (and ignore the absolute energy term) and defining \(r\) to equal the displacement from equilibrium (\(r=R-R_e\)), then we get the "standard" harmonic oscillator potential:
\[V_{HO}(R) = \dfrac {1}{2} kr^2 \nonumber \]
Alternatively, the expansion in Equation \(\ref{taylor}\) can be shortened to the cubic term
\[V(x) = \dfrac {1}{2} kr^2 + \dfrac {1}{6} \gamma r^3 \label{cubic} \]
where
- \(V(x_0) = 0\), and \(r = R - R_0\).
- \(k\) is the harmonic force constant, and
- \(\gamma\) is the first (i.e., cubic) anharmonic term
It is important to note that this approximation is only good for \(R\) near \(R_0\).
The harmonic oscillator approximation and gives by the following energies:
\[ E_{v} = \tilde{\nu} \left (v + \dfrac{1}{2} \right) \nonumber \]
When cubic terms in the expansion (Equation \(\ref{cubic}\)) is included, then Schrödinger equation solved, using perturbation theory, gives:
\[ E_{v} = \tilde{\nu} \left (v + \dfrac{1}{2} \right) - \tilde{\chi_e} \tilde{\nu} \left (v + \dfrac{1}{2} \right)^2 \nonumber \]
where \( \tilde{\chi_e}\) is the anharmonicity constant. It is much smaller than 1, which makes sense because the terms in the Taylor series approach zero. This is why, although \(G(n)\) technically includes all of the Taylor series, we only concern ourselves with the first and second terms. The rest are so small and barely add to the total and thus can be ignored. To get a more accurate approximation, more terms can be included, but otherwise, can be ignored. Almost all diatomics have experimentally determined \(\frac {d^2 V}{d x^2}\) for their lowest energy states. \(\ce{H2}\), \(\ce{Li2}\), \(\ce{O2}\), \(\ce{N2}\), and \(\ce{F2}\) have had terms up to \(n < 10\) determined of Equation \(\ref{taylor}\).
Overtones
The Harmonic Oscillator approximation predicts that there will be only one line the spectrum of a diatomic molecule, and while experimental data shows there is in fact one dominant line--the fundamental--there are also other, weaker lines. How can we account for these extra lines?
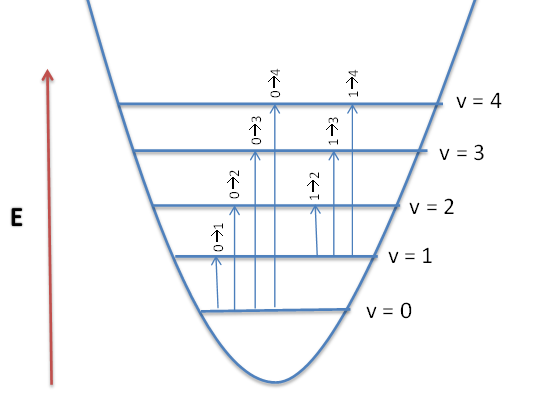
Any resonant frequency above the fundamental frequency is referred to as an overtone. In the IR spectrum, overtone bands are multiples of the fundamental absorption frequency. As you can recall, the energy levels in the Harmonic Oscillator approximation are evenly spaced apart. Energy is proportional to the frequency absorbed, which in turn is proportional to the wavenumber, the first overtone that appears in the spectrum will be twice the wavenumber of the fundamental. That is, first overtone \(v = 1 \rightarrow 2\) is (approximately) twice the energy of the fundamental, \(v = 0 \rightarrow 1\).

The levels are not equally spaced, like in the harmonic oscillator, but decrease as \(v\) increases, until it ultimately converges, is implied by Figure 13.5.4 . Also as a result of anharmonicity, the \(\Delta v= \pm 1\) selection rule is no longer valid and \(v\) can be any number. This leads to the observation of higher order transitions, or overtones, which result from the transition of the ground state to higher energy levels.
For the anharmonic oscillator, the selection rule is \(\Delta V= \text{any number}\). That is, there are no selection rules (for state to state transitions)
Overtones occur when a vibrational mode is excited from \(v=0\) to \(v=2\) (the first overtone) or \(v=0\) to \(v=3\) (the second overtone). The fundamental transitions, \(v=\pm 1\), are the most commonly occurring, and the probability of overtones rapid decreases as \( \Delta v > \pm 1\) gets bigger. Based on the harmonic oscillator approximation, the energy of the overtone transition will be approximately \(v\) times the fundamental associated with that particular transition. The anharmonic oscillator calculations show that the overtones are usually less than a multiple of the fundamental frequency. Overtones are generally not detected in larger molecules.
This is demonstrated with the vibrations of the diatomic \(\ce{HCl}\) in the gas phase:
| Transition | ṽobs [cm-1] | ṽobs Harmonic [cm-1] | ṽobs Anharmonic [cm-1] |
|---|---|---|---|
| \( 0 \rightarrow 1 \) (fundamental) | 2885.9 | 2885.9 | 2,885.3 |
| \( 0 \rightarrow 2 \) (first overtone) | 5668.0 | 5771.8 | 5,665.0 |
| \( 0 \rightarrow 3 \) (second overtone) | 8347.0 | 8657.7 | 8,339.0 |
| \( 0 \rightarrow 4\) (third overtone) | 10 923.1 | 11 543.6 | 10,907.4 |
| \( 0 \rightarrow 5\) (fourth overtone) | 13 396.5 | 14 429.5 | 13,370 |
We can see from Table 13.5.1 that the anharmonic frequencies correspond much better with the observed frequencies, especially as the vibrational levels increase. Because the energy levels and overtones are closer together in the anharmonic model, they are also more easily reached. This means that there is a higher chance of that level possibly being occupied, meaning it can show up as additional, albeit weaker intensity lines (the weaker intensity indicates a smaller probability of the transition occuring).
\(\ce{HCl}\) has a fundamental band at 2885.9 cm−1 and an overtone at 5668.1 cm−1 Calculate \(\tilde{\nu}\) and \( \tilde{\chi_e} \).
Write out the Taylor series, and comment on the trend in the increasing terms. Using a test number \(x\), please add terms 3, 4, and 5, then compare this to term 2. How do they compare? We have seen that the anharmonic terms increase the accuracy of our oscillator approximation. Why don't we care so much about terms past the second?
References
- Infrared and Raman Spectra of Inorganic and Coordination Compounds. Part A: Theory and Applications in Inorganic Chemistry; Part B: Application in Coordination, Organometallic, and Bioinorganic Chemistry, 5th Edition (Nakamoto, Kazuo)
- Lyle McAfee Journal of Chemical Education 2000 77 (9), 1122
- Stuart, Barbara. Infrared Spectroscopy: Fundamentals and Applications. Wiley, 2004. Print.

