8.2: Shielding and Effective Nuclear Charge

Learning Objectives

• To understand the basics of electron shielding and penetration

For an atom or an ion with only a single electron, we can calculate the potential energy by considering only the electrostatic attraction between the positively charged nucleus and the negatively charged electron. When more than one electron is present, however, the total energy of the atom or the ion depends not only on attractive electron-nucleus interactions but also on repulsive electron-electron interactions. When there are two electrons, the repulsive interactions depend on the positions of both electrons at a given instant, but because we cannot specify the exact positions of the electrons, it is impossible to exactly calculate the repulsive interactions. Consequently, we must use approximate methods to deal with the effect of electron-electron repulsions on orbital energies. These effects are the underlying basis for the periodic trends in elemental properties that we will explore in this chapter.

Electron Shielding and Effective Nuclear Charge

If an electron is far from the nucleus (i.e., if the distance \(r\) between the nucleus and the electron is large), then at any given moment, many of the other electrons will be between that electron and the nucleus (Figure \(\PageIndex{1}\)). Hence the electrons will cancel a portion of the positive charge of the nucleus and thereby decrease the attractive interaction between it and the electron farther away. As a result, the electron farther away experiences an effective nuclear charge (\(Z_{eff}\)) that is less than the actual nuclear charge \(Z\). This effect is called electron shielding.

Figure \(\PageIndex{1}\): This image shows how inner electrons can shield outer electrons from the nuclear charge. (CC BY-SA 3.0; from NikNaks).

As the distance between an electron and the nucleus approaches infinity, \(Z_{eff}\) approaches a value of 1 because all the other (\(Z − 1\)) electrons in the neutral atom are, on the average, between it and the nucleus. If, on the other hand, an electron is very close to the nucleus, then at any given moment most of the other electrons are farther from the nucleus and do not shield the nuclear charge. At \(r ≈ 0\), the positive charge experienced by an electron is approximately the full nuclear charge, or \(Z_{eff} ≈ Z\). At intermediate values of \(r\), the effective nuclear charge is somewhere between 1 and \(Z\):

\[1 ≤ Z_{eff} ≤ Z.\]

Notice that \(Z_{eff} = Z\) only for hydrogen and only for helium are \(Z_{eff}\) and \(Z\) comparable in magnitude (Figure \(\PageIndex{2}\)).

Shielding

Shielding refers to the core electrons repelling the outer electrons, which lowers the effective charge of the nucleus on the outer electrons. Hence, the nucleus has "less grip" on the outer electrons insofar as it is shielded from them.

\(Z_{eff}\) can be calculated by subtracting the magnitude of shielding from the total nuclear charge and the effective nuclear charge of an atom is given by the equation:

\[ Z_{eff}=Z-S \label{4}\]

where \(Z\) is the atomic number (number of protons in nucleus) and \(S\) is the shielding constant. The value of \(Z_{eff}\) will provide information on how much of a charge an electron actually experiences.

We can see from Equation \ref{4} that the effective nuclear charge of an atom increases as the number of protons in an atom increases (Figure \(\PageIndex{2}\)). Therefore as we go from left to right on the periodic table the effective nuclear charge of an atom increases in strength and holds the outer electrons closer and tighter to the nucleus. As we will discuss later on in the chapter, this phenomenon can explain the decrease in atomic radii we see as we go across the periodic table as electrons are held closer to the nucleus due to increase in number of protons and increase in effective nuclear charge.

Figure \(\PageIndex{2}\): Relationship between the Effective Nuclear Charge Z_eff and the Atomic Number Z for the Outer Electrons of the Elements of the First Three Rows of the Periodic Table. Except for hydrogen, (\(Z_{eff}\) is always less than \(Z\), and (\(Z_{eff}\) increases from left to right as you go across a row.

The shielding constant can be estimated by totaling the screening by all electrons (\(n\)) except the one in question.

\[ S = \sum_{i}^{n-1} S_i \label{2.6.0}\]

where \(S_i\) is the shielding of the i^th electron.

Electrons that are shielded from the full charge of the nucleus experience an effective nuclear charge (\(Z_{eff}\)) of the nucleus, which is some degree less than the full nuclear charge an electron would feel in a hydrogen atom or hydrogenlike ion.

From Equations \ref{4} and \ref{2.6.0}, \(Z_{eff}\) for a specific electron can be estimated is the shielding constants for that electron of all other electrons in species is known. A simple approximation is that all other electrons shield equally and fully:

\[S_i=1 \label{simple}\]

This crude approximation is demonstrated in Example \(\PageIndex{1}\).

Example \(\PageIndex{1}\): Fluorine, Neon, and Sodium

What is the effective attraction \(Z_{eff}\) experienced by the valence electrons in the three isoelectronic species: the fluorine anion, the neutral neon atom, and sodium cation?

Solution

Each species has 10 electrons, and the number of nonvalence electrons is 2 (10 total electrons - 8 valence), but the effective nuclear charge varies because each has a different atomic number \(A\). This is an application of Equations \ref{4} and \ref{2.6.0}. We use the simple assumption that all electrons shield equally and fully the valence electrons (Equation \ref{simple}).

The charge \(Z\) of the nucleus of a fluorine atom is 9, but the valence electrons are screened appreciably by the core electrons (four electrons from the 1s and 2s orbitals) and partially by the 7 electrons in the 2p orbitals.

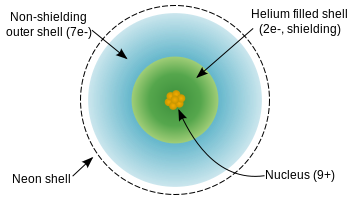
Diagram of a fluorine atom showing the extent of effective nuclear charge. (CC BY-SA- 3.0; from NikNaks).

• \(Z_\mathrm{eff}(\mathrm{F}^-) = 9 - 2 = 7+\)
• \(Z_\mathrm{eff}(\mathrm{Ne}) = 10 - 2 = 8+\)
• \(Z_\mathrm{eff}(\mathrm{Na}^+) = 11 - 2 = 9+\)

So the sodium cation has the greatest effective nuclear charge. This also suggests that \(\mathrm{Na}^+\) has the smallest radius of these species and that is correct.

Exercise \(\PageIndex{1}\): Magnesium Species

What is the effective attraction \(Z_{eff}\) experienced by the valence electrons in the magnesium anion, the neutral magnesium atom, and magnesium cation? Use the simple approximation for shielding constants in Equations \ref{4} and \ref{2.6.0}.

Answer

• \(Z_\mathrm{eff}(\mathrm{Mg}^-) = 12 - 10 = 2+\)
• \(Z_\mathrm{eff}(\mathrm{Mg}) = 12 - 10 = 2+\)
• \(Z_\mathrm{eff}(\mathrm{Mg}^+) = 12 - 10 = 2+\)

Remember that the simple approximations in Equations \ref{4} and \ref{2.6.0} suggest that valence electrons do not shield other valence electrons. Therefore, each of these species has the same number of non-valence electrons and Equations \ref{4} and \ref{2.6.0} suggest the effective charge on each valence electron is identical for each of the three species. However, this is not correct!

The fact that these approximations are poor is suggested by the experimental Zeff value shown in Table \(\PageIndex{1}\) for Mg. The value is appreciably larger than the +2 estimated above. This indicates that a more complex model is needed to predict the experimental observed Zeff value. The ability of valence electrons to shield (or partially shield) other valence electrons (e.g., Si≠1) shows that the simple approximations used above overestimate the total shielding constant S. A more sophisticated model is needed.

Electron Penetration

The approximation in Equation \ref{simple} is a good first order description of electron shielding, but the actual \(Z_{eff}\) experienced by an electron in a given orbital depends not only on the spatial distribution of the electron in that orbital but also on the distribution of all the other electrons present. This leads to large differences in \(Z_{eff}\) for different elements, as shown in Figure \(\PageIndex{2}\) for the elements of the first three rows of the periodic table.

Penetration describes the proximity to which an electron can approach to the nucleus. In a multi-electron system, electron penetration is defined by an electron's relative electron density (probability density) near the nucleus of an atom (Figure \(\PageIndex{3}\)). Electrons in different orbitals have different electron densities around the nucleus. In other words, penetration depends on the shell (\(n\)) and subshell (\(l\)).

For example, a 1s electron (Figure \(\PageIndex{3}\); purple curve) has greater electron density near the nucleus than a 2p electron (Figure \(\PageIndex{3}\); red curve) and has a greater penetration. This related to the shielding constants since the 1s electrons are closer to the nucleus than a 2p electron, hence the 1s screens a 2p electron almost perfectly (\(S=1\). However, the 2s electron has a lower shielding constant (\(S<1\) because it can penetrate close to the nucleus in the small area of electron density within the first spherical node (Figure \(\PageIndex{3}\); green curve). In this way the 2s electron can "avoid" some of the shielding effect of the inner 1s electron.

Figure \(\PageIndex{3}\): Orbital Penetration. A comparison of the radial probability distribution of the 2s and 2p orbitals for various states of the hydrogen atom shows that the 2s orbital penetrates inside the 1s orbital more than the 2p orbital does. Consequently, when an electron is in the small inner lobe of the 2s orbital, it experiences a relatively large value of \(Z_{eff}\), which causes the energy of the 2s orbital to be lower than the energy of the 2p orbital.

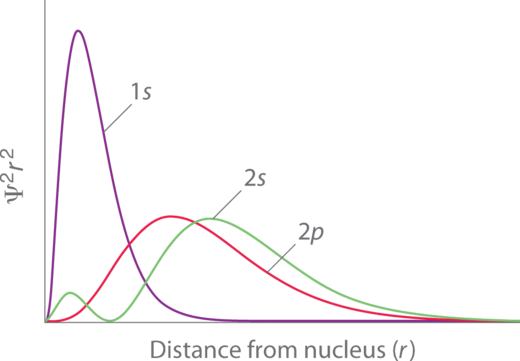
For the same shell value (\(n\)) the penetrating power of an electron follows this trend in subshells (Figure \(\PageIndex{3}\)):

\[s > p > d \approx f. \label{better1}\]

for different values of shell (n) and subshell (l), penetrating power of an electron follows this trend:

\[\ce{1s > 2s > 2p > 3s > 3p > 4s > 3d > 4p > 5s > 4d > 5p > 6s > 4f ...} \label{better2}\]

Penetration

Penetration describes the proximity of electrons in an orbital to the nucleus. Electrons that have greater penetration can get closer to the nucleus and effectively block out the charge from electrons that have less proximity.

Table \(\PageIndex{1}\): Effective Nuclear Charges for Selected Atoms

Atom	Sublevel	Z	Zeff
H	1s	1	1
He	1s	2	1.69
Li	1s, 2s	3	2.69, 1.28
Be	1s, 2s	4	3.68, 1.91
B	1s, 2s, 2p	5	4.68, 2.58, 2.42
F	1s, 2s, 2p	9	8.65, 5.13, 5.10
Na	1s, 2s, 2p, 3s	11	10.63, 6.57, 6.80, 2.51

Data from E. Clementi and D. L. Raimondi; The Journal of Chemical Physics 38, 2686 (1963).

Because of the effects of shielding and the different radial distributions of orbitals with the same value of n but different values of l, the different subshells are not degenerate in a multielectron atom. For a given value of n, the ns orbital is always lower in energy than the np orbitals, which are lower in energy than the nd orbitals, and so forth. As a result, some subshells with higher principal quantum numbers are actually lower in energy than subshells with a lower value of n; for example, the 4s orbital is lower in energy than the 3d orbitals for most atoms.

A Better Estimation of Shielding: Slater Rules

The concepts of electron shielding, orbital penetration and effective nuclear charge were introduced above, but we did so in a qualitative manner (e.g., Equations \ref{better1} and \ref{better2}). A more accurate model for estimating electron shielding and corresponding effective nuclear charge experienced is Slater's Rules. However, the application of these rules is outside the scope of this text.

Summary

The calculation of orbital energies in atoms or ions with more than one electron (multielectron atoms or ions) is complicated by repulsive interactions between the electrons. The concept of electron shielding, in which intervening electrons act to reduce the positive nuclear charge experienced by an electron, allows the use of hydrogen-like orbitals and an effective nuclear charge (\(Z_{eff}\)) to describe electron distributions in more complex atoms or ions. The degree to which orbitals with different values of l and the same value of n overlap or penetrate filled inner shells results in slightly different energies for different subshells in the same principal shell in most atoms.