6.1: Energy, Heat and Work
- Page ID
- 169990
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Energy, Heat and Work
Energy is the ability to move an object against a resisting force. Moving an object against a resisting force is called work, so we can write our energy definition more formally:
Energy is the ability to do work.
Work is a way to transfer energy from one collection of matter to another. For example, if you lift a backpack, you transfer some of your body’s energy to the backpack. You have less energy after you lift the backpack (you can’t keep lifting the backpack forever), but the backpack has more energy after it is lifted.
Energy can be used to do work, but it can also do things that do not involve motion and resistance. For example, think about a mixture of gasoline and oxygen. This mixture can do a great deal of work if we put it into an engine and then ignite it; that is what happens in an automobile engine. However, we can also simply ignite the mixture in an open beaker; no useful work is done in this case, but the beaker and everything else nearby will become very hot. In this case, the energy has been transferred in the form of heat. We now have two ways to transfer energy: heat and work. Here are formal definitions of these two terms:
Work occurs when energy is used to move an object against a resisting force.
Heat occurs when energy is used in any other way.
It’s worth pointing out that the words “work” and “heat” have somewhat different meanings in science than they do in everyday life. In everyday life, “work” can mean things like “doing your homework,” but in science, work requires motion. If you lift a heavy box, you do work, but if you just hold the heavy box over your head, you don’t (even though you get tired!). Likewise, in everyday life, when we speak of “heat” we usually mean thermal energy, the energy that a hot object possesses in greater quantity than a cool object. In science, “heat” is the transfer of energy from a warmer object to a cooler one. An object cannot contain heat, but it can lose or gain energy in the form of heat.
Units of Energy
In order to measure energy, we need a unit for it. In the metric system, the standard unit of energy is the joule. The formal definition of a joule is: A joule is the amount of energy expended when an object is moved 1 meter against a resisting force of 1 newton. (You can learn all about the concept of force in a physics class.) As for the joule, here are some statements that may help you visualize this unit. A joule is…
…enough energy to lift a one kilogram object 10.2 centimeters.
…enough energy to heat one milliliter of water from 20ºC to 20.24ºC.
…enough energy to keep a 60 watt light bulb glowing for 0.0167 seconds.
Obviously, a joule is a very small amount of energy, and in fact it is an inconveniently small amount when we describe chemical reactions. Chemists usually report energies for reactions in kilojoules (1 kJ = 1000 J).
Sign Conventions for Heat and Work
Heat and work have signs (positive or negative), and the sign of each depends on whether the system we are considering is gaining or losing energy. In this class, if a process makes the system gain energy, \(q\) and/or \(w\) are positive; if the process makes the system lose energy, \(q\) and/or \(w\) are negative. We can put this information into four formal statements:
- If heat flows into a system, \(q\) is positive.
- If heat flows out of a system, \(q\) is negative
- If the surroundings do work on the system, \(w\) is positive.
- If the system does work, \(w\) is negative.
Note that chemists use these conventions so the signs of \(q\) and \(w\) correspond the the energy changes of the system. If you were instead focused on the energy transferred in or out of the surroundings, you might opt to use the opposite sign conventions. Indeed, many physics and engineering courses choose different sign conventions!
Heat in Physical Processes
When we add energy to an object in the form of heat, the most common results are:
a) The temperature of the object goes up.
b) The object melts (if it is a solid) or boils (if it is a liquid).
Heat and Change in Temperature
When the temperature of an object changes, the relationship between the temperature change and the heat that the object gained or lost is:
\[q = mc\Delta T\]
Here, \(q\) stands for heat (in joules), m is the mass of the object that changes temperature (in grams), \(c\) is the specific heat capacity (or just “specific heat”) of the object, and \(\Delta T\) is the temperature change (in ºC). The specific heat capacity is essentially a conversion factor that relates energy to temperature changes and masses. Every substance has its own specific heat capacity, which depends on the chemical composition of the substance, the state of the substance, and (to some extent) the temperature of the substance. Here are specific heat capacities for the three states of water and for a few other common substances.
| Substance | Specific Heat Capacity (\(J/g^oC\)) | Substance | Specific Heat Capacity (\(J/g^oC\)) | |
|---|---|---|---|---|
| Water at 25ºC | 4.180 J/g·ºC | Helium (He) at 25ºC | 5.193 J/g·ºC | |
| Water at 0ºC | 4.218 J/g·ºC | Alcohol (C2H5OH) at 25ºC | 2.419 J/g·ºC | |
| Ice at 0ºC | 2.050 J/g·ºC | Salt (NaCl) at 25ºC | 0.864 J/g·ºC | |
| Steam at 100ºC | 2.042 J/g·ºC | Gold (Au) at 25ºC | 0.129 J/g·ºC |
Note that the specific heat capacity of water doesn’t change very much over the range 0ºC to 25ºC, but it changes a great deal when we convert the water into ice or steam. Note also that we see a wide range of specific heats when we look at a variety of chemicals; the specific heat of helium is about 40 times as large as that of gold.
Exercise \(\PageIndex{1}\): Calculating Energy Required for a Temperature Change
How much energy is required to increase the temperature of a 15.0 g sample of gold from \(20.0^oC\) to \(27.3^oC\)?
Solution
\[q_{gold} = m_{gold} c_{gold} \Delta T_{gold} \nonumber\]
\[q_{gold} = (15.0 g)(0.129 J/g·ºC)(27.3^oC - 20^oC)\nonumber\]
\[q_{gold} = 14.1255 J = 14.1 J\nonumber\]
Heat and Change in Physical State
So far, we have discussed heat transfers that cause temperature change. However, in a phase transition, heat transfer does not cause any temperature change.
For an example of phase changes, consider the addition of heat to a sample of ice at \(-20^oC\) (Figure \(\PageIndex{4}\)) and atmospheric pressure. The temperature of the ice rises linearly, absorbing heat at a constant rate of until it reaches \(0^oC\). Once at this temperature, the ice begins to melt and continues until it has all melted, absorbing 333 J/g of heat. The temperature remains constant at \(0^oC\) during this phase change. Once all the ice has melted, the temperature of the liquid water rises, absorbing heat at a new constant rate. At \(100^oC\) the water begins to boil. The temperature again remains constant during this phase change while the water absorbs 2256 kJ/kg of heat and turns into steam. When all the liquid has become steam, the temperature rises again, absorbing heat at a constant rate. If we started with steam and cooled it to make it condense into liquid water and freeze into ice, the process would exactly reverse, with the temperature again constant during each phase transition.
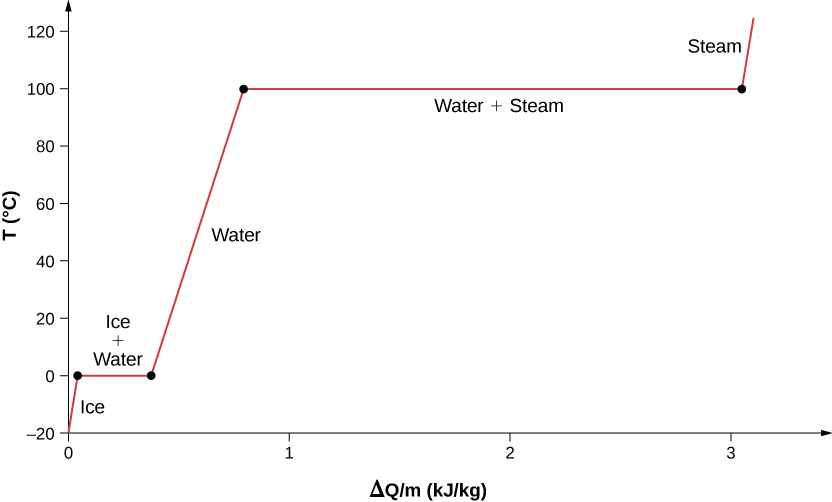
Figure \(\PageIndex{4}\): Temperature versus heat. The system is constructed so that no vapor evaporates while ice warms to become liquid water, and so that, when vaporization occurs, the vapor remains in the system. The long stretches of constant temperatures at \(0^oC\) and \(100^oC\) reflect the large amounts of heat needed to cause melting and vaporization, respectively.
Where does the heat added during melting or boiling go, considering that the temperature does not change until the transition is complete? Energy is required to melt a solid, because the attractive forces between the molecules in the solid must be broken apart, so that in the liquid, the molecules can move around at comparable kinetic energies; thus, there is no rise in temperature. Energy is needed to vaporize a liquid for similar reasons. Conversely, work is done by attractive forces when molecules are brought together during freezing and condensation. That energy must be transferred out of the system, usually in the form of heat, to allow the molecules to stay together (Figure \(\PageIndex{4}\)). Thus, condensation occurs in association with cold objects—the glass in Figure \(\PageIndex{5}\), for example.

Figure \(\PageIndex{5}\): Condensation forms on this glass of iced tea because the temperature of the nearby air is reduced. The air cannot hold as much water as it did at room temperature, so water condenses. Energy is released when the water condenses, speeding the melting of the ice in the glass. (credit: Jenny Downing)
The energy released when a liquid freezes is used by orange growers when the temperature approaches \(0^oC\). Growers spray water on the trees so that the water freezes and heat is released to the growing oranges. This prevents the temperature inside the orange from dropping below freezing, which would damage the fruit (Figure \(\PageIndex{6}\)).

Figure \(\PageIndex{6}\): The ice on these trees released large amounts of energy when it froze, helping to prevent the temperature of the trees from dropping below \(0^oC\). Water is intentionally sprayed on orchards to help prevent hard frosts. (credit: Hermann Hammer)
The energy per unit mass required to change a substance from the solid phase to the liquid phase, or released when the substance changes from liquid to solid, is known as the heat of fusion,\(\Delta H_{fus}\). The energy per unit mass required to change a substance from the liquid phase to the vapor phase is known as the heat of vaporization \(\Delta H_{vap}\). The strength of the forces depends on the nature of constituent particles of the substance. The heat \(q\) required in a phase change in a sample of mass m is given by
\[q = m\Delta H_{fus}\]
\[q = m\Delta H_{vap}\]
where these "heats of transition,"\(\Delta H_{fus}\) and \(\Delta H_{vap}\) are constants that are determined experimentally. Note that these heats of transformation are also sometimes called "latent heats". These constants are “latent,” or hidden, because during the phase changes, energy enters or leaves a system without causing a temperature change (!) in the system, so in effect, the energy is hidden.
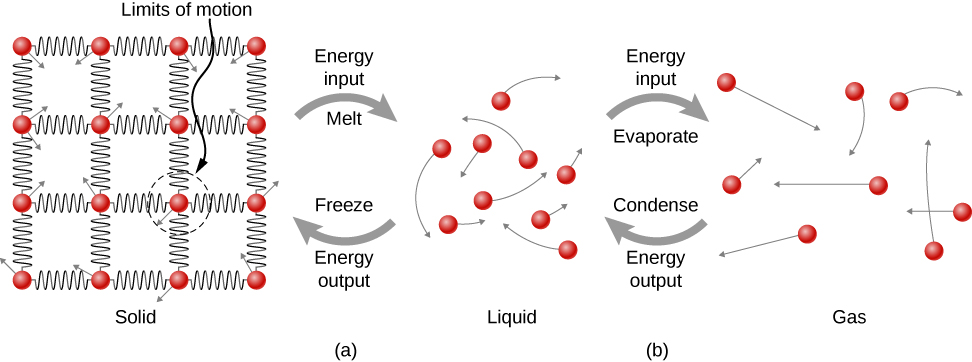
Figure \(\PageIndex{7}\): (a) Energy is required to partially overcome the attractive forces (modeled as springs) between particles in a solid to form a liquid. That same energy must be removed from the liquid for freezing to take place. (b) Particles become separated by large distances when going from liquid to vapor, requiring significant energy to completely overcome molecular attraction. The same energy must be removed from the vapor for condensation to take place.
Table \(\PageIndex{2}\) lists representative values of heats of phase transformation, together with melting and boiling points. Note that in general, \(L_v > L_f\). The table shows that the amounts of energy involved in phase changes can easily be comparable to or greater than those involved in temperature changes, as Figure \(\PageIndex{7}\) and the accompanying discussion also showed.
| Substance | Melting Point (\(^oC\)) | \(\Delta H_{fus}\), (\(J/g)\) | Boiling Point (\(^oC\)) | \(\Delta H_{vap}\) (\(J/g)\) |
|---|---|---|---|---|
| Mercury | –38.9 | 11.8 | 357 | 272 |
| Water | 0.00 | 334 | 100.0 | 2256[3] |
| Sulfur | 119 | 38.1 | 444.6 | 326 |
| Lead | 327 | 24.5 | 1750 | 871 |
| Antimony | 631 | 165 | 1440 | 561 |
| Aluminum | 660 | 380 | 2450 | 11400 |
| Silver | 961 | 88.3 | 2193 | 2336 |
| Gold | 1063 | 64.5 | 2660 | 1578 |
| Copper | 1083 | 134 | 2595 | 5069 |
| Values quoted at the normal melting and boiling temperatures at standard atmospheric pressure (\(1 \, atm\)). [2]Helium has no solid phase at atmospheric pressure. The melting point given is at a pressure of 2.5 MPa. [3]At \(37.0^oC\) (body temperature), the heat of vaporization for water is 2430 J/g. | ||||
Phase changes can have a strong stabilizing effect on temperatures that are not near the melting and boiling points, since evaporation and condensation occur even at temperatures below the boiling point. For example, air temperatures in humid climates rarely go above approximately \(38.0^oC\) because most heat transfer goes into evaporating water into the air. Similarly, temperatures in humid weather rarely fall below the dew point—the temperature where condensation occurs given the concentration of water vapor in the air—because so much heat is released when water vapor condenses.
More energy is required to evaporate water below the boiling point than at the boiling point, because the kinetic energy of water molecules at temperatures below \(100^oC\) is less than that at \(100^oC\), so less energy is available from random thermal motions. For example, at body temperature, evaporation of sweat from the skin requires a heat input of 2428 J/g, which is about 10% higher than the latent heat of vaporization at \(100^oC\). This heat comes from the skin, and this evaporative cooling effect of sweating helps reduce the body temperature in hot weather. However, high humidity inhibits evaporation, so that body temperature might rise, while unevaporated sweat might be left on your brow.
Note that heats of transformation can be expressed either in joules per gram or in joules per mole. For water, the heat of fusion is 3343.54 J/g. Since a mole of water equals 18.016 grams, the heat of fusion can also be expressed as 333.54 J/g x 18.016 g/mol = 60091 J/mol, or 6.009 kJ/mol.
Exercise \(\PageIndex{2}\): Calculating Energy Required for a Phase Change
How much energy is required to melt 35.0 g of ice at 0ºC?
Solution
\[q_{melting} = m\Delta H_{fus}\nonumber\]
\[q_{melting} = (35.0 g)(333.5 J/g)\nonumber\]
\[q_{melting} = 1.17x10^4 J = 11.7 kJ\nonumber\]
Like solid-liquid and and liquid-vapor transitions, direct solid-vapor transitions or sublimations involve heat. The energy transferred is given by the equation \(q = m\Delta H_{sub}\), where \(\Delta H_{sub}\) is the heat of sublimation, analogous to \(\Delta H_{fus}\) and \(\Delta H_{vap}\). The heat of sublimation at a given temperature is equal to the heat of fusion plus the heat of vaporization at that temperature.
We can now calculate any number of effects related to temperature and phase change. In each case, it is necessary to identify which temperature and phase changes are taking place. Keep in mind that heat transfer can cause both temperature and phase changes. Here is an example where we are changing both the temperature and the physical state.
Exercise \(\PageIndex{3}\): Heat Transfer Involving Both Temperature and Phase Change
Question:
How much heat is required to convert 50.0 g of ice at -10.0ºC into liquid water at 10.0ºC?
Solution:
We must put in enough heat to do three things: raise the temperature of the ice from -10.0ºC to 0ºC, melt the ice, and then raise the temperature of the resulting water from 0ºC to 10.0ºC:
Warming the ice: q1 = (50.0 g)(2.05 J/g·ºC)[0ºC – (-10.0ºC)] = 1025 J = 1.025 kJ
Melting the ice: q2 = (50.0 g)(333.5 J/g) = 16675 J = 16.675 kJ
Warming the liquid water: q3 = (50.0 g)(4.18 J/g·ºC)(10.0ºC – 0ºC) = 2090 J = 2.09 kJ
Total heat required: qtotal = q1 + q2 + q3 = 1.025 kJ + 16.675 kJ + 2.09 kJ = 19.8 kJ
From the above calculation, we see that a total of 19.8 kJ is required to convert 50.0 g of ice at -10.0ºC into liquid water at 10.0ºC
Exercise \(\PageIndex{4}\): Calculating Final Temperature from Phase Change
Question:
Three ice cubes are used to chill a soda at \(20^oC\) with mass \(m_{soda} = 250 \, g\). The ice is at \(0^oC\) and each ice cube has a mass of 6.0 g. Assume that the soda is kept in a foam container so that heat loss can be ignored and that the soda has the same specific heat as water. Find the final temperature when all ice has melted.
Strategy:
The ice cubes are at the melting temperature of \(0^oC\). Heat is transferred from the soda to the ice for melting. Melting yields water at \(0^oC\), so more heat is transferred from the soda to this water until the water plus soda system reaches thermal equilibrium. So, in order to solve this problem, we must consider three heat values:
1) Melting the ice at \(0^oC\):
\[q_1= m_{ice} \Delta H_{fus}.\nonumber\]
2) Warming the melted ice to the final equilibrium temperature:
\[q_2 = m_{ice}c_w (T_f - 0^oC).\nonumber\]
3) Cooling the soda to the final equilibrium temperature:
\[q_3 = m_{soda}c_w (T_f - 20^oC).\nonumber\]
Since no heat is lost, only transferred:
\[q_1 + q_2 + q_3 = 0,\nonumber\]
so that
\[m_{ice} \Delta H_{fus};+ m_{ice}c_w(T_f - 0^oC) + m_{soda}c_w (T_f - 20^oC) = 0\nonumber\]
Solve for the unknown quantity
\[T_f = \dfrac{m_{soda}c_w(20^oC) - m_{ice}\Delta H_{fus}}{(m_{soda} + m_{ice})c_w}\nonumber\]
Solution
First we identify the known quantities. The mass of ice is \(m_{ice} = 3 \times 6.0 \, g = 18 \, g\) and the mass of soda is \(m_{soda} = 250 \, g\). Then we calculate the final temperature:
\[T_f = \dfrac{20,930 \, J - 6012 \, J}{1122 \, J/^oC} = 13^oC\nonumber\]
Significance This example illustrates the large energies involved during a phase change. The mass of ice is about 7% of the mass of the soda but leads to a noticeable change in the temperature of the soda. Although we assumed that the ice was at the freezing temperature, this is unrealistic for ice straight out of a freezer: The typical temperature is \(-6^oC\). However, this correction makes no significant change from the result we found. Can you explain why?
Problem-Solving Strategy: The Effects of Heat Transfer
- Examine the situation to determine that there is a change in the temperature or phase. Is there heat transfer into or out of the system? When it is not obvious whether a phase change occurs or not, you may wish to first solve the problem as if there were no phase changes, and examine the temperature change obtained. If it is sufficient to take you past a boiling or melting point, you should then go back and do the problem in steps—temperature change, phase change, subsequent temperature change, and so on.
- Identify and list all objects that change temperature or phase.
- Identify exactly what needs to be determined in the problem (identify the unknowns). A written list is useful.
- Make a list of what is given or what can be inferred from the problem as stated (identify the knowns). If there is a temperature change, the transferred heat depends on the specific heat of the substance, and if there is a phase change, the transferred heat depends on the heat of transformation of the substance.
- Solve the appropriate equation for the quantity to be determined (the unknown).
- Substitute the knowns along with their units into the appropriate equation and obtain numerical solutions complete with units. You may need to do this in steps if there is more than one state to the process, such as a temperature change followed by a phase change. However, in a calorimetry problem, each step corresponds to a term in the single equation \(q_{released} + q_{absorbed} = 0\). Note that Exercise 4 is an example of such an equation.
- Check the answer to see if it is reasonable. Does it make sense? As an example, be certain that any temperature change does not also cause a phase change that you have not taken into account.
Exercise \(\PageIndex{2}\)
Why does snow often remain even when daytime temperatures are higher than the freezing temperature?
Snow is formed from ice crystals and thus is the solid phase of water. Because enormous heat is necessary for phase changes, it takes a certain amount of time for this heat to be transferred from the air, even if the air is above \(0^oC\)
Practice Problems Involving Heat
1) The specific heat of ethanol (C2H5OH) is 2.45 J/g·ºC, and its density is 0.789 g/mL. Using this information, answer the following questions:
a) How much heat is required to raise the temperature of 50.0 mL of ethanol from –5.0ºC to 25.0ºC?
b) If 525 J of heat is added to 25.0 g of ethanol, and the initial temperature of the ethanol is 10.0ºC, what will the final temperature be?
c) A 50.0 g sample of water is placed beside a sample of ethanol whose mass is unknown. The two samples then absorb equal amounts of heat. The temperature of the water increases from 20.0ºC to 28.7ºC, while the temperature of the ethanol increases from 20.0ºC to 31.3ºC. Calculate the mass of the ethanol.
2) Jerry puts a 71.325 g piece of aluminum into a beaker and adds 123.4 g water. How much heat will be required to raise the temperature of the water and the aluminum from 18.4ºC to 31.6ºC? You will need the following information:
Al: specific heat = 0.897 J/g·ºC in this temperature range
H2O: specific heat = 4.177 J/g·ºC in this temperature range
3) A chemist heats 31.5 g of NaCl crystals to 76.5ºC, and then pours the crystals into 61.2 g of CCl4. The initial temperature of the CCl4 is 12.8ºC, and the final temperature is 36.5ºC. The specific heat of CCl4 (carbon tetrachloride) is 0.751 J/g·ºC. Assuming that no energy is lost to the surroundings, calculate the specific heat of NaCl.
4) You put 12.0 g of ice at 0.0ºC into a coffee-cup calorimeter containing 50.0 g of water at 25.0ºC. Assuming that all the ice melts, determine the final temperature of the cup contents. You’ll need the following information for water:
melting point: 0.0 ºC specific heat capacity: 4.18 J/gºC heat of fusion: 333 J/g
5) A chunk of iron at 300.0ºC is added to an insulated container holding 100.0 g of water at 25.0 ºC. What is the minimum mass of iron required to convert all the water into steam at 100.0 ºC?
You’ll need the following information:
Water -- boiling point: 100.0 ºC specific heat capacity: 4.18 J/gºC heat of vaporization: 2260 J/g
Iron – specific heat capacity: 0.448 J/gºC
------------------------------------------------------------------------------
AnswerS to the Practice Problems Involving Heat
1) a) 2.90 kJ b) 18.6 °C c) 65.7 g
2) 7.65 x 103 J
3) 0.865 J/g°C
4) 4.7 °C
5) 2870 g

