Skip to main content
Chemistry LibreTexts

3.4.2.0: Valence Bond Theory and Hybrid Orbitals (Problems)

  1. Last updated
  2. Save as PDF
  • Page ID
    210714

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    PROBLEM \(\PageIndex{1}\)

    Explain how σ and π bonds are similar and how they are different.

    Answer

    Similarities: Both types of bonds result from overlap of atomic orbitals on adjacent atoms and contain a maximum of two electrons. Differences: σ bonds are stronger and result from end-to-end overlap and all single bonds are σ bonds; π bonds between the same two atoms are weaker because they result from side-by-side overlap, and multiple bonds contain one or more π bonds (in addition to a σ bond).

    PROBLEM \(\PageIndex{2}\)

    How many σ and π bonds are present in the molecule HCN?

    Answer

    \(\ce{H–C≡N}\) has two σ (H–C and C–N) and two π (making the CN triple bond).

    A Lewis structure depicts a hydrogen atom singly bonded to a carbon atom which is triple bonded to a nitrogen atom. The nitrogen atom also has a lone pair of electrons.

    PROBLEM \(\PageIndex{3}\)

    A friend tells you N2 has three π bonds due to overlap of the three p-orbitals on each N atom. Do you agree?

    Answer

    No, two of the p orbitals (one on each N) will be oriented end-to-end and will form a σ bond.

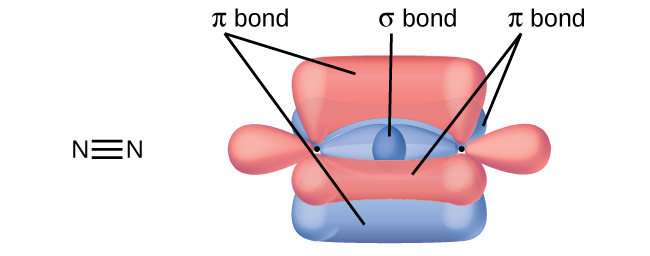
    <div data-mt-source="1"><img alt="" style="width: 650px; height: 256px;" data-cke-saved-src="http://chemwiki.ucdavis.eduhttps://chem.libretexts.org/@api/deki/files/56405/CNX_Chem_08_01_N2LewStru_img.jpg" src="http://chemwiki.ucdavis.eduhttps://chem.libretexts.org/@api/deki/files/56405/CNX_Chem_08_01_N2LewStru_img.jpg"></div>

    PROBLEM \(\PageIndex{4}\)

    Draw the Lewis structures for CO2 and CO, and predict the number of σ and π bonds for each molecule.
    a. CO2
    b. CO

    Answer a

    2 σ 2 π

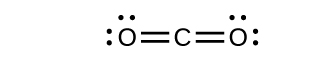
    A Lewis structure shows an oxygen atom double bonded to a carbon atom, which is double bonded to another oxygen atom. Each oxygen atom also has two lone pairs of electrons.

    Answer b

    1 σ 2 π

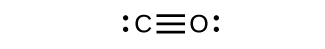
    A Lewis structure shows a carbon atom triple bonded to an oxygen atom. Each atom also has a lone pairs of electrons.

    PROBLEM \(\PageIndex{5}\)

    Why is the concept of hybridization required in valence bond theory?

    Answer

    Hybridization is introduced to explain the geometry of bonding orbitals in valance bond theory.

    PROBLEM \(\PageIndex{6}\)

    Give the shape that describes each hybrid orbital set:

    (a) sp2

    (b) sp

    Answer a

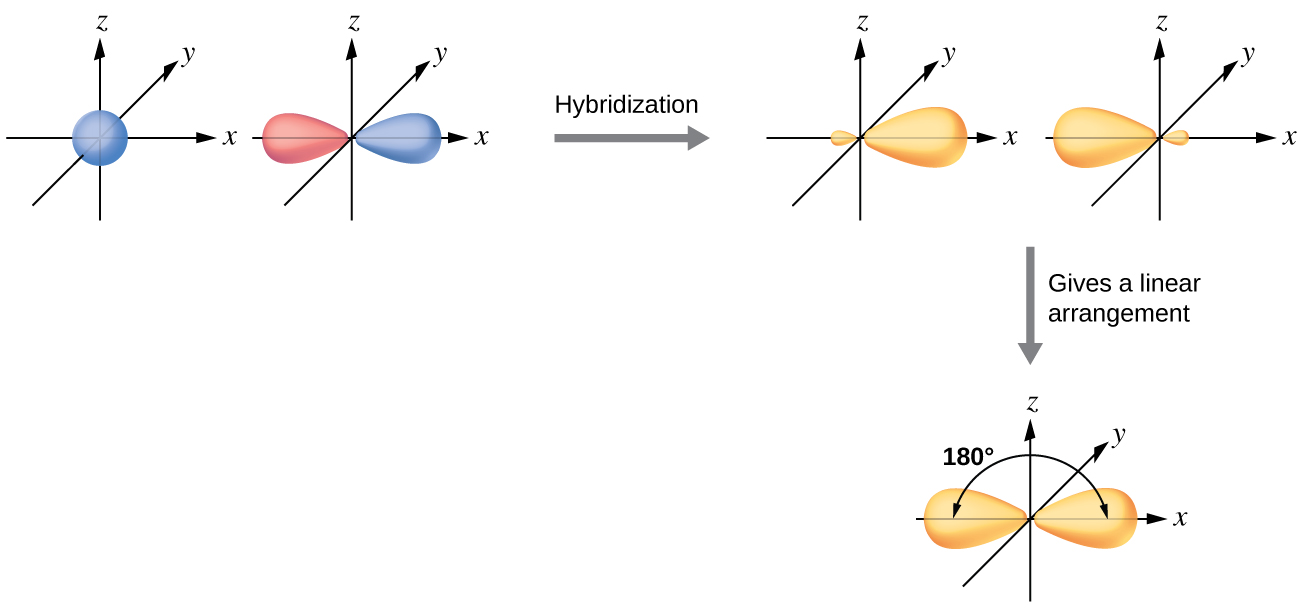
    A series of three diagrams connected by a right-facing arrow that is labeled, “Hybridization,” and a downward-facing arrow labeled, “Gives a linear arrangement,” are shown. The first diagram shows a blue spherical orbital and a red, peanut-shaped orbital, each placed on an X, Y, Z axis system. The second diagram shows the same two orbitals, but they are now purple and have one enlarged lobe and one smaller lobe. Each lies along the x-axis in the drawing. The third diagram shows the same two orbitals, but their smaller lobes now overlap along the x-axis while their larger lobes are located at and labeled as “180 degrees” from one another.

    Answer b

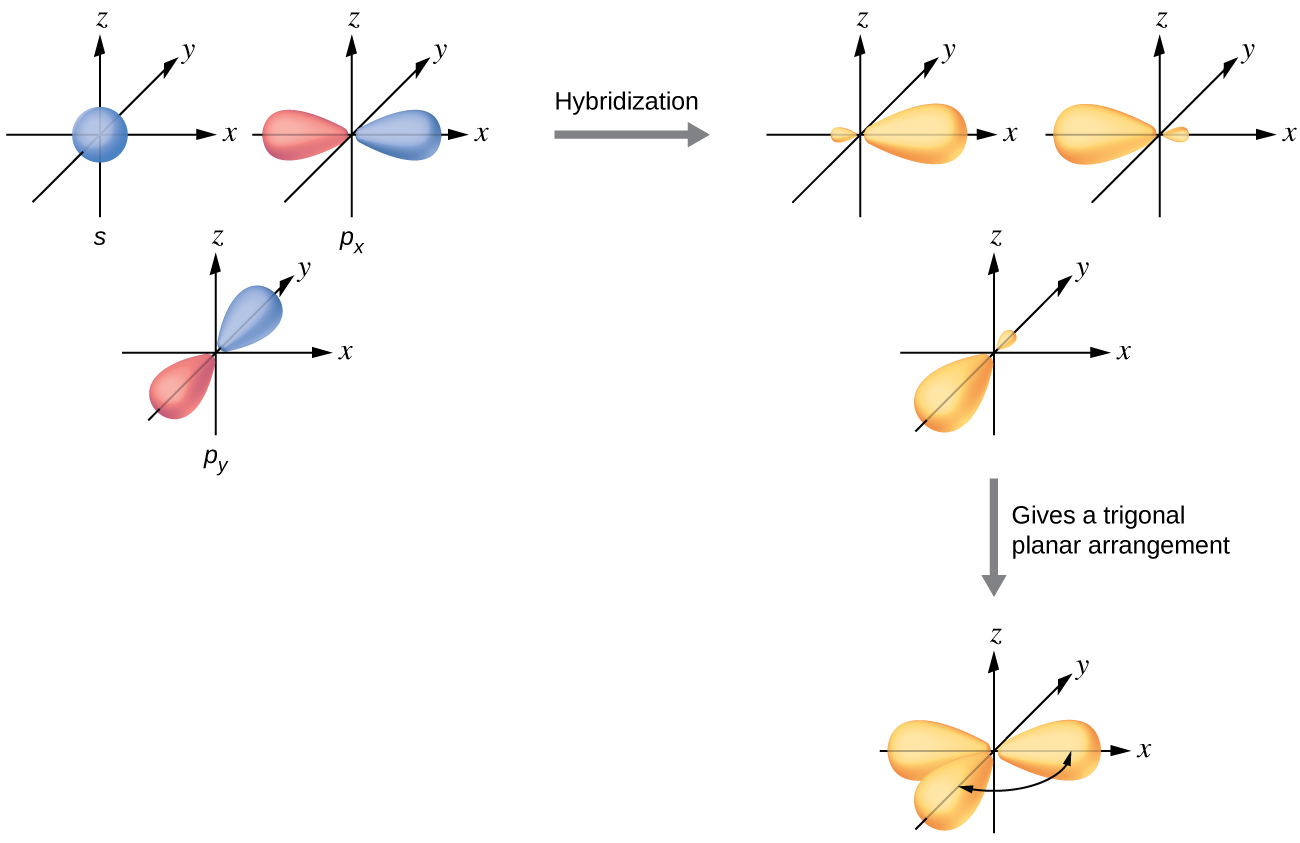
    A series of three diagrams connected by a right-facing arrow that is labeled, “Hybridization,” and a downward-facing arrow labeled, “Gives a trigonal planar arrangement,” are shown. The first diagram shows a blue spherical orbital and two red, peanut-shaped orbitals, each placed on an X, Y, Z axis system. The two red orbitals are located on the x and z axes, respectively. The second diagram shows the same three orbitals, but they are now purple and have one enlarged lobe and one smaller lobe. Each lies in a different axis in the drawing. The third diagram shows the same three orbitals, but their smaller lobes now overlap while their larger lobes are located at and labeled as “120 degrees” from one another.

    PROBLEM \(\PageIndex{7}\)

    What is the hybridization of the central atom in each of the following?

    (a) BeH2

    (b) \(\ce{PO4^3-}\)

    Answer a

    linear

    Answer b

    tetrahedral

    PROBLEM \(\PageIndex{8}\)

    A molecule with the formula AB3 could have one of two different shapes. Give the shape and the hybridization of the central A atom for each.

    Answer

    trigonal planar, sp2; trigonal pyramidal (one lone pair on A) sp3

    PROBLEM \(\PageIndex{9}\)

    Methionine, CH3SCH2CH2CH(NH2)CO2H, is an amino acid found in proteins. Based on the Lewis structure of this compound, what is the hybridization type of each carbon, oxygen, the nitrogen, and the sulfur?

    A Lewis structure is shown in which a carbon atom is single bonded to three hydrogen atoms and single bonded to a sulfur atom with two lone pairs of electrons. The sulfur atom is attached to a chain of four singly bonded carbon atoms, the first two of which are single bonded to two hydrogen atoms each, and the third of which is single bonded to a hydrogen atom and single bonded to a nitrogen atom which has one lone electron pair. The nitrogen atom is also single bonded to two hydrogen atoms. The fourth andfinal carbon in the chain is double bonded to an oxygen with two lone pairs of electrons and single bonded to an oxygen atom with two lone pairs of electrons. The second oxygen atom is single bonded to a hydrogen atom.

    Answer

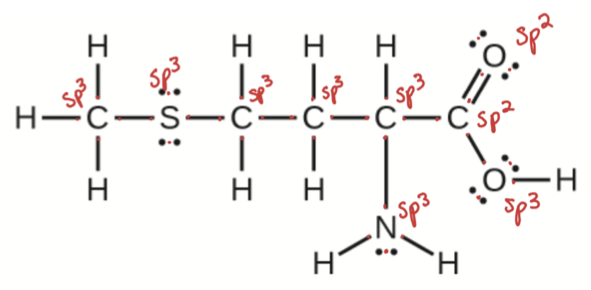
    clipboard_e788ad5fa44ba8b0fede3fa9bad3353ff.png

    Click here to see a video of the solution

    PROBLEM \(\PageIndex{10}\)

    Two important industrial chemicals, ethene, C2H4, and propene, C3H6, are produced by the steam (or thermal) cracking process:

    \(\ce{2C3H8}(g)⟶\ce{C2H4}(g)+\ce{C3H6}(g)+\ce{CH4}(g)+\ce{H2}(g)\)

    For each of the four carbon compounds, do the following:

    (a) Draw a Lewis structure.

    (b) Predict the geometry about the carbon atom.

    (c) Determine the hybridization of each type of carbon atom.

    Answer a

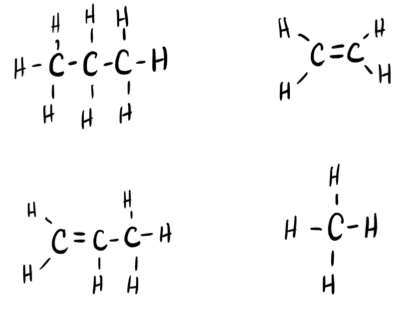
    clipboard_e68de3c41d1cc51ce33ff63e826a59577.png

    Answer b

    C3H8: tetrahedral

    C2H4: trigonal planar

    C3H6: trigonal planar (1&2) and tetrahedral (3)

    CH4: tetrahedral

    Answer c

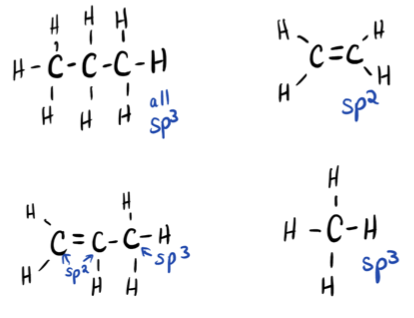
    clipboard_e47ff06f105423808bbd6e868fd63502c.png

    Click here to see a video of the solution

    PROBLEM \(\PageIndex{11}\)

    Consider nitrous acid, HNO2 (HONO).

    (a) Write a Lewis structure.

    (b) What are the electron pair and molecular geometries of the internal oxygen and nitrogen atoms in the HNO2 molecule?

    (c) What is the hybridization on the internal oxygen and nitrogen atoms in HNO2?

    Answer a

    clipboard_e54a70cfabffec02e6270eb37166dbcba.png

    Answer b

    Electron pair: O: tetrahedral, N: trigonal planar

    Molecular geometry: O: bent (109), N: trigonal planar

    Answer c

    O: sp3

    N: sp2

    Click here to see a video of the solution

    PROBLEM \(\PageIndex{12}\)

    Identify the hybridization of each carbon atom in the following molecule. (The arrangement of atoms is given; you need to determine how many bonds connect each pair of atoms.)

    A Lewis structure is shown that is missing all of its bonds. Six carbon atoms form a chain. There are three hydrogen atoms located around the first carbon, two located around the second, one located near the fifth, and two located around the sixth carbon.

    Answer

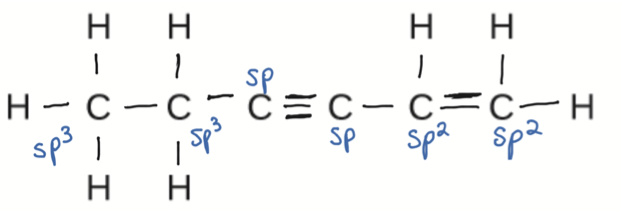
    clipboard_e441749cccd4fc51cc14598bdb4df762a.png

    Click here to see a video of the solution

    Have a video solution request?

    Let your professors know here.

    ***Please know that you are helping future students - videos will be made in time for next term's class.

    Contributors and Attributions

    Feedback

    Think one of the answers above is wrong? Let us know here.

    3.4.2.0: Valence Bond Theory and Hybrid Orbitals (Problems) is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
    2. Tags
      1. source[1]-chem-126656