3.4.0: Bond Strength
- Page ID
- 210709
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Describe the energetics of covalent and ionic bond formation and breakage
A bond’s strength describes how strongly each atom is joined to another atom, and therefore how much energy is required to break the bond between the two atoms. In this section, you will learn about the bond strength of covalent bonds, and then compare that to the strength of ionic bonds, which is related to the lattice energy of a compound.
Bond Strength: Covalent Bonds
Stable molecules exist because covalent bonds hold the atoms together. We measure the strength of a covalent bond by the energy required to break it, that is, the energy necessary to separate the bonded atoms. Separating any pair of bonded atoms requires energy; the stronger a bond, the greater the energy required to break it. The energy required to break a specific covalent bond in one mole of gaseous molecules is called the bond energy or the bond dissociation energy. The bond energy for a diatomic molecule, \(D_{X–Y}\), is defined as the standard enthalpy change for the endothermic reaction:
\[XY_{(g)}⟶X_{(g)}+Y_{(g)}\;\;\; D_{X−Y}=ΔH° \label{7.6.1}\]
For example, the bond energy of the pure covalent H–H bond, \(\Delta_{H–H}\), is 436 kJ per mole of H–H bonds broken:
\[H_{2(g)}⟶2H_{(g)} \;\;\; D_{H−H}=ΔH°=436kJ \label{EQ2}\]
Breaking a bond always require energy to be added to the molecule. Correspondingly, making a bond always releases energy.
Molecules with three or more atoms have two or more bonds. The sum of all bond energies in such a molecule is equal to the standard enthalpy change for the endothermic reaction that breaks all the bonds in the molecule. For example, the sum of the four C–H bond energies in CH4, 1660 kJ, is equal to the standard enthalpy change of the reaction:
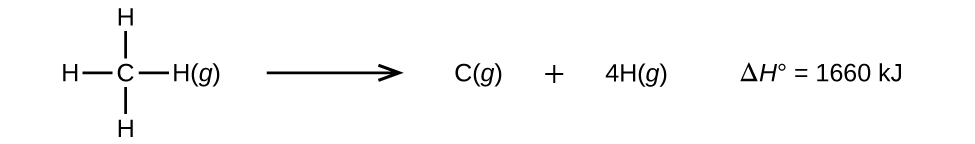
The average C–H bond energy, \(D_{C–H}\), is 1660/4 = 415 kJ/mol because there are four moles of C–H bonds broken per mole of the reaction. Although the four C–H bonds are equivalent in the original molecule, they do not each require the same energy to break; once the first bond is broken (which requires 439 kJ/mol), the remaining bonds are easier to break. The 415 kJ/mol value is the average, not the exact value required to break any one bond.
The strength of a bond between two atoms increases as the number of electron pairs in the bond increases. Generally, as the bond strength increases, the bond length decreases. Thus, we find that triple bonds are stronger and shorter than double bonds between the same two atoms; likewise, double bonds are stronger and shorter than single bonds between the same two atoms. Average bond energies for some common bonds appear in Table \(\PageIndex{2}\), and a comparison of bond lengths and bond strengths for some common bonds appears in Table \(\PageIndex{2}\). When one atom bonds to various atoms in a group, the bond strength typically decreases as we move down the group. For example, C–F is 439 kJ/mol, C–Cl is 330 kJ/mol, and C–Br is 275 kJ/mol.
| Bond | Bond Energy | Bond | Bond Energy | Bond | Bond Energy | ||
|---|---|---|---|---|---|---|---|
| H–H | 436 | C–S | 260 | F–Cl | 255 | ||
| H–C | 415 | C–Cl | 330 | F–Br | 235 | ||
| H–N | 390 | C–Br | 275 | Si–Si | 230 | ||
| H–O | 464 | C–I | 240 | Si–P | 215 | ||
| H–F | 569 | N–N | 160 | Si–S | 225 | ||
| H–Si | 395 | \(\mathrm{N=N}\) | 418 | Si–Cl | 359 | ||
| H–P | 320 | \(\mathrm{N≡N}\) | 946 | Si–Br | 290 | ||
| H–S | 340 | N–O | 200 | Si–I | 215 | ||
| H–Cl | 432 | N–F | 270 | P–P | 215 | ||
| H–Br | 370 | N–P | 210 | P–S | 230 | ||
| H–I | 295 | N–Cl | 200 | P–Cl | 330 | ||
| C–C | 345 | N–Br | 245 | P–Br | 270 | ||
| \(\mathrm{C=C}\) | 611 | O–O | 140 | P–I | 215 | ||
| \(\mathrm{C≡C}\) | 837 | \(\mathrm{O=O}\) | 498 | S–S | 215 | ||
| C–N | 290 | O–F | 160 | S–Cl | 250 | ||
| \(\mathrm{C=N}\) | 615 | O–Si | 370 | S–Br | 215 | ||
| \(\mathrm{C≡N}\) | 891 | O–P | 350 | Cl–Cl | 243 | ||
| C–O | 350 | O–Cl | 205 | Cl–Br | 220 | ||
| \(\mathrm{C=O}\) | 741 | O–I | 200 | Cl–I | 210 | ||
| \(\mathrm{C≡O}\) | 1080 | F–F | 160 | Br–Br | 190 | ||
| C–F | 439 | F–Si | 540 | Br–I | 180 | ||
| C–Si | 360 | F–P | 489 | I–I | 150 | ||
| C–P | 265 | F–S | 285 |
| Bond | Bond Length (Å) | Bond Energy (kJ/mol) |
|---|---|---|
| C–C | 1.54 | 345 |
| \(\mathrm{C=C}\) | 1.34 | 611 |
| \(\mathrm{C≡C}\) | 1.20 | 837 |
| C–N | 1.43 | 290 |
| \(\mathrm{C=N}\) | 1.38 | 615 |
| \(\mathrm{C≡N}\) | 1.16 | 891 |
| C–O | 1.43 | 350 |
| \(\mathrm{C=O}\) | 1.23 | 741 |
| \(\mathrm{C≡O}\) | 1.13 | 1080 |
We can use bond energies to calculate approximate enthalpy changes for reactions where enthalpies of formation are not available. Calculations of this type will also tell us whether a reaction is exothermic or endothermic.
- An exothermic reaction (ΔH negative, heat produced) results when the bonds in the products are stronger than the bonds in the reactants.
- An endothermic reaction (ΔH positive, heat absorbed) results when the bonds in the products are weaker than those in the reactants.
The enthalpy change, ΔH, for a chemical reaction is approximately equal to the sum of the energy required to break all bonds in the reactants (energy “in”, positive sign) plus the energy released when all bonds are formed in the products (energy “out,” negative sign). This can be expressed mathematically in the following way:
\[\Delta H=\sum D_{\text{bonds broken}}− \sum D_{\text{bonds formed}} \label{EQ3}\]
In this expression, the symbol \(\Sigma\) means “the sum of” and D represents the bond energy in kilojoules per mole, which is always a positive number. The bond energy is obtained from a table and will depend on whether the particular bond is a single, double, or triple bond. Thus, in calculating enthalpies in this manner, it is important that we consider the bonding in all reactants and products. Because D values are typically averages for one type of bond in many different molecules, this calculation provides a rough estimate, not an exact value, for the enthalpy of reaction.
Consider the following reaction:
or
\[\ce{H–H_{(g)} + Cl–Cl_{(g)}⟶2H–Cl_{(g)}} \label{\EQ5}\]
To form two moles of HCl, one mole of H–H bonds and one mole of Cl–Cl bonds must be broken. The energy required to break these bonds is the sum of the bond energy of the H–H bond (436 kJ/mol) and the Cl–Cl bond (243 kJ/mol). During the reaction, two moles of H–Cl bonds are formed (bond energy = 432 kJ/mol), releasing 2 × 432 kJ; or 864 kJ. Because the bonds in the products are stronger than those in the reactants, the reaction releases more energy than it consumes:
\[\begin {align*}
ΔH&= \sum \mathrm{D_{bonds\: broken}}− \sum \mathrm{D_{bonds\: formed}}\\
ΔH&=\mathrm{[D_{H−H}+D_{Cl−Cl}]−2D_{H−Cl}}\\
&=\mathrm{[436+243]−2(432)=−185\:kJ}
\end {align*}\]
This excess energy is released as heat, so the reaction is exothermic. Table T2 gives a value for the standard molar enthalpy of formation of HCl(g), \(ΔH^\circ_\ce f\), of –92.307 kJ/mol. Twice that value is –184.6 kJ, which agrees well with the answer obtained earlier for the formation of two moles of HCl.
Example \(\PageIndex{1}\): Using Bond Energies to Approximate Enthalpy Changes
Methanol, CH3OH, may be an excellent alternative fuel. The high-temperature reaction of steam and carbon produces a mixture of the gases carbon monoxide, CO, and hydrogen, H2, from which methanol can be produced. Using the bond energies in Table \(\PageIndex{2}\), calculate the approximate enthalpy change, ΔH, for the reaction here:
\[CO_{(g)}+2H2_{(g)}⟶CH_3OH_{(g)}\]
Solution
First, we need to write the Lewis structures of the reactants and the products:
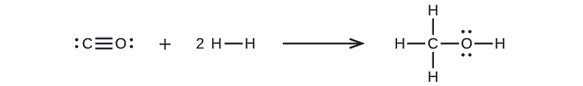
From this, we see that ΔH for this reaction involves the energy required to break a C–O triple bond and two H–H single bonds, as well as the energy produced by the formation of three C–H single bonds, a C–O single bond, and an O–H single bond. We can express this as follows (via Equation \ref{EQ3}):
\[\begin {align*}
ΔH&= \sum D_{bonds\: broken}− \sum D_{bonds\: formed}\\
ΔH&=\mathrm{[D_{C≡O}+2(D_{H−H})]−[3(D_{C−H})+D_{C−O}+D_{O−H}]}
\end {align*}\]
Using the bond energy values in Table \(\PageIndex{2}\), we obtain:
ΔH&=[1080+2(436)]−[3(415)+350+464]\\
&=\ce{−107\:kJ}
\end {align*}\]
We can compare this value to the value calculated based on \(ΔH^\circ_\ce f\) data from Appendix G:
ΔH&=[ΔH^\circ_{\ce f}\ce{CH3OH}(g)]−[ΔH^\circ_{\ce f}\ce{CO}(g)+2×ΔH^\circ_{\ce f}\ce{H2}]\\
&=[−201.0]−[−110.52+2×0]\\
&=\mathrm{−90.5\:kJ}
\end {align*}\]
Note that there is a fairly significant gap between the values calculated using the two different methods. This occurs because D values are the average of different bond strengths; therefore, they often give only rough agreement with other data.
Exercise \(\PageIndex{1}\)
Ethyl alcohol, CH3CH2OH, was one of the first organic chemicals deliberately synthesized by humans. It has many uses in industry, and it is the alcohol contained in alcoholic beverages. It can be obtained by the fermentation of sugar or synthesized by the hydration of ethylene in the following reaction:

Using the bond energies in Table \(\PageIndex{2}\), calculate an approximate enthalpy change, ΔH, for this reaction.
- Answer
-
–35 kJ
Summary
The strength of a covalent bond is measured by its bond dissociation energy, that is, the amount of energy required to break that particular bond in a mole of molecules. Multiple bonds are stronger than single bonds between the same atoms. The enthalpy of a reaction can be estimated based on the energy input required to break bonds and the energy released when new bonds are formed. Key Equations
- Bond energy for a diatomic molecule: \(\ce{XY}(g)⟶\ce{X}(g)+\ce{Y}(g)\hspace{20px}\ce{D_{X–Y}}=ΔH°\)
- Enthalpy change: ΔH = ƩDbonds broken – ƩDbonds formed
Footnotes
- This question is taken from the Chemistry Advanced Placement Examination and is used with the permission of the Educational Testing Service.
Glossary
- bond energy
- (also, bond dissociation energy) energy required to break a covalent bond in a gaseous substance
Contributors and Attributions
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).
- Adelaide Clark, Oregon Institute of Technology

