Section 3.2: Point Groups

Introduction

In group theory, molecules or other objects can be organized into point groups based on the type and number of symmetry operations they possess. Every molecule in a point group will have all of the same symmetry operations as any other molecule in that same point group. The most common, and chemically relevant point groups are described below.

The Low Symmetry Point Groups

C₁ Point Group

Overall, we divide point groups into three major categories: High symmetry point groups, low symmetry point groups, dihedral point groups, and rotational point groups. Let us begin with the low symmetry point groups. As the name says, these point groups only have few symmetry elements and operations. The point group C₁ is the point group with the lowest symmetry. Molecules that belong to this point group only have the identity as symmetry element.

Figure \(\PageIndex{1}\) C₁ point group of bromochlorofluromethane (Attribution: symotter.org/gallery)

An example is the bromochlorofluromethane molecule (Figure \(\PageIndex{1}\)). It has no symmetry element except the identity (E). The name C₁ comes from the symmetry element C₁. A C₁ operation is the same as the identity.

C_s Point Group

The point group C_s has a mirror plane in a addition to the identity. An example is the 1,2-bromochloroethene molecule (Figure \(\PageIndex{2}\)).

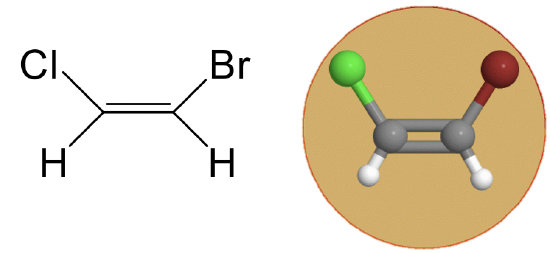Figure \(\PageIndex{2}\) C_s point group of 1,2-bromochloroethene (Attribution: symotter.org/gallery)

This is a planar molecule and the mirror plane is within the plane of the molecule. This mirror plane does not move any atoms when the reflection operation is carried out, nonetheless it exists because any point of the molecule above the mirror plane will be found below the mirror plane after the execution of the operation. Vice versa, any point below the mirror plane will be above the mirror plane. This mirror plane does not have a vertical or horizontal mirror plane designation because no proper rotational axes exist.

C_i Point Group

The point group C_i has the inversion as the only symmetry element besides the identity. The point group C_i is sometimes also called S₂ because an S₂ improper rotation-reflection is the same as an inversion. An example is the 1,2-dibromo 1,2-dichloro ethane (Figure \(\PageIndex{3}\)).

Figure \(\PageIndex{3}\) The C_i point group: 1,2-dibromo-1,2-dichloroethane (Attribution: symotter.org/gallery)

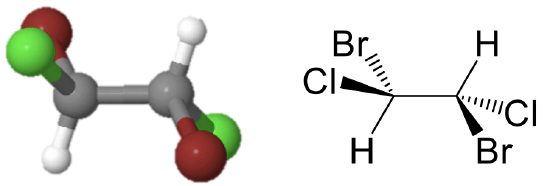
This molecule looks quite symmetric, but it has inversion center in the middle of the carbon-carbon bond as the only symmetry element. Upon execution of the inversion operation, the two carbons swap up their positions, and so do the two bromine, the two chorine, and the two hydrogen atoms.

The High Symmetry Point Groups

The symmetry elements of the high symmetry point groups can be more easily understood when the properties of platonic solids are understood first. Platonic solids are polyhedra made of regular polygons. In a platonic solid all faces, edges, and vertices (corners) are symmetry-equivalent. We will see that this is a property that can be used to understand the symmetry elements in high symmetry point groups. There are only five possibilities to make platonic solids from regular polygons (Figure \(\PageIndex{4}\)).

Figure \(\PageIndex{4}\) The platonic solids (Attribution: Drummyfish [CC0] https://commons.wikimedia.org/wiki/F...ransparent.svg)

The first possibility is to construct a tetrahedron from four regular triangles. The second platonic solid is the octahedron made of eight regular triangles. The third possibility is the icosahedron made of twenty triangles. In addition, six squares can be connected to form a cube, and twelve pentagons can be connected to form a dodecahedron. There are no possibilities to connect other regular polygons like hexagons to make a platonic solid.

The T_d Point Group

The tetrahedron, as well as tetrahedral molecules and anions such as CH₄ and BF₄- belong to the high symmetry point group T_d (Note that only tetrahedral molecules where all four outer atoms/groups are the same will be in the T_d point group). Let us find the symmetry elements and symmetry operations that belong to the point group T_d. First, we should not forget the identity operation, E. Next, it is useful to look for the principal axes.

Figure \(\PageIndex{5}\) The C₃ axes in a tetrahedron (Attribution: symotter.org/gallery)

The tetrahedron has four principal C₃ axes (Figure \(\PageIndex{5}\)). It is a property of the high-symmetry point groups that they have more than one principal axis. The C₃ axes go through the vertices of the tetrahedron. Because each C₃ axis goes through one vertex, there are four vertices, and we know that in a platonic solid all vertices are symmetry-equivalent, we can understand that there are four C₃ axes. How many unique C₃ operations are associated with these axes? After three rotations around 120° we reach the identity. Therefore C₃³=E, and we only need to consider the C₃¹ and the C₃² rotation about 120 and 240° respectively. Because there are four C₃ axes, there are four C₃¹ and four C₃² operations and eight C₃ operations overall. In addition to the C₃ axes there are C₂ axes (Figure \(\PageIndex{6}\)).

Figure \(\PageIndex{6}\) The C₂ axes in a tetrahedron belonging to the point group T_d (Attribution: symotter.org/gallery)

You can see that a C₂ axis goes through two opposite edges in the tetrahedron. Because a tetrahedron has six edges, and each C₂ axis go through two edges there are 6/2=3 C₂ axes. There is only one C₂ symmetry operation per C₂ axis because we produce the identity already after two rotations. Therefore there are three C₂¹ operations overall.

Figure \(\PageIndex{7}\) The S₄ axes in a tetrahedron (Attribution: symotter.org/gallery)

In addition, the T_d point group has S₄ improper rotation reflections. Like the C₂ axes, they pass through the middle of two opposite edges. This also means that they are superimposing the C₂ axes. Because there are six edges, and two S₄ axes per edge there are 6/2=3 S₄ axes (Figure \(\PageIndex{7}\)). How many operations are associated with these S₄ axes? The order of the axes are even, and therefore we need four S₄ operations to produce the identity. The S₄² operation is the same as a C₂¹ operation because reflecting two times is equivalent to not reflecting at all, and rotating two times by 90° is the same as rotating about 180°. Therefore overall, only S₄¹ and S₄³ operations are unique operations. S₄² and S₄⁴ can be expressed by the simpler operations C₂¹ and E respectively. Because there are 3 S₄ axes, there are three S₄¹ and three S₄³ operations. Overall there are six S₄ operations.

Figure \(\PageIndex{8}\) The mirror planes and C₂ axes in a tetrahedron belonging to the point group T_d (Attribution: symotter.org/gallery)

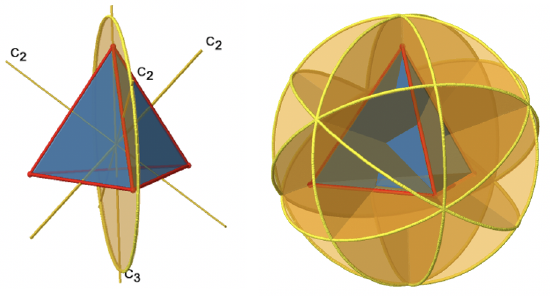
There are also mirror planes (Figure \(\PageIndex{8}\)). The planes contain a single edge of the tetrahedron, thereby bisecting the tetrahedron. There a six edges in a tetrahedron, and therefore there are 6/1=6 mirror planes.These planes are dihedral planes because each plane contains a C₃ principal axis and is bisects the angle between two C₂ axes. Overall, there are three C₂ axes and three C₂ operations. There is one reflection operation per mirror plane because reflecting two times produces the identity. Therefore, there are six σ_d reflection operations.

Symmetry Operations in the T_d Point Group

Every molecule or object in the T_d point group has the following symmetry operations:

• E, 8 C₃, 3 C₂, 6 S₄, and 6 σ_d

The Octahedral Point Group O_h

Another high symmetry point group is the point group O_h. Both the octahedron as well as the cube belong to this point group despite their very different shape Figure \(\PageIndex{9}\). Because they belong to the same point group they must have the same symmetry elements and operations. There are many octahedrally shaped molecules, such as the SF₆.

Figure \(\PageIndex{9}\): SF₆ and cubane with cubic and octahedral shape, respectively, belong to the point group O_h (Attribution: symotter.org/gallery)

Molecules with cubic shapes are far less common, because a cubic shape often leads to significant strain in the molecule. An example is cubane C₈H₈. Let us determine the symmetry elements and operations for the point group O_h using the example of the octahedron. If we used the cube, we would get exactly the same results.

There are three C₄ principal axes in the octahedron. They go through two opposite vertices of the octahedron (Figure \(\PageIndex{10}\)). There are three C₄ axes because an octahedron has six vertices which are all symmetry-equivalent because the octahedron is a platonic solid.

Figure \(\PageIndex{10}\): The C₄ and C₂ axes in the octahedral point group O_h (Attribution: symotter.org/gallery)

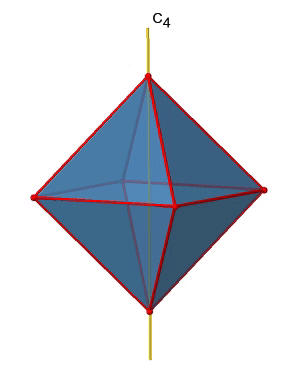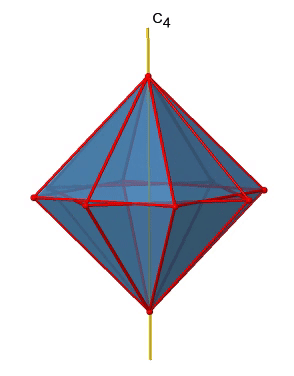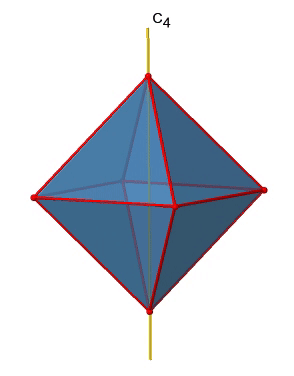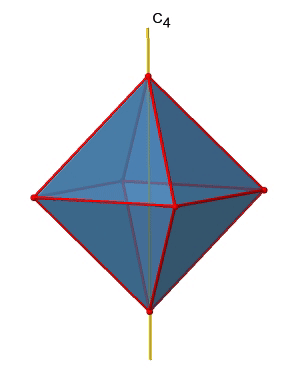
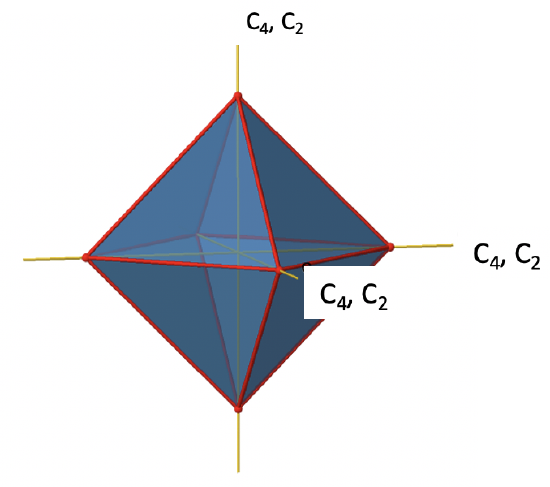
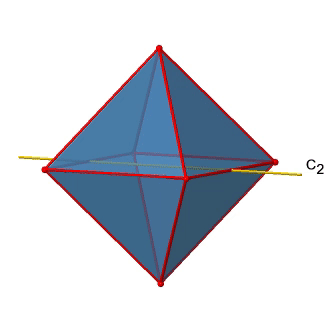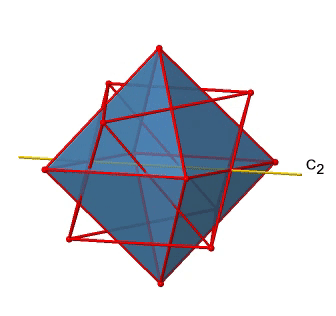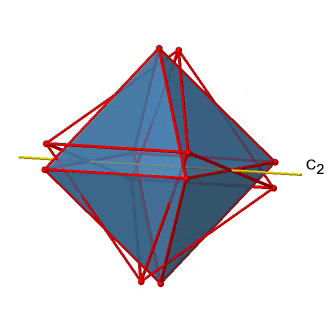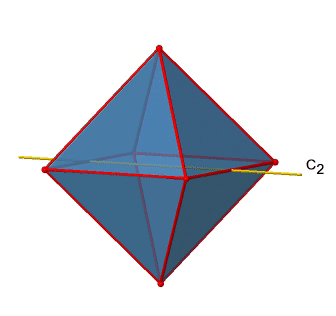
We can see that there are also C₂ axes where the C₄ axes run. This is because rotating two times around 90° is the same as rotating around 180°. What are the symmetry operations associated with these symmetry elements? Rotating four times around 90° using the C₄ axes produces the identity. So we have to consider the operations C₄¹, C₄², C₄³ and C₄⁴. How many of these are unique? C₄⁴ is the same as the identity, so it is not unique, In addition a C₄² is identical to a C₂¹, and thus C₄² is also not unique, and can be expressed by the simpler operation C₂¹. That leaves the C₄¹ and the C₄³ as the only unique symmetry operations. Because we have three C₄ axes, there are 2x3=6 C₄ operations, in detail there are 3C₄¹ and three C₄³ operations. In addition, there are the three C₂¹ operations belonging the the three C₂ axes.

Figure \(\PageIndex{11}\): The C₃ axes in the octahedral point group O_h (Attribution: symotter.org/gallery)

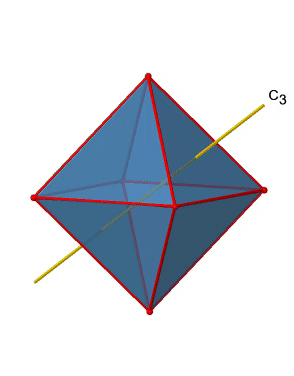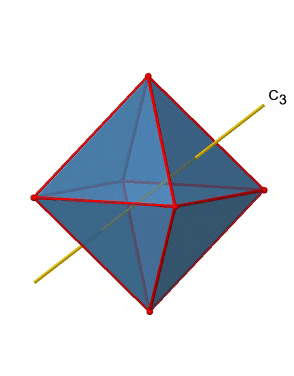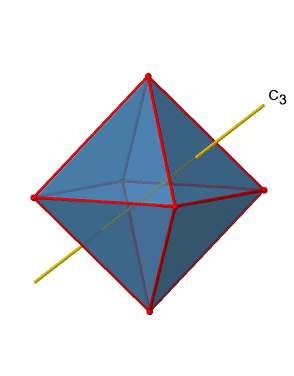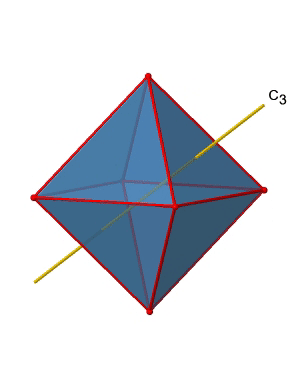
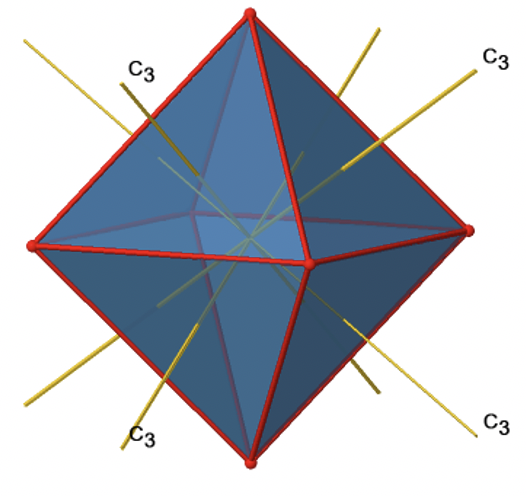
In addition, there are four C₃ axes (Figure \(\PageIndex{11}\):). They are going through the center of two opposite triangular faces of the octahedron.You see above a single C₃ axis, and on the right hand side all four of these axes. How can we understand that there are four axes? An octahedron has overall eight triangular faces, and each C₃ axis goes through two opposite faces, so there are 8/2=4 C₃ axes. Each C₃ axis has the C₃¹ and the C₃² as unique symmetry operations. The C₃³ is the same as the identity. So overall we have 4x2=8 operations, four of them are C₃¹, and four of them are C₃².

Figure \(\PageIndex{12}\): The C₂' axes in the octahedral point group O_h (Attribution: symotter.org/gallery)

In addition to the C₂ axes that superimpose the C₄ axes, there are C₂’ axes which go though two opposite edges of the octahedron (Figure \(\PageIndex{12}\):). How many of them are there? An octahedron has twelve edges, and because each C₂’ passes through two edges, there must be 12/2=6 C₂’ axes. These axes have primes because they are not conjugate to the C₂ axes that superimpose the C₄ axes. For each C₂’ axis there is only the C₂’ ¹ as the unique symmetry operation, and therefore there are overall 6 C₂’¹ symmetry operations.

Figure \(\PageIndex{13}\): The horizontal mirror planes in the octahedral point group O_h (Attribution: symotter.org/gallery)

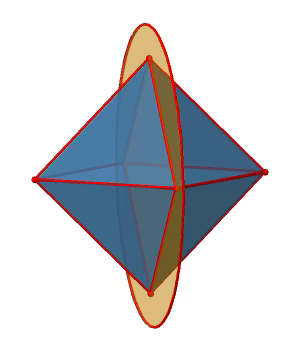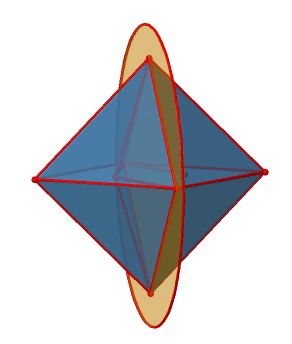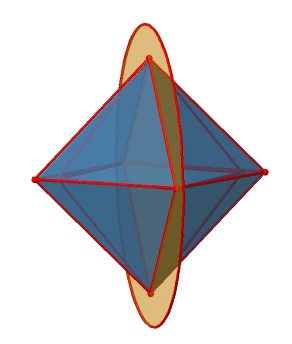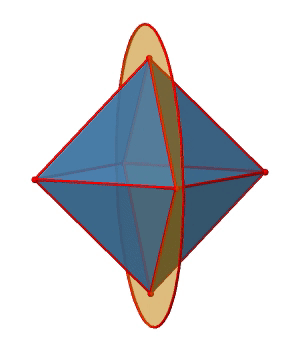
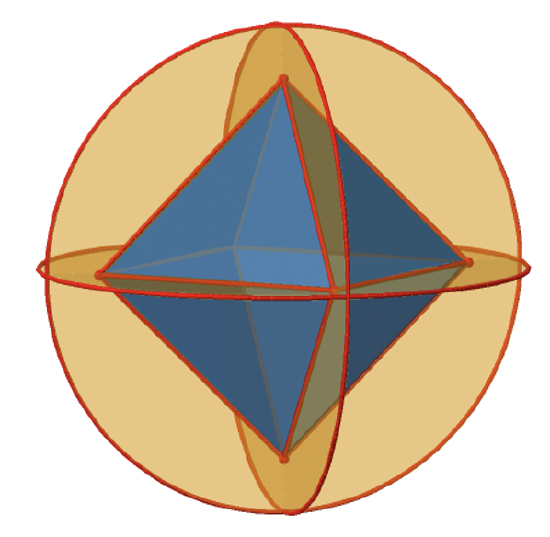
Let us look at the horzontal mirror planes next (Figure \(\PageIndex{13}\)). There are horizontal mirror planes that stand perpendicular to the C₄ principal axes. Note that this mirror plane also contains two axes, in addition to the one to which it stands perpendicular. Because it contains two principal C₄ axes, it has also properties of a vertical mirror plane. Nonetheless, we call it a horizontal mirror plane because it stands perpendicular to the third C₄. The horizontal properties trump the vertical ones, so to say. You can see that a single mirror plane contains four edges of the octahedron. Because there are twelve edges, there are 12/4=3 horizontal mirror planes. There is one mirror plane per principal C₄ axis. There are three horizontal reflection operations because there is always only one reflection operation per mirror plane

Figure \(\PageIndex{14}\): The vertical mirror planes in the octahedral point group O_h (Attribution: symotter.org/gallery)

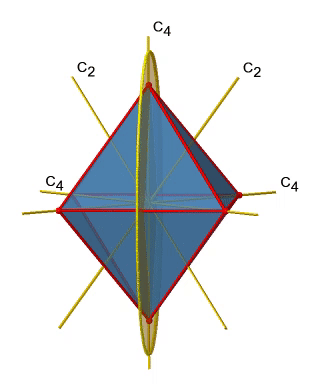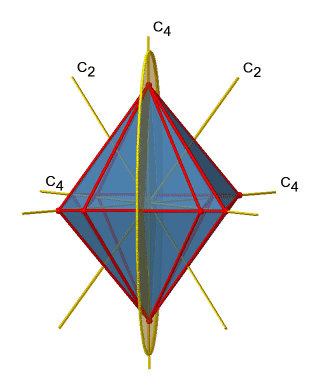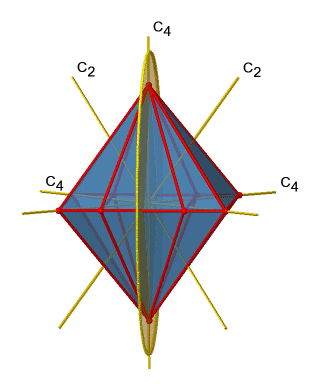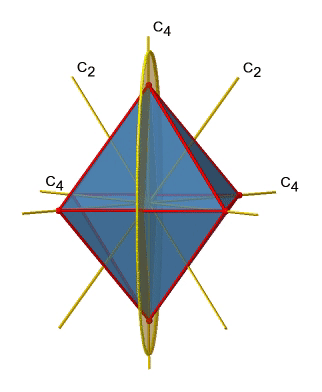
Next let us look for vertical mirror planes (Figure \(\PageIndex{14}\)). You can see that - contrast to the horizontal mirror planes - it does not contain any edges. Rather, it cuts through two opposite edges. You can see that this plane contains a C₄ axis, but it does not stand perpendicular to the other two C₄ axes. Therefore it has only the properties of a vertical mirror plane. You can see however, that the mirror plane bisects the angle between two C₂’ axes which also depicted. This makes the vertical mirror planes dihedral mirror planes, σ_d. How may of them do we have? As previously mentioned, each mirror plane cuts through two opposite edges. There are twelve edges in an octahedron, and thus there are 12/2=6 dihedral mirror planes. You can see all of them on the right side of Figure \(\PageIndex{14}\). Each mirror plane is associated with one reflection operation, therefore there are six dihedral reflection operations.

Next we can ask if the point group O_h has an inversion center? Yes, there is one in the center of the octahedron (Figure \(\PageIndex{15}\))!

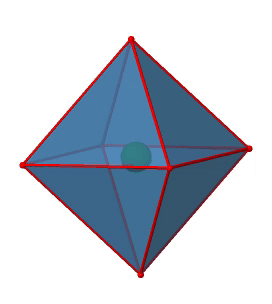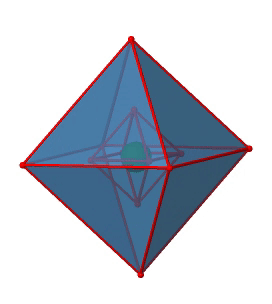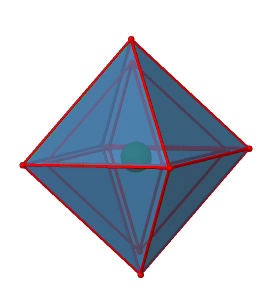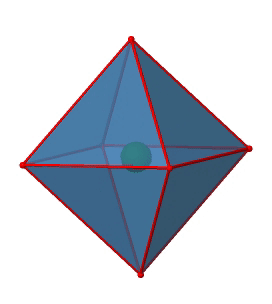
Figure \(\PageIndex{15}\): The inversion center of the octahedral point group O_h (Attribution: symotter.org/gallery)

Each point in the octahedron can be moved through the inversion center to the other side, and the produced octahedron will superimpose the original one. There is always one inversion operation associated with an inversion center.

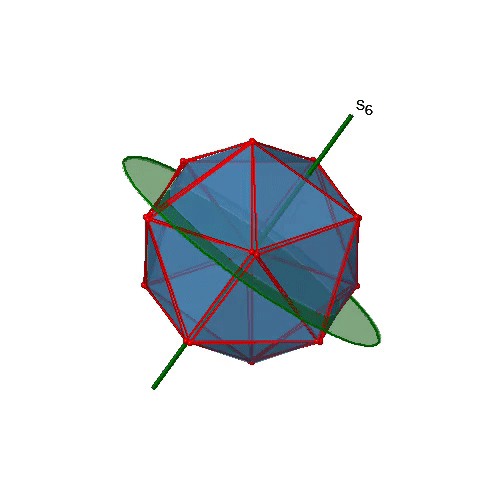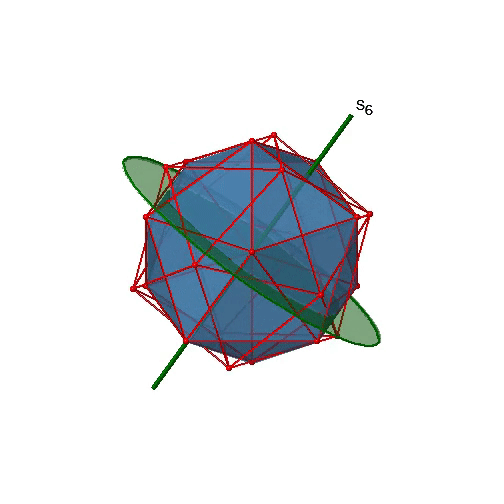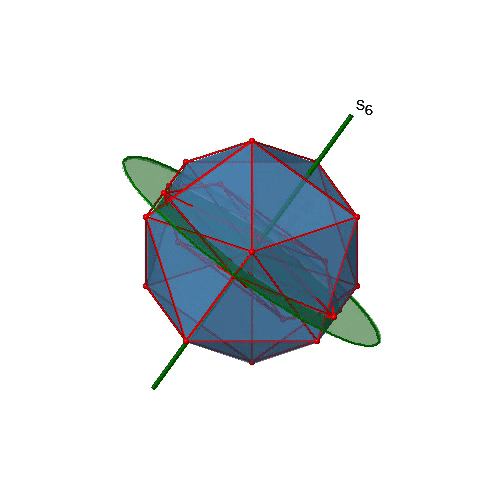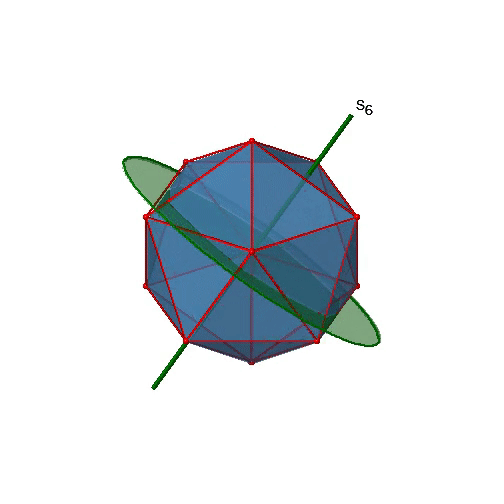
Next, let us look for improper rotations. You can see an S₆ improper rotation operation below (Figure \(\PageIndex{16}\), left).

Figure \(\PageIndex{16}\): The S₆ improper rotation element of the octahedral point group O_h (Attribution: symotter.org/gallery)

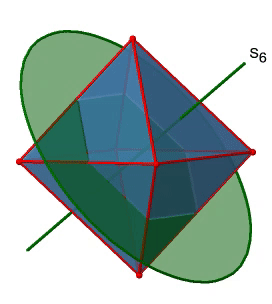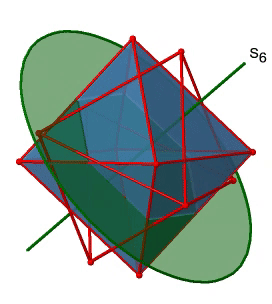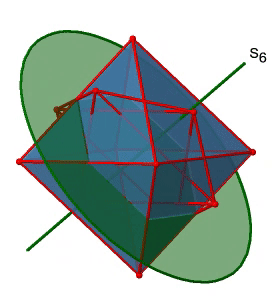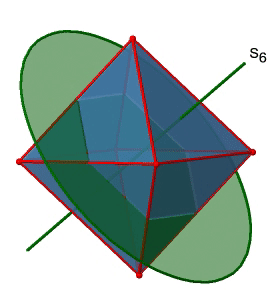
The improper S₆ axis passes though the centers of two opposite triangular faces. One can see that rotation about 60° alone does not make the octahedron superimpose. The reflection at a plane perpendicular to the improper axis is required to achieve superposition. Overall, the rotation-reflection swaps up the position of the two opposite triangular faces. How many S₆ improper axes are there? Since each S₆ passes through two faces, and an octahedron has 8 faces there must be 8/2=4 S₄ axes. You can see all of them above (Fig. 2.2.31, right). Note that they are in the same position as the 4C₃ axes we previously discussed. How many unique operations are associated with them? For an S₆ axis we need to consider operations from S₆¹ to S₆⁶. S₆⁶ is the same as the identity so it is not unique. The S₆² is the same as a C₃¹ because rotating two times round 60° is the same as rotating around 120°, and reflecting twice is the same as not reflecting at all. Similarly, an S₆⁴ is the same as an C₃². Rotating four time by 60° is the same as rotating two times by 120° and reflecting four times is the same as not reflecting at all. Further, an S₆³ is the same as an inversion. After three 60° rotations we have rotated by 180°. If we reflect after that, then this is the same as an S₂¹ operation which is the same as an inversion. Therefore, only the S₆¹ and the S₆⁵ operations are unique, all other operations can be expressed by simpler operations.

Figure \(\PageIndex{17}\): The S₄ improper axis of the octahedral point group O_h (Attribution: symotter.org/gallery)

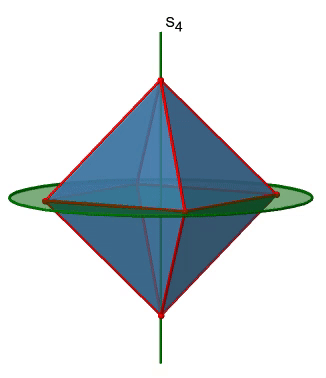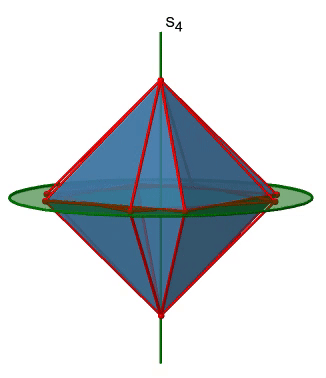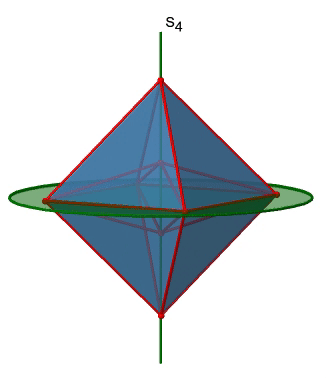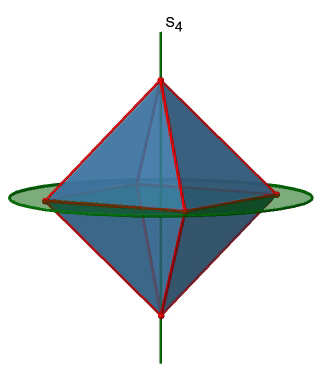
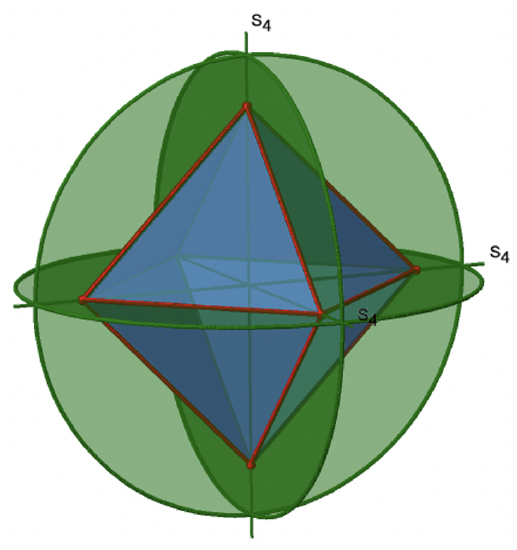
The octahedron also has S₄ improper axes, and you can see one of them in Figure \(\PageIndex{17}\), right). It goes through two opposite corners of the octahedron. The S₄ improper axis seemingly does the same as the C₄ axis that goes through the same two opposite vertices, but actually does not. While rotating around 90° already makes the octahedron superimpose with its original form, executing the reflection operation after the rotation swaps up the position of the two vertices, and generally all points of the octahedron above and below the plane, respectively. Overall the S₄ moves the points within the object differently compared to the C₄ which makes it an additional, unique symmetry element. There are overall three S₄ improper axes because the octahedron has six vertices and one S₄ passes through two vertices.

Symmetry Operations in the O_h Point Group

Every molecule or object in the O_h point group has the following 48 symmetry operations:

• E, 8 C₃, 6 C₂, 6 C₄, 3 C₂ (C₄²), i, 6 S₄, 8 S₆, 3 σ_h, and 6 σ_d

The I_h Point Group

The two remaining platonic solids, the icosahedron and the dodecahedron, belong both to the icosahedral point group I_h. This is despite they are made of different polygons. Because they belong to the same point group, they have exactly the same symmetry operations. An example for a molecule with icosahedral shape is the molecular anion B₁₂H₁₂^2-. Examples of molecules with dodecahedral shape include dodecahedrane (C₂₀H₂₀) and buckminsterfullerene (C₆₀). Let us determine the symmetry elements and symmetry operations for the example of the icosahedron. We could also use the dodecahedron, and the results would be the same. The principal axes of the icosahedron are the C₅ axes. You can see one of them, going through the center of the pentagon comprised of five triangular faces below (Figure \(\PageIndex{18}\)).

 

Figure \(\PageIndex{18}\): One of the C₅ axes of the icosahedron stands perpendicular to the paper plane going through the center of a pentagon of the icosahedron (Attribution: symotter.org/gallery)

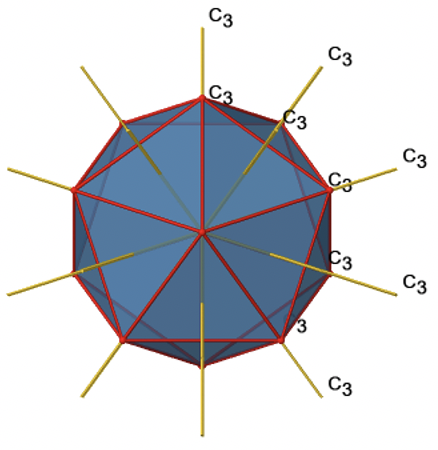
You can understand that there is a C₅ when considering that there are five triangular faces making a pentagon. The C₅ axis sits in the center of the pentagon. We can see that when we rotate around this C₅ axis, then the produced icosahedron superimposes the original one. The C₅ axis goes through two opposite vertices of the icosahedron. Because an icosahedron has 12 vertices, there must be six C₅ axes overall. You can see all of them below (Figure \(\PageIndex{19}\)). There are four unique symmetry operations associated with a single C₅ axis, namely the C₅¹, the C₅², the C₅³, and the C₅⁴. The C₅⁵ is the same as the identity. Because there are six C₅ axes, there are overall 6x4=24 C₅ symmetry operations.

Figure \(\PageIndex{19}\): The C₅ axes of the icosahedron (Attribution: symotter.org/gallery)

Figure \(\PageIndex{20}\): One of the C₃ axes of the icosahedral point group (Attribution: symotter.org/gallery)

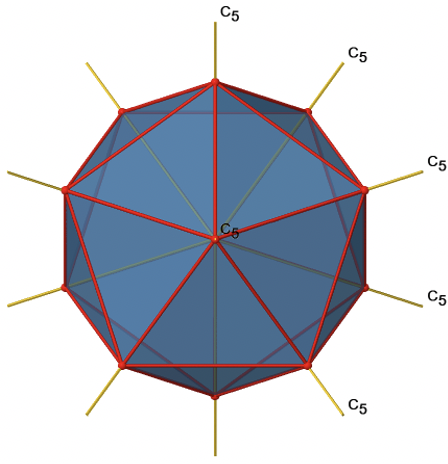
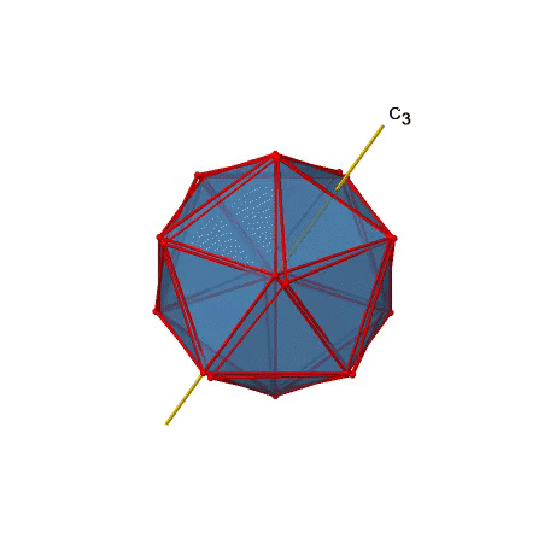
In addition, there are C₃ axes. One of them is shown below, and you can see that it passes through the centers of two opposite triangular faces (Figure \(\PageIndex{20}\)). As one rotates by 120° the atoms on the triangular faces change their position, and the resulting icosahedron superimposes the original one. As the name icosahedron says, there are twenty faces overall.

Figure \(\PageIndex{21}\): The C₃ axes of the icosahedral point group (Attribution: symotter.org/gallery)

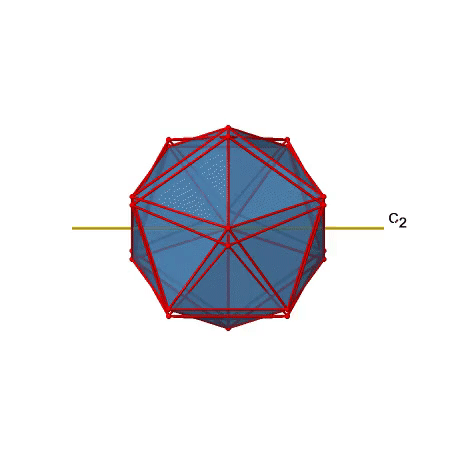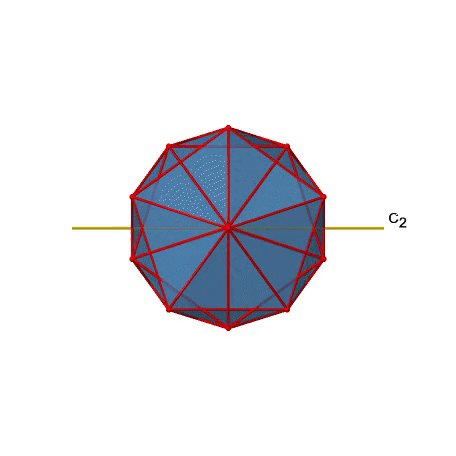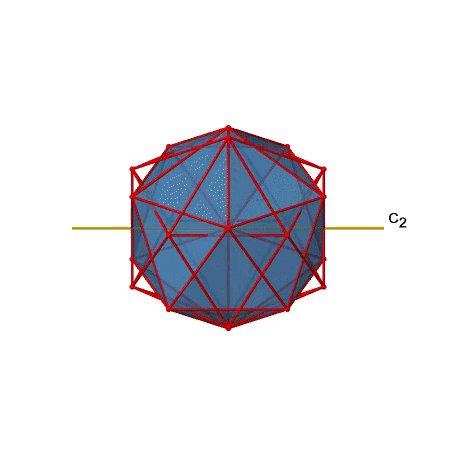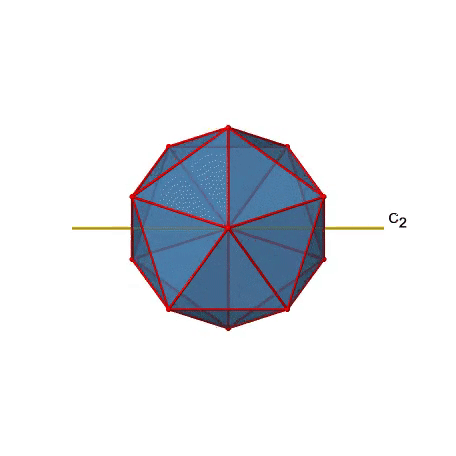
Because one C₃ passes through two opposite axes, there are 20/2=10 C₃ axes overall (Figure \(\PageIndex{21}\):). Each C₃ axis is associated with two symmetry operations, namely C₃¹, and C₃². Thus, there are overall 10x2=20 C₃ symmetry operations.

Figure \(\PageIndex{22}\): The C₂ axes of the icosahedral point group (Attribution: symotter.org/gallery)

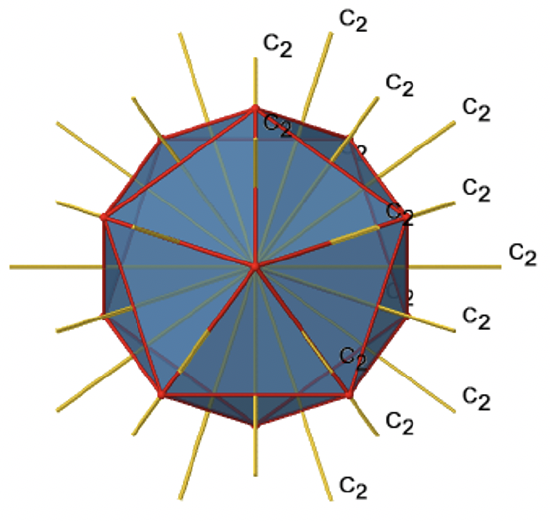
There are also C₂ axes (Figure \(\PageIndex{21}\)). They pass through the centers of two opposite edges of the icosahedron. Rotating around the C₂ axis shown makes the icosahedron superimpose. An icosoahedron has overall 30 edges. Because one C₂ axis passes through the centers of two opposite edges, we can understand that there are 30/2=15 C₂ axes. There is one unique C₂ operation per axis, and therefore there are 15 C₂ operations.

We have now found all proper rotations. Let us look for mirror planes, next. You can see a mirror plane below (Figure \(\PageIndex{22}\)).

 

Figure \(\PageIndex{22}\): A mirror plane in the icosahedral point group (Attribution: symotter.org/gallery)

It contains two opposite edges. It also bisects two other edges. An icosahedron has overall 30 edges, therefore there are 30/2=15 mirror planes. You can see all of them below (Figure \(\PageIndex{23}\))).

Figure \(\PageIndex{23}\): All the mirror planes in the icosahedral point group (Attribution: symotter.org/gallery)

The icosahedron also has an inversion center in the center of the icosahedron (Figure \(\PageIndex{24}\)). As we carry out the associated symmetry operation, all points in the icosahedron move through the inversion center to the other side.

 

Figure \(\PageIndex{24}\): The inversion center in the icosahedron (Attribution: symotter.org/gallery)

Let us now look for improper rotations. The improper rotational axes with the highest order are S₁₀ axes. They are located in the same position as the C₅ axes, and go through two opposite corners (Figure \(\PageIndex{25}\)).

Figure \(\PageIndex{25}\): The S₁₀ improper rotational axes in the icosahedral point group (Attribution: symotter.org/gallery)

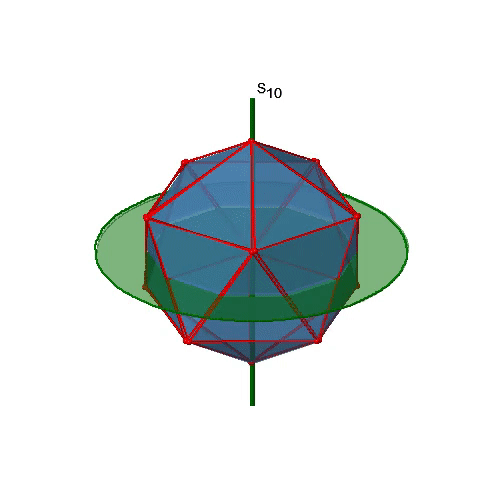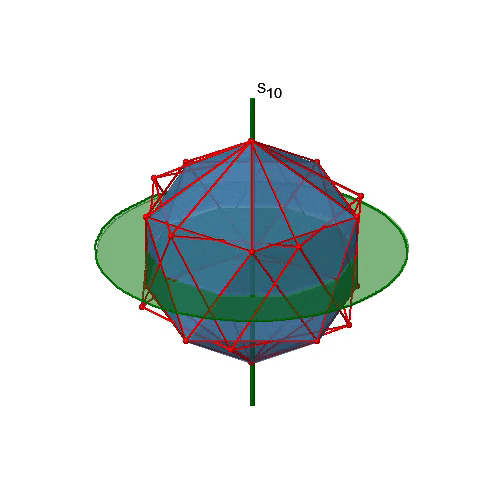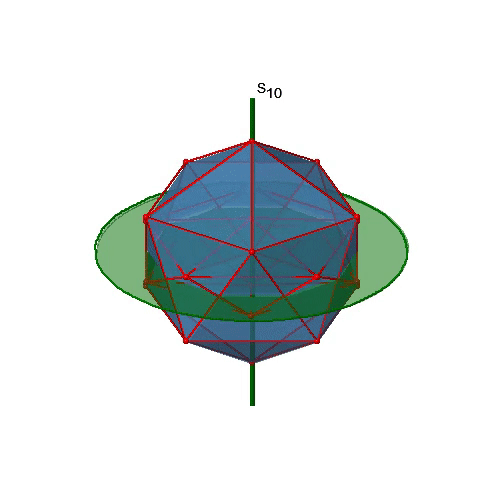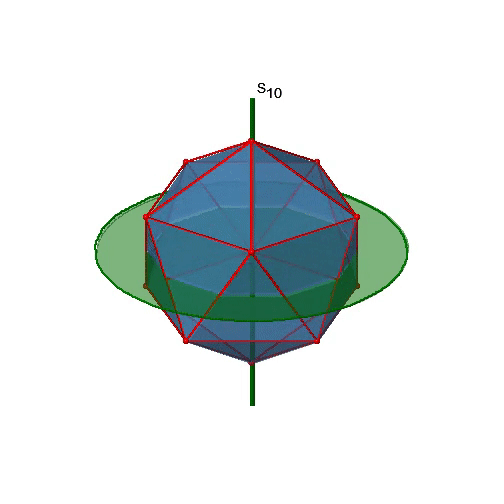
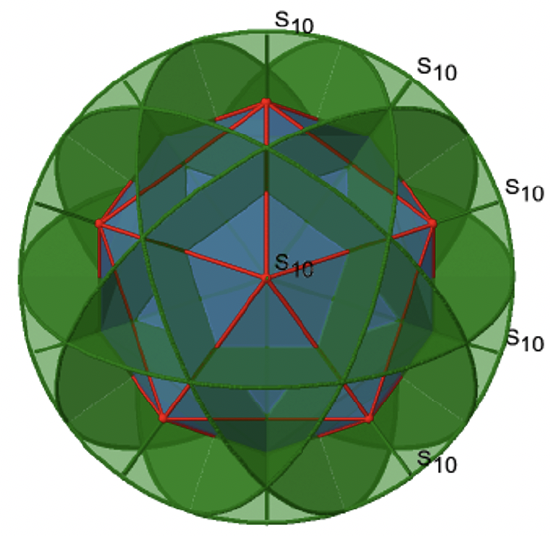
The S₁₀ exists because in an icosahedron there are pairs of co-planar pentagons that are oriented staggered relative to each other. The rotation around 36° brings one pentagon in eclipsed position relative to the other, but superposition is only achieved after the reflection at the mirror plane perpendicular to the rotational axis. Because one S₁₀ passes through two opposite vertices, and there are 12 vertices there are 6 S₁₀ improper axes. For each axis there are four unique symmetry operations, the S₁₀¹, the S₁₀³, the S₁₀⁷, and the S₁₀⁹. Therefore, there are overall 4x6=24 operations possible.

Figure \(\PageIndex{26}\): The S₆ rotation-reflections in the icosahedral point group (Attribution: symotter.org/gallery)

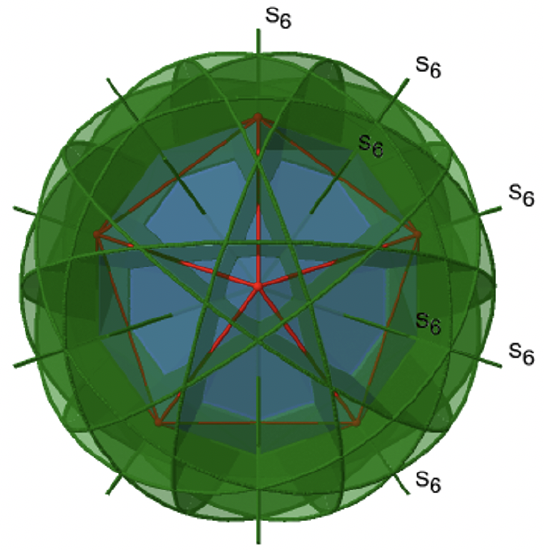
Are the lower order improper rotational axes? Yes, there are S₆ axes that pass through the centers of two opposite triangular faces (Figure \(\PageIndex{26}\)). This symmetry element exists because the two triangular faces are in staggered orientation to each other. Rotation alone brings one face in eclipsed orientation relative to the other, but reflection at a mirror plane perpendicular to the axis is required to achieve superposition. The S₆ axes are in the same location as the C₃ axes. There are 10 S₆ axes because there are twenty faces and one axis passes through two opposite faces. Only the S₆¹ and the S₆⁵ operations are unique S₆ operations, all others can be expressed by simpler operations. Therefore there are overall 10 S₆¹+10 S₆⁵ = 20 S₆ operations.

We have now found all symmetry operations for the I_h symmetry. There are overall 120 operations making the point group I_h the point group with the highest symmetry.

Symmetry Operations in the I_h Point Group

Every molecule or object in the I_h point group has the following 120 symmetry operations:

• E, 24 C₅, 20 C₃, 15 C₂, i, 24 S₁₀, 20 S₆, and 15 σ

Rotational Point Groups

After having discussed high and low symmetry point groups, let us next look at rotational point groups. Unlike the high symmetry point groups, these only have a single proper rotational axis. The presence or absence of reflection planes further defines this class of point groups

C_n Point Groups

In the most simple case the point groups do not have any additional symmetry element such as mirror planes or improper rotations. These point groups are called pure rotation groups and denoted C_n whereby n is the order of the proper rotation axis. An example is the hydrogen peroxide molecule H₂O₂ (Figure \(\PageIndex{27}\)). It has a so-called roof-structure due to its non-planarity. One hydrogen atom points toward us, and the other points away from us. This structure is due to the two electron-lone pairs at each sp³-hybridized oxygen atom. These electron-lone pairs consume somewhat more space than the H atoms, and there is electrostatic repulsion between the electron lone pairs. Therefore, the electron lone pairs at the different oxygen atoms try to achieve the greatest distance from each other. This forces the H-atoms out of the plane, leading to the roof-structure of the hydrogen peroxide. Because the H₂O₂ molecule is not planar, it only has a single C₂ axis, but no other symmetry element besides the identity. The C₂ axis passes through the center of the O-O bond. Execution of the C₂ operation swaps up both the O and the H atoms.

Figure \(\PageIndex{27}\): The C₂ rotational axis of hydrogen peroxide (Attribution: symotter.org/gallery)

C_nv Point Groups

Another class of groups are the pyramidal groups, denoted C_nv. They have n vertical mirror planes containing the principal axis C_n in addition to the principal axis C_n. Generally molecules belonging to pyramidal groups are derived from an n-gonal pyramid. An n-gonal pyramid has an n-gonal polygon as the basis which is capped. For example a trigonal pyramid has a triangular basis which is capped, a tetragonal pyramid has a square which is capped, and so on. The proper axis associated with a specific pyramid has the order n and goes through the tip of the pyramid and the center of the polygon. An example of a molecule with a trigonal pyramidal shape is the NH₃ (Figure \(\PageIndex{28}\)).

Figure \(\PageIndex{28}\): C₃ axis and vertical mirror planes in NH₃ (Attribution: symotter.org/gallery)

The three H atoms form the triangular basis of the pyramid, which is capped by the N atom. The NH₃ molecule belongs to the point group C_3v. The C₃ axis goes though the N atom which is the tip of the pyramid, and the center of the triangle defined by the H atoms. There are three vertical mirror planes that contain the C₃ axis. Each of them goes through an N-H bond.

C_nh Point Groups

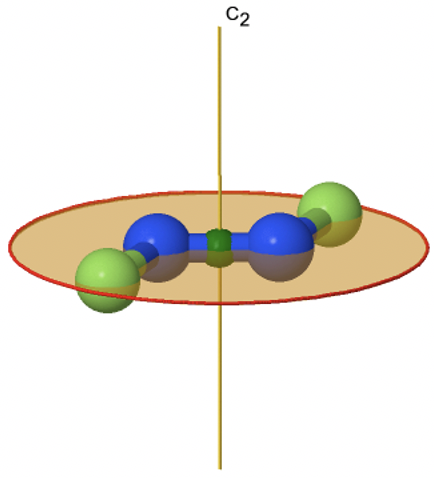
If we add a horizontal mirror plane instead of n vertical mirror planes to a proper rotational axis C_n we arrive at the point group type C_nh. The presence of the horizontal mirror planes also generates an improper axis of the order n. This is because when one can rotate and reflect perpendicular to the rotational axes independently, then it must also be possible to do it in combination. An example of a molecule belong to a C_nh group is the trans-difluorodiazene N₂F₂ (Figure \(\PageIndex{29}\)). It is a planar molecule with a C₂ axis going through the middle of the N-N double bond, and standing perpendicular to the plane of the molecule. The horizontal mirror plane stands perpendicular to the C₂ axis, and is within the plane of the molecule. There is an additional inversion center because an S₂ must exist which is the same as an inversion center. The inversion center is in the middle of the N-N bonds. Overall, the molecule has the symmetry C_2h.

Figure \(\PageIndex{29}\): C₂ axis and horizontal mirror plane in trans-N₂F₂ (Attribution: symotter.org/gallery)

S_2n Point Groups

The category of rotational point groups to be discussed are the improper rotation point groups. The only have one proper rotational axis, and an improper rotational axis that has twice the order of the proper rotational axis (Figure \(\PageIndex{30}\)). There may be an inversion center present depending on the order of the proper and improper axes. Molecules that fall into these point groups are rare. An example the tetramethylcycloocta-tetraene molecule (Figure \(\PageIndex{30}\)).

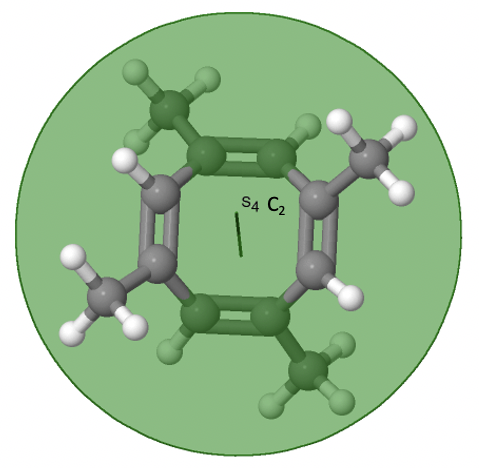
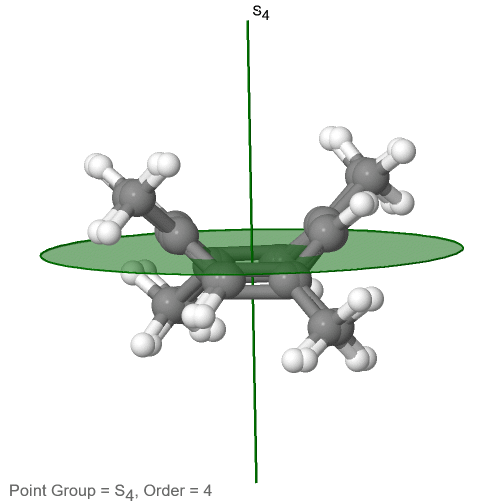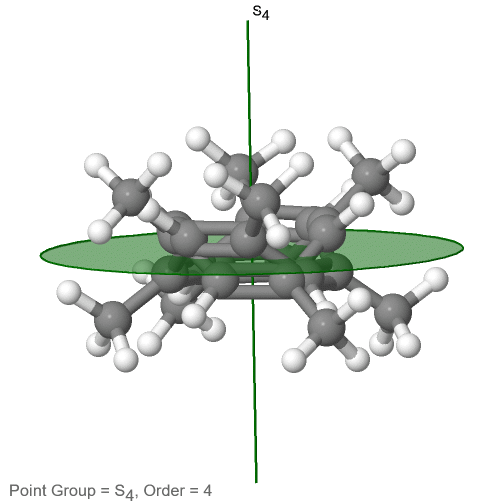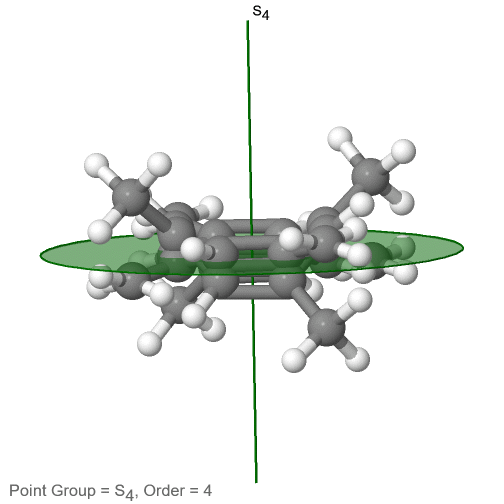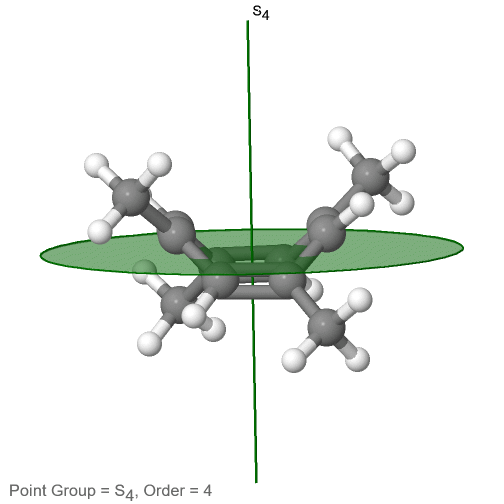
Figure \(\PageIndex{30}\): The S₄ and an C₂ axes of tetramethyl cycloocta-tetraene

It has an S₄ and an C₂ axis as the only symmetry elements besides the identity. Rotating by 90° alone does not superimpose the molecule because two C-C double bonds lie above the plane and two below the plane. In addition, two opposite methyl groups lie above and below the plane respectively. Therefore it needs the additional reflection to achieve superposition. There is also a C₂ axis which is in the same locations as the S₄ axis.

Dihedral Groups

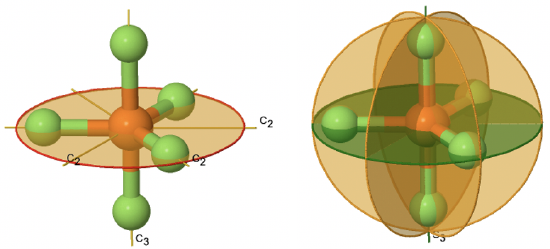
D_n Point Groups

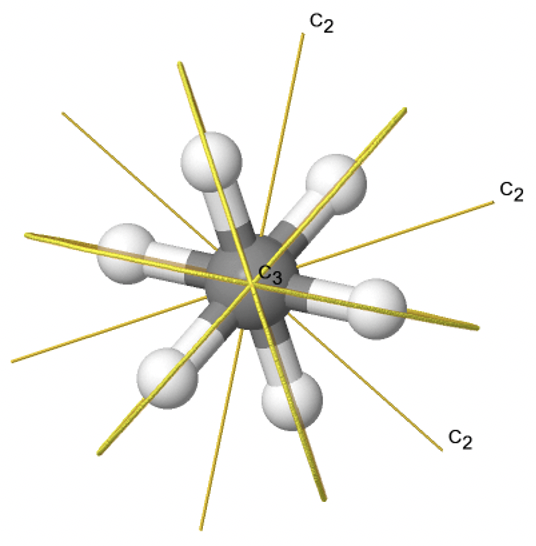
Dihedral groups are point groups that have n additional C₂ axes that stand perpendicular to the principal axis of the order n. If there are no other symmetry elements, then the point group is of the type D_n. For example in the point group D₃ there is a C₃ principal axis, and three additional C₂ axes, but no other symmetry element (Fig. 2.2.75). The tris-oxolatoferrate(III) ion belongs to this point group (Figure \(\PageIndex{31}\)). You can see that the C₃ axis stands perpendicular to the paper plane, and there are three C₂ axes in the paper plane.

 

Figure \(\PageIndex{31}\): The tris-oxolatoferrate(III) ion and its symmetry elements. (Attribution: symotter.org/gallery)

D_nh Point Groups

If a horizontal mirror plane is added to the C_n axis and the n C₂ axes we arrive at the D_nh point groups. The addition of the horizontal mirror plane generates further symmetry elements namely an S_n and n vertical mirror planes. An example for a molecule belonging to this class of point group is PF₅ (Figure \(\PageIndex{32}\)). It has a trigonal bipyramidal shape. The C₃ axis goes through the axial F atoms of the molecule, and the three C₂ axes go through the three equatorial F atom. The horizontal mirror plane stands perpendicular to the principal C₃ axis and is located within the equatorial plane of the molecule. In addition, there are the vertical mirror planes that contain the C₃ axis, and go through the three equatorial P-F bonds. There is also an S₃ axis which superimposes the C₃ axis.

Figure \(\PageIndex{32}\): The PF₅ molecule belonging to the point group D_3h and its symmetry elements. (Attribution: symotter.org/gallery)

D_nd Point Groups

If we add n vertical mirror planes to the principal axis and the n C₂ axes, we arrive at the point group D_nd. The vertical mirror planes are dihedral mirror planes because they bisect the angle between the C₂ axes. An example is the ethane molecule in staggered conformation which has the symmetry D_3d (Figure \(\PageIndex{33}\):). The C₃ axis goes along the C-C bond, and the 3C₂ axes pass through the middle of the carbon-carbon bond, and bisect the angle between two hydrogens and one carbon atom. The three dihedral mirror planes pass through the C-H bonds. In addition, the ethane molecule has an S₆ axis, and an inversion center.

Figure \(\PageIndex{33}\): The ethane molecule in the staggered conformation belongs to the point group type D_nd (Attribution: symotter.org/gallery)

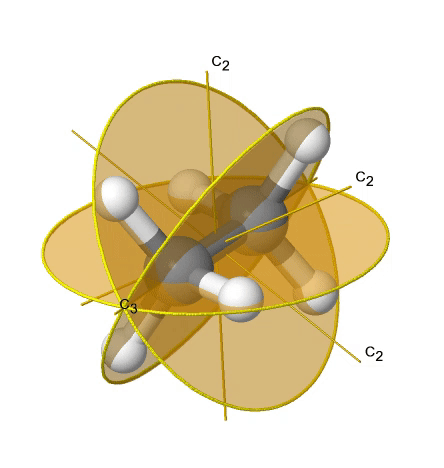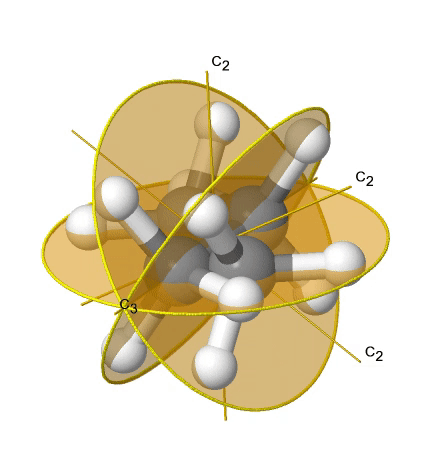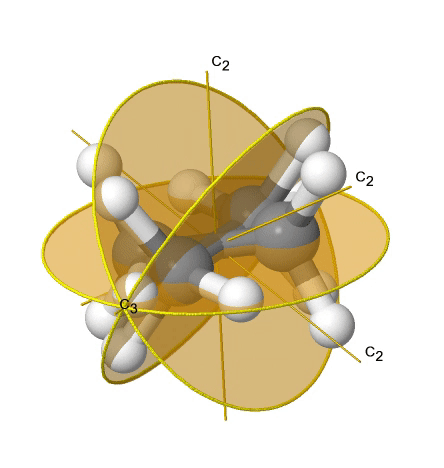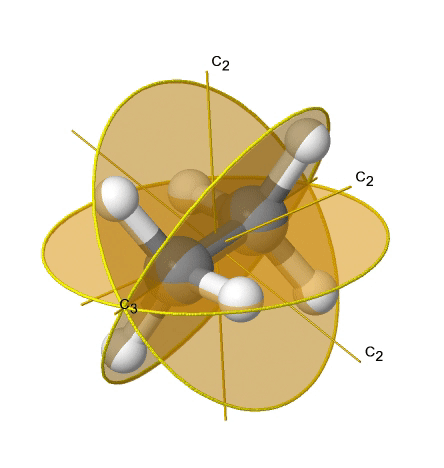
Linear Point Groups

The principal rotation axis in a linear molecule is a C_∞ axis, meaning the molecule can be rotated along its bond axis an infinitely small amount and remain unchanged. Linear molecules can be subdivided based on the presence or absence of a horizontal reflection plane and inversion center.

C_∞v point groups

A special n-gonal polygon is the cone. A cone can be conceived as an n-gonal pyramid with an infinite number n of corners at the base (Figure \(\PageIndex{34}\)).

Figure \(\PageIndex{34}\): Cone having a proper rotational axis with infinite order.

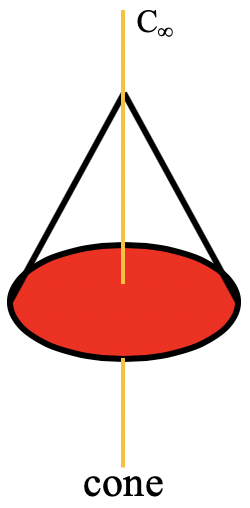
In this case the order of the rotational axis that passes through the tip of the cone and the center of the circular basis is infinite. This also means that there is an infinite number of vertical mirror planes that contain the C_∞ axis. The point group describing the symmetry of a cone is called the linear point group C_∞v. Polar, linear molecules such as CO, HF, N₂O, and HCN belong to this point group. You can see the HCN molecule with its C_∞ axis and its infinite number of vertical mirror planes below (Figure \(\PageIndex{35}\)). The infinite number of mirror planes, shown in blue are forming a cylinder that surround the molecule.

Figure \(\PageIndex{35}\): C_∞ axis of the HCN molecule.

D_∞h point groups

A special case of a D_nh group is the linear group D_∞h. An object that has this symmetry is a cylinder. A cylinder can be conceived as a prism with an infinite number of vertices. Thus, the principal axis that passes through a cylinder has infinite order. Because of the infinite order of the principal axis, there is an infinite number of C₂ axes that stand perpendicular to the principal axis. You can see one such C₂ going though the cylinder (Figure \(\PageIndex{36}\):).

Figure \(\PageIndex{36}\): Cylinder as an example of linear group D_∞h.

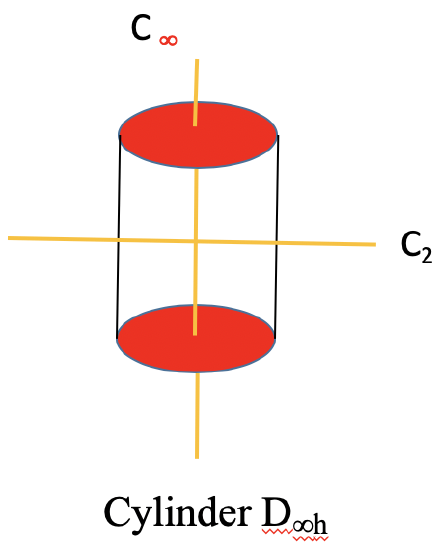
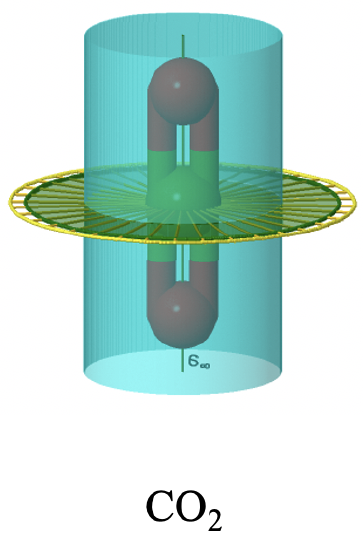
There is now also an improper axis of infinite order, as well as an infinite number of vertical mirror planes. Non-polar linear molecules like H₂, CO₂, and acetylene C₂H₂ belong to the point group D_∞h. You can see the C_∞ axis passing through a CO₂ molecule below (Figure \(\PageIndex{37}\)). You can see the infinite number of vertical mirror planes as a blue cylinder. The infinite number of C₂ axes is shown a yellow lines going around the molecule.

Figure \(\PageIndex{37}\): C_∞ in a CO₂ molecule.

Guide for the Determination of Point Groups

The symmetry operations a molecule possesses will determine which point group the molecule is in. The key to success is that you are able to see the symmetry elements in the molecule which takes practice. Luckily, especially for high symmetry point groups, you don't need to identify every single symmetry operation to correctly assign a point group. You can use a flow chart to identify a point group more easily. These flow charts ask systematic questions about the presence or absence of key symmetry elements. Eventually, after having answered enough questions the guide will lead you to the respective point group. You can see an example flow chart below (Figure \(\PageIndex{38}\):).

Figure \(\PageIndex{38}\): Flow chart for the determination of point groups. (CC BY-NC-SA; Catherine McCusker)

You can first ask if the molecule is linear (has a C_∞ rotation axis). Then we can ask next, if there is a high symmetry point group. This is the case when there are either 4C₃, 3C₄, or 6C₅ rotational axes present, standing for tetrahedral, octahedral, and icosahedral symmetry, respectively. If there is are no C_n axes of any type present the molecule must be in a low symmetry point group. We ask if there are n ⟂C₂ axes in addition to the C_n principal axis. If this is so, then we must have a dihedral group of the D type. If there are no ⟂ C₂ axes in addition to the C_n, the group must be a rotational (C) group.

Example: Dibromonaphtalene

Let us practice the point group flow chart by example. Let us look at the dibromonaphtalene molecule (Figure \(\PageIndex{39}\)).

Figure \(\PageIndex{39}\): Guide for determining the point group of dibromonaphtalene

After determining that the molecule is not linear or in a high symmetry group (having 2 or more C₃ rotation axes), the first question we ask is: Can you see at least one proper rotational axis? The answer is yes. There is a C₂ proper rotational axis that stands perpendicular to the plane of the molecule and goes through the center of the C-C bond that is shared by the two aromatic rings. Next we can think about if the there are 2C₂ axes in addition to the C₂ axes we already found. The answer is no, so the point group cannot be a dihedral (D) group. Next, we would ask: Is there a horizontal mirror plane. This is indeed the case. There is a horizontal mirror plane in the plane of the molecule. It does not move any atoms around, but as we discussed before, a mirror does not need to do this to exist. This identifies the point group as C_2h.

The Symmetry Challenge at Otterbein University is a great way to practice assigning molecules to point groups!

Exercise \(\PageIndex{1}\)

Use the flow chart to assign the point group for (a) BH₃ and (b) H₂O.

Answer

(a) BH₃ has a trigonal planar geometry.

• It has a C₃ principal rotation axis
• It doesn't have C₅, C₄, or multiple C₃ axes
• It has 3 ⟂ C₂ axes
• It has a σ_h (the plane of the molecule)
• The point group is D_3h

(b) H₂O has a bent geometry.

• It has a C₂ principal rotation axis
• It doesn't have any C₅, C₄, or C₃ axes
• It doesn't have ⟂ C₂ axes
• It doesn't have a σ_h reflection plane
• It does have 2 σ_v reflection planes
• The point group is C_2v

---

Dr. Kai Landskron (Lehigh University). If you like this textbook, please consider to make a donation to support the author's research at Lehigh University: Click Here to Donate.