1: Introducing Measurements in the Laboratory (Experiment)
- Page ID
- 221123
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objectives
- To use a metric ruler to measure the dimensions of regular geometric shapes, and to use these measurements to determine the areas of the shapes.
- To measure the volume of a sample of water using a graduated cylinder and a beaker in order to compare their precision.
- To measure the mass of an item using a triple-beam balance and an analytical (electronic) balance in order to compare their precision; also, to determine the mass of a powder by weighing by difference.
- To measure the melting point of an unknown solid and identify it using this measured value.
Our knowledge of chemistry and chemical processes largely depends on our ability to obtain correct information about matter. Often this information is quantitative, in the form of measurements. In this lab, students will be introduced to some common measuring instruments so that they can practice making measurements, and to learn about instrument precision. In Part A of this lab, a metric ruler will be used to measure length in centimeters (cm). In Part B, a beaker and a graduated cylinder will be used to measure liquid volume in milliliters (mL). In Part C, an electronic balance and a triple-beam balance will be to measure mass in grams (g). In Part D, a thermometer will be used to measure temperature in degrees Celsius (°C).
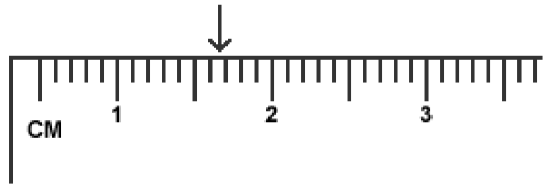
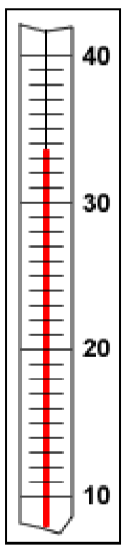
Since all measuring devices are subject to some error, it is impossible to make exact measurements. Scientists record all the digits of a measurement that are known exactly, plus the first one that is uncertain. These digits are collectively referred to as significant digits. Digital instruments, such as an electronic balance, are designed to limit themselves to the correct number of significant digits, and their readings are properly recorded as given. However, when using analog instruments such as rulers and thermometers, the experimentalist is responsible for determining the correct number of significant figures. These instruments are properly read to one place beyond the graduations of the scale.
Example \(\PageIndex{2}\): Measuring the Volume of a Liquid
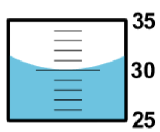
When measuring liquid volumes, the graduated scale must be read from the lowest point of the curved surface of the liquid – the liquid meniscus.
The graduated cylinder markings are every 1-milliliter. The correct reading is 30.0 mL. The first 2 digits 30.0 are known exactly. The last digit 30.0 is uncertain. Even though it is a zero, it is significant and must be recorded.
Note that the measuring devices used in this lab may have different scale graduations than the ones shown in these examples. Thus, be sure to make it a regular habit to check the scales on all equipment.
When making measurements, it is important to be as accurate and precise as possible. Accuracy is a measure of how close an experimental measurement is to the true, accepted value. Precision refers to the degree of uncertainty in a measurement. For example, a mass measurement of 48.26 g has an uncertainty of ±0.01 g, while a measurement of 48.3 g has an uncertainty of ±0.1 g. Since the measurement of 48.26 g has less uncertainty, it is the more precise measurement. In general, the more decimal places provided by a device, the more precise the measurement will be.
Since measurements are often used in calculations to obtain other values of interest, it is important to consider the number of significant figures that should be recorded for the results of such calculations. If multiplying or dividing measured values, the result should be reported with the lowest number of significant figures used in the calculation. If adding or subtracting measured values, the result should be reported with the lowest number of decimal places used in the calculation.
Example \(\PageIndex{4}\): Significant Figures in calculated values
(a) A student runs 18.752 meters in 54.2 seconds. Calculate his average velocity (or speed).
\[velocity = \frac{distance}{time}\]
\[= \frac{18.752 m}{54.2 s}\]
\[= 0.345978 m/s \text{ from calculator}\]
\[= 0.346 m/s \text{ to 3 significant figures}\]
(b) The mass of a glass is measured to be 12.466 grams. If 10.33 grams of water are added to this glass, what is the total combined mass?
\[\text{total mass} = 12.466 g + 10.33 g\]
\[= 22.796 g \text{ from calculator}\]
\[= 22.80 g \text{ to 2 decimal places}\]
The temperature that will be measured in this lab is the melting point of an unknown solid. Melting point is a physical property. When a solid is heated continuously, a point will eventually be reached where it undergoes a physical change and becomes a liquid. The temperature at which liquid first appears is defined as the melting point of that substance. Since all pure substances have unique melting points, a measured melting point can be used to identify an unknown substance by comparing it with a list of known substances and their accepted, true melting points.
The accuracy of a measured value, such as a melting point, may be evaluated by a calculation of percent error. Percent error is a common way of reporting how close a measured experimental value (\(EV\)) is to the true value (\(TV\)):
\[\text{Percent Error} = \frac{| EV − TV |}{TV} \times 100\]
Accurate measurements will typically have low percent errors of <5%.
Procedure
Materials and Equipment
Metric ruler*, shape sheet, electronic balance, large test tube, 100-mL beaker, 100-mL graduated cylinder, triple-beam balance, 250-mL Erlenmeyer flask, electronic balance, sugar, Bunsen burner, thermometer, 400-mL beaker, stand and ring clamp, small watch glass, wire gauze, capillary tube, latex tubing, scoopula and unknown solids.
Safety
In Part D you will be heating a solid powder and several pieces of equipment with an open Bunsen burner flame. Exercise extra caution while using the Bunsen burner, and please remember that the heated items will be very hot to the touch.
Part A: Measuring the Dimensions of Regular Geometric Shapes
- Check out a ruler from the stockroom.
- Obtain a “shape sheet” from your instructor, and then use the ruler to measure the dimensions of the two geometric shapes on it. Measure the length and width of the rectangle, and the diameter of the circle. Record these measurements on your report form.
- When finished, return the ruler to the stockroom.
- Use your measurements to calculate the areas of the assigned geometrical shapes.
\[\text{Area of a rectangle}=l \times w\]
\[\text{Area of a circle} = 2 \pi r\]
(where \(r = \text{radius} = \frac{1}{2} \text{ the diameter}\))
Part B: Measuring the Volume of a Sample of Water
- Obtain a large test tube from your instructor. Fill this test-tube to the brim with tap water, then carefully transfer it to a 100-mL beaker (obtain from your locker). Note that if your 100-mL beaker has no scale markings on it, you will need to take it to the stockroom and swap it for one that does. Measure and record the volume of water in the beaker.
- Again, fill the same test-tube to the brim with tap water, then carefully transfer it to a 100-mL graduated cylinder (obtain from your locker). Measure and record the volume of water in the graduated cylinder. Do these measured volumes have the same number of significant figures?
Part C: Measuring the Mass of Solids
Comparing the Precision of two types of Balances
- Use a triple-beam balance to obtain the mass of a 250-mL Erlenmeyer flask (obtain from your locker).
- Now use an electronic balance to obtain the mass of the same Erlenmeyer flask. Do these measured masses have the same number of significant figures? Be sure to record your measured masses on your report form.
Weighing by Difference
- Using the electronic balance again, obtain the mass of a 100-mL beaker. If you already used this same beaker in Part B, make sure that you carefully dry it before weighing it.
- Add two spoonfuls of sugar to this beaker, using your scoopula. Do not do this over the balance! Then obtain the new combined mass of both the beaker and the sugar. Be sure to use the same electronic balance as before.
- When finished, dispose of the sugar used in the sink.
- Use your two measurements to determine the mass of sugar (only) weighed out.
Part D: Measuring the Melting Point of an Unknown Solid
- Record the ID code of the unknown solid assigned to you and your partner. Powdered samples of the unknown solids are located at the front of lab on the instructor’s lab bench.
- Obtain a capillary tube from your instructor. Press the open end of the capillary tube into the powder. Then turn the tube over and tap the tube lightly against the lab bench to allow the powder to fall into the sealed end. Repeat until you have a depth of about 2-mm of solid in the tube.
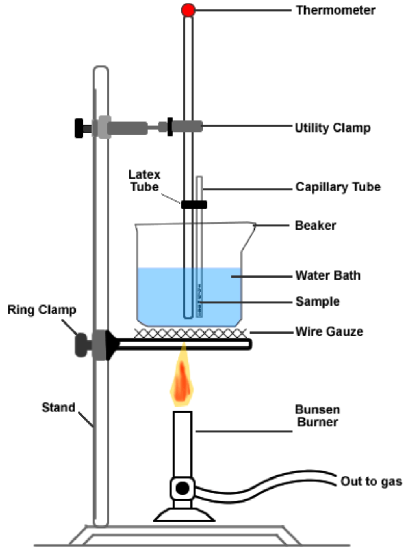
- Assemble your equipment as shown in the diagram on page 5.
- Use a large 400-mL beaker half-filled with tap water for the hot water bath.
- Use a small piece of latex tubing like a rubber band to attach the capillary tube to your thermometer. The sealed end should be close to the bulb of the thermometer.
- Place a slotted stopper around the thermometer, and using a clamp, suspend it in the water bath.
- Heat the water bath slowly with your Bunsen burner. The flame should be adjusted to a moderate temperature, with its tip touching the bottom of the beaker. Stir the bath continuously and watch your sample carefully.
- The melting point is the temperature at which liquid first appears. Record your melting point.
- Share your measured value with all other groups who were assigned the same unknown solid as you. You will also need to obtain and record the melting points that they have measured.
- Your unknown solid is one of the substances listed in the table below. Identify your solid by comparing your experimental melting point with the true melting points supplied. Then evaluate the accuracy in your measurement by calculating your percent error.
|
Substance |
Melting Point (in °C)* |
|---|---|
|
L-Menthol |
41.6 |
|
Benzophenone |
48.2 |
|
Myristic Acid |
54.0 |
|
Palmitic Acid |
62.0 |
|
Stearic Acid |
68.0 |
|
Vanillin |
82.1 |
* This melting point data was obtained from the NIST Standard Reference Database Number 69 (http://webbook.nist.gov/chemistry/). Please note that organic solids actually melt over a range of temperatures. The melting points given in the table represent the lowest temperature in that range, where liquid formation is first observed. Also note that melting points depend on the purity of the solid.
- The unknown sample and the capillary tube (together) should be disposed of in the labeled waste container provided when you are finished.
Pre-laboratory Assignment: Introducing Measurements in the Laboratory
- In Part A of this lab, you will measure the dimensions (length, width, diameter) of several geometric shapes.
- Using a ruler, you measure the length of a rectangle to be 12.75 cm and the width to be 3.64 cm. Calculate the area of this rectangle (show work), reporting your answer to the correct number of significant figures.
- What is the formula for the area of a circle?
- In Part B of this lab, you will measure the volume of a sample of water, in milliliters (mL).
- What two measuring instruments will you use to measure the water volume?
- Consider the following two volume measurements: 57.7 mL and 57.68 mL. Which of these is the more precise measurement, and why?
- In Part C of this lab, you will measure the mass of several different items, in grams (g).
- What are the two types of balances you will use to measure mass?
- An empty beaker has a measured mass of 29.456 g. When some salt is added to the beaker, the combined mass is 36.176 grams. Calculate the mass of the salt only (show work), reporting your answer to the correct number of significant figures.
- In Part D of this lab, you will measure the melting point of an unknown solid, in degrees Celsius (°C).
- Define “melting point".
- Is melting point a physical or chemical property of matter?
- A student measures the melting point of an unknown compound to be 53.5 °C. She later discovers that the compound is chlorothymol, with a true melting point of 58.8 °C. Calculate her percent error (show work) to the correct number of significant figures. The required formula is on page 3 of the Procedure document.
- You will use a variety of equipment to measure the melting point of the solid. Sketch a set-up of the equipment on the back of this page, and label all items in your sketch.
Lab Report: Introducing Measurements in the Laboratory
Part A: Measuring the Dimensions of Regular Geometric Shapes
Experimental Data
|
Shape |
Dimensions |
Measurement |
# Significant Figures |
|---|---|---|---|
|
Rectangle |
Length |
||
|
Width |
|||
|
Circle |
Diameter |
Data Analysis
- Perform the conversions indicated below. Show your work, and report your answers in scientific notation.
- Convert the measured rectangle length to pm.
- Convert the measured circle diameter to km.
- Calculate the areas of your rectangle and circle in cm2. Show your work, and report your answers to the correct number of significant figures.
- Area of rectangle
- Area of circle
- Convert the area of your circle to μm2. Show your work, and report your answer in scientific notation.
Part B: Measuring the Volume of a Sample of Water
Experimental Data
|
Measuring Device |
Volume Measurement |
# Significant Figures |
|---|---|---|
|
100-mL Beaker |
||
|
100-mL Graduated Cylinder |
Data Analysis
- Compare your volume measurements in the table above. Which instrument, the beaker or the graduated cylinder, provides the more precise measurement? Explain.
- Convert the volume of water obtained using the graduated cylinder to hm3. Show your work, and report your answer in scientific notation.
Part C: Measuring the Mass of Solids
Experimental Data
Table 1 – Mass of an Erlenmeyer Flask
|
Measuring Device |
Mass Measurement |
# Significant Figures |
|---|---|---|
|
Triple-Beam Balance |
||
|
Electronic Balance |
Table 2 – Weighing by Difference
|
Mass Measurement |
# Significant Figures |
|
|---|---|---|
|
Mass of Empty Beaker |
||
|
Mass of Beaker + Sugar |
Data Analysis
- Compare your mass measurements obtained for the Erlenmeyer flask in Table 1. Which balance, triple-beam or electronic, provides the more precise measurement? Explain.
- Consider the data you obtained in Table 2.
- Calculate the mass of sugar weighed out. Show your work.
- Circle one: When performing the above calculation, significant figures / decimal places are the primary consideration.
- Perform the conversions indicated below. Show your work, and report your answers in scientific notation.
- Convert the mass of the sugar weighed out to fg.
- Convert the mass of the sugar weighed out to Gg.
Part D: Measuring the Melting Point of an Unknown Solid
Experimental Data
Unknown Compound ID Code:
|
Measured by |
Melting Point |
# Significant Figures |
|---|---|---|
|
Group 1: You and your partner |
||
|
Group 2 |
||
|
Group 3 |
||
|
Group 4 |
||
|
Average Value |
Data Analysis
- Using the average value above, identify your unknown compound (see Procedure, Part D, #7).
- Name of Compound:
- True Melting Point:
- Which of the measured melting points recorded in the table was the most accurate? Explain.
- Calculate the percent error between the experimental melting point that you and your partner measured and the substance’s true melting point. Report your answer to the correct number of significant figures.
- Perform the temperature conversions indicated below. Show your work, and report your answers to the correct number of significant figures.
- Convert the true melting point of your compound to K.
- Convert the true melting point of your compound to °F.