Simple Buffer Demonstration
- Page ID
- 221987
Chemical Concepts Demonstrated
- Properties of buffers and buffer solutions
Demonstration
| 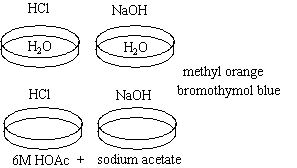 |
Observations
The water turns red with one drop of HCl and blue with one drop of NaOH.
Large amounts of HCl are added to the buffer solution and the color do es not change. Large amounts of NaOH are added in another buffer solution and the color still does not change. It should be noted that this will not go on forever.
es not change. Large amounts of NaOH are added in another buffer solution and the color still does not change. It should be noted that this will not go on forever.
Explanations
Buffers lessen or absorb the drastic changes in pH that occur when small amounts of acids and bases are added to solution. In this case, the buffer solution is made of water, acetic acid and sodium acetate. The acetate ions shift the equilibrium, depressing the ionization of the acetic acid. The pH will remain essentially constant as long as the ratio of the concentrations of acids and bases are more or less constant. When enough acid or base is added to exceed the buffer capacity of the solution, the pH will change significantly and its color will change.
OAc - (aq) + H3O+(aq) ----> HOAc (aq) + H2O (l) (addition of acid)
HOAc (aq) + OH - (aq) ----> OAc - (aq) + H2O (l) (addition of base)
Contributors
- Dr. George Bodner (Perdue University)

